- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
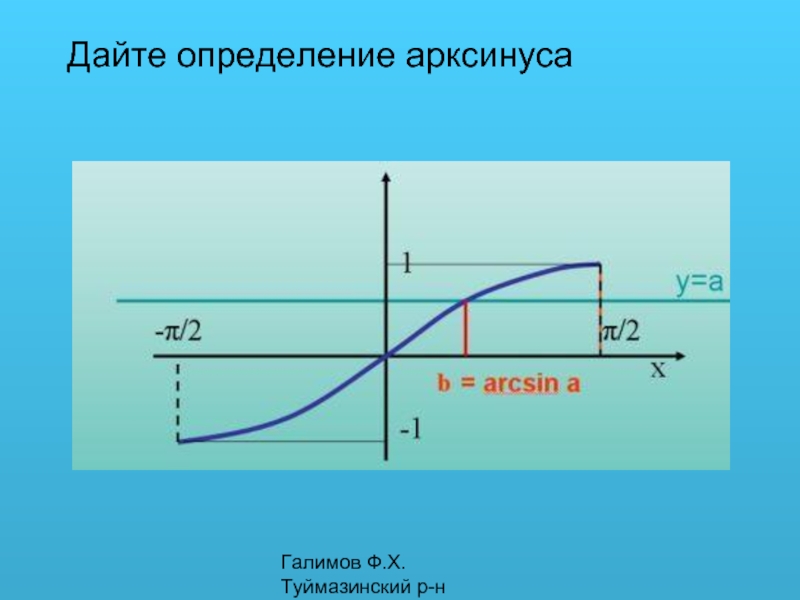
Дайте определение арксинуса презентация
Содержание
- 1. Дайте определение арксинуса
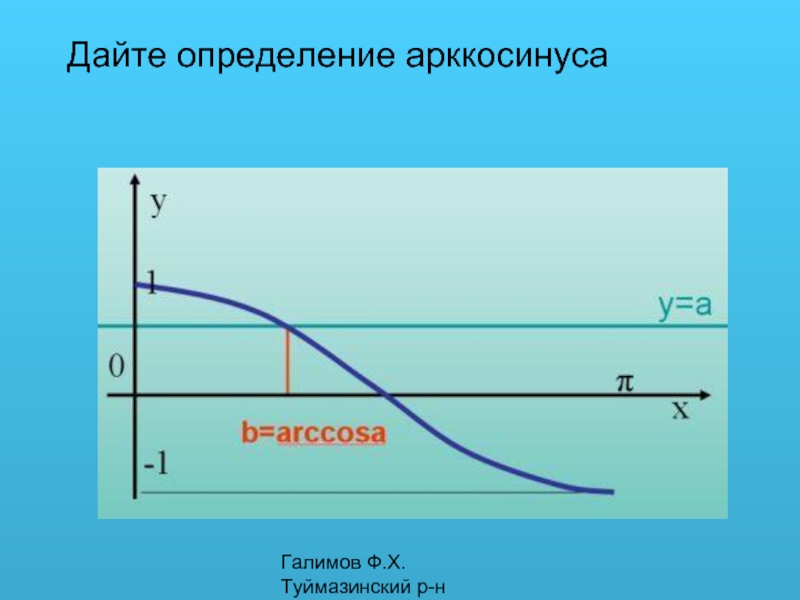
- 2. Галимов Ф.Х. Туймазинский р-н Дайте определение арккосинуса
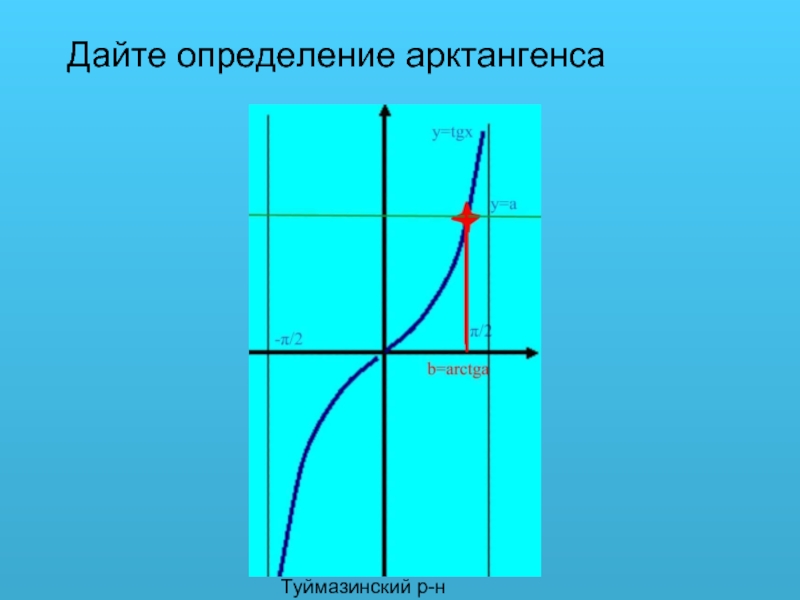
- 3. Галимов Ф.Х. Туймазинский р-н Дайте определение арктангенса
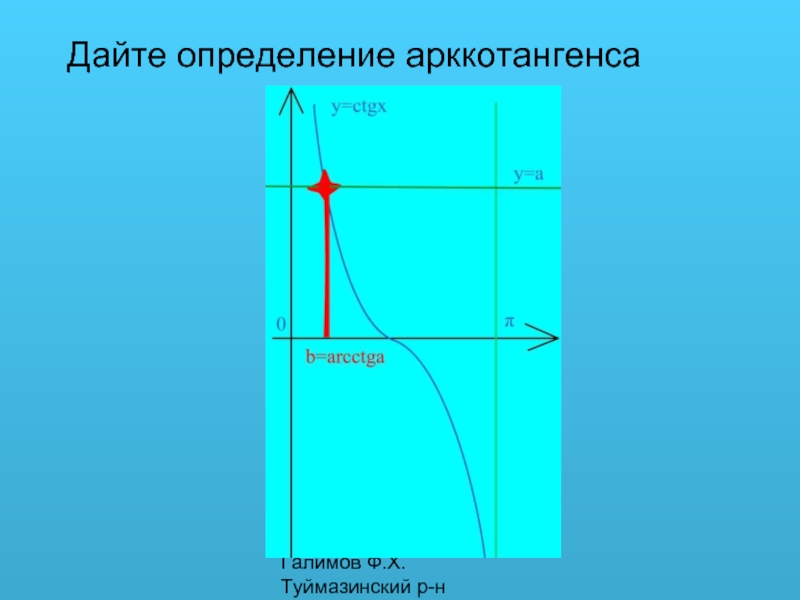
- 4. Галимов Ф.Х. Туймазинский р-н Дайте определение арккотангенса
- 5. Галимов Ф.Х. Туймазинский р-н π/4 -π/4 π/3 -π/3 0 не существует
- 6. Галимов Ф.Х. Туймазинский р-н π/4 3π/4 π/6 5π/6 не существует π/2
- 7. Галимов Ф.Х. Туймазинский р-н -π/6 π/6 5π/6 π/4 π/3 3π/4 π/4 -π/4 π/6 -π/3
- 8. Галимов Ф.Х. Туймазинский р-н Имеют ли смысл выражения? Почему?
- 9. Галимов Ф.Х. Туймазинский р-н Новая тема. Решение простейших тригонометрических уравнений
- 10. Галимов Ф.Х. Туймазинский р-н 1. Уравнение cos
- 11. Галимов Ф.Х. Туймазинский р-н y=a y=a При
- 12. Галимов Ф.Х. Туймазинский р-н y=1 Рассмотрим
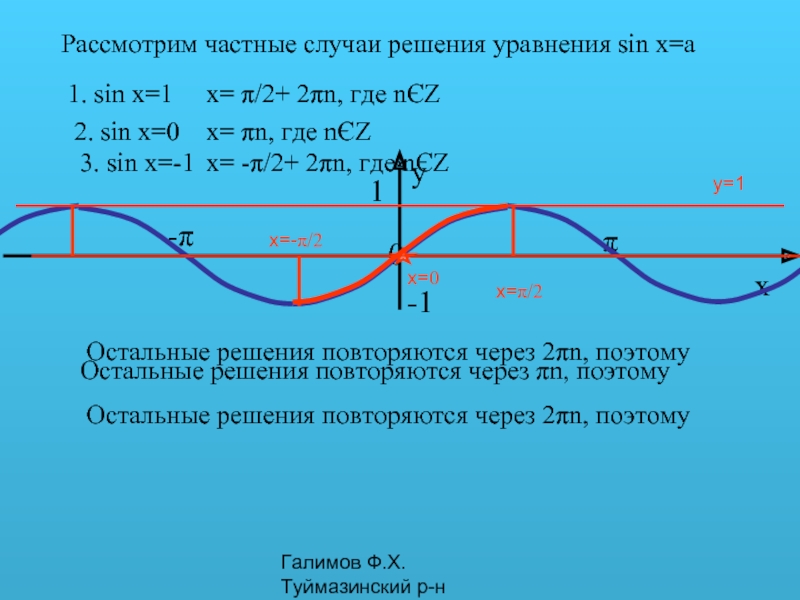
- 13. Галимов Ф.Х. Туймазинский р-н 1. Уравнение sin
- 14. Галимов Ф.Х. Туймазинский р-н y=a При aЄ[-1;1]
- 15. Галимов Ф.Х. Туймазинский р-н Получаем две группы
- 16. Галимов Ф.Х. Туймазинский р-н y=1 Рассмотрим
- 17. Галимов Ф.Х. Туймазинский р-н Решите уравнения
- 18. Галимов Ф.Х. Туймазинский р-н
- 19. Галимов Ф.Х. Туймазинский р-н
- 20. Галимов Ф.Х. Туймазинский р-н
- 21. Галимов Ф.Х. Туймазинский р-н
- 22. Галимов Ф.Х. Туймазинский р-н
- 23. Галимов Ф.Х. Туймазинский р-н С решением уравнении
Слайд 10Галимов Ф.Х. Туймазинский р-н
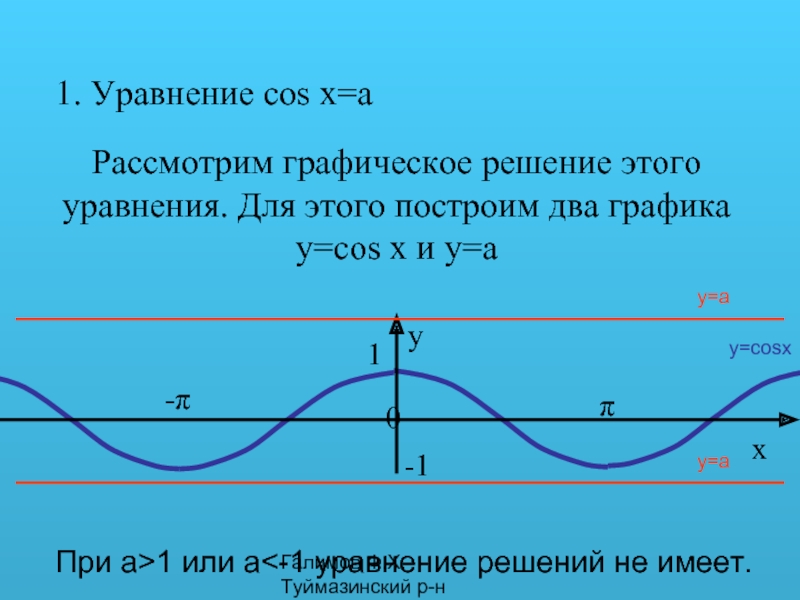
1. Уравнение cos x=a
Рассмотрим графическое решение этого уравнения.
y=cosx
y=a
При а>1 или a<-1 уравнение решений не имеет.
y=a
Слайд 11Галимов Ф.Х. Туймазинский р-н
y=a
y=a
При aЄ[-1;1] уравнение cos x=a имеет бесконечное множество
Мы можем записать одно из решений для х Є[0; π].
x1=arccos a
Другие решения выразим через это решение.
x2=-arccos a
x3=arccos a-2π
-2π
+2π
x4=-arccos a+2π
Функция y=cos x имеет период 2π, поэтому остальные решения отличаются от х1 и х2 на 2πn, где nЄZ.
Таким образом все решения уравнения cos x=a записываются в виде
x=±arccos a+2πn, nЄZ
Слайд 12Галимов Ф.Х. Туймазинский р-н
y=1
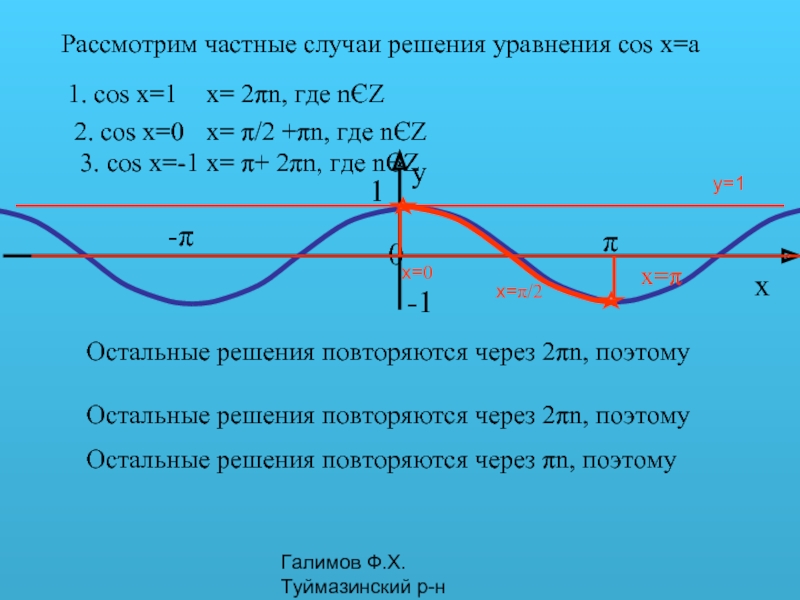
Рассмотрим частные случаи решения уравнения cos x=a
1. cos
x=π/2
Остальные решения повторяются через 2πn, поэтому
x= 2πn, где nЄZ
2. cos x=0
x=0
Остальные решения повторяются через πn, поэтому
x= π/2 +πn, где nЄZ
3. cos x=-1
Остальные решения повторяются через 2πn, поэтому
x= π+ 2πn, где nЄZ
x=π
Слайд 13Галимов Ф.Х. Туймазинский р-н
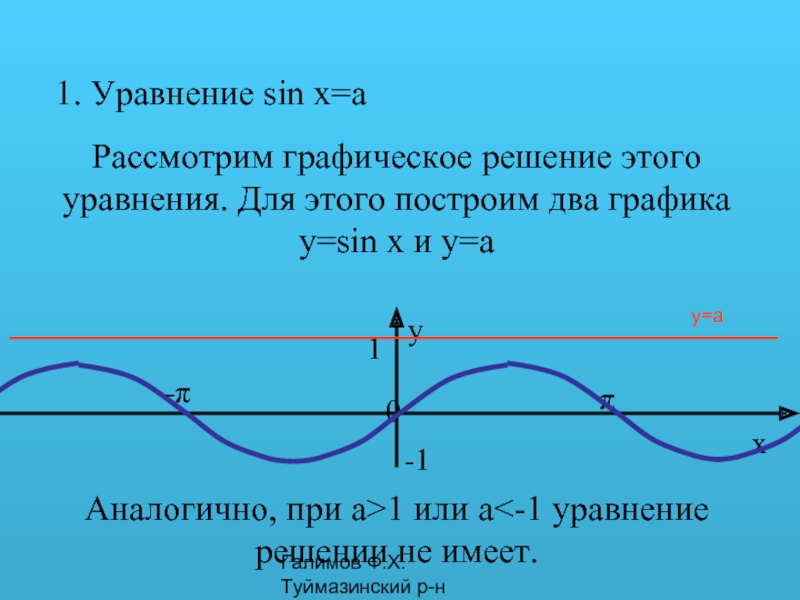
1. Уравнение sin x=a
Рассмотрим графическое решение этого уравнения.
y=a
Аналогично, при a>1 или a<-1 уравнение решении не имеет.
Слайд 14Галимов Ф.Х. Туймазинский р-н
y=a
При aЄ[-1;1] уравнение sin x=a имеет бесконечное множество
Мы можем записать одно из решений для х Є[- π/2; π/2].
x1=arcsin a
Другие решения выразим через это решение.
x2=π-arcsin a
Так-как функция y=sin x имеет период 2π, остальные решения отличаются от этих двух на 2πn, где nЄZ.
Получаем две группы решении
x1=arcsin a+ 2πn,
x2= π -arcsin a+ 2πn, где nЄZ,
Слайд 15Галимов Ф.Х. Туймазинский р-н
Получаем две группы решении
x1=arcsin a+ 2πn,
x2= π
Эти две группы можно записать одной формулой
x=(-1)n arcsin a+ πn, где nЄZ
Слайд 16Галимов Ф.Х. Туймазинский р-н
y=1
Рассмотрим частные случаи решения уравнения sin x=a
1. sin
x=π/2
Остальные решения повторяются через 2πn, поэтому
x= π/2+ 2πn, где nЄZ
2. sin x=0
x=0
Остальные решения повторяются через πn, поэтому
x= πn, где nЄZ
3. sin x=-1
Остальные решения повторяются через 2πn, поэтому
x= -π/2+ 2πn, где nЄZ
x=-π/2
Слайд 23Галимов Ф.Х. Туймазинский р-н
С решением уравнении tg x=a и ctg x=a
Д/р:п.9,
№136(в,г),
№137(в,г),
№138(в,г),
№139(в,г).
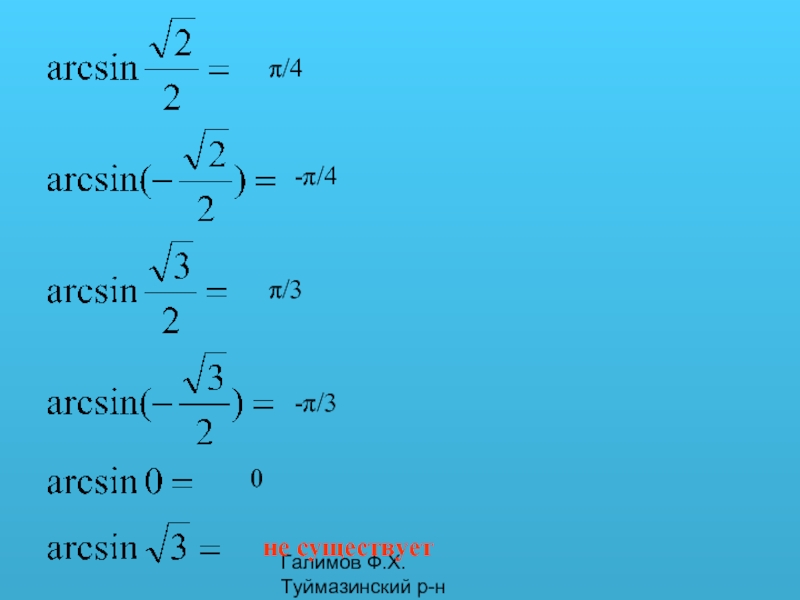
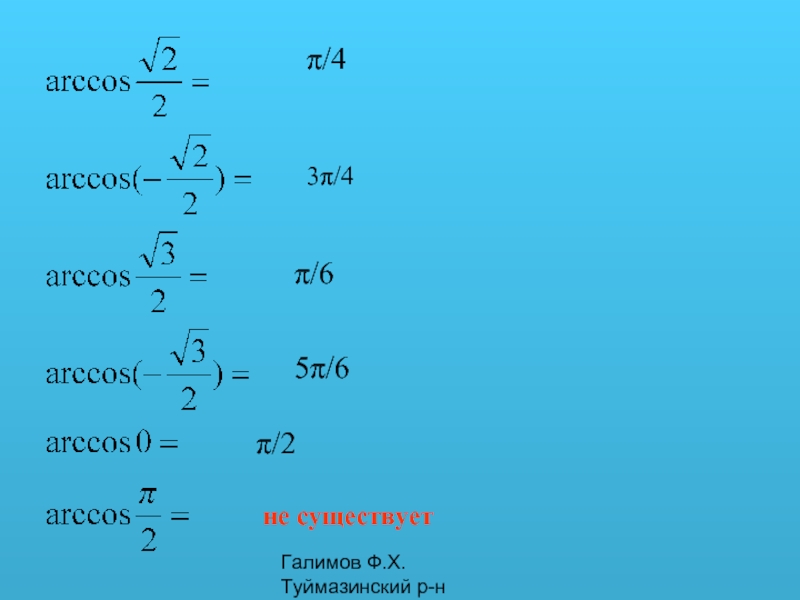



![Галимов Ф.Х. Туймазинский р-нy=ay=aПри aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений.Мы можем записать одно](/img/tmb/1/53152/9ed0779b1185e7254bd426463a6612fb-800x.jpg)
![Галимов Ф.Х. Туймазинский р-нy=aПри aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений.Мы можем записать одно](/img/tmb/1/53152/fad328fcd0ff4d676a8f4258a257ec8d-800x.jpg)