N.V. Khotkevych*, Yu.A. Kolesnichenko*,
J.M. van Ruitenbeek**
*Физико-технический институт низких температур
им. Б.И.Веркина НАН
**Kamerlingh Onnes Laboratorium, Universiteit Leiden
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Conductance of a STM contact on the surface of a thin film презентация
Содержание
- 1. Conductance of a STM contact on the surface of a thin film
- 2. Сканирующий туннельный микроскоп (СТМ) СТМ позволяет получать
- 3. Физические основы СТМ и СТС Туннельный ток
- 4. Топографическое STM изображение островков Pb, выращенных на
- 5. Квантовый размерный эффект и СTM Honbin et
- 6. Цель работы: найти вольт - амперную характеристику
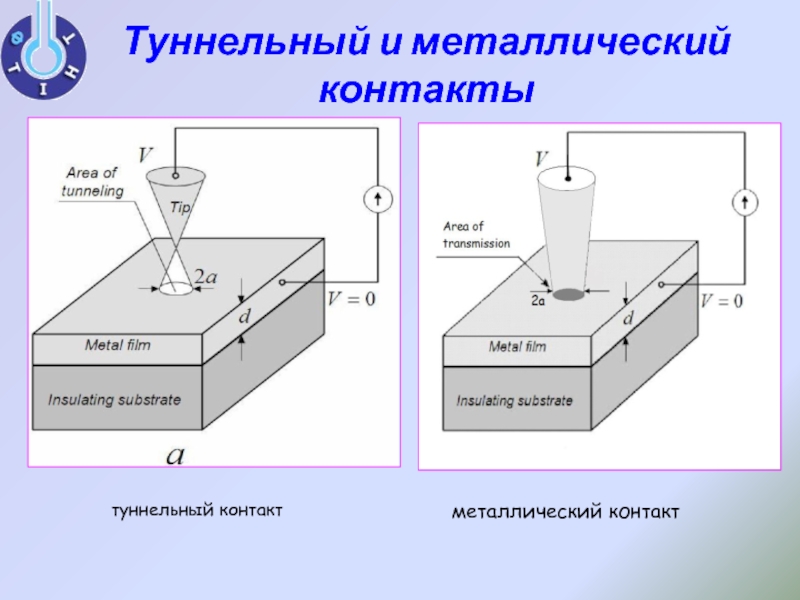
- 7. Туннельный и металлический контакты металлический контакт туннельный контакт
- 8. Вольт-амперная характеристика и кондактанс контакта Полный ток
- 9. Модель и основные уравнения Туннельный контакт Кулик, Омельянчук, Мицай, ЖЭТФ, 1974
- 10. Решение уравнения Шредингера (туннельный контакт) Граничные условия
- 11. Волновая функция прошедших электронов Квадрат модуля волновой функции для прошедших в пленку электронов
- 12. Модель и основные уравнения (металлический контакт) Ицкович, Шехтер, ФНТ, 1985
- 13. Волновая функция прошедших электронов
- 14. Дифференциальная проводимость G=dI/dV при V=0 и
- 15. Дифференциальная проводимость G(V)=dI/dV при T=0 Туннельный режим Контактный режим
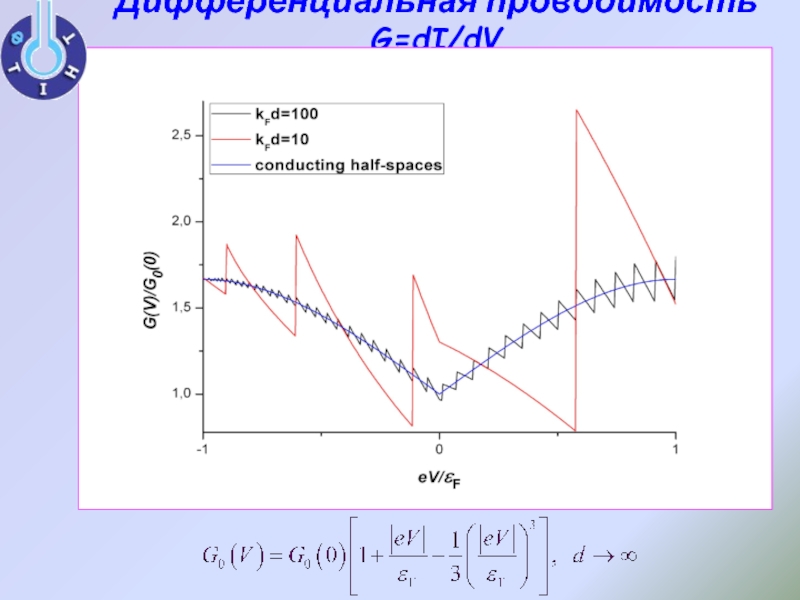
- 16. Дифференциальная проводимость G=dI/dV
- 17. eV>0 -> туннелирование в пленку
- 18. При eV
- 19. Заключение Теоретически исследована дифференциальная проводимость контакта, радиус
- 20. Спасибо за внимание
Сканирующий туннельный микроскоп (СТМ) СТМ позволяет получать изображение проводящей поверхности в масштабе 0.1 нм Изображение атомов Cr на поверхности Fe (001)
Слайд 1Conductance of a STM contact on the surface of a thin
film
Слайд 2Сканирующий туннельный микроскоп (СТМ)
СТМ позволяет получать изображение
проводящей поверхности в масштабе 0.1
нм
Изображение атомов Cr на
поверхности Fe (001)
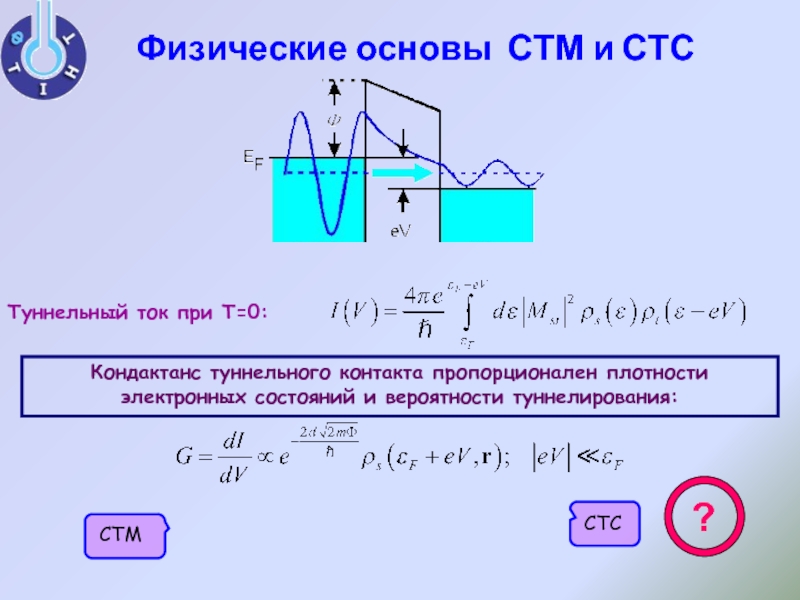
Слайд 3Физические основы СТМ и СТС
Туннельный ток при Т=0:
Кондактанс туннельного контакта
пропорционален плотности электронных состояний и вероятности туннелирования:
Слайд 4Топографическое STM изображение островков Pb, выращенных на подложке Si(111)
Германиевые нанонити, выращенные
на кремниевой подложке
Использование STM для изучения объектов
малого размера
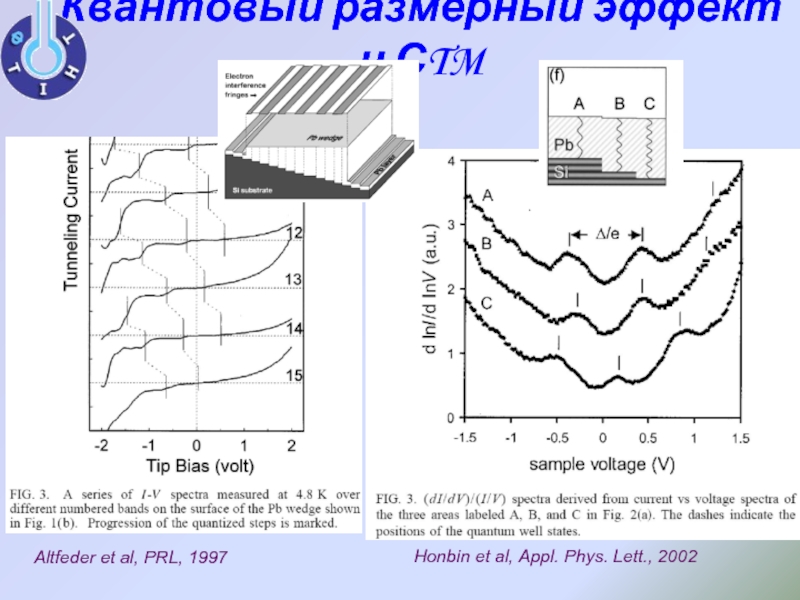
Слайд 5Квантовый размерный эффект и СTM
Honbin et al, Appl. Phys. Lett., 2002
Altfeder
et al, PRL, 1997
Слайд 6Цель работы: найти вольт - амперную характеристику точеного контакта между массивным
проводником и квантовой пленкой
Два направления в теории СТМ
Численные расчеты, учитывающие кристаллическую
структуру
образца и контакта
Приближение свободных электронов
Слайд 8Вольт-амперная характеристика и кондактанс контакта
Полный ток через контакт
Плотность потока прошедших контакт
электронов
Дифференциальный кондактанс
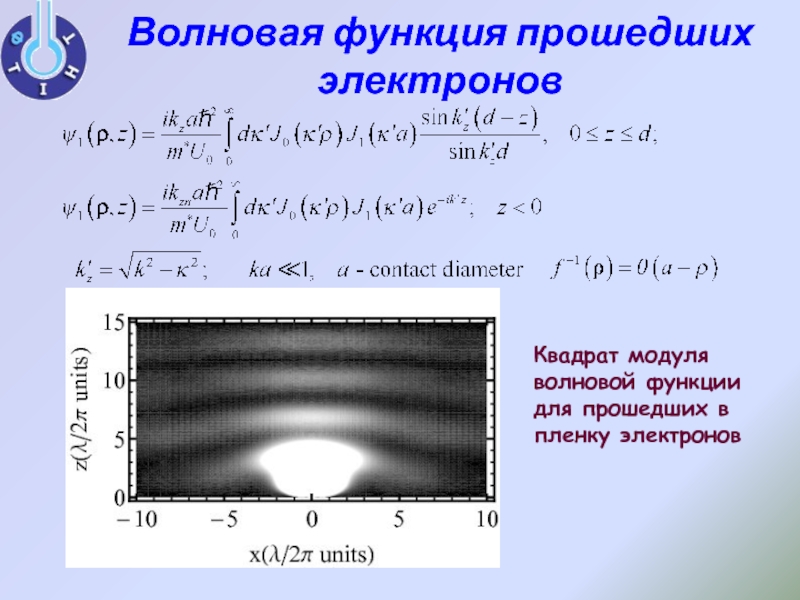
Слайд 11Волновая функция прошедших электронов
Квадрат модуля волновой функции
для прошедших в пленку
электронов
Слайд 14Дифференциальная проводимость
G=dI/dV при V=0 и T=0
плотность состояний
в изолированной пленке
число
уровней размерного квантования под поверхностью Ферми
Слайд 17 eV>0 -> туннелирование в пленку
Если
то электрон может туннелировать
в любую из подзон.
При становится возможным
тунеллирование в NF +1 – ю
подзону размерного квантования.
При становится возможным
тунеллирование в NF +1 – ю
подзону размерного квантования.
Зависимость дифференциальной проводимости
от напряжения
G(V) испытывает положительный скачок. Такие скачки повторяются при увеличении eV для следующих уровней размерного квантования, лежащих выше.
Слайд 18При eV
уровней под поверхностью Ферми.
Зависимость дифференциальной проводимости от напряжения
Слайд 19Заключение
Теоретически исследована дифференциальная проводимость контакта, радиус которого намного меньше фермиевской длины
волны, расположенного на поверхности квантовой пленки.
Рассмотрены контакт с потенциальным барьером малой прозрачности, и контакт без барьера.
В рамках модели получены выражения для туннельного тока и дифференциальной проводимости такой системы.
Кондактанс контакта не пропорционален плотности состояний изолированной пленки. Результат не зависит от амплитуды барьера в плоскости контакта и определяется «микроконтактной природой» сопротивления.
Расстояние между соседними скачками G(V) по шкале напряжения равно расстоянию между соседними энергетическими уровнями размерного квантования. Зависимость G(V) для различных знаков напряжения позволяет изучать уровни как ниже, так и выше уровня Ферми.
Рассмотрены контакт с потенциальным барьером малой прозрачности, и контакт без барьера.
В рамках модели получены выражения для туннельного тока и дифференциальной проводимости такой системы.
Кондактанс контакта не пропорционален плотности состояний изолированной пленки. Результат не зависит от амплитуды барьера в плоскости контакта и определяется «микроконтактной природой» сопротивления.
Расстояние между соседними скачками G(V) по шкале напряжения равно расстоянию между соседними энергетическими уровнями размерного квантования. Зависимость G(V) для различных знаков напряжения позволяет изучать уровни как ниже, так и выше уровня Ферми.
