Алгоритмы управления мобильным LEGO-роботом. Движение по линии презентация

Содержание

План занятия Релейный двухпозиционный регулятор П-регулятор – движение по линии ПД-регулятор – движение по линии Кубическая составляющая Плавающий коэффициент Интегральная составляющая

Слайд 1Алгоритмы управления мобильным LEGO-роботом. Движение по линии
Сергей Александрович Филиппов,
Санкт-Петербургский Физико-математический

лицей №239

Слайд 2План занятия
Релейный двухпозиционный регулятор
П-регулятор – движение по линии
ПД-регулятор – движение по

линии
Кубическая составляющая
Плавающий коэффициент
Интегральная составляющая

Слайд 3Подключение датчика
Меню Robot -> Motors and Sensors Setup -> Sensors
#pragma config(Sensor,

S1, , sensorLightActive)

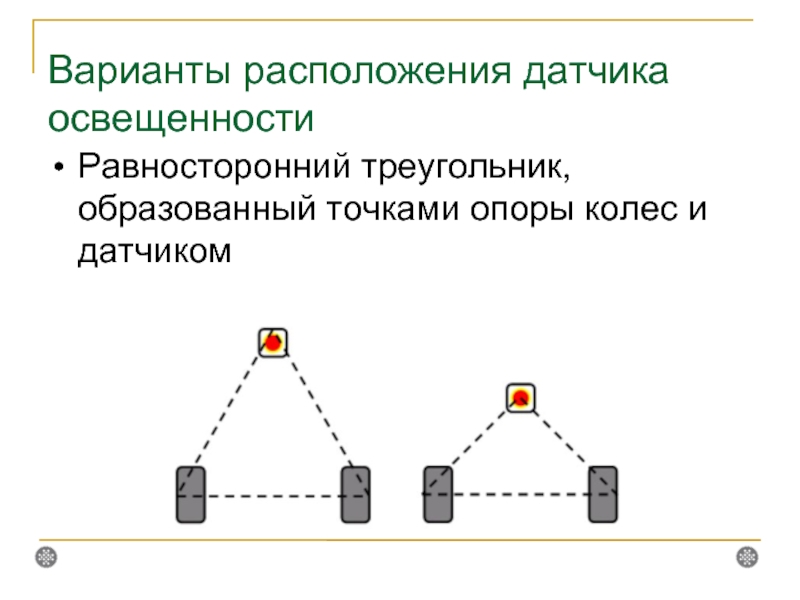
Слайд 4Варианты расположения датчика освещенности
Равносторонний треугольник, образованный точками опоры колес и датчиком

Слайд 5Релейный регулятор: движение вдоль границы черного и белого
int grey=45;
while (true)

// grey - значение серого
{
if (SensorValue[S1]>grey){
motor[MotorB]=100;
motor[MotorC]=0;
}
else{
motor[MotorB]=0;
motor[MotorC]=100;
}
wait1Msec(1);
}

Поиск значения серого: View - > Light Sensor (active) - > Port 1

Слайд 6Пропорциональный регулятор
В задачах автоматического регулирования управляющее воздействие u(t) обычно является функцией

динамической ошибки – отклонения e(t) регулируемой величины x(t) от ее заданного значения x0(t):
e(t)=x0(t)-x(t)

Пропорциональный регулятор – это устройство, оказывающее управляющее воздействие на объект пропорционально его отклонению от заданного состояния.
u0(t)=ke
Здесь k – это коэффициент усиления регулятора.

Слайд 7Пропорциональный регулятор: движение по линии
Также как и в релейном регуляторе, необходимо

определить среднее значение grey между черным и белым. Это будет то состояние датчика освещенности s1, к которому должна стремиться система.

float k=2, v=50;
while(true)
{
u=k*(SensorValue[S1]-grey);
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}


Слайд 8Калибровка
Установить датчик на белое поле и включить робота
int white=SensorValue[S1];
PlaySound(soundBeepBeep);

Установить датчик на

черное поле и нажать кнопку
while(SensorValue[S2]==0); // Жди, пока не нажато
wait1Msec(100); // Защита от залипаний
while(SensorValue[S2]==1); // Жди, пока нажато
wait1Msec(100);
int black=SensorValue[S1];
PlaySound(soundBeepBeep);
int grey=(white+black)/2;

Установить робота на старт и нажать кнопку
while(SensorValue[S2]==0);
wait1Msec(100);
while(SensorValue[S2]==1);

Слайд 9Калибровка с выводом на экран
...
int grey=(white+black)/2;

Взять робота и посмотреть на экран

nxtDisplayBigTextLine(1,

“white=%d”, white);
nxtDisplayBigTextLine(3, “black=%d”, black);
nxtDisplayBigTextLine(5, “grey=%d”, grey);

Установить робота на старт и нажать кнопку

while(SensorValue[S2]==0);
wait1Msec(100);
while(SensorValue[S2]==1);

Слайд 10Калибровка с одной переменной
Установить датчик на белое поле и включить робота

int

grey=SensorValue[S1];
PlaySound(soundBeepBeep);

Установить датчик на черное поле и нажать кнопку

while(SensorValue[S2]==0); // Жди, пока не нажато
wait1Msec(100); // Защита от залипаний
while(SensorValue[S2]==1); // Жди, пока нажато
wait1Msec(100);
grey=(grey+SensorValue[S1])/2;
PlaySound(soundBeepBeep);

Установить робота на старт и нажать кнопку

while(SensorValue[S2]==0);
wait1Msec(100);
while(SensorValue[S2]==1);

Слайд 11Автоматическая круговая калибровка
Установить робота на линию на границу черного и белого

и включить

int white=SensorValue[S1];
int black=SensorValue[S1];
motor[motorB]=30;
motor[motorC]=-30;
nMotorEncoder[motorB]=0;

while(nMotorEncoder[motorB]<239*4) // Полный поворот на месте
{
if (SensorValue[S1]>white)
white=SensorValue[S1];
if (SensorValue[S1] black=SensorValue[S1];
wait1Msec(5);
}
motor[motorB]=0;
motor[motorC]=0;
grey=(white+black)/2;
PlaySound(soundBeepBeep);

Вывести результат на экран
Установить робота на старт и нажать кнопку

Слайд 12Калибровка в процессе движения
Установить робота на белое и включить

int white=SensorValue[S1];
int black=SensorValue[S1]-10;
int

grey=(white+black)/2;

while(true)
{
int Sv1=SensorValue[S1];
u=k*(Sv1-grey);
motor[motorB]=v+u;
motor[motorC]=v-u;
if (Sv1>white)
white=Sv1;
if (Sv1 black=Sv1;
grey=(white+black)/2;
wait1Msec(1);
}
Для отладки выводить результат калибровки на экран

Слайд 13И-регулятор: накопление ошибки
Накопление ошибки в интегральной составляющей

float i=0, ki=0.01;
while(true)
{
e=S1-grey;
i=i+ki*e;


u=i;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Слайд 14И-регулятор: управление с ограничением
Ограничение интегральной составляющей в пределах допустимого управляющего воздействия

float

i=0, ki=0.01, maxi=50;
while(true)
{
e=S1-grey;
i=i+ki*e;
if (abs(i)>maxi) i=sgn(i)*maxi;
u=i;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Слайд 15ПИ-регулятор с ограничением
Объединение интегральной и пропорциональной составляющей в пределах допустимого управляющего

воздействия

float i=0, kp=1, ki=0.01, maxi=50;
while(true)
{
e=S1-grey;
p=kp*e;
i=i+ki*e;
if (abs(i)>maxi) i=sgn(i)*maxi;
u=p+i;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Слайд 16Кубический регулятор
Рассчитывается отклонение
e=SensorValue[S1]-grey
Возводится в куб
uk=k2*(e*e*e), где k2≈0.01
Управляющее воздействие: пропорциональное+кубическое
upk = k1*e

+ k2*e*e*e

Коэффициент k2 при кубической составляющей должен быть такой, чтобы при максимальном отклонении получать величину, сравнимую с мощностью моторов (100). Коэффициент k1 может быть невелик.



up

uk




up

uk


Слайд 17Движение по границе черного и белого с кубическим регулятором
Резкие повороты обеспечиваются

кубическим регулятором. При малых отклонениях он не оказывает большого влияния

float k1=2, k2=0.03;
while(true)
{
e=SensorValue[S1]-grey;
u=k1*e + k2*e*e*e;
motor[motorB]=50+u;
motor[motorC]=50-u;
wait1Msec(1);
}

Слайд 18
Движение по границе черного и белого с помощью ПД-регулятора
ud=k*(S1-Sold)/Δt,
где S1

– текущие показания датчика, Sold – показания на предыдущем шаге.
Дифференциальная составляющая компенсирует пропорциональную
u = up+ud
u = k1*(S1-grey) + k2*(S1-Sold)

Можно показать, что для устойчивого достижения цели коэффициент k2 при дифференциальной составляющей должен превышать k1

S1

Sold


up

ud


Слайд 19ПД-регулятор: вариант записи
Использование ошибки в Д-составляющей

eold=0;
while(true)
{
e=SensorValue[S1]-grey;
u=k1*e + k2*(e-eold);
eold=e;


motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Слайд 20ПИД-регулятор
float ki=0.01, kp=1, kd=10, i=0, eold=0;
while(true)
{
e=SensorValue[S1]-grey;
p=kp*e;
i=i+ki*e;
if

(abs(i)>maxi) i=sgn(i)*maxi;
d=kd*(e-eold);
eold=e;
u=p+i+d;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

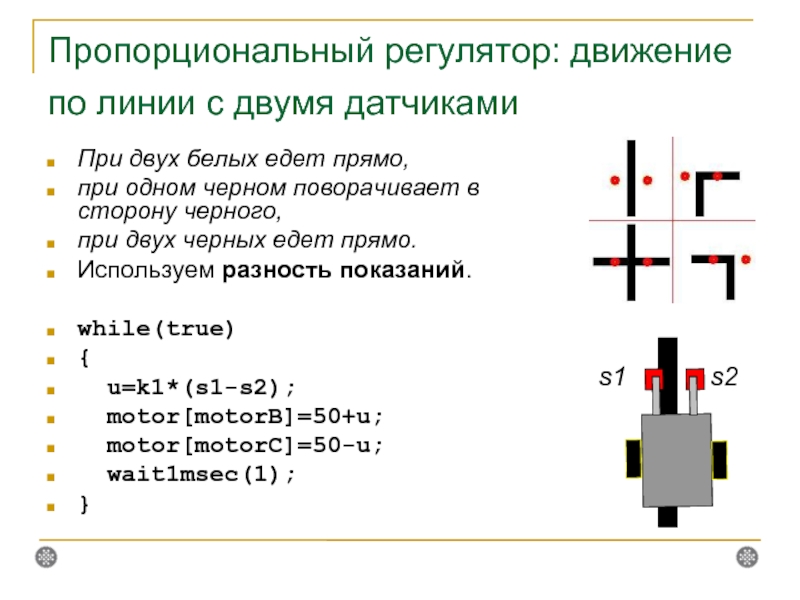
Слайд 21Пропорциональный регулятор: движение по линии с двумя датчиками
При двух белых

едет прямо,
при одном черном поворачивает в сторону черного,
при двух черных едет прямо.
Используем разность показаний.

while(true)
{
u=k1*(s1-s2);
motor[motorB]=50+u;
motor[motorC]=50-u;
wait1msec(1);
}


s1

s2

Слайд 22Пропорциональный регулятор: движение по линии с двумя датчиками
Датчики могут быть

откалиброваны по-разному
Рассчитывается разность отклонений
Начальные значения на одноцветной поверхности

left=s1;
right=s2;
while(true)
{
u=k1*((s1-left)-(s2-right));
motor[motorB]=50+u;
motor[motorC]=50-u;
wait1Msec(1);
}

Слайд 23Пропорциональный регулятор: устранение статической ошибки
Пусть статическая ошибка показывает разность показаний

датчиков на белом:
es = left – right
Динамическа ошибка e вычисляется в движении и компенсируется статической ошибкой

e = (sv1-left)-(sv2-right) = sv1 – sv2 – es

es=sv1-sv2;
while(true)
{
e=sv1-sv2-es;
u=k1*e;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Слайд 24
ПД-регулятор: движение по линии с двумя датчиками
Запоминаем отклонение в переменной

e, предыдущее – в переменной eold
Добавим контроль скорости на поворотах
v=100-abs(u)*0.2

es=SensorValue[s1]-SensorValue[s2];
eold=0;
while(true)
{
e=SensorValue[s1]-SensorValue[s2]-es;
u=k1*e+k2*(e-eold);
eold=e;
v=100-abs(u)*0.2;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1msec(1);
}

s1

s2

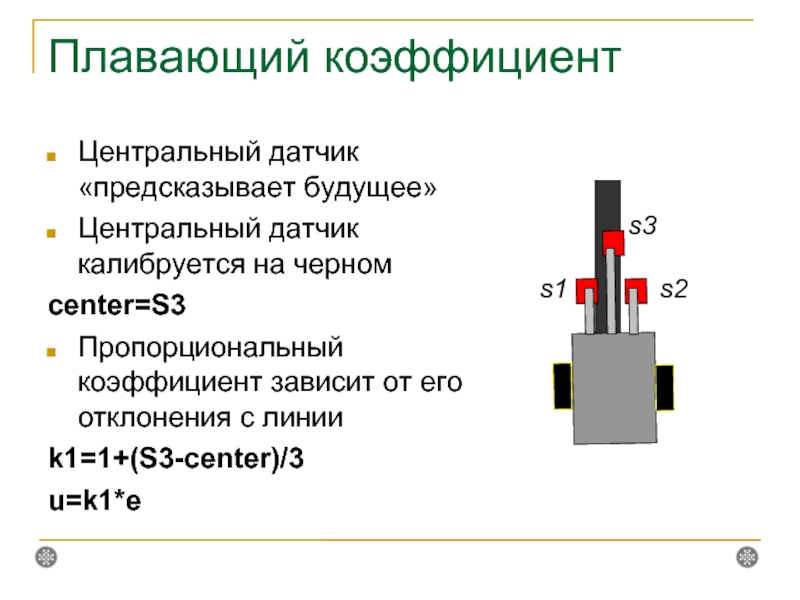
Слайд 25Плавающий коэффициент
Центральный датчик «предсказывает будущее»
Центральный датчик калибруется на черном
center=S3
Пропорциональный коэффициент зависит

от его отклонения с линии
k1=1+(S3-center)/3
u=k1*e




Слайд 26Плавающий коэффициент для пропорционального регулятора
Плавающий коэффициент можно применить к любому регулятору

left=s1;
right=s2;
center=s3;
while(true)
{

e=(s1-left)-(s2-right);
k1=1+(s3-center)/10;
u=k1*e;
Motor[MotorB]=50+u;
Motor[MotorC]=50-u;
wait1msec(1);
}

Слайд 27Инверсная линия
Предварительная калибровка двух датчиков
Движение на одном датчике на П- или

ПД-регуляторе
Второй датчик рядом с первым следит за цветом поля
Изменение знака управляющего воздействия (направления управления) в зависимости от показаний второго датчика.

Слайд 28Инверсная линия
while(true)
{
if (SensorValue[s2]>grey2)
r=1;
else
r=-1;
e=SensorValue[S1]-grey1;

u=r*(k*e);
motor[MotorB]=50+u;
motor[MotorC]=50-u;
wait1msec(1);
}

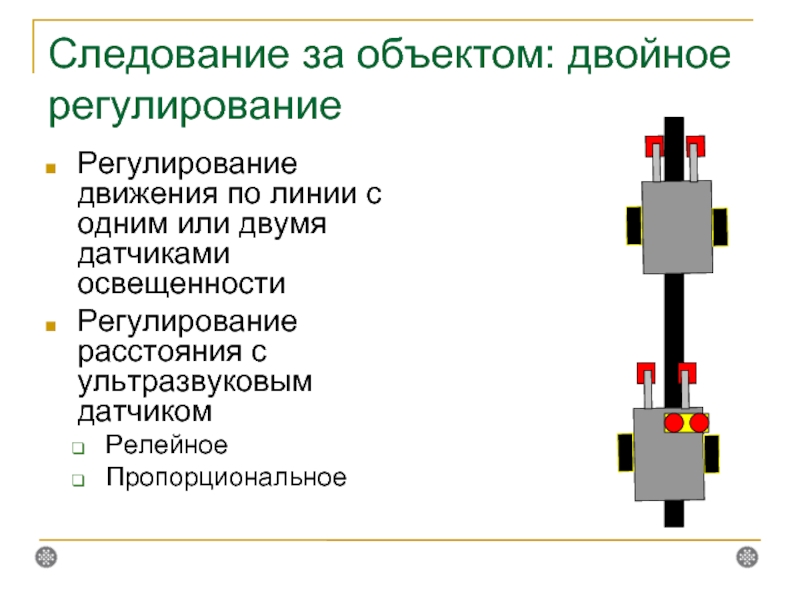
Слайд 29Следование за объектом: двойное регулирование









Регулирование движения по линии с одним или

двумя датчиками освещенности
Регулирование расстояния с ультразвуковым датчиком
Релейное
Пропорциональное

Слайд 30
Контроль расстояния с совмещением регуляторов по датчику ультразвука


// ПРОПОРЦИОНАЛЬНЫЙ
int e;
float v,

k=5;
while(true)
{
e=SensorValue[S3]-30;
v=e*k;
if (v>100) v=100;
motor[motorB]=v;
motor[motorC]=v;
wait1Msec(1);
}




// РЕЛЕЙНЫЙ
while(true)
{
if (SensorValue[S3]>30)
{ v=100; } // Сюда
else
v=0;

motor[motorB]=v;
motor[motorC]=v;
wait1Msec(1);
}


Слайд 31Контроль расстояния с совмещением регуляторов по датчику ультразвука





float e, v, kv=5;
while(true)
{

e=SensorValue[S3]-30;
if (e>0)
v=e*k;
else
v=0;
if (v>100) v=100;
motor[motorB]=v;
motor[motorC]=v;
wait1Msec(1);
}

Расчет отклонения по расстоянию
Запрет движения назад при отрицательном отклонении
Ограничение скорости не более 100

Слайд 32Контроль линии и расстояния с датчиком освещенности и ультразвука


float e, v,

kv=5;
while(true)
{ // Velocity control
e=SensorValue[S3]-30;
if (e>0)
v=e*kv;
else
v=0;
if (v>100) v=100;
motor[motorB]=v;
motor[motorC]=v;
wait1Msec(1);
}




int e, grey=45;
float u, v=50, kp=3;
while(true)
{ // Follow line
e=SensorValue[S1]-grey;
u=e*kp;

motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}


Добавление контроля расстояния до объекта через скорость

Слайд 33Движение по линии с контролем расстояния: результат совмещения





float u, v, e,

kp=3, kv=5;
while(true) {
e=SensorValue[S3]-30;
if(e>0)
v=e*kv;
else v=0;
if (v>100) v=100; //Вместо grey
e=SensorValue[S1]-SensorValue[S2];
u=e*kp;
motor[motorB]=v+u;
motor[motorC]=v-u;
wait1Msec(1);
}

Регулирование скорости движения в зависимости от расстояния до объекта спереди
Регулирование направления вдоль линии по двум датчикам освещенности
Подача комплекса управляющих воздействий на моторы

Слайд 34Контроль скорости с использованием интегральной составляющей





int ev;
float p,i=0,kv=0.5,ki=0.01;
while(true)
{ // Velocity

control
ev=SensorValue[S3]-30;
p=ev*kv;
i=i+ev*ki;
v=p+i;
...
wait1Msec(1);
}

При высоком коэффициенте kv теряется возможность управления направлением (робот сбивается с линии)
При низком коэффициенте kv робот не доезжает на заданное расстояние из-за нехватки мощности моторов
Интегральная составляющая суммирует ошибку и быстро увеличивает скорость

Слайд 35Контроль превышения скорости





int ev;
float p,i=0,kv=0.5,ki=0.01;
while(true)
{ // Velocity control
ev=SensorValue[S3]-30;
p=ev*kv;

i=i+ev*ki;
if (i>100) i=100;
v=p+i;
...
wait1Msec(1);
}

При высоком коэффициенте kv теряется возможность управления направлением (робот сбивается с линии)
При низком коэффициенте kv робот не доезжает на заданное расстояние из-за нехватки мощности моторов
Интегральная составляющая суммирует ошибку и быстро увеличивает скорость

Слайд 36Объезд препятствия





int grey1, grey2;
void objezd()
{
...
}
task main()
{ ...
while(true)
{
...


objezd();
...
}
}

Подпрограмма объезда вызывается при условии, что препятствие близко
Подпрограмма приостанавливает цикл регулирования, поскольку выполняется последовательно
Переменные grey1 и grey2 объявляются глобально для использования в основной программе и подпрограмме

Слайд 37Благодарю за внимание!
Сергей Александрович Филиппов
Физико-Математический лицей № 239
Санкт-Петербург
safilippov@gmail.com

Похожие презентации

Приоритетный национальный проект Образование в нашей школе 203
СТРУКТУРА СИСТЕМЫ САМОУПРАВЛЕНИЯ В МОУ СТАРОКАРАСУКСКАЯ СОШ 202
WSB НОВАЯ ЭРА ПРОФЕССИОНАЛЬНОГО БОКСА 390
ПРЕЗЕНТАЦИЯ предприятий-дипломантов Программы РОССИЙСКОЕ КАЧЕСТВО, лауреатов конкурса РОССИЙСКИЙ ЛИДЕР КАЧЕСТВА организаций-обладателей сертификата EFQM, а также победителей, лауреатов и дипломантов 3-ого Всероссийского конкурса менеджмента качества 415
Emerald Group Publishing Ведущее издательство научной литературы по менеджменту Мартин Дембовски MOSCOW 2009. 225
наступила золотая осень 351

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика