СОШ № 2 Крутась К П.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра и начала анализа. презентация
Содержание
- 1. Алгебра и начала анализа.
- 2. Эпиграф к уроку. Красота в единстве теории и практики.
- 3. Цели обучения, воспитания и развития. Рациональные способы
- 4. Задача1. Изобразить в координатной плоскости ХОУ заданные
- 5. Способ первый. Первый способ построения графика функции
- 6. Алгоритм построения. у1 = х –прямая
- 7. Демонстрация алгоритма построения.
- 8. Способ второй. Второй способ построения графика функции
- 9. Алгоритм построения Если
- 10. В построенном графике – прямой
- 11. Если
- 12. Аналогично построим графики - прямые в третьей
- 13. Выводы по уроку. А знаете ли вы
Слайд 1Алгебра и начала анализа.
Тема урока:
Преобразование графиков функций на координатной плоскости.
Учитель математики
Слайд 3Цели обучения, воспитания и развития.
Рациональные способы построения графиков функций.
Развитие пространственного и
логического мышления учащихся.
Воспитание творческого подхода к решению задач алгебры.
Воспитание творческого подхода к решению задач алгебры.
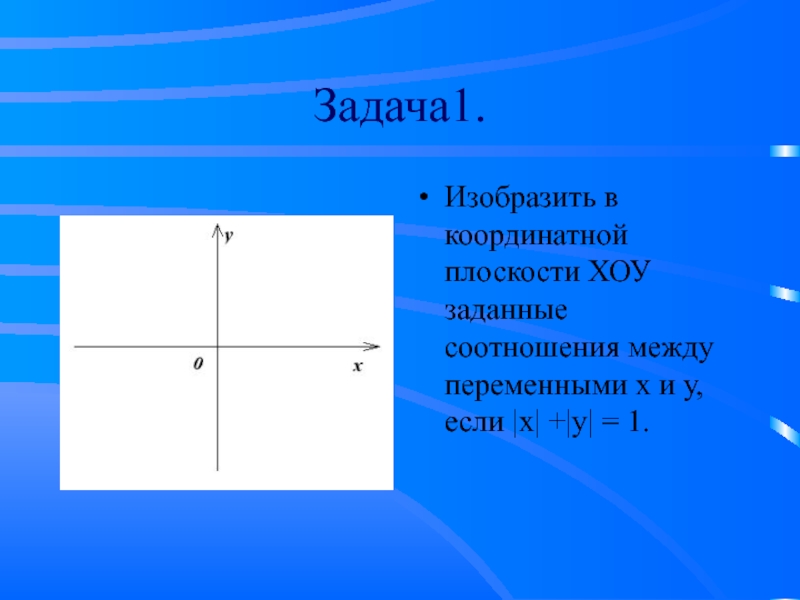
Слайд 4Задача1.
Изобразить в координатной плоскости ХОУ заданные соотношения между переменными х и
у, если |x| +|y| = 1.
Слайд 5Способ первый.
Первый способ построения графика функции – это построение требуемого графика
путем преобразований на координатной плоскости.
Данная функция |x|+|y|=1.
Выразим у через х;
|y|=-|x|+1.
Далее составим алгоритм построения графика функции |y|=-|x|+1.
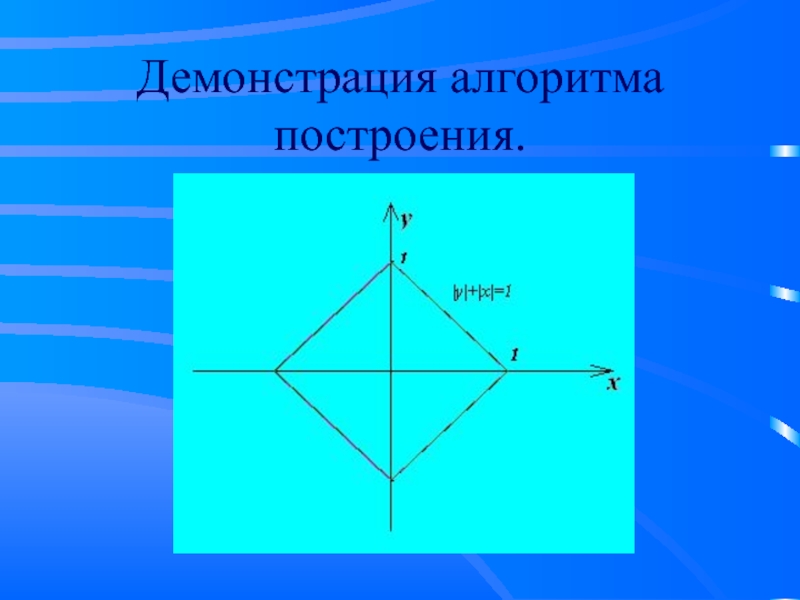
Слайд 6Алгоритм построения.
у1 = х –прямая – биссектриса 1 и 3
четверти координатной плоскости.
у2 = |x| – строим путем отображения графика функции у1 относительно оси (ох) в верхнюю полуплоскость.
у3 = -|x| – отображаем график функции у2 относительно оси (ох) в нижнюю полуплоскость.
у4 = -|x| + 1 –параллельный перенос графика функции у3 по оси (оу) на 1 вверх.
|y| = -|x| + 1 –отбрасываем часть графика у4 в нижней полуплоскости и оставшуюся часть отображаем относительно оси (ох) в нижнюю полуплоскость, тогда получим требуемый график заданной функции |y| + |x| = 1.
у2 = |x| – строим путем отображения графика функции у1 относительно оси (ох) в верхнюю полуплоскость.
у3 = -|x| – отображаем график функции у2 относительно оси (ох) в нижнюю полуплоскость.
у4 = -|x| + 1 –параллельный перенос графика функции у3 по оси (оу) на 1 вверх.
|y| = -|x| + 1 –отбрасываем часть графика у4 в нижней полуплоскости и оставшуюся часть отображаем относительно оси (ох) в нижнюю полуплоскость, тогда получим требуемый график заданной функции |y| + |x| = 1.
Слайд 8Способ второй.
Второй способ построения графика функции – это раскрытие модулей в
четвертях координатной плоскости с учётом знаков координатных осей.
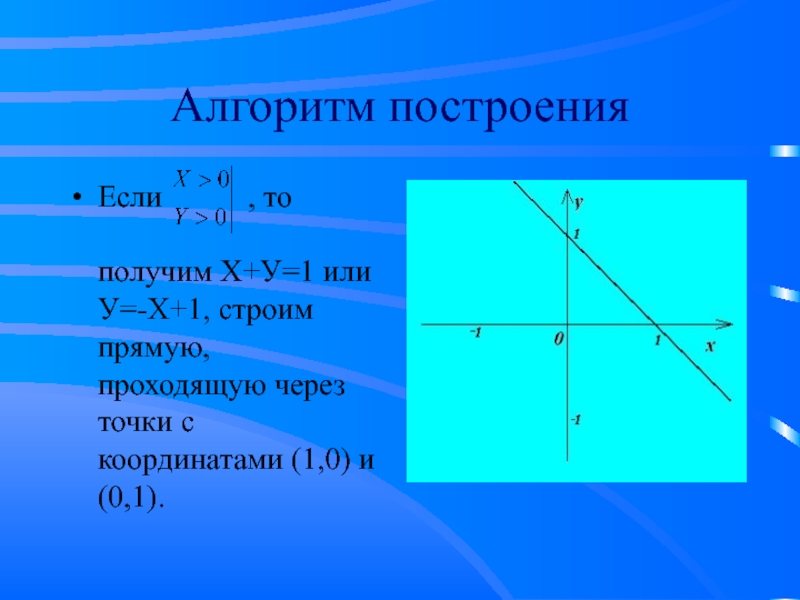
Слайд 9Алгоритм построения
Если , то
получим Х+У=1
или У=-Х+1, строим прямую, проходящую через точки с координатами (1,0) и (0,1).
Слайд 10В построенном графике – прямой уберем
, то на
координатной плоскости от прямой останется отрезок с концами на координатных осях
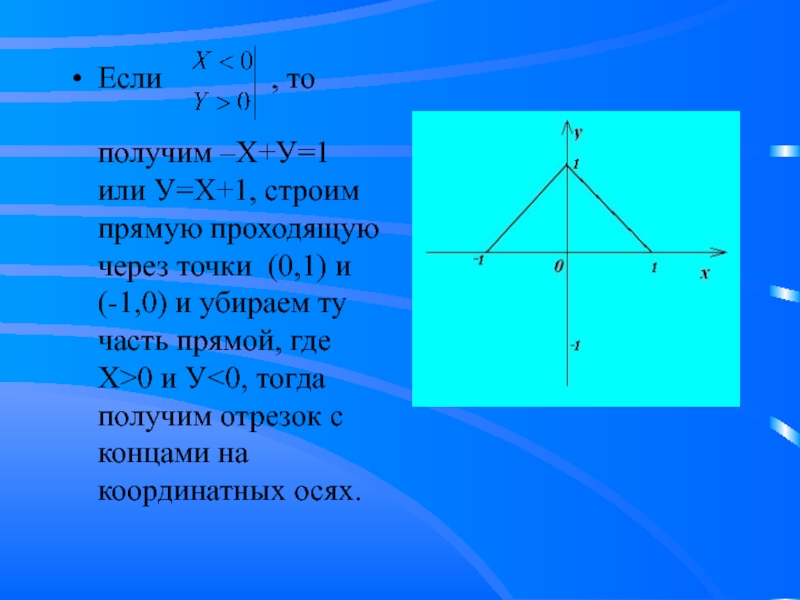
Слайд 11Если , то получим –Х+У=1
или У=Х+1, строим прямую проходящую через точки (0,1) и (-1,0) и убираем ту часть прямой, где Х>0 и У<0, тогда получим отрезок с концами на координатных осях.
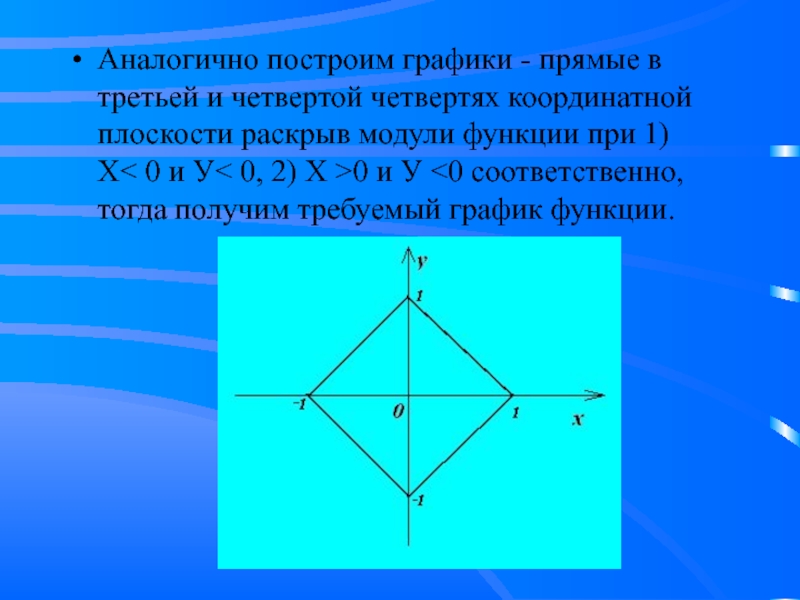
Слайд 12Аналогично построим графики - прямые в третьей и четвертой четвертях координатной
плоскости раскрыв модули функции при 1) Х< 0 и У< 0, 2) Х >0 и У <0 соответственно, тогда получим требуемый график функции.
Слайд 13Выводы по уроку.
А знаете ли вы другие способы построения графика функции?
Об
остальных способах поговорим на следующем уроке.
До свидания!
До свидания!