- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аффинные преобразования. презентация
Содержание
- 1. Аффинные преобразования.
- 2. Методологический паспорт. Тема: Аффинные преобразования плоскости. Проблема:
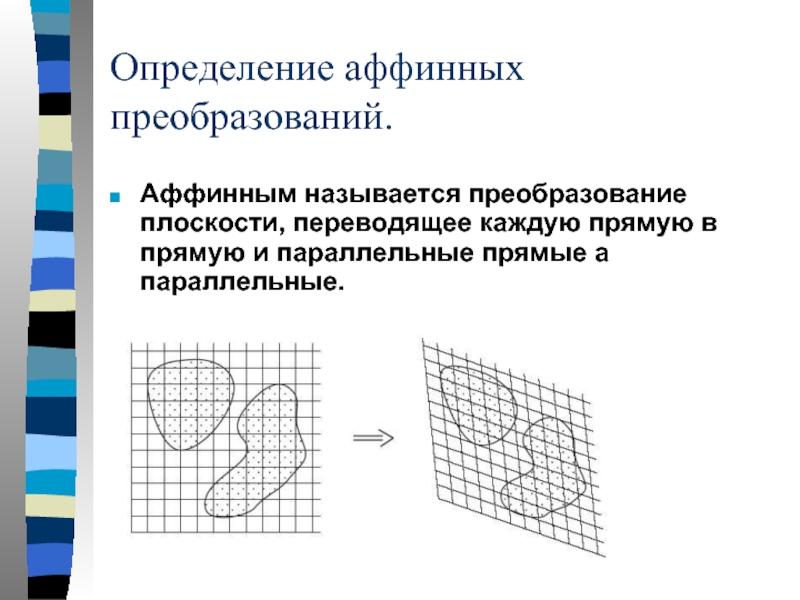
- 3. Определение аффинных преобразований. Аффинным называется преобразование плоскости,
- 4. Свойства аффинных преобразований. 1) аффинные преобразования сохраняют
- 5. Теорема о задании аффинных преобразований. Для
- 6. Докажем, что вершины параллелограммов построенных по треугольнику
- 7. Центры всех параллелограммов первой решетки переходят в
- 8. Неподвижные точки - основная характеристика аффинного
- 9. Возьмем С (С ∈ АВ), и покажем,
- 10. Метод аффинных преобразований. Использование преобразований для решения задач.
- 11. Задача №1. Доказать, что середины оснований трапеции,
- 12. Решение. Переведем треугольник AKD в равнобедренный
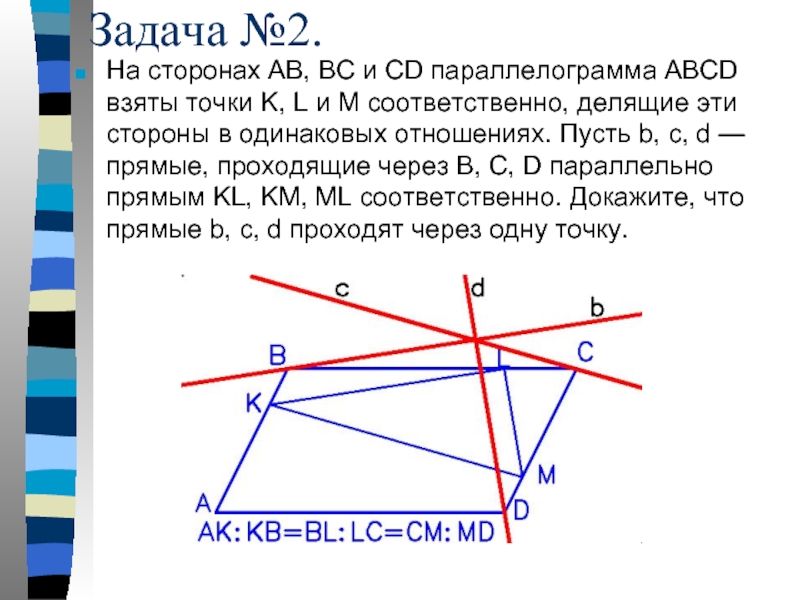
- 13. Задача №2. На сторонах AB, BC и
- 14. Решение. Переведем параллелограмм ABCD в квадрат
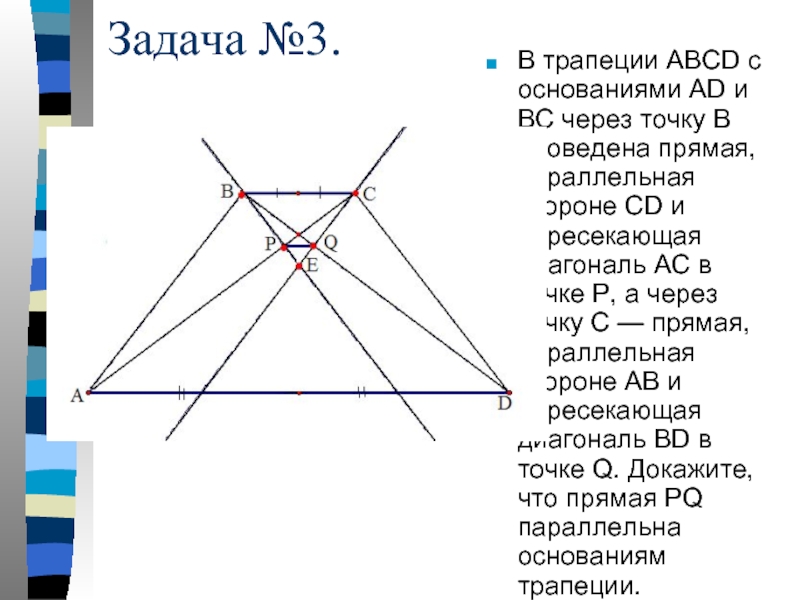
- 15. Задача №3. В трапеции ABCD с основаниями
- 16. Решение. Рассмотрим аффинное преобразование, переводящее ABCD в
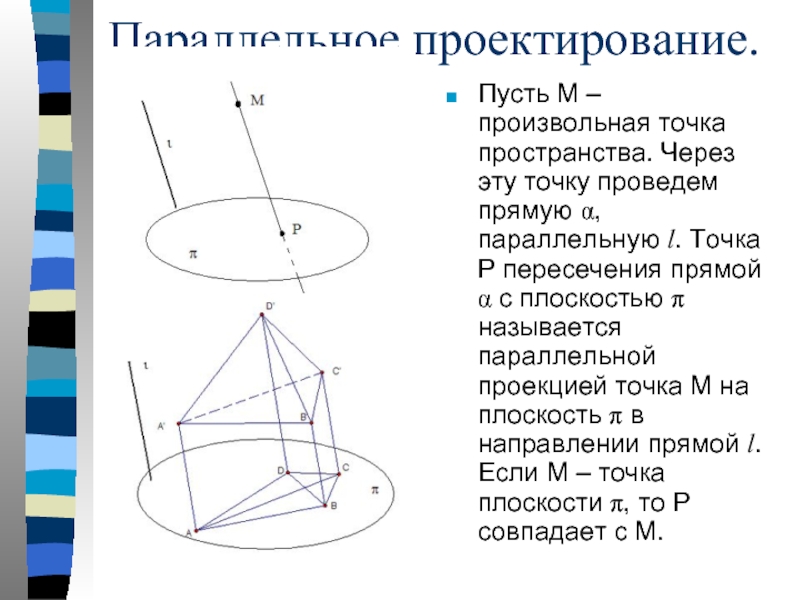
- 17. Параллельное проектирование. Пусть М – произвольная
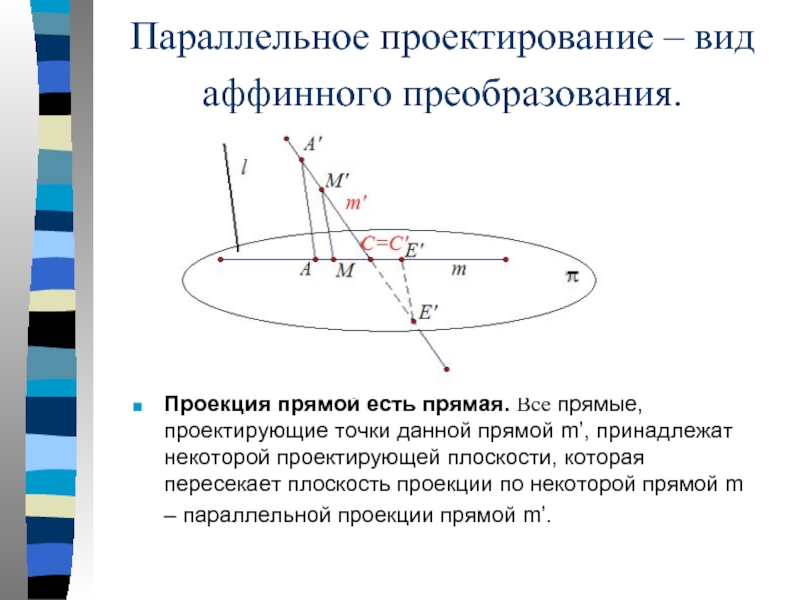
- 18. Параллельное проектирование – вид аффинного преобразования.
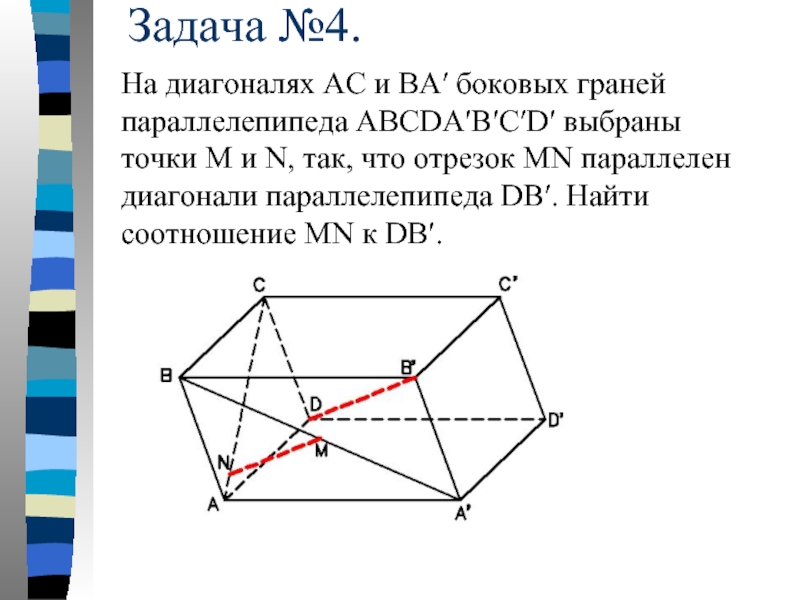
- 19. Задача №4. На диагоналях АС и
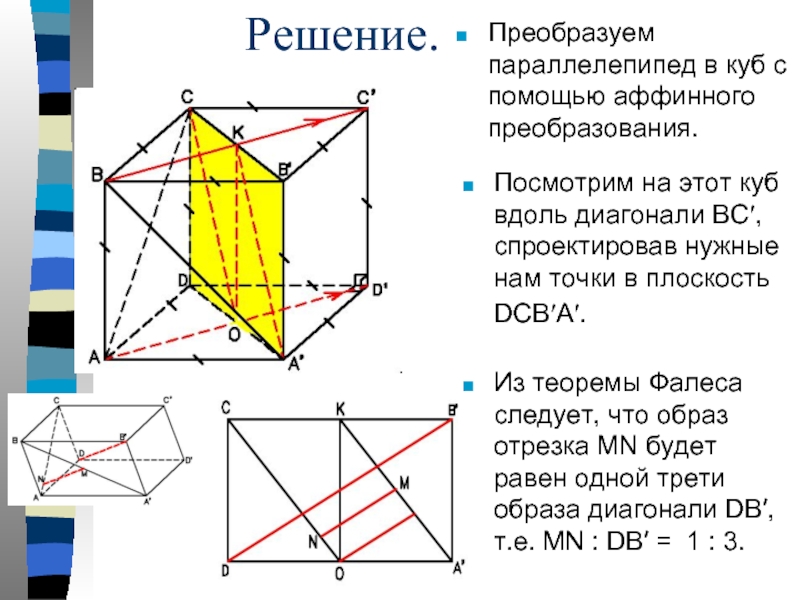
- 20. Преобразуем параллелепипед в куб с помощью аффинного
- 21. В пирамиде АВСD точки M, F и
- 22. Решение. В качестве плоскости
- 23. Выводы: Выполнение исследований позволило доказать, что аффинные
- 24. Библиография: 1) А.Д. Александров и др. «Геометрия».
Слайд 2Методологический паспорт.
Тема: Аффинные преобразования плоскости.
Проблема: Изучение понятия аффинных преобразований плоскости, их
Актуальность: Углубление знаний по теме позволило с большей легкостью решать планиметрические задачи, задачи на соотношения отрезков.
Объект исследования: Аффинные преобразования фигур на плоскости, параллельное проектирование, неподвижные точки аффинных преобразований.
Цель: Углубление знаний по теме, решение задач.
Задачи: Изучение теоретического материала, исследование свойств различных видов аффинных преобразований, решение задач.
Методы исследования: Теоретический и практический.
Слайд 3Определение аффинных преобразований.
Аффинным называется преобразование плоскости, переводящее каждую прямую в прямую
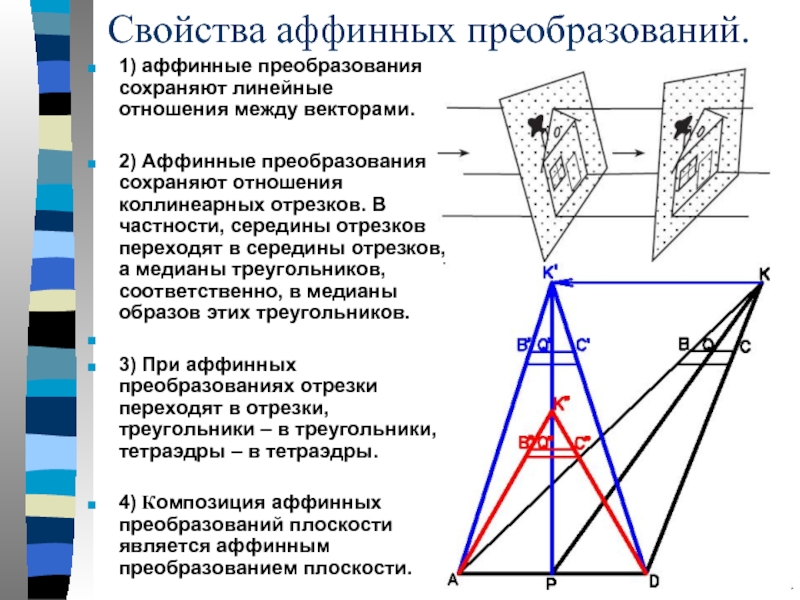
Слайд 4Свойства аффинных преобразований.
1) аффинные преобразования сохраняют линейные отношения между векторами.
2) Аффинные
3) При аффинных преобразованиях отрезки переходят в отрезки, треугольники – в треугольники, тетраэдры – в тетраэдры.
4) Композиция аффинных преобразований плоскости является аффинным преобразованием плоскости.
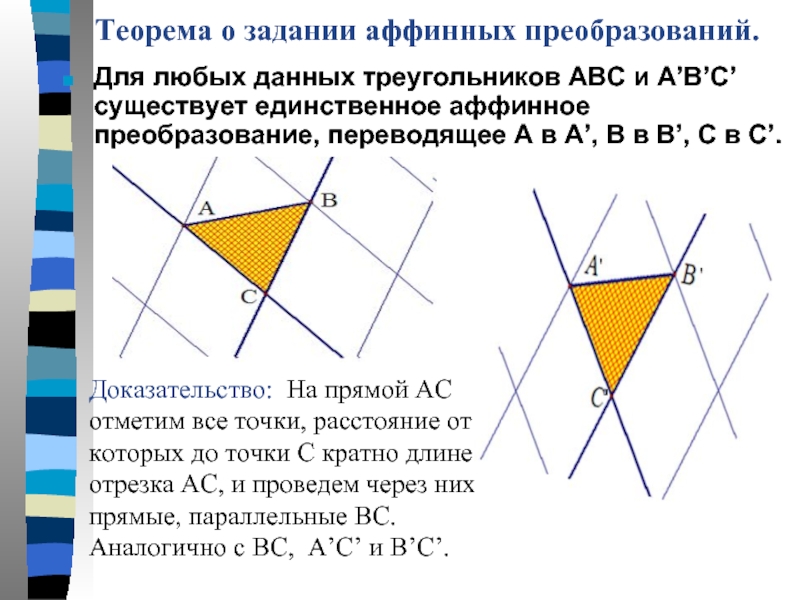
Слайд 5Теорема о задании аффинных преобразований.
Для любых данных треугольников АВС и
Доказательство: На прямой АС отметим все точки, расстояние от которых до точки С кратно длине отрезка АС, и проведем через них прямые, параллельные ВС. Аналогично с ВС, A’C’ и B’C’.
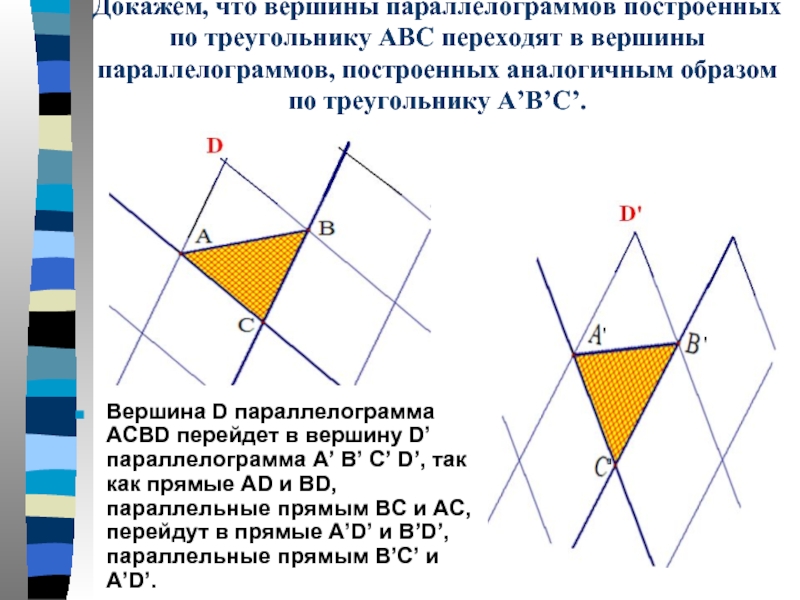
Слайд 6Докажем, что вершины параллелограммов построенных по треугольнику ABC переходят в вершины
Вершина D параллелограмма АСВD перейдет в вершину D’ параллелограмма А’ В’ С’ D’, так как прямые AD и BD, параллельные прямым ВС и АС, перейдут в прямые A’D’ и B’D’, параллельные прямым В’С’ и A’D’.
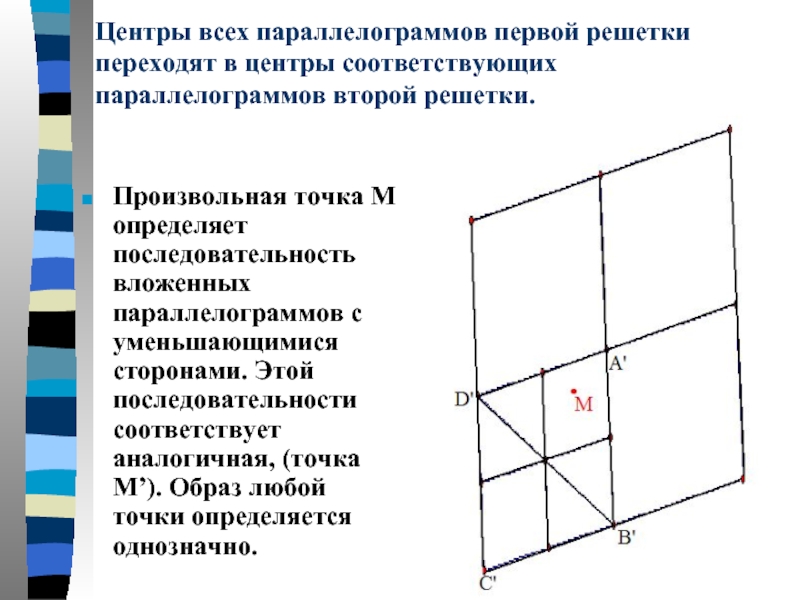
Слайд 7Центры всех параллелограммов первой решетки переходят в центры соответствующих параллелограммов второй
Произвольная точка М определяет последовательность вложенных параллелограммов с уменьшающимися сторонами. Этой последовательности соответствует аналогичная, (точка М’). Образ любой точки определяется однозначно.
Слайд 8Неподвижные точки -
основная характеристика аффинного преобразования. Возможны варианты:
1) Нет неподвижных
(Параллельный перенос)
2) Одна неподвижная точка.
(Центральная симметрия)
3) Если аффинное преобразование имеет две неподвижные точки А и В, то любая точка прямой АВ является неподвижной точкой этого преобразования.
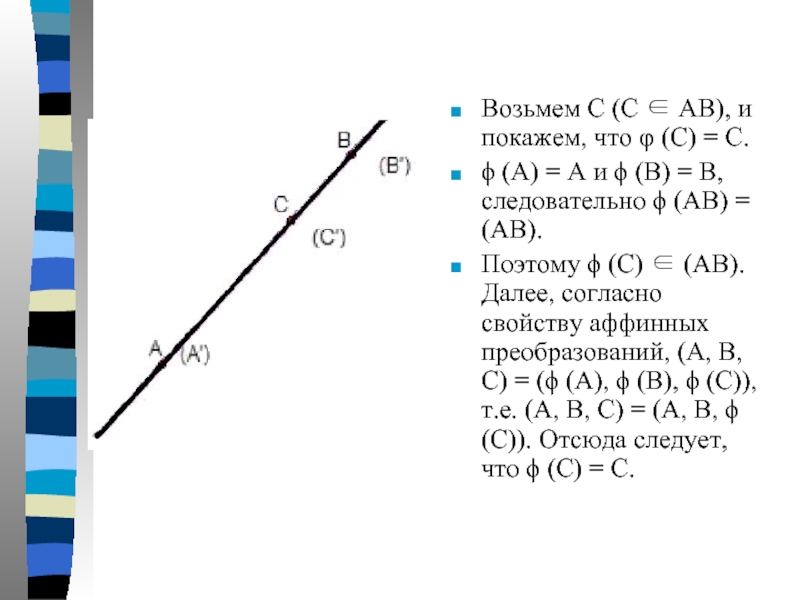
Слайд 9Возьмем С (С ∈ АВ), и покажем, что φ (С) =
ϕ (А) = А и ϕ (В) = В, следовательно ϕ (АВ) = (АВ).
Поэтому ϕ (С) ∈ (АВ). Далее, согласно свойству аффинных преобразований, (А, В, С) = (ϕ (А), ϕ (В), ϕ (С)), т.е. (А, В, С) = (А, В, ϕ (С)). Отсюда следует, что ϕ (С) = С.
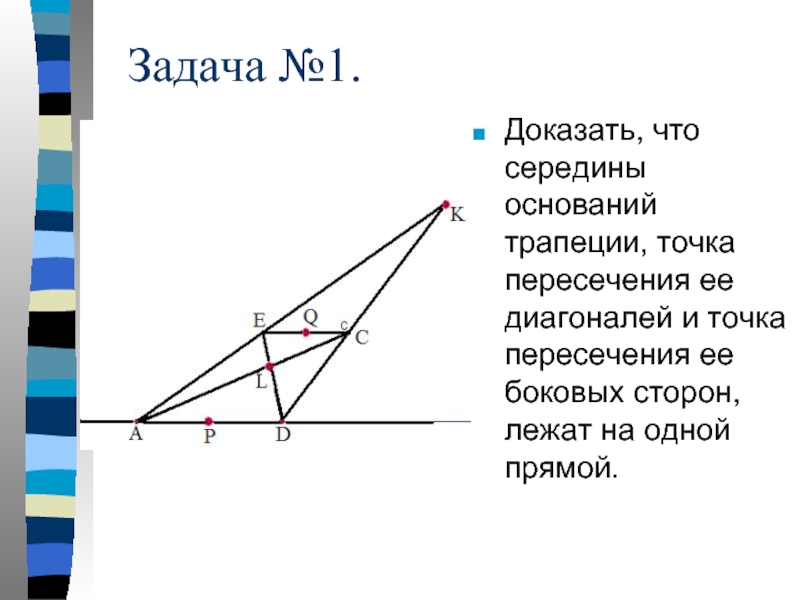
Слайд 11Задача №1.
Доказать, что середины оснований трапеции, точка пересечения ее диагоналей и
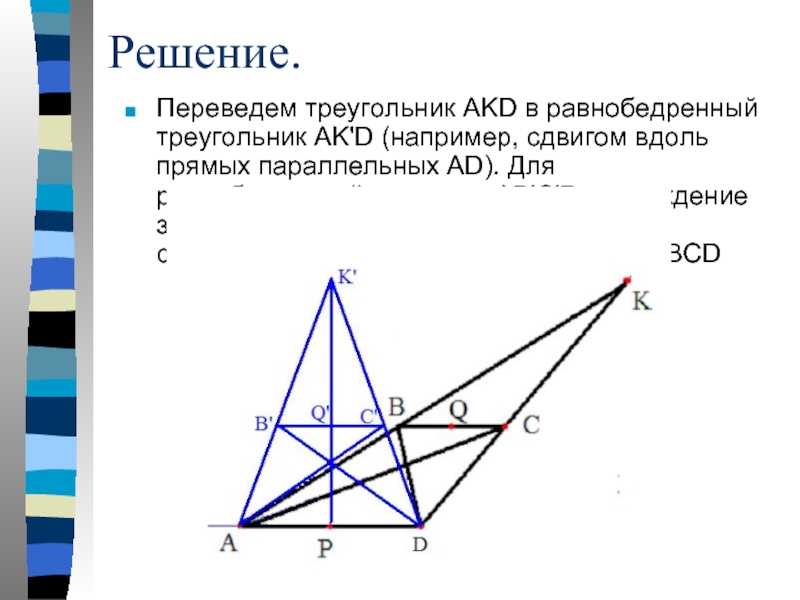
Слайд 12Решение.
Переведем треугольник AKD в равнобедренный треугольник AK'D (например, сдвигом вдоль
Слайд 13Задача №2.
На сторонах AB, BC и CD параллелограмма ABCD взяты точки
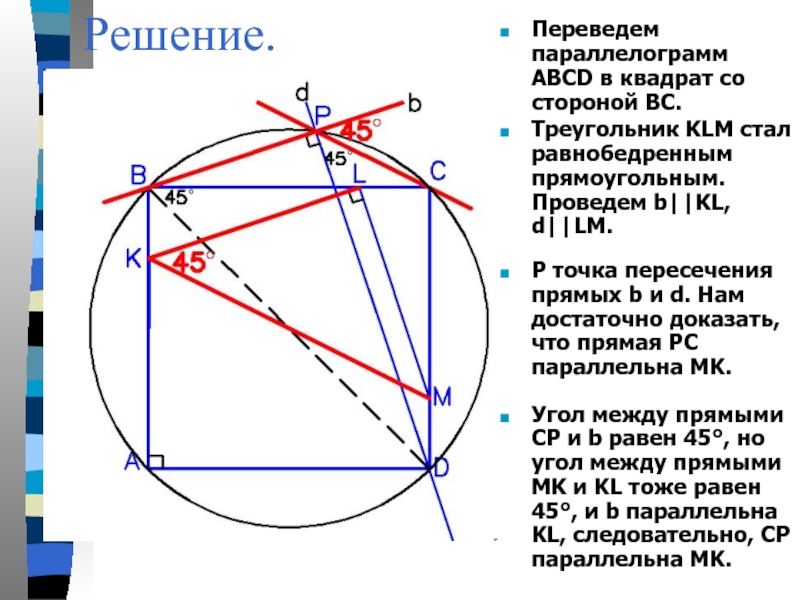
Слайд 14Решение.
Переведем параллелограмм ABCD в квадрат со стороной ВС.
P точка пересечения
Угол между прямыми CP и b равен 45°, но угол между прямыми MK и KL тоже равен 45°, и b параллельна KL, следовательно, CP параллельна MK.
Треугольник KLM стал равнобедренным прямоугольным. Проведем b||KL, d||LM.
Слайд 15Задача №3.
В трапеции ABCD с основаниями AD и BC через точку
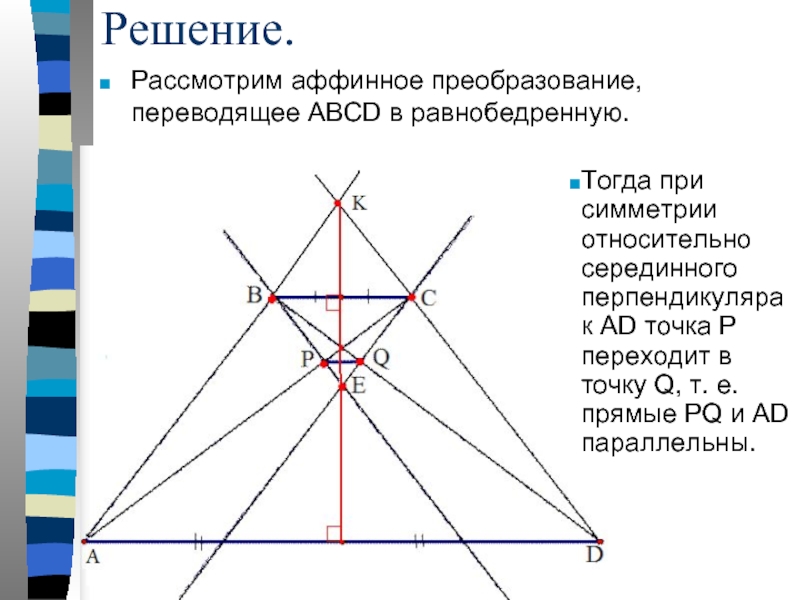
Слайд 16Решение.
Рассмотрим аффинное преобразование, переводящее ABCD в равнобедренную.
Тогда при симметрии относительно серединного
Слайд 17Параллельное проектирование.
Пусть М – произвольная точка пространства. Через эту точку
Слайд 18Параллельное проектирование – вид аффинного преобразования.
Проекция прямой есть прямая. Все
Слайд 19Задача №4.
На диагоналях АС и ВА′ боковых граней параллелепипеда АВСDA′B′C′D′ выбраны
Слайд 20Преобразуем параллелепипед в куб с помощью аффинного преобразования.
Посмотрим на этот
Из теоремы Фалеса следует, что образ отрезка MN будет равен одной трети образа диагонали DB′, т.е. MN : DB′ = 1 : 3.
Решение.
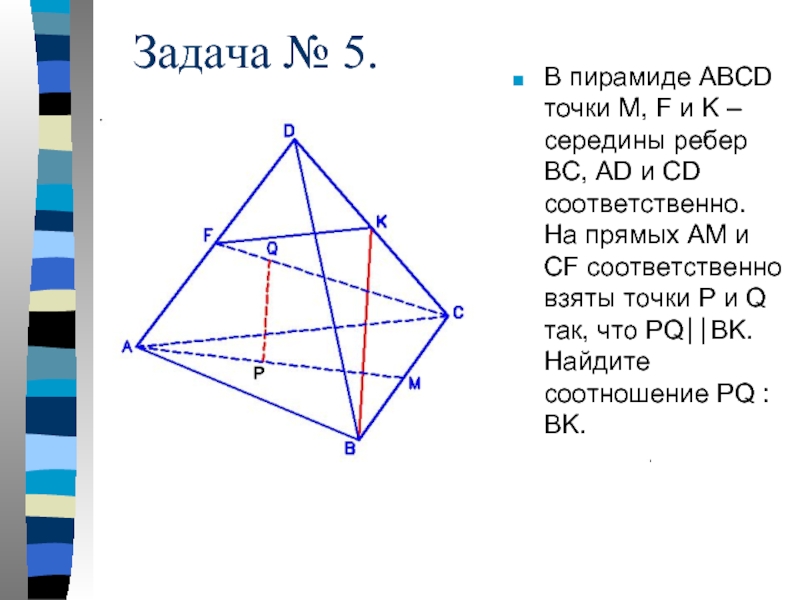
Слайд 21В пирамиде АВСD точки M, F и K – середины ребер
Задача № 5.
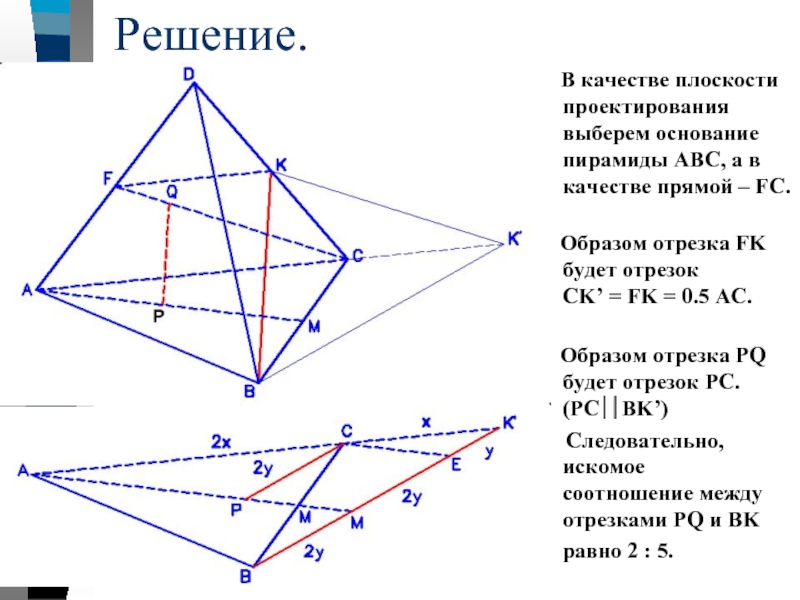
Слайд 22Решение.
В качестве плоскости проектирования выберем основание пирамиды АВС,
Образом отрезка FK будет отрезок CK’ = FK = 0.5 AC.
Образом отрезка PQ будет отрезок PC. (PC⎪⎪BK’)
Следовательно, искомое соотношение между отрезками PQ и BK равно 2 : 5.
Слайд 23Выводы:
Выполнение исследований позволило доказать, что аффинные преобразования на плоскости и в
Слайд 24Библиография:
1) А.Д. Александров и др. «Геометрия». Академический школьный учебник 11. Москва
2) Д.В. Беклемишев. «Курс аналитической геометрии и линейной алгебры». Москва 2007
3) С.П. Фиников. «Аналитическая геометрия. Курс лекций». Москва 2007
4) И.П. Егоров. «Высшая геометрия». Москва 2007
5) Ю. В. Садовничий и др. «Аналитическая геометрия. Курс лекция с задачами». Москва 2006
6) В. Мирошин «Параллельное проектирование в задачах»
7) Е. В. Потоскуев «Геометрия. 10 класс.» Москва 2004
8)А. Заславский «Геометрические преобразования» Санкт-Петербург 2004