Errors and how to correct them
Michael Lutz
based on Slides from the Co-ode OWL Tutorial available from http://www.co-ode.org/resources/tutorials/intro/
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
A Practical Introduction to Ontologies & OWL презентация
Содержание
- 1. A Practical Introduction to Ontologies & OWL
- 2. Overview Elephant Traps Property Domain & Range
- 3. Elephant Traps Common Errors in OWL generally
- 4. Property Domain & Range If a relation
- 5. Setting a Domain & Range Setting a
- 6. Semantics of Domain & Range Domain and
- 7. Exercise 10: IceCream and Domain
- 8. Trap: Property Domain Reclassification Any Class that
- 9. Property Characteristics Inverses – if property p
- 10. Functional Properties An individual can only have
- 11. Exercise 11: Functional Properties
- 12. Trap: Functional Property Misuse If a property
- 13. Intersection Classes aka “conjunction” This AND That
- 14. Intersection People often ask what the difference
- 15. Trap: Intersection There are 2 problems: Often
- 16. ComplementOf Classes aka “Negation” “Not” Not Something
- 17. ComplementOf Classes Commonly used to model 3
- 18. Exercise 12: Variations of VeggiePizza The ontology
- 19. Summary You should now be able to:
Слайд 2Overview
Elephant Traps
Property Domain & Range
Property Characteristics – functional properties
Intersection
Negation in OWL
– ComplementOf
Class expressions test
Class expressions test
Слайд 3Elephant Traps
Common Errors in OWL generally include:
Disjoint misuse – often used
on defined classes by mistake
Confusing AllValueFrom and SomeValuesFrom – some doesn’t imply only, and only doesn’t imply some
Forgetting to close class descriptions
Incorrect expectations of Domain and Range defined for properties
Incorrect use of Functional Properties
Using intersection (AND) instead of union (OR), where the members of the intersection are disjoint
Confusing AllValueFrom and SomeValuesFrom – some doesn’t imply only, and only doesn’t imply some
Forgetting to close class descriptions
Incorrect expectations of Domain and Range defined for properties
Incorrect use of Functional Properties
Using intersection (AND) instead of union (OR), where the members of the intersection are disjoint
Слайд 4Property Domain & Range
If a relation is:
subject_individual ? hasProperty ? object_individual
The
domain is the class of the subject individual
The range is the class of the object individual (or a datatype if hasProperty is a Datatype Property)
The range is the class of the object individual (or a datatype if hasProperty is a Datatype Property)
Слайд 5Setting a Domain & Range
Setting a domain & range on a
property has global implications
Be careful not to over-constrain your ontology
The domain & range can be set in the Properties Tab – just click Add named class(es) e.g. Setting a domain of Pizza on hasBase
Using a Universal Restriction on a Class is like setting a local range
Be careful not to over-constrain your ontology
The domain & range can be set in the Properties Tab – just click Add named class(es) e.g. Setting a domain of Pizza on hasBase
Using a Universal Restriction on a Class is like setting a local range
Слайд 6Semantics of Domain & Range
Domain and Range are not used to
restrict the interface
They are used by the reasoner to infer additional information about individuals
Any individual that uses a property with a domain set can be inferred to be a member of the domain class
the same holds for range
They are used by the reasoner to infer additional information about individuals
Any individual that uses a property with a domain set can be inferred to be a member of the domain class
the same holds for range
Слайд 8Trap: Property Domain Reclassification
Any Class that uses a property with a
domain set in an existential restriction will be inferred to be a subclass of the domain class
This is because all individuals in this class must have at least one relationship using this property – therefore, all members of this class must be members of the domain class
If these classes are disjoint with the domain then they will come out inconsistent – another reason to check all your disjoints are set
The same does not apply to range
This is because all individuals in this class must have at least one relationship using this property – therefore, all members of this class must be members of the domain class
If these classes are disjoint with the domain then they will come out inconsistent – another reason to check all your disjoints are set
The same does not apply to range
Слайд 9Property Characteristics
Inverses – if property p has inverse property q, and
p links A to B, then it can be inferred that q links B to A
Functional – For a given individual, the property takes only one value.
Inverse functional – The inverse of the property is functional.
Symmetric – If a property links A to B then it can be inferred that it links B to A.
Transitive – If a property links A to B and B to C then it can be inferred that it links A to C.
Functional – For a given individual, the property takes only one value.
Inverse functional – The inverse of the property is functional.
Symmetric – If a property links A to B then it can be inferred that it links B to A.
Transitive – If a property links A to B and B to C then it can be inferred that it links A to C.
Слайд 10Functional Properties
An individual can only have relationships with at most one
other individual along a functional property, e.g. if hasBase is functional this means: “Every Pizza can have at most one PizzaBase”
Description of DoubleBasePizza:
The reasoner finds this inconsistent
It looks like the interface is warning us that we can’t use the property more than once, but actually…
Description of DoubleBasePizza:
The reasoner finds this inconsistent
It looks like the interface is warning us that we can’t use the property more than once, but actually…
Слайд 12Trap: Functional Property Misuse
If a property is functional and is used
in several Existential restrictions on a class, the reasoner will infer that the filler classes must overlap
If any of the fillers are disjoint from each other then this cannot be the case and therefore causes an inconsistency
If they are not, no inconsistency is found!
If any of the fillers are disjoint from each other then this cannot be the case and therefore causes an inconsistency
If they are not, no inconsistency is found!
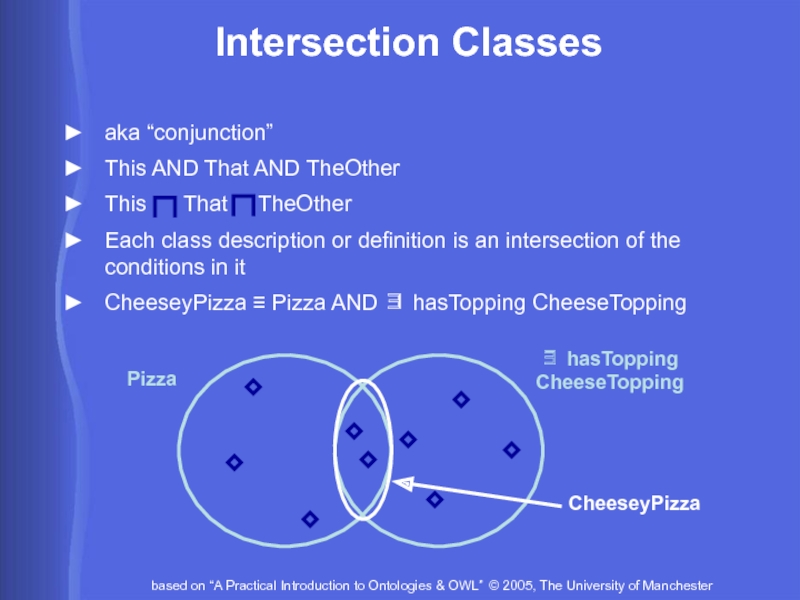
Слайд 13Intersection Classes
aka “conjunction”
This AND That AND TheOther
This That
TheOther
Each class description or definition is an intersection of the conditions in it
CheeseyPizza ≡ Pizza AND ∃ hasTopping CheeseTopping
Each class description or definition is an intersection of the conditions in it
CheeseyPizza ≡ Pizza AND ∃ hasTopping CheeseTopping
Слайд 14Intersection
People often ask what the difference is between using 2 existential
restrictions (which are, by default, in an intersection in the interface) and using a single restriction with a filler containing both the classes
=
Слайд 15Trap: Intersection
There are 2 problems:
Often we paraphrase “AND” when we logically
mean “OR”
The filler “CheeseTopping AND MeatTopping” cannot contain any individuals as they are disjoint, and is therefore inconsistent
If we correct this to OR, it is still wrong as we’ve got a class description that can be fulfilled by a Pizza with a single topping – either Cheese or Meat. If we had 2 existential restrictions, there would have to be at least 2 (disjoint) toppings
If we correct this to OR, it is still wrong as we’ve got a class description that can be fulfilled by a Pizza with a single topping – either Cheese or Meat. If we had 2 existential restrictions, there would have to be at least 2 (disjoint) toppings
≠
Слайд 16ComplementOf Classes
aka “Negation” “Not”
Not Something
¬ Something
owl:Thing
A
All individuals in here are members
of ¬A
Слайд 17ComplementOf Classes
Commonly used to model 3 things:
A is any C that
is not B
A does not have some relation with B
A only has relations with things that are not B
A does not have some relation with B
A only has relations with things that are not B
Слайд 18Exercise 12: Variations of VeggiePizza
The ontology used in this example will
be available at:
www.co-ode.org/ontologies/brokenPizza/
Слайд 19Summary
You should now be able to:
Avoid some of the more common
modelling errors in OWL
Appreciate that all OWL statements are reasoned with and many mistakes are only caught because of disjoints
Understand different characteristics of properties
Spot various similar looking statements in OWL are very different
Appreciate that all OWL statements are reasoned with and many mistakes are only caught because of disjoints
Understand different characteristics of properties
Spot various similar looking statements in OWL are very different