- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка F? (x)= f(x). презентация
Содержание
- 1. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка F? (x)= f(x).
- 2. 2. В чём заключается основное свойство первообразных?
- 3. 3. Назовите формулу Ньютона – Лейбница. Для
- 4. 4. Какая фигура называется криволинейной трапецией?
- 5. 5. Какие из рисунков являются криволинейными трапециями?
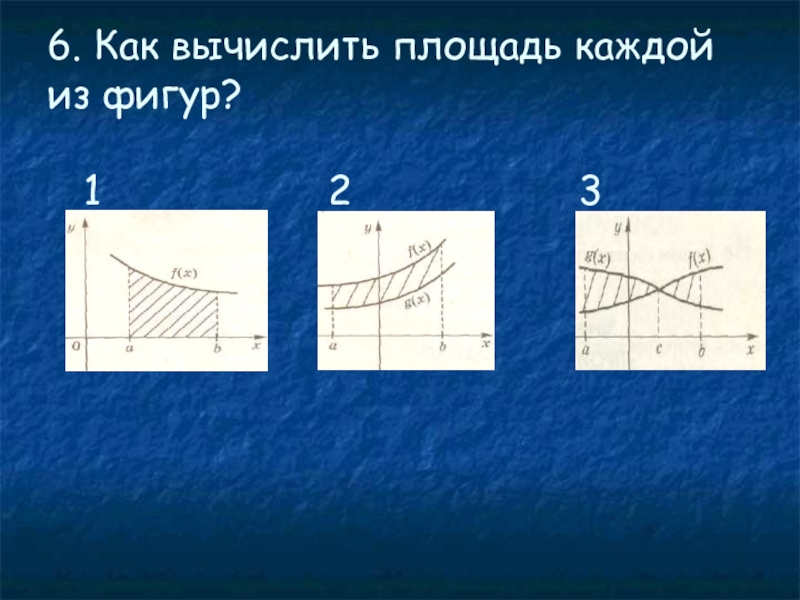
- 6. 6. Как вычислить площадь каждой из
- 7. "Применения интеграла". Тема урока:
- 8. Цели урока: Знать: применения интеграла;
- 9. Применение интеграла для вычисления объёмов тел вращения
- 10. Пусть V- объём тела
- 11. Разобьём отрезок [ а;b ] на n
- 12. Пример № 1 Пусть криволинейная трапеция опирается
- 13. При вращении трапеции вокруг оси Ох получаем
- 14. Работа переменной силы
- 15. P = c o n s t
- 16. А=∑(А1+А2+…+Аn) А1≈f(a)(X1-a); A2≈f(X1)(X2-X1) … An≈f(Xn-1)(b-Xn-1)
- 17. Вывод:
- 19. Домашнее задание: Стр 194-197, § 31 п.1,2. №№ 371, 374, 372(а).
Слайд 11.Что называется первообразной?
Функция F называется первообразной для функции f на заданном
промежутке, если для всех х из этого промежутка
F′ (x)= f(x).
F′ (x)= f(x).
Слайд 22. В чём заключается основное свойство первообразных?
Любая первообразная для
функции f на промежутке I может быть записана в виде F(x)+C, где F(x) – одна из первообразных для функции f (х) на промежутке I, С – произвольная постоянная.
Слайд 33. Назовите формулу Ньютона – Лейбница. Для чего она приме-няется?
b
∫
f(x)dx = F(b) - F(a),
а
Применяется при вычислении площадей криволинейных трапеций.
а
Применяется при вычислении площадей криволинейных трапеций.
Слайд 44. Какая фигура называется криволинейной трапецией?
Фигура, ограниченная графиком непрерывной функции
f(x), отрезком [a;b] и прямыми х=а и х=b, называют криволинейной трапецией.
Слайд 8Цели урока:
Знать:
применения интеграла;
формулы для вычисления объёма тел вращения
;
вычисления работы переменной силы;
Уметь:
применять эти формулы при решении прикладных задач.
вычисления работы переменной силы;
Уметь:
применять эти формулы при решении прикладных задач.
Слайд 10 Пусть V- объём тела и имеется такая прямая, что каждой точке
X отрезка [а;b] поставлено в соответствие единственное число S (x) – площадь сечения тела перпендикулярной оси ОХ плос-костью. Если S непрерывна на [a; b], то справедлива формула
b
V= ∫ S (x) d x
a
Слайд 11Разобьём отрезок [ а;b ] на n отрезков равной длины точками
x0 =а
v ≈S(x0)∆x +S(x1)∆x +…+S(xn-1)∆x= vn.
Точность этого приближённого равенства тем выше, чем тоньше
слои, на которые разрезано тело, т.е. чем больше n.
Поэтому vn→ v при n→∞.
По определению интеграла
Слайд 12Пример № 1
Пусть криволинейная трапеция опирается на отрезок [a; b] оси
Ох и ограничена сверху графиком функции f , неотрицательной и непрерывной на отрезке [ a; b ].
Слайд 13При вращении трапеции вокруг оси Ох получаем тело, объём которого находится
по формуле:
b
2
V=∫π f (x) d x
a



![4. Какая фигура называется криволинейной трапецией? Фигура, ограниченная графиком непрерывной функции f(x), отрезком [a;b] и](/img/tmb/1/95178/6449e06bf9560cb4db27cb1a974bdc3c-800x.jpg)





![Разобьём отрезок [ а;b ] на n отрезков равной длины точками x0 =а](/img/tmb/1/95178/7e80b8a05d15df636b8e7a394a5a5b57-800x.jpg)
![Пример № 1Пусть криволинейная трапеция опирается на отрезок [a; b] оси Ох и ограничена сверху](/img/tmb/1/95178/5eed369ae03bb62e21aa23d26ed8d140-800x.jpg)












