- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора И способы ее доказательства презентация
Содержание
- 1. Теорема Пифагора И способы ее доказательства
- 2. Теорема Пифагора и способы ее доказательства Содержание:
- 3. Теорема Пифагора и способы ее доказательства Исторический
- 4. Теорема Пифагора и способы ее доказательства Несколько
- 5. Теорема Пифагора и способы ее доказательства В
- 6. Теорема Пифагора и способы ее доказательства Карикатуры
- 7. Теорема Пифагора и способы ее доказательства Доказательство
- 8. Теорема Пифагора и способы ее доказательства Опустим
- 9. Теорема Пифагора и способы ее доказательства Доказательство
- 10. Теорема Пифагора и способы ее доказательства Здесь
- 11. Теорема Пифагора и способы ее доказательства Доказательство
- 12. Теорема Пифагора и способы ее доказательства Доказательство
- 13. Теорема Пифагора и способы ее доказательства Алгебраический
- 14. Теорема Пифагора и способы ее доказательства Четырехугольник
- 15. Теорема Пифагора и способы ее доказательства Это
- 16. Теорема Пифагора и способы ее доказательства Доказательство
- 17. Теорема Пифагора и способы ее доказательства S
- 18. Теорема Пифагора и способы ее доказательства
- 19. Теорема Пифагора и способы ее доказательства Фигуры
- 20. Получается что квадрат построенный на гипотенузе треугольника
Слайд 2Теорема Пифагора и способы ее доказательства
Содержание:
Исторический обзор
Алгебраический метод доказательства теоремы Пифагора
✓Доказательство теоремы Пифагора по Евклиду
✓Доказательство теоремы Пифагора по Басхари
✓Доказательство теоремы Пифагора по площади
✓Доказательство теоремы Пифагора по косинусу
✓Доказательство теоремы по методам Гофмана и Мёльманна
✓Наиболее привычный способ доказательства теоремы Пифагора
Карикатуры
Слайд 3Теорема Пифагора и способы ее доказательства
Исторический обзор
Исторический обзор начнем с древнего
Кантор (крупнейший немецкий историк математики) считает, что равенство 32 + 42 = 52 было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
Слайд 4Теорема Пифагора и способы ее доказательства
Несколько больше известно о теореме Пифагора
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Слайд 5Теорема Пифагора и способы ее доказательства
В настоящее время известно, что эта
На главную
Слайд 6Теорема Пифагора и способы ее доказательства
Карикатуры
Доказательство теоремы Пифагора учащиеся средних веков
Теорема Пифагора-одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2=a2+b2.
На главную
Слайд 7Теорема Пифагора и способы ее доказательства
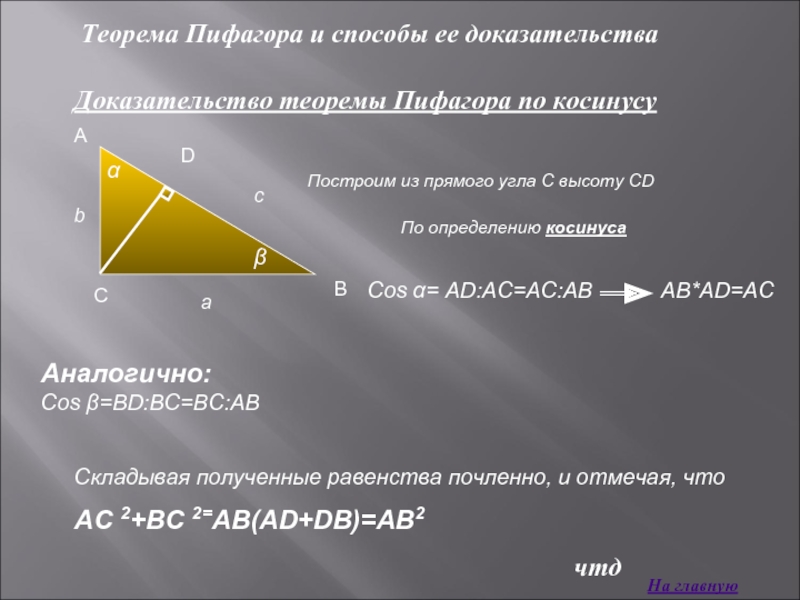
Доказательство теоремы Пифагора по косинусу
Построим из
По определению косинуса
Аналогично:
Cos β=BD:BC=BC:AB
Складывая полученные равенства почленно, и отмечая, что
АС 2+BС 2=AB(AD+DB)=AB2
чтд
На главную
Слайд 8Теорема Пифагора и способы ее доказательства
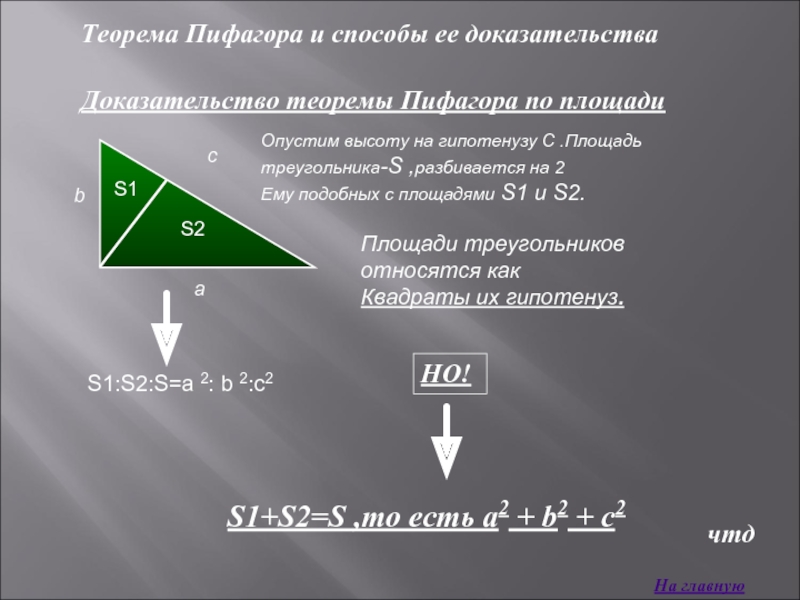
Опустим высоту на гипотенузу C .Площадь
Ему подобных с площадями S1 и S2.
Площади треугольников относятся как
Квадраты их гипотенуз.
Доказательство теоремы Пифагора по площади
НО!
чтд
На главную
Слайд 9Теорема Пифагора и способы ее доказательства
Доказательство теоремы Пифагора по Басхари
Это прямоугольный
Иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, XII в.). Рисунок сопровождало лишь одно слово: СМОТРИ! Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое древнее) занимает доказательство, использующее подобие.
Слайд 10Теорема Пифагора и способы ее доказательства
Здесь изображено два равных квадрата. Длина
На главную
Слайд 11Теорема Пифагора и способы ее доказательства
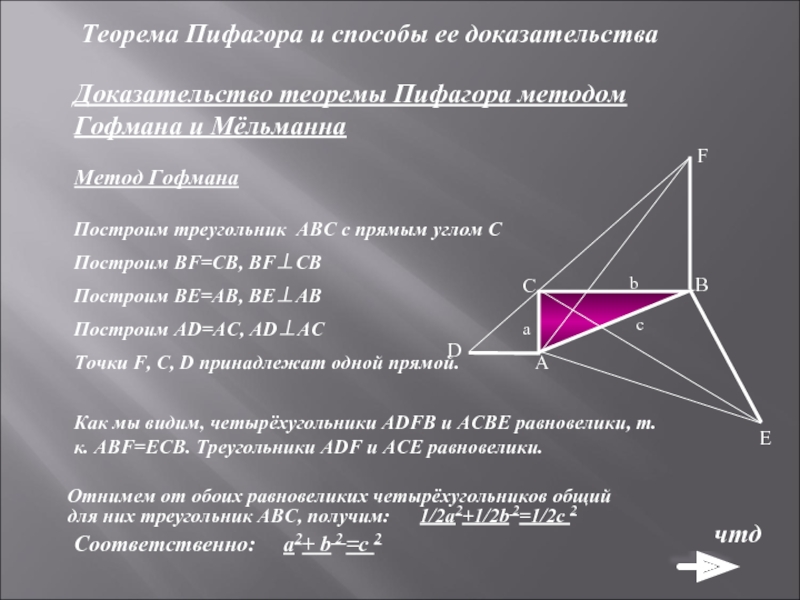
Доказательство теоремы Пифагора методом Гофмана и
Метод Гофмана
Построим треугольник ABC с прямым углом С
Построим BF=CB, BF⊥CB
Построим BE=AB, BE⊥AB
Построим AD=AC, AD⊥AC
Точки F, C, D принадлежат одной прямой.
Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ABF=ЕCB. Треугольники ADF и ACE равновелики.
Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2
чтд
Соответственно: а2+ b 2 =с 2
Слайд 12Теорема Пифагора и способы ее доказательства
Доказательство теоремы Пифагора методом Гофмана и
Метод Мёльманна
Площадь данного прямоугольника с одной стороны равна 0.5ab, с другой 0.5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r = 0.5(a+b-c)).
Имеем:
0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c)
Отсюда следует , что
с2=а2+b2
чтд
На главную
Слайд 13Теорема Пифагора и способы ее доказательства
Алгебраический способ доказательства теоремы Пифагора
A
Треугольники
Следовательно их гипотенузы равны
Слайд 14Теорема Пифагора и способы ее доказательства
Четырехугольник Р является квадратом
(Все стороны равны,
Равенство углов в четырехугольнике Р
доказывается следующим образом:
Пусть а и b – величины острых углов треугольника
Тогда ∠а + ∠b = 900
Угол А + (∠а +∠b) = 1800
1800 – 900 = 900
Угол А равен 900
Аналогичным способом находятся градусные меры остальных углов квадрата Р
Слайд 15Теорема Пифагора и способы ее доказательства
Это квадрат Q
Получим площадь квадрата Q
S(Q)
S(Q) = (а + b)2
S(P) = c2
S(T) = 1/2(ab)
(а + b)2 = c2 + 4(1/2(ab))
(а + b)2 = a 2 + 2ab + b 2
a 2+ 2ab + b 2 = c2 + 2ab
a 2 + b 2 = c2
чтд
На главную
Слайд 16Теорема Пифагора и способы ее доказательства
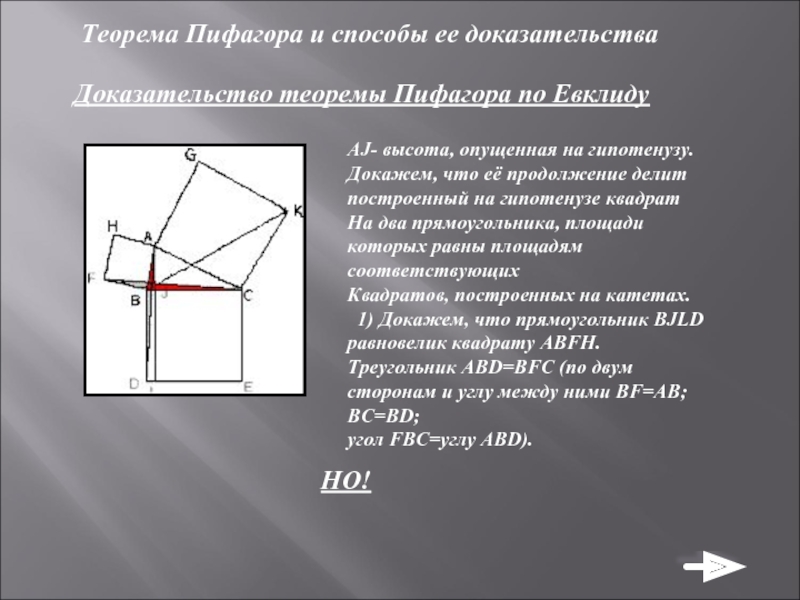
Доказательство теоремы Пифагора по Евклиду
AJ- высота,
Докажем, что её продолжение делит построенный на гипотенузе квадрат
На два прямоугольника, площади которых равны площадям соответствующих
Квадратов, построенных на катетах.
1) Докажем, что прямоугольник BJLD равновелик квадрату ABFH.
Треугольник ABD=BFC (по двум сторонам и углу между ними BF=AB; BC=BD;
угол FBC=углу ABD).
НО!
Слайд 17Теорема Пифагора и способы ее доказательства
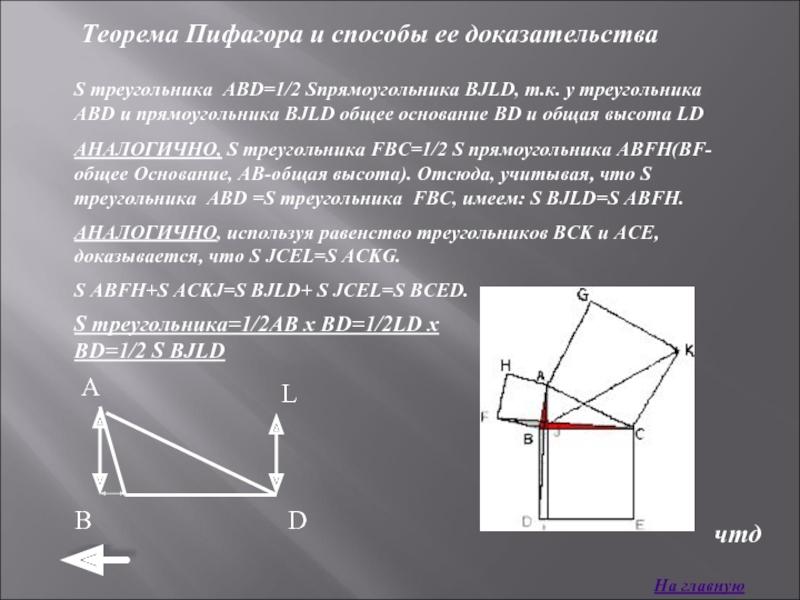
S треугольника ABD=1/2 Sпрямоугольника BJLD, т.к.
АНАЛОГИЧНО, S треугольника FBC=1/2 S прямоугольника ABFH(BF-общее Основание, AB-общая высота). Отсюда, учитывая, что S треугольника ABD =S треугольника FBC, имеем: S BJLD=S ABFH.
АНАЛОГИЧНО, используя равенство треугольников BCK и ACE, доказывается, что S JCEL=S ACKG.
S ABFH+S ACKJ=S BJLD+ S JCEL=S BCED.
S треугольника=1/2AB x BD=1/2LD x BD=1/2 S BJLD
чтд
На главную
Слайд 18Теорема Пифагора и способы ее доказательства
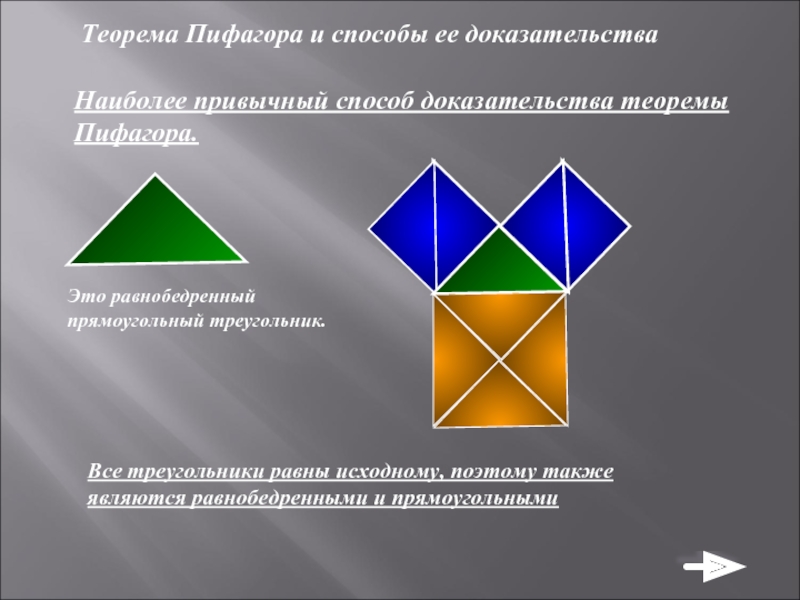
Наиболее привычный способ доказательства теоремы Пифагора.
Это
Все треугольники равны исходному, поэтому также являются равнобедренными и прямоугольными
Слайд 19Теорема Пифагора и способы ее доказательства
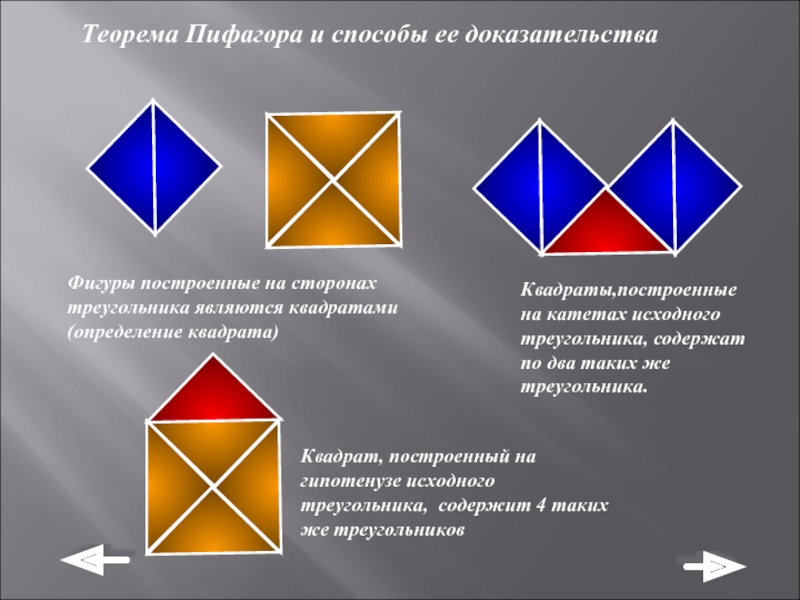
Фигуры построенные на сторонах треугольника являются
Квадраты,построенные на катетах исходного треугольника, содержат по два таких же треугольника.
Квадрат, построенный на гипотенузе исходного треугольника, содержит 4 таких же треугольников
Слайд 20Получается что квадрат построенный на гипотенузе треугольника равен сумме квадратов построенных
Теорема Пифагора и способы ее доказательства
a2 + b2 = c2
чтд
На главную