- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ презентация
Содержание
- 1. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
- 2. Функцию, заданную формулой y=logax , где
- 3. Основные свойства функции y=logax , а>0,
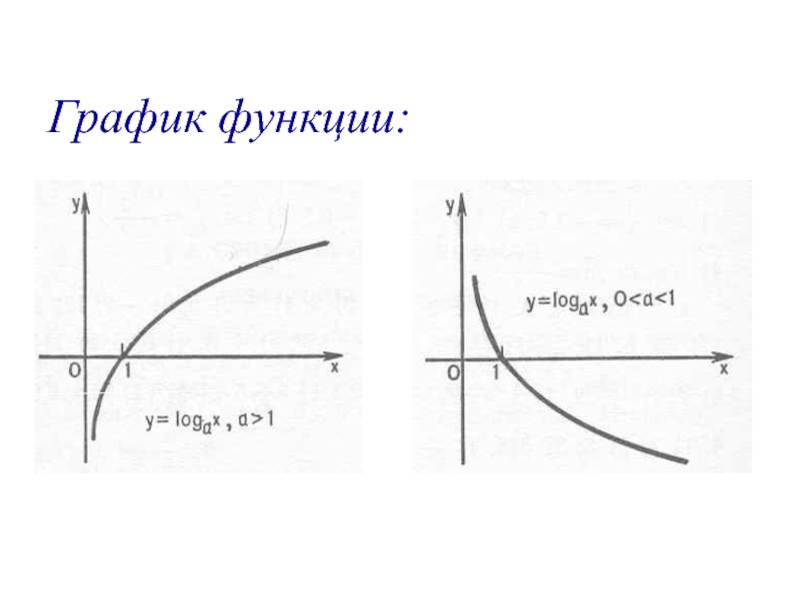
- 4. График функции:
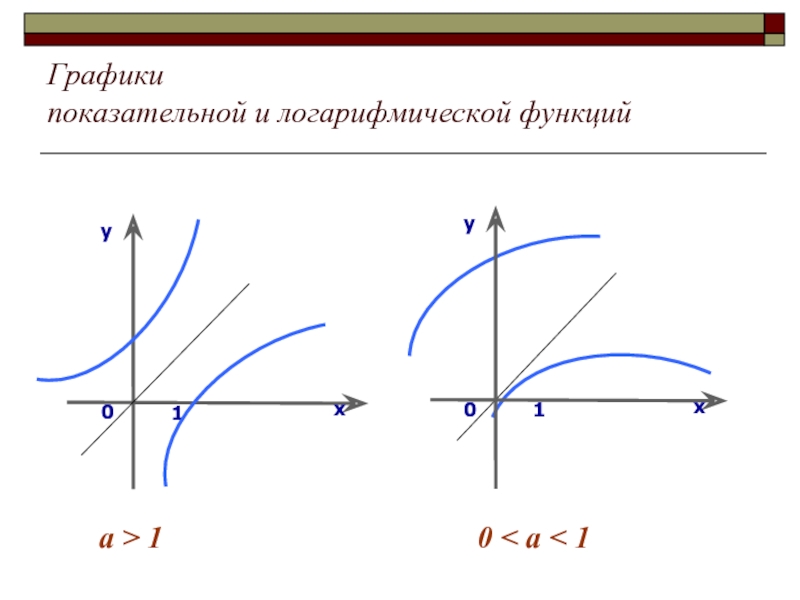
- 5. Графики показательной и логарифмической функций a > 1 0 < a < 1
- 6. Найти область определения функции: y=log2(х-5) Область определения
- 7. Сравнить: log37 и log310 Логарифмическая функция с
- 8. Перечислите основные свойства функции и
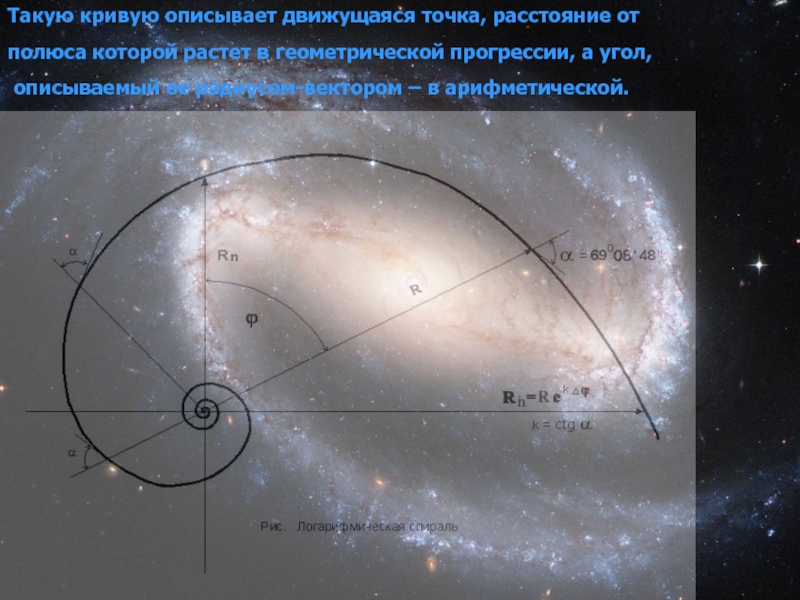
- 11. Такую кривую описывает движущаяся точка, расстояние
- 12. УРАГАН И ГАЛАКТИКА
Функцию, заданную формулой y=logax , где а>0, а ≠1 называют логарифмической функцией с основанием а.
Слайд 2Функцию, заданную формулой
y=logax ,
где а>0, а ≠1
называют логарифмической функцией с основанием
а.
Слайд 3Основные свойства функции
y=logax , а>0, а ≠1
D(y)=R+
E(y)=R
Нули: у=0 при х=1
Промежутки
знакопостоянства:
при 0<а<1 y>0 при хЄ(0;1);y<0 при хЄ(1;∞);
при а>1 y>0 при хЄ(1;∞);y<0 при хЄ(0;1).
Промежутки монотонности: при 0<а<1 функция убывает; при а>1 функция возрастает.
Экстремумы: нет.
Промежутки монотонности: при 0<а<1 функция убывает; при а>1 функция возрастает.
Экстремумы: нет.
Слайд 6Найти область определения функции:
y=log2(х-5)
Область определения логарифмической функции – R+ . Поэтому
данная функция определена для х, при которых х-5>0. Т.о. D(y)=(5;∞)
y=log2sin х
Данная функция определена для х, при которых sin х >0. Т.о. D(y)=(2πk; π+2πk ), k Є Z
y=log2sin х
Данная функция определена для х, при которых sin х >0. Т.о. D(y)=(2πk; π+2πk ), k Є Z
Слайд 7Сравнить:
log37 и log310
Логарифмическая функция с основанием, большим 1,возрастает на всей числовой
прямой. Т.к. 10>7, то log310 > log37 .
log¼7 и log¼10
Логарифмическая функция с основанием, меньшим 1,убывает на всей числовой прямой. Т.к. 7<10, то log¼7 > log¼10.
log¼7 и log¼10
Логарифмическая функция с основанием, меньшим 1,убывает на всей числовой прямой. Т.к. 7<10, то log¼7 > log¼10.
Слайд 8
Перечислите основные свойства функции и постройте её график:
y=log3(х-1)
D(y)= (1;∞)
E(y)=R
y=0 при
х=2
функция возрастает
y=log½х+1
D(y)=R+
E(y)=R
y=0 при х=2
функция убывает
функция возрастает
y=log½х+1
D(y)=R+
E(y)=R
y=0 при х=2
функция убывает
Слайд 11
Такую кривую описывает движущаяся точка, расстояние от
полюса которой растет в геометрической
прогрессии, а угол,
описываемый ее радиусом-вектором – в арифметической.
