- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
5 класс презентация
Содержание
- 1. 5 класс
- 2. Условные обозначения При работе с обучающей презентацией
- 3. Кроме того, обозначаются: Определения и
- 4. Натуральные числа Дробные числа Основы геометрии Решение уравнений Меры измерения величин выход
- 5. Натуральные числа Понятие Округление натуральных чисел Сравнение
- 6. Натуральные числа Понятие Для счета предметов
- 7. Любое натуральное число можно записать с помощью
- 8. Для чтения многозначных чисел их разбивают, начиная
- 9. Числовой ряд, в котором натуральные числа записаны
- 10. Любое натуральное число можно разложить на разряды:
- 11. Начертим луч ОХ так, чтобы
- 12. С числовыми шкалами в жизни мы
- 13. Натуральные числа. Понятие задачи 1. Определите, какой
- 14. Натуральные числа. Округление задачи 1. Округлите число
- 15. Натуральные числа Округление натуральных чисел Если
- 16. Натуральные числа Сравнение натуральных чисел При
- 17. Для сравнения чисел используют следующий алгоритм: если
- 18. Натуральные числа. Сравнение Задачи Какой знак сравнения
- 19. Натуральные числа Числовые и буквенные выражения При
- 20. Уравнением называют равенство, содержащее букву (переменную), значение
- 21. Натуральные числа. Буквенные выражения Задачи 1.Найти
- 22. Натуральные числа Сложение и вычитание натуральных чисел
- 23. Законы сложения Переместительный. Сумма чисел не изменяется
- 24. Рассмотрим задачу. Пешеход за два часа прошел
- 25. Законы вычитания Для того, чтобы вычесть сумму
- 26. Натуральные числа Умножение и деление натуральных чисел
- 27. Законы умножения 1. Переместительный. Произведение двух чисел
- 28. Решим задачу. 48 карандашей разложили поровну в
- 29. Законы деления 1. Ни одно число нельзя
- 30. Умножение и деление на разрядную единицу Разрядной
- 31. Натуральные числа. Умножение и деление чисел Выражения
- 32. Относительно деления тоже применяется распределительный закон. Рассмотрим
- 33. Натуральные числа. Умножение и деление чисел Произведение
- 34. Натуральные числа. Сложение и вычитание натуральных
- 35. Натуральные числа. Умножение и деление натуральных
- 36. Натуральные числа. Умножение и деление натуральных
- 37. Представьте в виде произведения выражение: 23а+37а= 85в-70в= 49х+х= 32с-с=
- 38. Найти значение выражения: 32+22=
- 39. Меры измерения величин Меры времени Меры
- 40. Меры измерения величин Меры времени Время измеряется
- 41. Например: 6 часов = суток =
- 42. Меры измерения времени Задачи Выразите в часах:
- 43. Меры измерения величин Меры длины Расстояние измеряется
- 44. Меры измерения величин. Меры длины
- 45. Меры измерения длины Задачи Выразите в сантиметрах
- 46. Меры измерения величин Меры веса Вес измеряется
- 47. Например: 5 кг = 0,05ц = 0,005
- 48. Меры измерения веса Задачи Сколько килограммов в
- 49. Меры измерения величин Меры площади Площадь поверхности
- 50. Меры измерения площади Задачи Выразите 36дм2 в
- 51. Меры измерения величин Меры объема Объем
- 52. Меры измерения объема Задачи Выразите 36дм3 в
- 53. Решение уравнений Левая часть уравнения
- 54. Решение уравнений Понятие Уравнением называют равенство,
- 55. Решение уравнений. Понятие Задачи Проверьте, является
- 56. Решение уравнений Левая часть уравнения
- 57. Аналогично рассуждая можно решить более сложное уравнение.
- 58. Левая часть уравнения представляет собой сумму Задачи
- 59. Решение уравнений Левая часть уравнения
- 60. Например: х - 35 = 65.
- 61. Например: 75 - х = 65.
- 62. Аналогично рассуждая можно решить более сложное уравнение.
- 63. Левая часть уравнения представляет собой разность Задачи
- 64. Решение уравнений Левая часть уравнения
- 65. Аналогично рассуждая можно решить более сложное уравнение.
- 66. Левая часть уравнения представляет собой произведение Задачи
- 67. Решение уравнений Левая часть уравнения
- 68. Например: х : 3 = 12.
- 69. Например: 75 : х = 5.
- 70. Аналогично рассуждая можно решить более сложное уравнение.
- 71. Левая часть уравнения представляет собой частное. Задачи.
- 72. Если в уравнении присутствует выражение с переменными,
- 73. Есть уравнения, левая часть которых представляют собой
- 74. Рассмотрим более сложные уравнения: Решить уравнение:(х-5)*63
- 75. Существуют уравнения, которые имеют два и более
- 76. Другие виды уравнений Задачи Сколько корней
- 77. Да, ваш ответ верен
- 78. Нет, ваш ответ не верен
- 79. Дробные числа Обыкновенные дроби Десятичные дроби выход
- 80. Обыкновенные дроби Понятие Сравнение обыкновенных дробей Сложение
- 81. Возьмем яблоко и разрежем его на 4
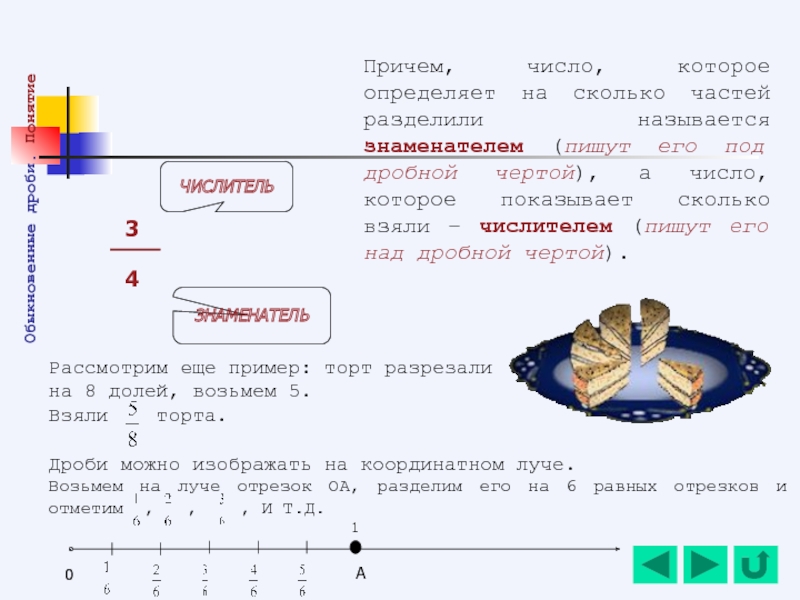
- 82. Рассмотрим еще пример: торт разрезали на 8
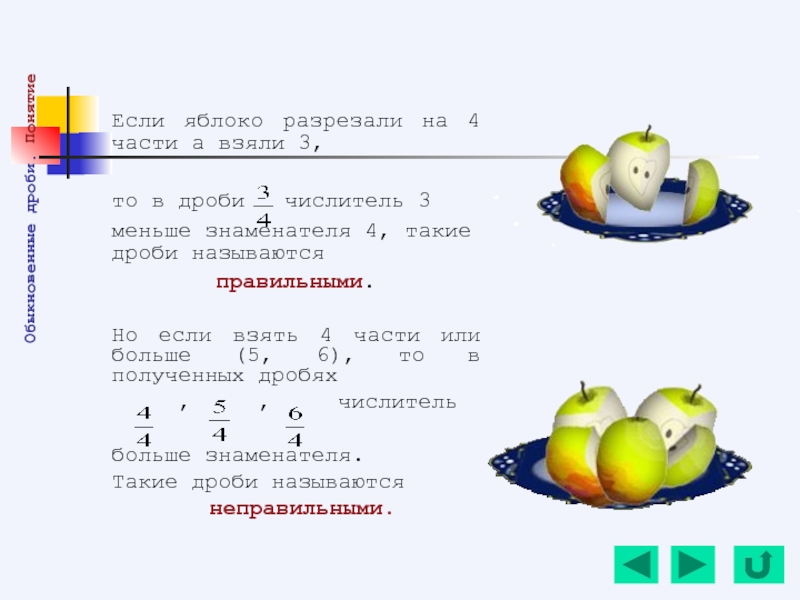
- 83. Если яблоко разрезали на 4 части а
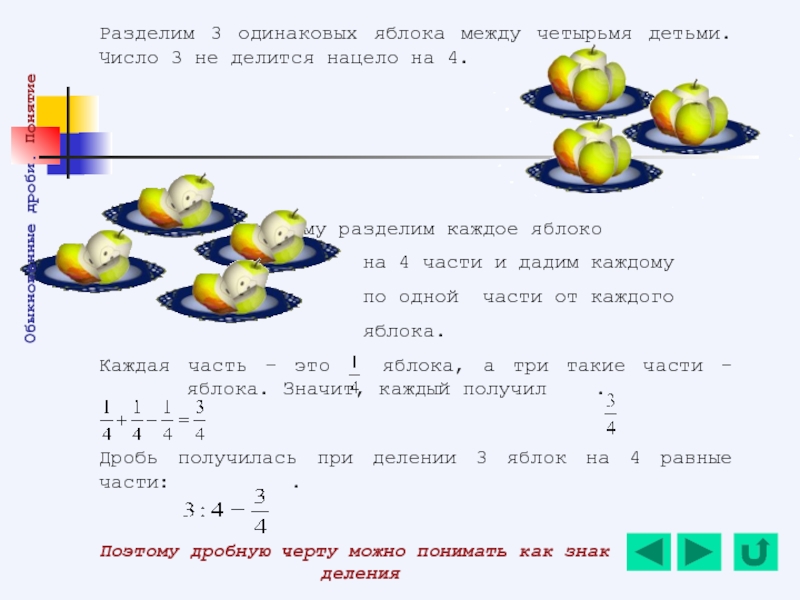
- 84. Разделим 3 одинаковых яблока между четырьмя детьми.
- 85. С помощью дробей можно записывать результат деления
- 86. Какая часть круга заштрихована? Какая часть
- 87. Обыкновенные дроби Сравнение дробей Разделим одно
- 88. Обыкновенные дроби. Сравнение дробей На координатном луче
- 89. Сравните дроби и
- 90. Обыкновенные дроби Сложение и вычитание обыкновенных
- 91. Обыкновенные дроби. Сложение и вычитание обыкновенных дробей
- 92. Выполните сложение дробей:
- 93. Разделим 5 яблок между 4 детьми. Можно
- 94. Обыкновенные дроби. Смешанные числа. Действия над ними
- 95. Обыкновенные дроби. Смешанные числа. Действия над ними
- 96. При вычитании смешанных чисел нужно поступить согласно
- 97. Выполните сложение дробей: Выполните
- 98. Десятичные дроби
- 99. Десятичные дроби Понятие. Например: 1 метр
- 100. Такие дроби у которых знаменателем являются числа
- 101. Какая десятичная дробь соответствует обыкновенной:
- 102. Если взять отрезок АВ, длиной 6см=60мм и
- 103. Сравним две десятичные дроби: 3,596 и 3,57.
- 104. Сравните десятичные дроби: 0,3 и 0,4 0,6 и
- 105. Десятичные дроби Сложение и вычитание десятичных
- 106. десятичные дроби. Сложение и вычитание десятичных дробей.
- 107. десятичные дроби. Сложение и вычитание десятичных дробей.
- 108. Десятичные дроби. Сложение и вычитание. Задачи.
- 109. Десятичные дроби Приближенное значение чисел. Округление.
- 110. Длина отрезка АВ ближе к 5см, чем
- 111. Десятичные дроби. Приближенное значение. Округление. Задачи.
- 112. Десятичные дроби Умножение десятичных чисел Умножим
- 113. Умножим десятичное число 1,83 на 10.
- 114. Алгоритм умножения десятичного числа на десятичное: Умножить
- 115. Десятичные дроби. Умножение. Задачи. Выполните умножение:
- 116. Десятичные дроби Деление десятичных чисел на
- 117. Чтобы разделить десятичное число на
- 118. Чтобы разделить десятичную дробь на десятичную нужно:
- 119. Десятичные дроби. Деление. Задачи. Выполните деление:
- 120. Десятичные дроби Проценты. Так как мы
- 121. Рассматривают три типа задач. 1.Известно число, необходимо
- 122. 2. Известна часть числа и ее процент,
- 123. 3. Известно число и часть числа. Необходимо
- 124. Десятичные дроби. Проценты Задачи. Выразите проценты
- 125. Десятичные дроби. Нахождение части числа по его
- 126. Десятичные дроби. Нахождение числа по его части
- 127. Десятичные дроби. Нахождение процента по числу и
- 128. Основы геометрии Точка. Отрезок.
- 129. Основы геометрии Точка. Отрезок. Возьмем в
- 130. Возьмем отрезок длиной 1см. Если отложить такой
- 131. В треугольнике отрезки AB, BC, CA называются
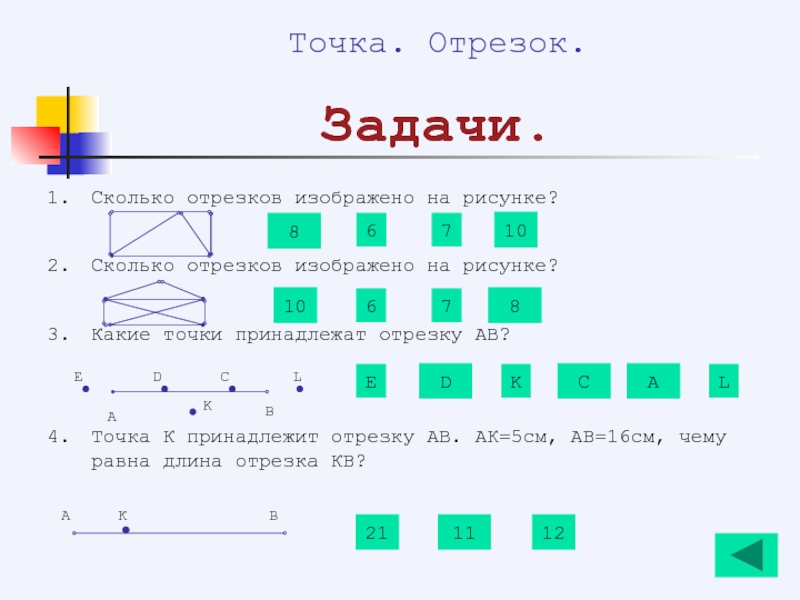
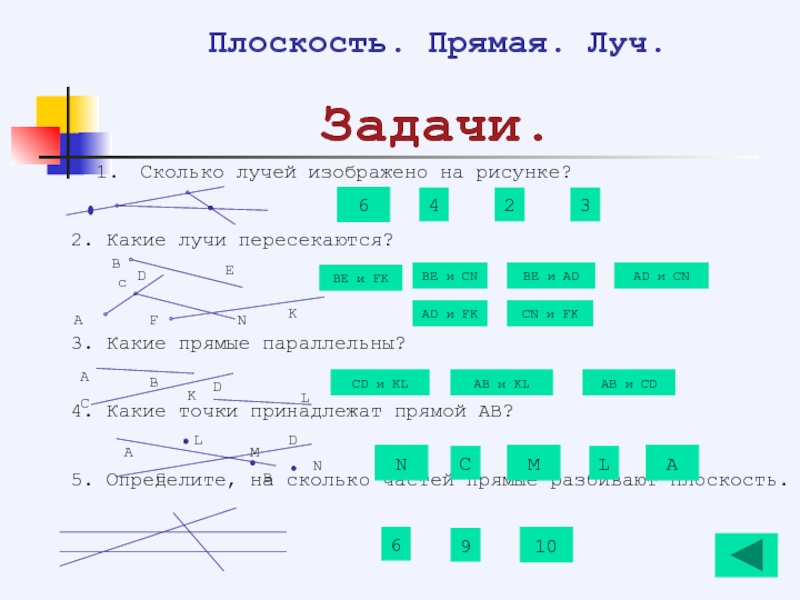
- 132. Сколько отрезков изображено на рисунке? Сколько
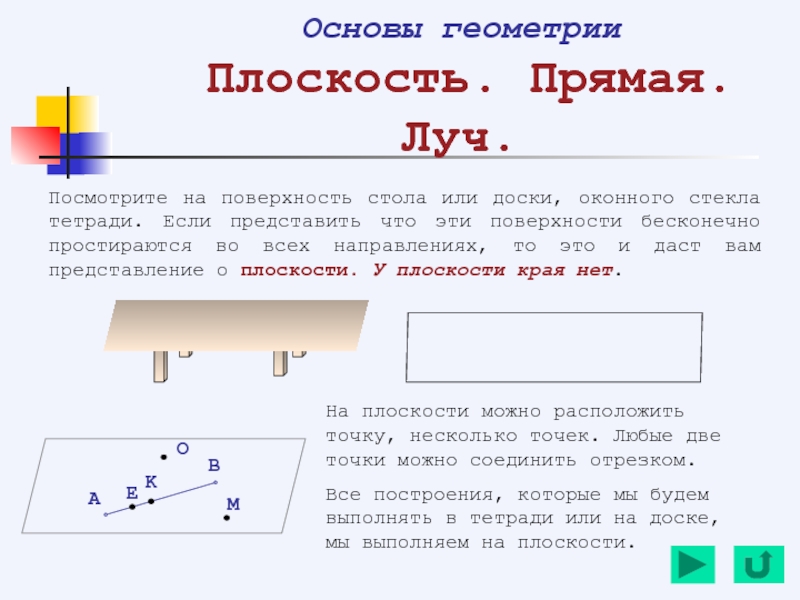
- 133. Основы геометрии Плоскость. Прямая. Луч. Посмотрите
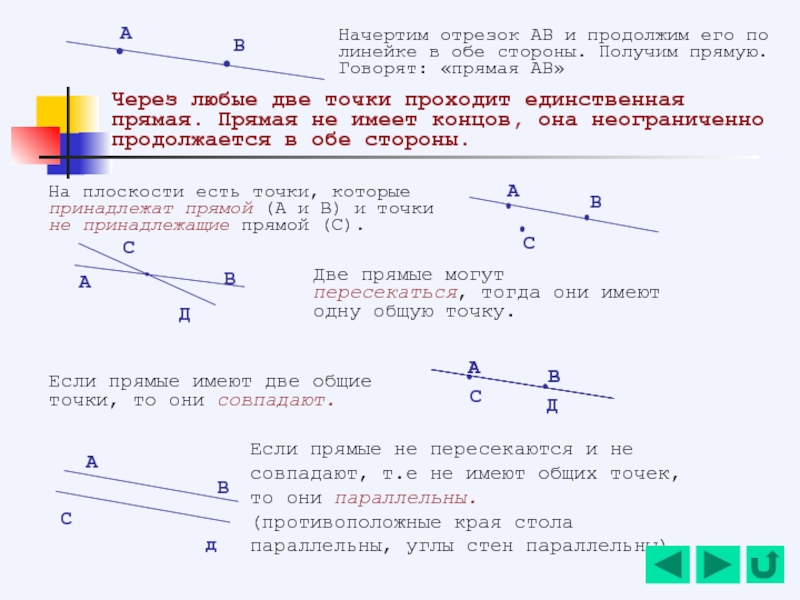
- 134. Начертим отрезок АВ и продолжим его по
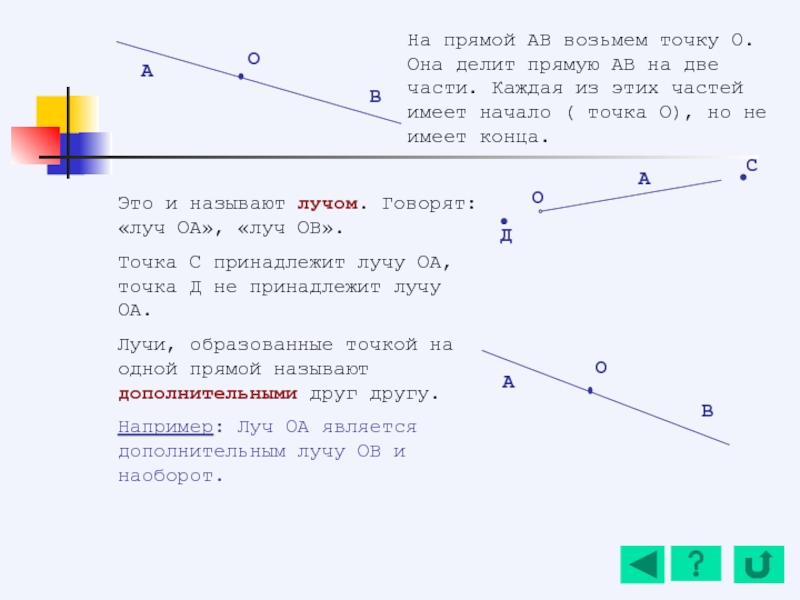
- 135. На прямой АВ возьмем точку О.
- 136. Сколько лучей изображено на рисунке? 2.
- 137. Есть точки, которые лежат внутри угла АОВ
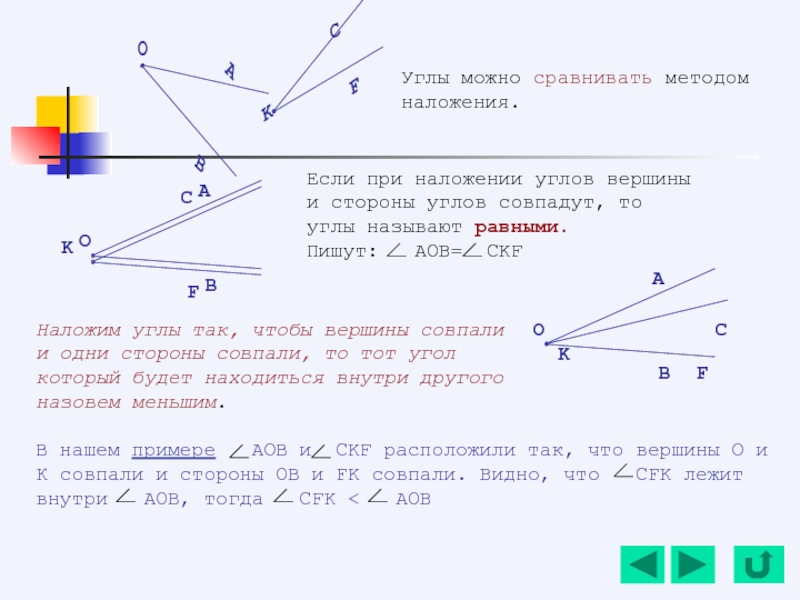
- 138. Наложим углы так, чтобы вершины совпали
- 139. Возьмем лист бумаги и согнем его
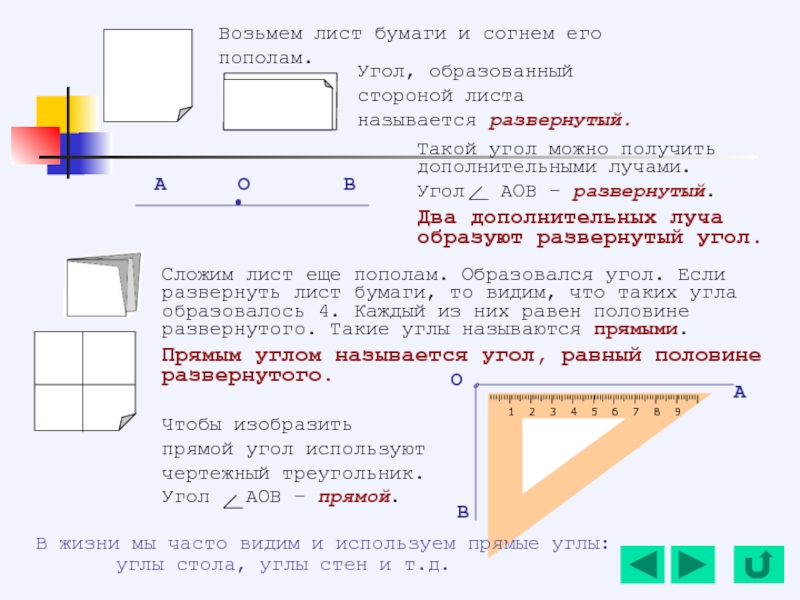
- 140. Для измерения углов применяют транспортир. Шкала транспортира
- 141. Равные углы имеют равную градусную меру, меньший
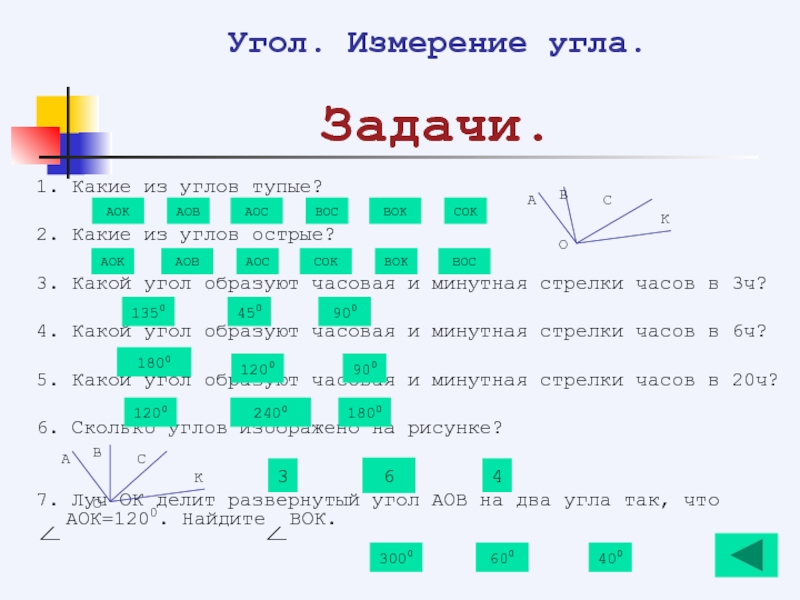
- 142. Угол. Измерение угла. Задачи. 1. Какие из
- 143. Основы геометрии. Многоугольники. Периметр и площадь многоугольников.
- 144. Геометрия изучает несколько основных фигур. Более
- 145. Если соединить четыре отрезка, то получим четырехугольник.
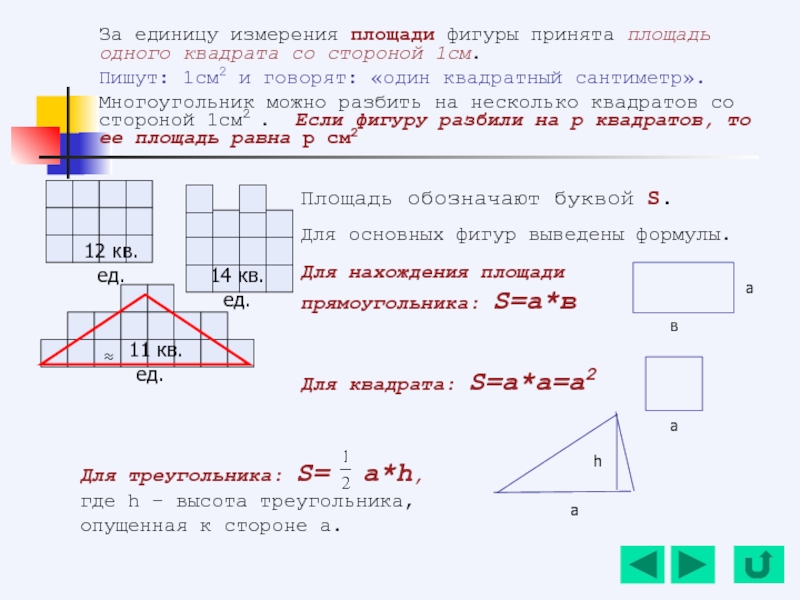
- 146. За единицу измерения площади фигуры принята площадь
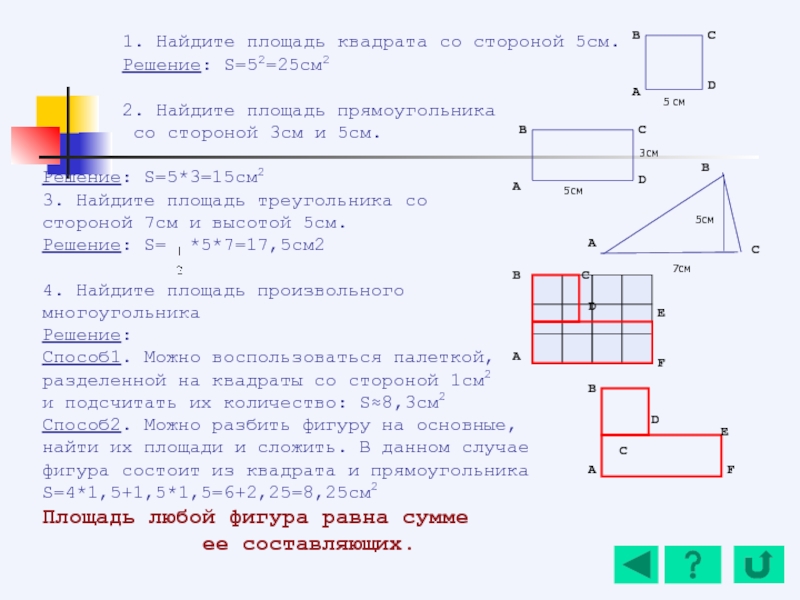
- 147. 1. Найдите площадь квадрата со стороной 5см.
- 148. Чему равен периметр многоугольника? Какая
- 149. Если соединить две любые точки окружности получится
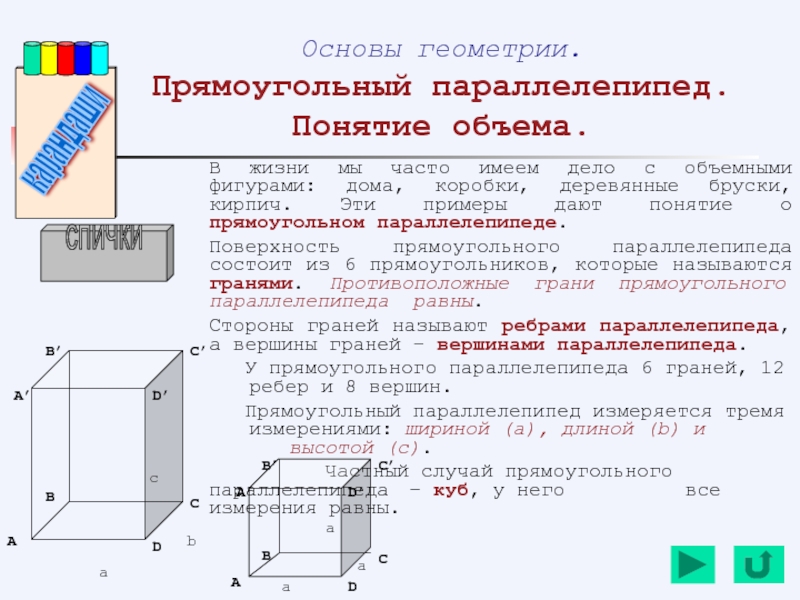
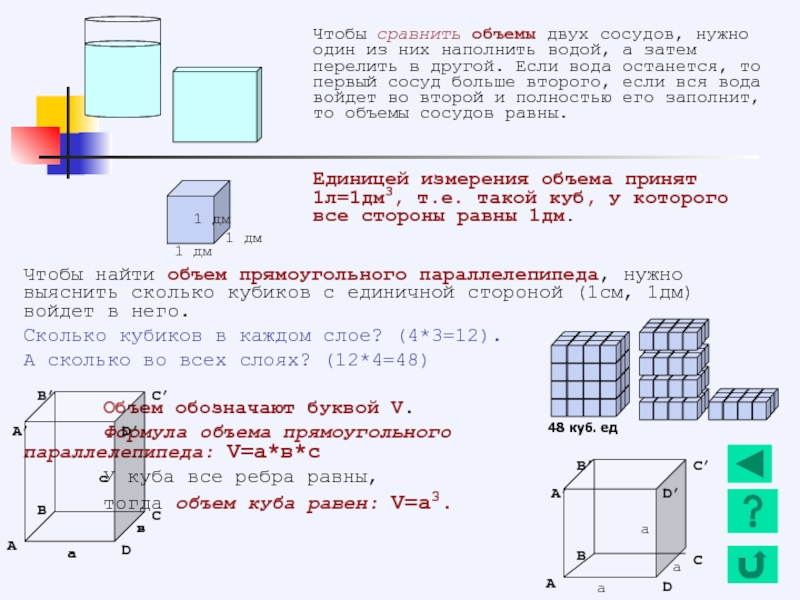
- 150. Основы геометрии. Прямоугольный параллелепипед. Понятие объема. В
- 151. Чтобы найти объем прямоугольного параллелепипеда, нужно выяснить
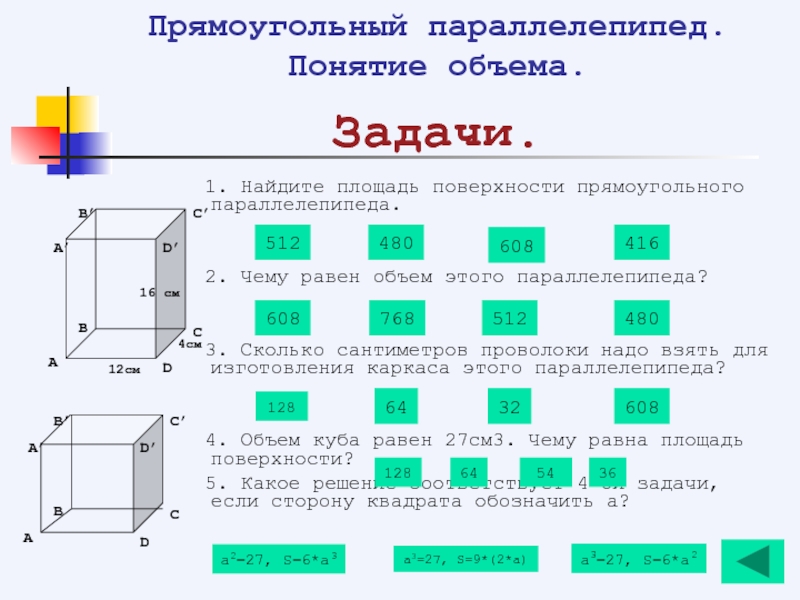
- 152. Прямоугольный параллелепипед. Понятие объема. Задачи.
- 153. Исторические сведения системы счисления Человечеством было придумано
- 154. В Древней Руси в качестве единиц измерения
- 155. Немецкого ученого Карла Гаусса называли королем
- 156. В наше время почти все народы пользуются
- 157. Первые единицы длины как в России, так
- 158. На Руси использовались в качестве измерения объема
Слайд 2Условные обозначения
При работе с обучающей презентацией вы можете воспользоваться кнопками:
- переход
- вызов задачника;
- переход к предыдущему слайду;
- интересные сведения из истории развития математики;
Если на слайде присутствует демонстрационная анимация, то она управляется щелком мыши.
- переход к следующему слайду внутри темы.
выход
- выход из обучающей презентации;
Слайд 3Кроме того, обозначаются:
Определения и понятия, которые нужно знать, выделены красным цветом.
Основные
Примеры выделены синим цветом.
Слайд 5Натуральные числа
Понятие
Округление натуральных чисел
Сравнение натуральных чисел
Сложение и вычитание натуральных чисел
Умножение и
Числовые и буквенные выражения
выход
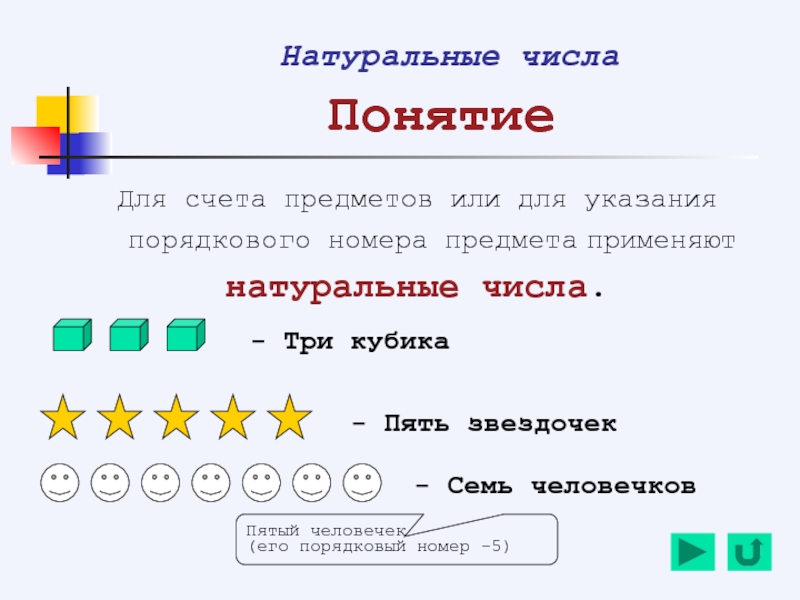
Слайд 6 Натуральные числа
Понятие
Для счета предметов или для указания порядкового номера предмета
натуральные числа.
- Три кубика
- Пять звездочек
- Семь человечков
Пятый человечек
(его порядковый номер -5)
Слайд 7Любое натуральное число можно записать с помощью десяти цифр
0, 1, 2,
Например: 32 ученика, 370 метров, 105 килограммов.
Такую запись чисел называют десятичной. Значение цифры зависит от ее места в записи числа.
Число разбивается на разряды: разряд единиц, разряд десятков, разряд сотен.
Например: В числе 583 – 3 единицы, 8 десятков, 5 сотен.
Цифра 0 в числе обозначает отсутствие данного разряда в десятичной записи числа.
Например: в числе 105 – цифра десятков отсутствует.
Натуральные числа. Понятие
Слайд 8Для чтения многозначных чисел их разбивают, начиная справа, на группы по
Эти группы называют классами.
Три цифры – класс единиц,
Три цифры – класс тысяч,
Три цифры – класс миллионов,
Три цифры - класс миллиардов, и т.д.
Например: число 15389000286 имеет 286 единиц в классе единиц, 0 единиц в классе тысяч, 389 – в классе миллионов, 15 единиц в классе миллиардов.
Натуральные числа. Понятие
Слайд 9Числовой ряд, в котором натуральные числа записаны по порядку, называется натуральным
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …
Единица является наименьшим натуральным числом, наибольшего натурального числа не существует.
Натуральные числа. Понятие
Слайд 10Любое натуральное число можно разложить на разряды:
123 = 1*100 + 2*10
5 891 = 5*1000 + 8*100 + 9*10 + 1
54 298 = 5*10000 + 4*1000 + 2*100 + 9*10 + 8
5 028 = 5*1000 + 2*10 + 8
30 204 = 3*10000 + 2*100 + 4.
И на оборот:
8*1000 + 3*100 + 5*10 + 2 = 8 352
9*10000 + 7*100 + 3*10 + 5 = 90 735.
Если обозначить буквой n какое-либо натуральное число, то n-1 – это число, ему предшествующее, а n+1 – это число последующее.
Например: n=15, тогда n-1=14, n+1=16.
Натуральные числа. Понятие
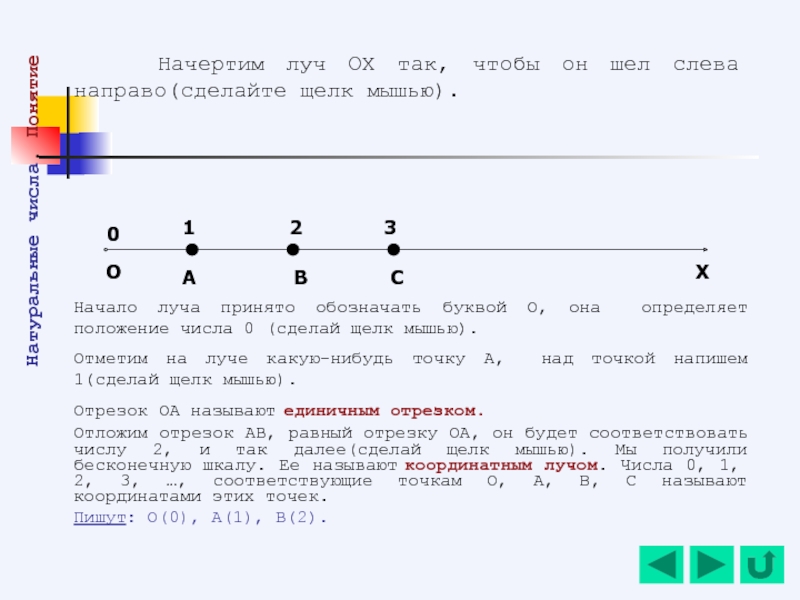
Слайд 11 Начертим луч ОХ так, чтобы он шел слева направо(сделайте
Начало луча принято обозначать буквой О, она определяет положение числа 0 (сделай щелк мышью).
Отметим на луче какую-нибудь точку А, над точкой напишем 1(сделай щелк мышью).
Отрезок ОА называют единичным отрезком.
Отложим отрезок АВ, равный отрезку ОА, он будет соответствовать числу 2, и так далее(сделай щелк мышью). Мы получили бесконечную шкалу. Ее называют координатным лучом. Числа 0, 1, 2, 3, …, соответствующие точкам О, А, В, С называют координатами этих точек.
Пишут: О(0), А(1), В(2).
О
0
А
1
В
С
2
3
Х
Натуральные числа. Понятие
Слайд 12
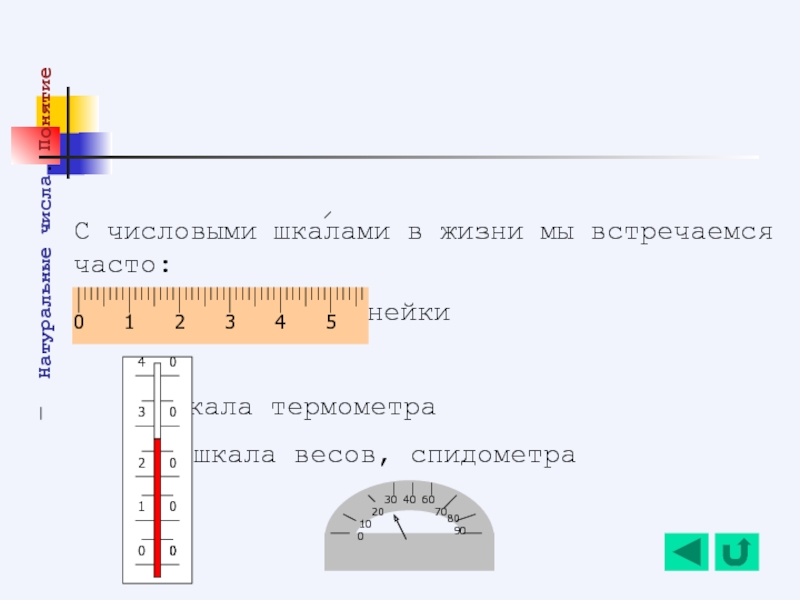
С числовыми шкалами в жизни мы встречаемся часто:
шкала линейки
шкала термометра
шкала весов, спидометра
Натуральные числа. Понятие
0
10
20
40
30
60
90
70
80
Слайд 13Натуральные числа. Понятие задачи
1. Определите, какой из этих рядов является рядом
2. Какое разложение соответствует числу 257?
3. Какое разложение соответствует числу 1058?
4. Какое число соответствует разложению 4*1000+5*100+3?
5. Если n=254, то чему равно n-1?
6. Если n=254, то чему равно n+1?
7. Если n=254, то чему равно n+3?
8. Если n=299, то чему равно n+1?
1,2,3,…
0,1,2,3,…
1,2,3
2*100+5+7*10
2*100+5*10+7
2*10+5*100+7*10
1*1000+5*10+8
1*1000+5*10+8*10
1*1000+5*100+8
4503
4350
4530
4053
253
255
257
300
254
254
254
2910
257
257
290
253
399
250
250
250
Слайд 14Натуральные числа. Округление
задачи
1. Округлите число 1058 до десятков.
2. Округлите число 1058
3. Округлите число 1058 до тысяч.
4. Округлите число 74337 до десятков тысяч.
5. Округлите число 74897 до тысяч.
6. 5630 - округлили число до десятков. Какое число могло быть первоначально?
1060
1058
1100
1050
1100
1000
10000
1050
1000
10000
1100
1050
74400
74400
5631
70000
74000
5638
74300
74300
5635
75000
75000
5628
Слайд 15Натуральные числа
Округление натуральных чисел
Если при подсчете количества или при измерениях точность
Например: при переписи населения установлено, что в городе проживает 20115 чел. Но количество людей постоянно изменяется (рождение, смерть, приезд, выезд). Поэтому говорят, что в городе проживает около 20000 чел.
В данном примере количество жителей указано округленным числом.
Алгоритм округления.
Определить разряд, до которого необходимо округлить число;
Если после разряда стоит цифра 0,1,2,3,4, то цифра этого разряда остается без изменения, младшие заменяются нулями;
Если после разряда стоит цифра 5,6,7,8,9, то цифра этого разряда увеличивается на 1, младшие заменяются нулями;
Например.
Необходимо округлить число 5394 до десятков. Получим 5390.
Необходимо округлить число 5394 до сотен. Получим 5400.
Необходимо округлить число 5394 до тысяч. Получим 5000.
Слайд 16Натуральные числа
Сравнение натуральных чисел
При счете натуральные числа называют по порядку 1,
Из двух натуральных чисел меньше то, которое при счете называют раньше, и больше то, которое при счете называют позже.
Например: число 4 меньше 7, а число 10 больше 7. Наименьшее натуральное число 1.
На координатном луче точка с меньшей координатой находится левее, а с большей – правее.
Например: точка А(4) лежит левее точки В(7), а точка С(10) правее точки В.
Для сравнения чисел используют специальные знаки < (меньше) и > (больше). Результат сравнения записывают в виде неравенства. Например 4<7, 10>7.
Можно использовать двойное неравенство,
так 7 больше 4 и меньше 10, то 4<7<10
Слайд 17Для сравнения чисел используют следующий алгоритм:
если в числах разное количество разрядов,
при равных количествах разрядов числа сравниваются поразрядно, начиная с наибольшего.
Например: 125 689 < 1285
56784<56984
95832>35632.
Сравнивают длины отрезков и записывают АВ>СD
Натуральные числа. Сравнение
Слайд 18Натуральные числа. Сравнение
Задачи
Какой знак сравнения нужно поставить вместо *?
23761 * 487
2. Какой знак сравнения нужно поставить вместо *?
23761 * 23987
3. Какое из двух чисел больше?
4. Какое число на координатном луче будет стоять правее?
или ; или
5. Какое число на координатном луче будет стоять левее?
или ; или
6. Как сравнить числа 56, 68, 45?
>
<
<
>
5689
5869
873
837
345
365
345
365
873
837
45<56<68
56<68>45
45>56>68
Слайд 19Натуральные числа
Числовые и буквенные выражения
При решении задач сначала записывают действия, а
Например: (18*3+15)-11
Число, полученное в результате выполнения всех действий, в числовом выражении называют значением этого выражения. (58)
Если в выражении заменить одно или несколько чисел буквой, то полученная запись называется буквенным выражением.
Например: (а*в+15)-с
Значение этого выражения будет зависеть от того, какими будут значения этих букв – переменных.
Например: выражение (2*а+5)-10
имеет значение 1 при а=3,
имеет значение 3 при а=4,
имеет значение 5 при а=5.
Слайд 20Уравнением называют равенство, содержащее букву (переменную), значение которой нужно найти.
Значение буквы
В уравнениях принято обозначать неизвестную величину переменной х.
Например: х+5=11 - уравнение, корнем которого является х=6. Проверим: 6+5=11, верно.
Покажем решение уравнения: (49-х)+24=63.
Решение (сопровождайте решение уравнения щелком мыши):
(49-х)+24=63;
найдем неизвестное слагаемое 49-х=63-24;
49-х=39;
найдем неизвестное вычитаемое х=49-39;
х=10.
корнем уравнения является х=10
Натуральные числа. Числовые и буквенные выражения
Слайд 21Натуральные числа.
Буквенные выражения
Задачи
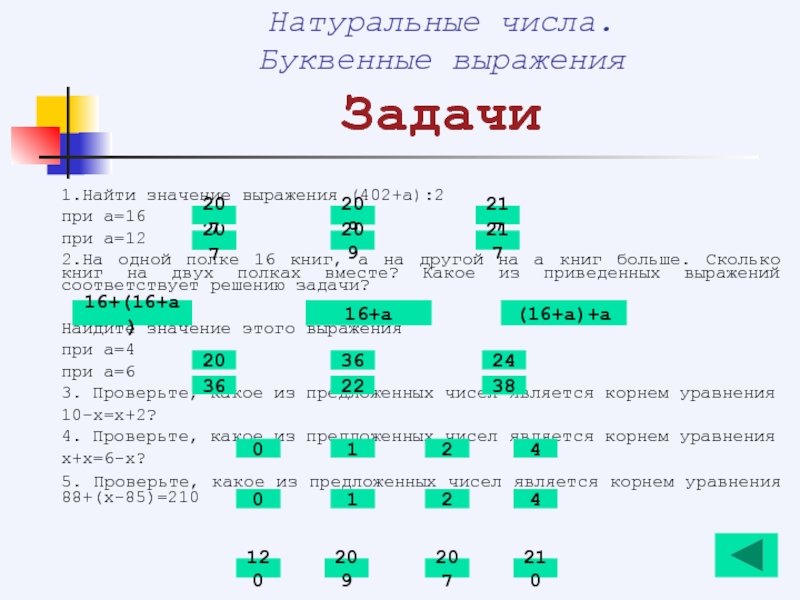
1.Найти значение выражения (402+а):2
при а=16
при а=12
2.На одной полке
Найдите значение этого выражения
при а=4
при а=6
3. Проверьте, какое из предложенных чисел является корнем уравнения
10-х=х+2?
4. Проверьте, какое из предложенных чисел является корнем уравнения
х+х=6-х?
5. Проверьте, какое из предложенных чисел является корнем уравнения 88+(х-85)=210
209
207
207
217
209
217
16+(16+а)
16+а
(16+а)+а
36
20
24
38
22
36
0
1
2
4
0
1
2
4
120
209
207
210
Слайд 22Натуральные числа
Сложение и вычитание натуральных чисел
Если прибавить к натуральному числу единицу,
Например, 6+1=7; 99+1=100.
Сложить числа 5 и 3 значит прибавить к числу 5 три раза единицу. Получим:
5+3 = 5+1+1+1 = 6+1+1 = 7+1 = 8.
Пишут короче: 5+3 = 8
Числа, которые складывают, называют слагаемыми; число, получающееся при сложении этих чисел, называют их суммой.
В записи 5+3=8 числа 5 и 3 – слагаемые, а число 8 – сумма.
Сложение чисел можно изобразить на координатном луче
(действия подтверждайте щелками мыши).
0
1
5
6
7
8
+3
Слайд 23Законы сложения
Переместительный. Сумма чисел не изменяется от перестановки слагаемых
а+в =
Например: 5+4 = 4+5 = 9
2. Сочетательный. Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме прибавить второе слагаемое.
а+(в+с) = (а+в)+с = а+в+с
Например: 2+(8+6)=16
(2+8)+6 = 16
3. От прибавления нуля число не изменяется а+0=а
Например: 5+0=5
Натуральные числа. Сложение чисел
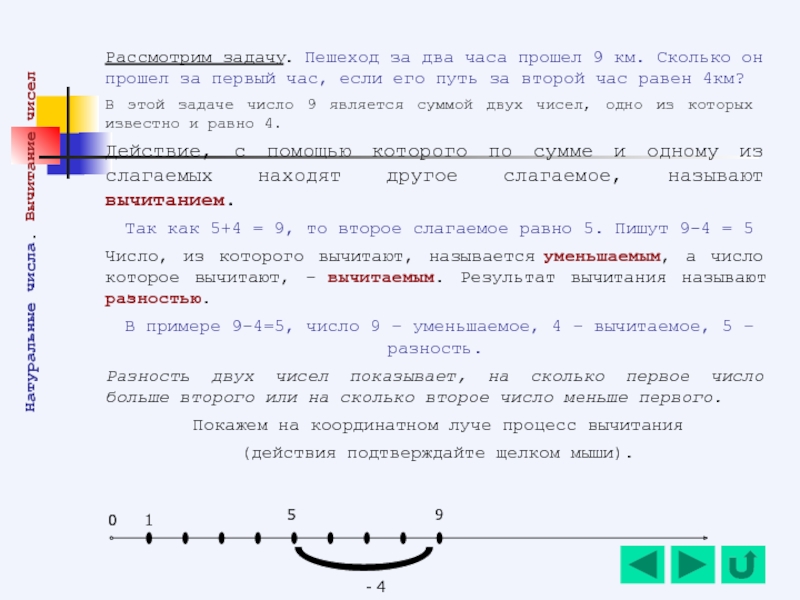
Слайд 24Рассмотрим задачу. Пешеход за два часа прошел 9 км. Сколько он
В этой задаче число 9 является суммой двух чисел, одно из которых известно и равно 4.
Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое, называют вычитанием.
Так как 5+4 = 9, то второе слагаемое равно 5. Пишут 9-4 = 5
Число, из которого вычитают, называется уменьшаемым, а число которое вычитают, - вычитаемым. Результат вычитания называют разностью.
В примере 9-4=5, число 9 – уменьшаемое, 4 – вычитаемое, 5 – разность.
Разность двух чисел показывает, на сколько первое число больше второго или на сколько второе число меньше первого.
Покажем на координатном луче процесс вычитания
(действия подтверждайте щелком мыши).
Натуральные числа. Вычитание чисел
Слайд 25Законы вычитания
Для того, чтобы вычесть сумму из числа, можно сначала вычесть
а-(в+с) = а-в-с
Например: 12-(3+2) = 12-5 = 7
(12-3)-2 = 9-2 = 7
2. Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое
(а+в)-с = (а-с)+в = а+(в-с)
Например: (6+3)-2 = 9-2 = 7
6+(3-2) = 6+1 = 7
(6-2)+3 = 4+3 = 7
3. Если из числа вычесть нуль, оно не изменится.
а+0 = а
4. Если из числа вычесть это же число, получится нуль.
а-а = 0
Натуральные числа. Вычитание чисел
Слайд 26Натуральные числа
Умножение и деление натуральных чисел
Сумму, в которой
Например, необходимо решить задачу.
В театре 20 рядов по 40 мест в каждом. Сколько мест в театре?
Чтобы решить задачу, необходимо
число 40 сложить 20 раз.
40+40+…+40=?.
Это действие можно заменить
умножением 40*20=800
Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m.
m*n = m+m+m+…+ m (n- раз)
Выражение m* n называется произведением
чисел m и n.
Числа m и n называются множителями.
20 рядов
40 мест в каждом
Слайд 27Законы умножения
1. Переместительный. Произведение двух чисел не изменяется при перестановке множителей.
а*в
Например 5*6=30 и 6*5=30
2. Сочетательный. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
а*(в*с) = (а*в)*с = а*в*с
Например: 5*(3*2) = 5*6 = 30;
(5*3)*2 = 15*2 = 30;
(5*2)*3 = 30.
3. Произведение любого числа на 1 равно самому числу.
а*1 = а
4. Произведение любого числа на нуль равно нулю.
а*0 = 0
Натуральные числа. Умножение чисел
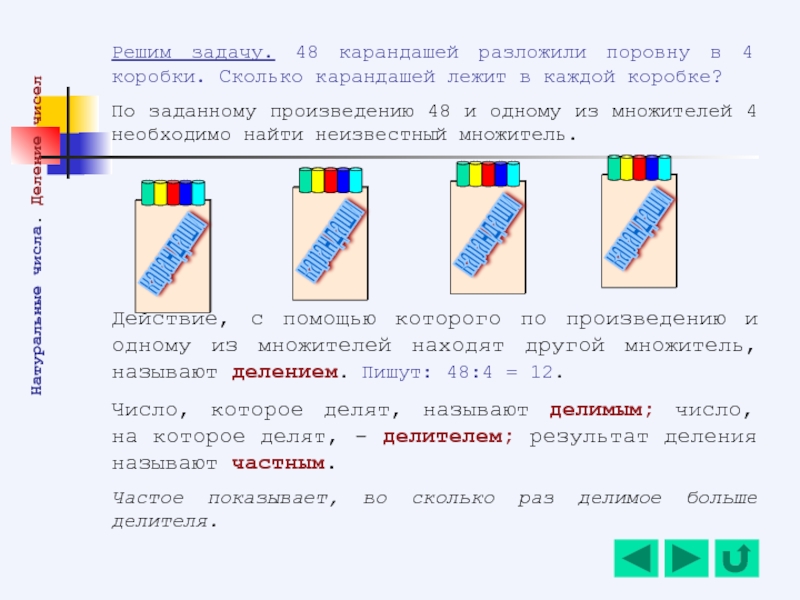
Слайд 28Решим задачу. 48 карандашей разложили поровну в 4 коробки. Сколько карандашей
По заданному произведению 48 и одному из множителей 4 необходимо найти неизвестный множитель.
Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением. Пишут: 48:4 = 12.
Число, которое делят, называют делимым; число, на которое делят, - делителем; результат деления называют частным.
Частое показывает, во сколько раз делимое больше делителя.
Натуральные числа. Деление чисел
Слайд 29Законы деления
1. Ни одно число нельзя делить на нуль
а:0
2. При делении
а:1 = а
3. При делении числа на себя получается единица
а:а = 1
4. При делении нуля на любое число получается нуль
0:а = 0
Натуральные числа. Деление чисел
Слайд 30Умножение и деление на разрядную единицу
Разрядной единицей называются числа, у которых
При умножении числа на разрядную единицу к числу дописывают нули столько раз, сколько нулей в разрядной единице.
Например: 548*100 = 54800, 2086*1000 = 2086000
При делении числа на разрядную единицу в числе вычеркивается столько нулей, сколько нулей в разрядной единице
Например: 54800:100 = 548,
54800:10 = 5480, 2086000:1000=2086,
2086000:100=20860,
2086000:10=208600.
Натуральные числа. Умножение и деление чисел
Слайд 31Натуральные числа. Умножение и деление чисел
Выражения (5+4)*3 и 5*3+4*3 имеют одно
Поэтому справедлив распределительный закон умножения относительно сложения.
Для того, чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и полученные произведения сложить.
(а+в)*с = ас+вс
Аналогичен распределительный закон умножения относительно вычитания.
Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе
(а-в)*с = ас-вс
Распределительное свойство умножения позволяет упрощать выражения вида: 3а+7а = (3+7)*а = 10а
26х-12х = (26-12)*х = 14х
Слайд 32Относительно деления тоже применяется распределительный закон.
Рассмотрим выражения: (2+4):2 и 2:2+4:2. Они
Аналогично выражения (12-6):3 и 12:3-6:3 имеют одно и то же значение. (12-6):3 = 6*3 = 2 и 12:3-6:3=4-2=2
Поэтому справедлив распределительный закон.
(а+в):с = а:с+в:с
(а-в):с = а:с-в:с
Распределительное свойство позволяет упрощать выражения вида: 3:а+12:а = (3+12):а = 15:а
26:х-12:х = (26-12):х = 14:х
Слайд 33Натуральные числа. Умножение и деление чисел
Произведение числа n на себя называется
n*n =n2
Например: 52 = 5*5 = 25
Произведение числа n на себя три раза называется кубом числа.
n*n*n =n3
Например: 53 = 5*5*5 = 125
Произведение числа n на себя m раз называется степенью числа.
n*n*n…*n =nm
Например: 24 = 2*2*2*2 = 16
25 = 2*2*2*2*2 = 32
Единица, возведенная в любую степень, равна 1:
12 = 1*1 = 1; 13 = 1*1*1 = 1; 15 = 1*1*1*1*1 = 1
Если в выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.
Например:
(4+3)2*52-83=72*25-512=49*25-512=1225-512=713
Слайд 34Натуральные числа.
Сложение и вычитание натуральных чисел
Задачи
1. Используя переместительное свойство сложения,
35+18+25
47+24+13
2. Используя сочетательное свойство сложения, вычислите:
99+(21+16)
25+(13+75)
3. Вычислите, выбирая удобный порядок действий:
(12+96)-36
37-(37-98)
4. Вычислите:
13+0
15-15
5. Вычислить значение выражения (35+а)-23
При а=0
При а=43
При а=15
6. Решите уравнения:
85-х=35 х+37=87
х-87=13 (х-35)+12=32
74
77
101
80
82
76
100
140
112
130
101
96
59
80
74
99
105
0
30
10
50
3
33
57
28
1
38
54
124
32
55
78
84
136
113
72
98
13
0
12
55
27
50
100
50
41
55
137
Слайд 35Натуральные числа.
Умножение и деление натуральных чисел
Задачи
Найдите значение выражения:
15+15+15+15
8+8+20+20
2. Выполните действия,
25*(4*12) 36*17+64*17
(13*2)*5 4*6*25
3. Укажите правильный ответ:
15*0= 15:15=
15:0= 0:15=
4. Найдите значение выражения:
(а-12)*8 при а=22
(а+5):3 при а=28
5. Решите уравнение:
26х=260 (12+в)*2=84
Х:25=4 (95-х):5=15
6. Какое из чисел при делении
на 3 дает остаток 2?
на 5 дает остаток 3?
30
16
100
13
15
нельзя
15
0
53
24
21
54
45
42
15
10
21
6
56
60
1200
130
0
0
1
0
80
11
10
100
30
20
20
18
1700
600
170
1600
Слайд 36Натуральные числа.
Умножение и деление натуральных чисел на разрядную единицу
Задачи
1. Найти
256*10=
256*100=
256*1000=
2. Найти значение выражения:
56000:10=
56000:100=
56000:1000=
3. Найти значение выражения:
389*1000:100=
56200:100*100=
4. Выполните действия:
12*60= 33000:30=
25*400= 32000:160=
5. Решите уравнения:
3*х=30 х:7=30
3*(х-1)=30 5*(х-1)=1250
2810
25600
256
2560
25600
256000
5600
560
56
3890
56200
720
10000
1100
200
210
251
10
11
2547
2560
2560
25600
2369
256
56
56000
56
560000
560
5600
560
5600
56000
389
38900
389000
5620
562
562000
72
100000
110
20
2100
2510
10
100
Слайд 37Представьте в виде произведения выражение:
23а+37а= 85в-70в=
49х+х= 32с-с=
2. Вычислите удобным способом:
38*48+38*52= (21)*7=
87:15-57:15= 19*5=
3. Найдите значение выражения:
6в+5в при в=3
13х-8х при х=5
4. Раскройте скобки:
2*(х+3)= (а-20):5=
3*(12-х)= (3+2х-х)*7=
5. Решите уравнения:
4х+7х=33 3х+2х-8=32
31х-х=60 15х-5х-8=92
Натуральные числа.
Распределительный закон умножения
Задачи
60a
60+2a
49x
15-b
32c
3850
3
133
101
25
10
11
20
5
12
2x+3
36-x
а:5-20
21+x
50x
31c
15b
36-3x
2x+6
а:5-4
21+7x
147
95
2
3800
3
2
8
10
33
25
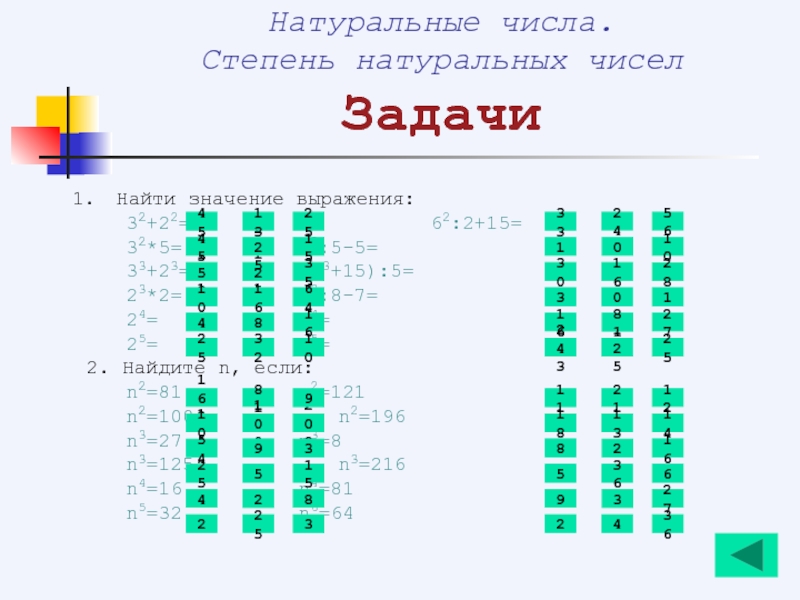
Слайд 38Найти значение выражения:
32+22=
32*5= 52:5-5=
33+23= (53+15):5=
23*2= 43:8-7=
24= 34=
25= 35=
2. Найдите n, если:
n2=81 n2=121
n2=100 n2=196
n3=27 n3=8
n3=125 n3=216
n4=16 n4=81
n5=32 n6=64
Натуральные числа.
Степень натуральных чисел
Задачи
45
25
15
158
125
225
10
64
4
8
25
10
24
56
1
10
30
16
3
0
16
27
125
25
162
81
100
200
54
9
25
15
4
8
25
3
21
12
18
13
8
16
5
36
9
27
4
36
13
45
35
16
16
32
33
0
28
1
81
243
11
14
2
6
3
2
9
10
3
5
2
2
Слайд 40Меры измерения величин
Меры времени
Время измеряется сутками, часами, минутами, секундами.
1 сутки =
1 час = 60 минут
1 минута = 60 секунд
1 секунда = 60 миллисекунд
Например: 2 суток = 48 часов = 48*60 минут = 2880 секунд
6 часов = 6*60 минут = 360 минут
360 минут = 360*60 секунд = 21600 секунд
Слайд 41Например: 6 часов = суток = 0,25 суток,
30 минут = часа = 0,5 часа; 30 секунд = минут =0,5 минут;
15 минут = часа = 0,25 часа; 15 секунд = минут = 0,25 минут.
Меры измерения величин. Меры времени.
Можно сравнивать и части, так
1 час = суток
1 минута = часа
1 секунда = минуты
1 миллисекунда = секунды
Слайд 42Меры измерения времени
Задачи
Выразите в часах: 2 суток 3ч.
Выразите в часах: 540
Выразите в часах: 14400с.
Выразите в минутах и секундах: 172с.
Выразите в часах и минутах: 150м.
Сравните: 116мин и 2ч.
Сравните: 72ч и 3сут.
Вычислите: 5ч36мин+10ч54мин.
Выразите в часах: 360 мин.
Выразите в сутках: 36ч.
26
48
51
54
8
9
36
21
4
2мин86с
3мин
2мин52с
>
<
<
=
15ч90мин
17ч
16ч30мин
232м
2ч30с
2ч30м
1ч
60ч
6ч
1сут6ч
3ч
1сут12ч
Слайд 43Меры измерения величин
Меры длины
Расстояние измеряется в
километрах (км),
дециметрах (дм), сантиметрах (см),
миллиметрах (мм)
1 сантиметр = 10 мм
1 дециметр = 10 см = 100 мм
1 метр = 10 дм =100 см = 1000 мм
1 километр = 1 000 м = 10 000 дм = 100 000 см = 1 000 000 мм
Например: 2 км = 2000 м; 5000 м = 5 км;
200 м = 20000 см; 3600 см = 36 м;
26 дм = 260 см; 50 см = 5 дм;
50 см = 500 мм; 2800 мм = 280 см.
Слайд 44Меры измерения величин. Меры длины
Можно сравнивать и части, так
1 метр =
1 дециметр = 0,1 м = 0,0001 км
1 сантиметр = 0,1 дм = 0,01 м
1 миллиметр = 0,1 см = 0,01 дм = 0,001 м
Например: 5 м = 0,005 км; 36000м = 36 км;
20 см = 2 дм = 0,2 м; 36м = 0,036 км;
300 см = 30 дм = 3 м; 580 см = 58 дм =5,8 м;
500 мм = 50 см = 5 дм = 0,5 м 800 м = 0,8 км.
Слайд 45Меры измерения длины
Задачи
Выразите в сантиметрах 3м5см.
Выразите в метрах 40км3м.
Выразите в километрах
Выразите в дециметрах: 680см.
Выразите в миллиметрах 548см.
Сравните 3 дм и 23 см.
Сравните 1км и 1002м.
Вычислите 2км 300м + 1200м.
Выразите в метрах 2км300м.
Выразите в сантиметрах 500мм.
35
350
305
4030
4003
40003
56км0м
5км6м
5км 600м
6дм8см
6дм80см
68дм
<
>
>
<
2км 1500м
2км4200м
3км500м
54800
54,8
5480
20300м
23000м
2300м
0,5см
5см
50см
Слайд 46Меры измерения величин
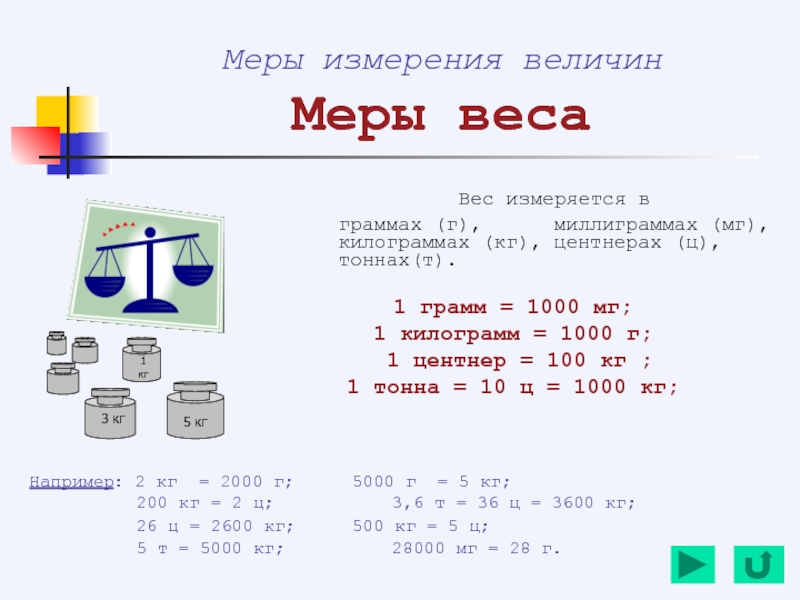
Меры веса
Вес измеряется в
граммах (г), миллиграммах
1 грамм = 1000 мг;
1 килограмм = 1000 г;
1 центнер = 100 кг ;
1 тонна = 10 ц = 1000 кг;
Например: 2 кг = 2000 г; 5000 г = 5 кг;
200 кг = 2 ц; 3,6 т = 36 ц = 3600 кг;
26 ц = 2600 кг; 500 кг = 5 ц;
5 т = 5000 кг; 28000 мг = 28 г.
Слайд 47Например: 5 кг = 0,05ц = 0,005 т;
200 г = 0,2 кг; 36 ц = 3,6 т;
300 ц = 30 т; 580 кг = 5,8 ц =0,58 т;
5000 мг = 5 г = 0,005 кг; 800 кг = 0,8 т.
Меры измерения величин. Меры веса.
Можно сравнивать и части, так
1 миллиграмм = 0,001 г
1 грамм = 0,001 кг
1 килограмм = 0,01 ц = 0,001 т
1 центнер = 0,1 т
Слайд 48Меры измерения веса
Задачи
Сколько килограммов в 40ц?
Сколько центнеров в 800кг?
Выразите в граммах
Выразите в тоннах 1020ц.
Выразите в тоннах и центнерах 653ц.
Сравните 3ц и 289кг.
Сравните 10ц и 1т.
Вычислите 15т354кг – 4т 876кг.
Выразите в килограммах 1200г.
Выразите в тоннах 1200кг.
400
4
4000
8000
80
8
1320
132
13200
10,2
10200
102
<
>
>
=
10т522кг
11т522кг
10т478кг
6т53ц
653т
65т3ц
120кг
12кг
1кг200г
120т
12т
1т200кг
<
=
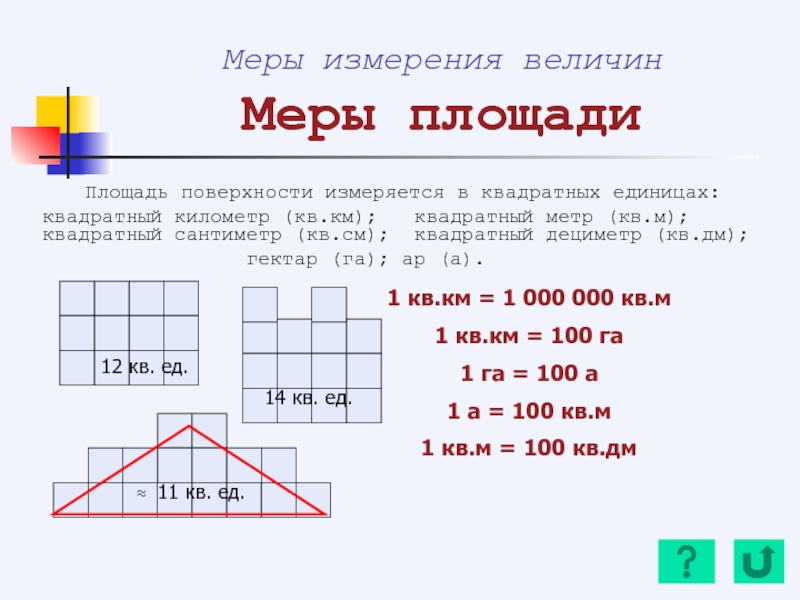
Слайд 49Меры измерения величин
Меры площади
Площадь поверхности измеряется в квадратных единицах:
квадратный километр (кв.км);
гектар (га); ар (а).
1 кв.км = 1 000 000 кв.м
1 кв.км = 100 га
1 га = 100 а
1 а = 100 кв.м
1 кв.м = 100 кв.дм
Слайд 50Меры измерения площади
Задачи
Выразите 36дм2 в см2.
Выразите 64000дм2 в м2.
Выразите 24а в
Выразите 5га в м2.
Выразите 600м2 в арах.
Выразите 13га в арах.
Сравните 23га и 2300а.
Сравните 7а и 700м2.
Сравните 5га и 50000м2.
Сравните 2800м2 и 28га.
36
360
3600
6400
64
640
240
24
2400
500
50
50000
=
60
600
6
=
>
<
13
130
1300
>
<
=
>
<
=
>
<
Слайд 51Меры измерения величин
Меры объема
Объем измеряется в кубических единицах:
кубический метр (куб.км); кубический
литр (л); декалитр (дкл); гектолитр (гл).
1 куб.м = 1 000 000 куб.см
1 куб.см = 1000 куб.мм
1 гл = 100 л
1 дкл = 10 л
1 л = 1 куб.дм
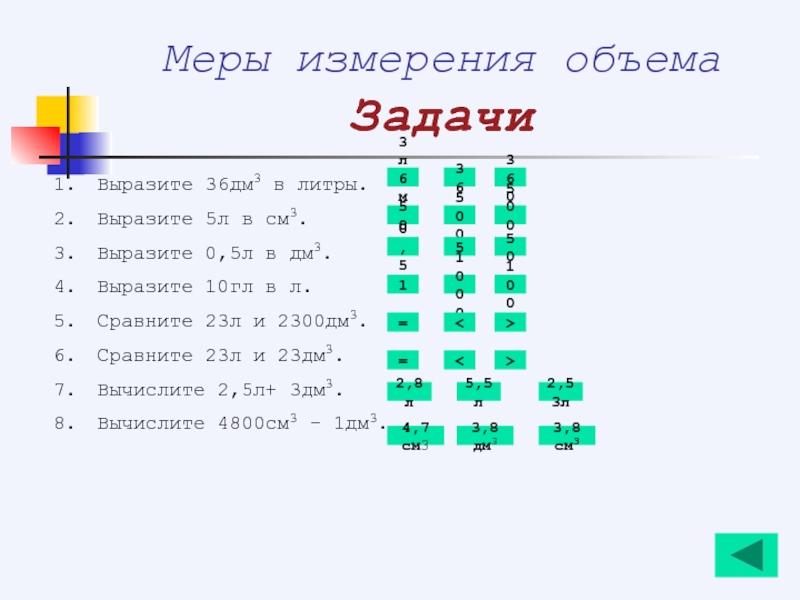
Слайд 52Меры измерения объема
Задачи
Выразите 36дм3 в литры.
Выразите 5л в см3.
Выразите 0,5л в
Выразите 10гл в л.
Сравните 23л и 2300дм3.
Сравните 23л и 23дм3.
Вычислите 2,5л+ 3дм3.
Вычислите 4800см3 - 1дм3.
3л6мл
360
36
50
500
5000
5
50
0,5
1
100
1000
=
>
<
>
<
=
2,8л
2,53л
5,5л
4,7см3
3,8см3
3,8дм3
Слайд 53 Решение уравнений
Левая часть уравнения
представляет собой сумму
Левая часть уравнения
представляет
Левая часть уравнения
представляет собой произведение
Левая часть уравнения
представляет собой частное
Другие уравнения
Понятие
выход
Слайд 54Решение уравнений
Понятие
Уравнением называют равенство, содержащее букву (переменную), значение которой нужно
Значение буквы (переменной), при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение – значит найти все его корни или убедиться, что таковых нет.
В уравнениях принято обозначать неизвестную величину переменными х, y, z.
Например: х+5=11 - уравнение, корнем которого является х=6. Проверим: 6+5=11, верно.
Слайд 55Решение уравнений. Понятие
Задачи
Проверьте, является ли корнем уравнения х-20=5
число 3?
число 5?
число
2. Какое из чисел является корнем уравнения (х-6)*(7-х)=0?
Сколько корней может быть у уравнения х-20=5?
Сколько корней может быть у уравнения (х-6)*(7-х)=0?
Сколько корней может быть у уравнения 35:0=0?
является
нет
является
нет
нет
да
10
6
0
7
2
1
Нет корней
2
1
1
Нет корней
2
Нет корней
Слайд 56Решение уравнений
Левая часть уравнения
представляет собой сумму
Рассмотрим уравнения, в которых
Расположение слагаемых не важно согласно переместительному закону сложения 35+х = х+35. Для нахождения неизвестного рассуждать нужно так:
Как найти неизвестное слагаемое?
Нужно от известной суммы вычесть известное слагаемое.
Например: х + 35 = 75,
Сопровождайте демонстрацию решения уравнения щелком мыши.
Как найти неизвестное слагаемое х?
От известной суммы 75 нужно вычесть известное слагаемое 35 х = 75 – 35;
Х = 40.
Сделаем проверку.
Проверка: 40 + 35 = 75;
75 = 75, верно.
Ответ: 40.
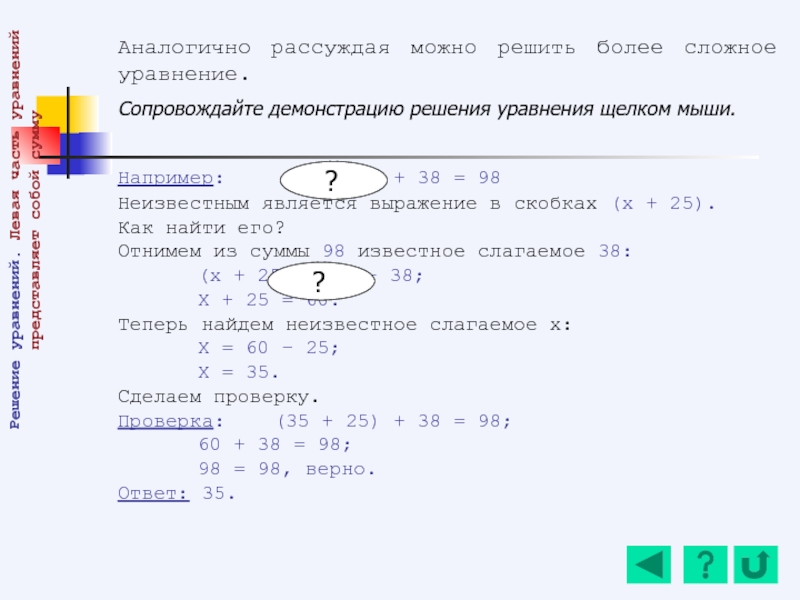
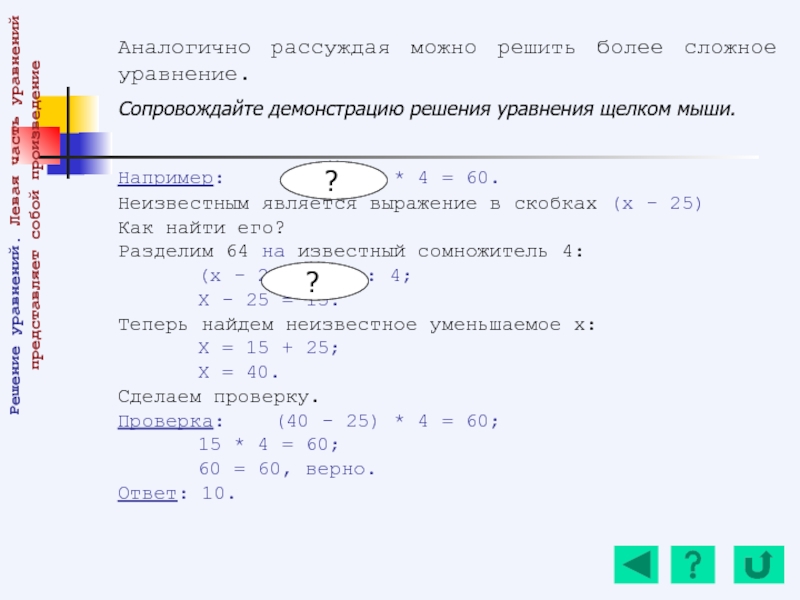
Слайд 57Аналогично рассуждая можно решить более сложное уравнение.
Сопровождайте демонстрацию решения уравнения
Например: (х + 25) + 38 = 98
Неизвестным является выражение в скобках (х + 25).
Как найти его?
Отнимем из суммы 98 известное слагаемое 38:
(х + 25) = 98 – 38;
Х + 25 = 60.
Теперь найдем неизвестное слагаемое х:
Х = 60 – 25;
Х = 35.
Сделаем проверку.
Проверка: (35 + 25) + 38 = 98;
60 + 38 = 98;
98 = 98, верно.
Ответ: 35.
Решение уравнений. Левая часть уравнений представляет собой сумму
Слайд 58Левая часть уравнения представляет собой сумму
Задачи
Чем в уравнении х+46=500 является неизвестное?
Решите
Решите уравнение 2+20+х=42.
Решите уравнение х+24+76=120.
Решите уравнение(х+15)+20=65.
Решите уравнение 60+(15+х)=120.
сумма
слагаемое
1000
752
725
11
20
62
140
20
68
55
30
70
195
45
55
разность
Слайд 59Решение уравнений
Левая часть уравнения
представляет собой разность
Рассмотрим уравнения, в которых
В процессе вычитания 25-5=20, число из которого вычитают называется уменьшаемым (25), число которое вычитают называется вычитаемым (5), результат вычитания называется разностью (20).
Поэтому при решении уравнения необходимо выяснить чем является неизвестное: уменьшаемым или вычитаемым. В зависимости от этого рассуждают следующим образом.
Слайд 60Например: х - 35 = 65.
Сопровождайте демонстрацию решения уравнения
Как найти неизвестное уменьшаемое х?
К известной разности 65 нужно прибавить известное вычитаемое 35.
х = 65 + 35;
Х = 100.
Сделаем проверку.
Проверка: 100 - 35 = 65;
65 = 65, верно.
Ответ: 100.
Если неизвестным является уменьшаемое (х-35=65), то к известной разности (65) нужно прибавить известное вычитаемое (35).
Решение уравнений. Левая часть уравнений представляет собой разность
Слайд 61Например: 75 - х = 65.
Сопровождайте демонстрацию решения уравнения
Как найти неизвестное вычитаемое х?
Из известного уменьшаемого 75 нужно вычесть известную разность 35:
х = 75 - 65;
Х = 10.
Сделаем проверку.
Проверка: 75 - 10 = 65;
65 = 65, верно.
Ответ: 10.
Если неизвестным является вычитаемое (75-х=65), то из известного уменьшаемого (75) нужно вычесть известную разность (65).
Решение уравнений. Левая часть уравнений представляет собой разность.
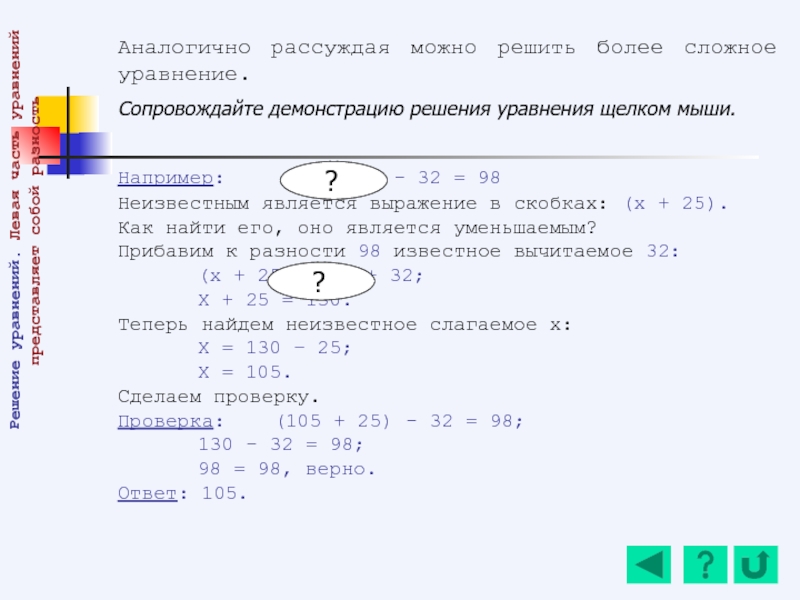
Слайд 62Аналогично рассуждая можно решить более сложное уравнение.
Сопровождайте демонстрацию решения уравнения
Например: (х + 25) - 32 = 98
Неизвестным является выражение в скобках: (х + 25).
Как найти его, оно является уменьшаемым?
Прибавим к разности 98 известное вычитаемое 32:
(х + 25) = 98 + 32;
Х + 25 = 130.
Теперь найдем неизвестное слагаемое х:
Х = 130 – 25;
Х = 105.
Сделаем проверку.
Проверка: (105 + 25) - 32 = 98;
130 - 32 = 98;
98 = 98, верно.
Ответ: 105.
Решение уравнений. Левая часть уравнений представляет собой разность
Слайд 63Левая часть уравнения представляет собой разность
Задачи
Чем в уравнении х-15=65 является неизвестное?
Чем
Решите уравнение х-15=65.
Решите уравнение 65-х=25.
Решите уравнение( х+15)-30=80.
Решите уравнение 95-(х+43)=45.
вычитаемое
уменьшаемое
разность
уменьшаемое
вычитаемое
разность
50
80
40
50
40
80
15
95
125
93
2
97
Слайд 64Решение уравнений
Левая часть уравнения
представляет собой произведение
Рассмотрим уравнения, в которых
Расположение сомножителей не важно согласно переместительному закону умножения 3*х = х*3). Для нахождения неизвестного сомножителя рассуждать нужно так:
Как найти неизвестный сомножитель?
Нужно известное произведение разделить на известный сомножитель.
Например: 3 * х = 36.
Сопровождайте демонстрацию решения уравнения щелком мыши.
Как найти неизвестный сомножитель х?
Известное произведение 36 нужно разделить на известный сомножитель 3:
х = 36 : 3;
Х = 12.
Сделаем проверку.
Проверка: 3 * 12 = 36;
36 = 36, верно.
Ответ: 12.
Слайд 65Аналогично рассуждая можно решить более сложное уравнение.
Сопровождайте демонстрацию решения уравнения
Например: (х - 25) * 4 = 60.
Неизвестным является выражение в скобках (х - 25)
Как найти его?
Разделим 64 на известный сомножитель 4:
(х - 25) = 60 : 4;
Х - 25 = 15.
Теперь найдем неизвестное уменьшаемое х:
Х = 15 + 25;
Х = 40.
Сделаем проверку.
Проверка: (40 - 25) * 4 = 60;
15 * 4 = 60;
60 = 60, верно.
Ответ: 10.
Решение уравнений. Левая часть уравнений представляет собой произведение
Слайд 66Левая часть уравнения представляет собой произведение
Задачи
Чем в уравнении х*15=135 является неизвестное?
Решить
Решить уравнение (х+36)*2=120.
Решить уравнение 8*(45-х)=160.
Решить уравнение 2х+5х=49.
Решить уравнение 3х+68+2х+32=200.
делимое
сомножитель
произведение
2025
9
105
276
24
204
1235
25
65
56
7
42
95
20
305
Слайд 67Решение уравнений
Левая часть уравнения
представляет собой частное
Рассмотрим уравнения, в которых
В процессе деления 75:3=25, число которое делится называется делимым (75), число на которое делят называется делителем (3), результат деления называется частным (25).
Поэтому при решении уравнения необходимо выяснить чем является неизвестное: делимым или делителем. В зависимости от этого рассуждают следующим образом.
Слайд 68Например: х : 3 = 12.
Сопровождайте демонстрацию решения уравнения
Как найти неизвестное делимое х?
Известный делитель 3 нужно умножить на известное частное 12:
х = 12 * 3;
Х = 36.
Сделаем проверку.
Проверка: 36 : 3 = 12;
12 = 12, верно.
Ответ: 36.
Если неизвестным является делимое(х:3=12), то известное частное (12) нужно умножить на известный делитель (3).
Решение уравнений. Левая часть уравнений представляет собой частное
Слайд 69Например: 75 : х = 5.
Сопровождайте демонстрацию решения уравнения
Как найти неизвестный делитель х?
Известное делимое 75 нужно разделить на известное частное 5:
х = 75 : 5;
Х = 25.
Сделаем проверку.
Проверка: 75 : 25 = 5;
5 = 5, верно.
Ответ: 25.
Если неизвестным является делитель (75:х=5), то известное делимое (75) нужно разделить на известное частное (5).
Решение уравнений. Левая часть уравнений представляет собой частное
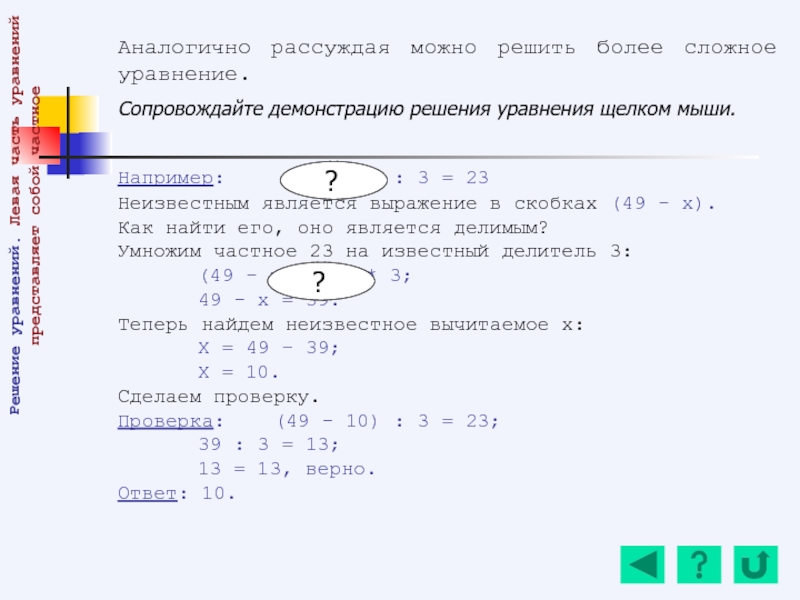
Слайд 70Аналогично рассуждая можно решить более сложное уравнение.
Сопровождайте демонстрацию решения уравнения
Например: (49 - х) : 3 = 23
Неизвестным является выражение в скобках (49 - х).
Как найти его, оно является делимым?
Умножим частное 23 на известный делитель 3:
(49 - х) = 23 * 3;
49 - х = 39.
Теперь найдем неизвестное вычитаемое х:
Х = 49 – 39;
Х = 10.
Сделаем проверку.
Проверка: (49 - 10) : 3 = 23;
39 : 3 = 13;
13 = 13, верно.
Ответ: 10.
Решение уравнений. Левая часть уравнений представляет собой частное
Слайд 71Левая часть уравнения представляет собой частное.
Задачи.
1. Чем в уравнении х:15=9 является
2. Чем в уравнении 135:х=9 является неизвестное?
3. Решите уравнение х:18=9.
4. Решите уравнение 210:х=7.
5. Решите уравнение 15:х=0.
6. Решите уравнение х:37=0.
7. Решите уравнение (х-25):4=100.
8. Решите уравнение 36:(48-х)=9.
делитель
делимое
частное
делимое
делитель
частное
2
162
27
1470
30
3
Нет решения
15
0
0
15
Нет решения
0
375
50
52
44
276
Слайд 72Если в уравнении присутствует выражение с переменными, то сначала необходимо выполнить
Например: (3х + 5х) * 3 = 72.
Сопровождайте демонстрацию решения уравнения щелком мыши.
Выполним действия в скобках:
8х * 3 = 72.
Применим переместительный закон умножения:
8*3*х = 72;
24х = 72.
Найдем неизвестный сомножитель:
х = 72:24;
Х = 3;
Сделаем проверку.
Проверка: (3*3 + 5*3) * 3 = 72;
(9 + 15) * 3 = 72;
24 * 3 = 72;
72 = 72, верно.
Ответ: 3.
Решение уравнений
Другие виды уравнений
Слайд 73Есть уравнения, левая часть которых представляют собой произведение, а правая часть
Тогда рассуждают следующим образом:
Произведение равно нулю в том случае, если один или оба сомножителя равны нулю.
Например: х * 25 = 0.
Произведение равно нулю, то каждый из сомножителей может быть равен нулю.
25≠0, значит х=0.
Проверка: 0*25=0;
0=0, верно.
Ответ: 0.
Решение уравнений. Другие виды уравнений
Слайд 74Рассмотрим более сложные уравнения:
Решить уравнение:(х-5)*63 = 0.
Решение:
(х-5)*63 = 0;
Х=5.
Проверка: (5-5)*63=0;
0*63=0;
0=0, верно.
Ответ: 5.
2. Решить уравнение: х * (1 - х) = 0.
Решение:
х * (1 - х) = 0;
Х=0 или 1 - х = 0;
тогда х=0 или х=1.
Проверка: подставим х=0: подставим х=1:
0* (1 - 0) = 0; 1 * (1-1) = 0;
0*1 = 0; 1 * 0 = 0;
0=0, верно. 0=0, верно.
Ответ: 0, 1.
В данном уравнении мы получили два решения.
Решение уравнений. Другие виды уравнений
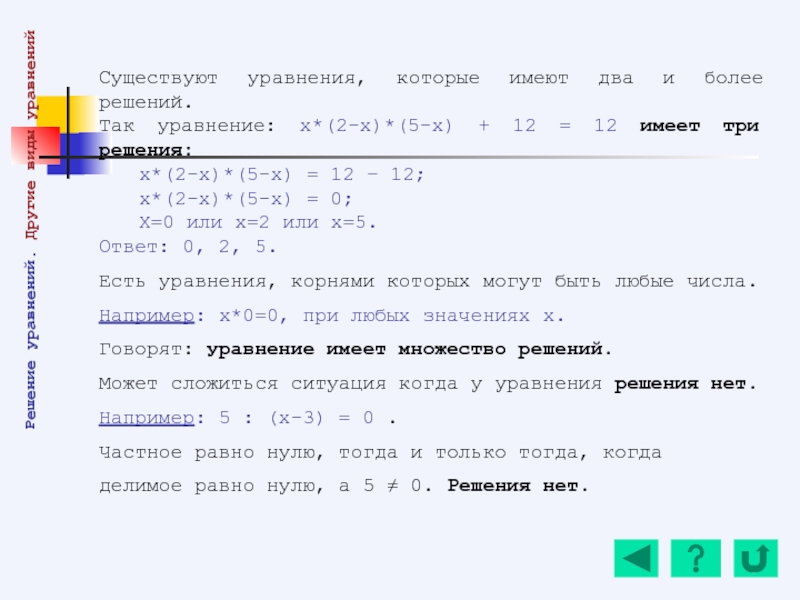
Слайд 75Существуют уравнения, которые имеют два и более решений.
Так уравнение: х*(2-х)*(5-х) +
х*(2-х)*(5-х) = 12 – 12;
х*(2-х)*(5-х) = 0;
Х=0 или х=2 или х=5.
Ответ: 0, 2, 5.
Есть уравнения, корнями которых могут быть любые числа.
Например: х*0=0, при любых значениях х.
Говорят: уравнение имеет множество решений.
Может сложиться ситуация когда у уравнения решения нет.
Например: 5 : (х-3) = 0 .
Частное равно нулю, тогда и только тогда, когда
делимое равно нулю, а 5 ≠ 0. Решения нет.
Решение уравнений. Другие виды уравнений
Слайд 76Другие виды уравнений
Задачи
Сколько корней будут иметь следующие уравнения:
(х-4)*(5-х)=0?
х:38=0?
38:х=0?
х:х=0?
х2=0?
0*х=0?
2. Решите уравнение (х-4)*(5-х)=0.
3. Решите уравнение (2х+3х-15)*(х-1)=0.
4. Решите уравнение (3х-39)*(х-41)*(125-5х)=0.
5. Решите уравнение х2=0.
один
два
Нет корней
один
два
Нет корней
один
Нет корней
Нет корней
три
три
два
три
один
три
Нет корней
один
три
один
Нет корней
три
два
два
два
Х=5
Х=4 или Х=5
Х=4
Х=3
Х=3 или Х=1
Х=4 или Х=1
Решений нет
Х=13, Х=41 или Х=25
Х=4 или Х=1
Х=0
Решений нет
Множество решений
Множество решений
Множество решений
Множество решений
Множество решений
Множество решений
Множество решений
один
Нет корней
три
два
Множество решений
Слайд 80Обыкновенные дроби
Понятие
Сравнение обыкновенных дробей
Сложение и вычитание обыкновенных дробей
Смешанные числа. Действия над
выход
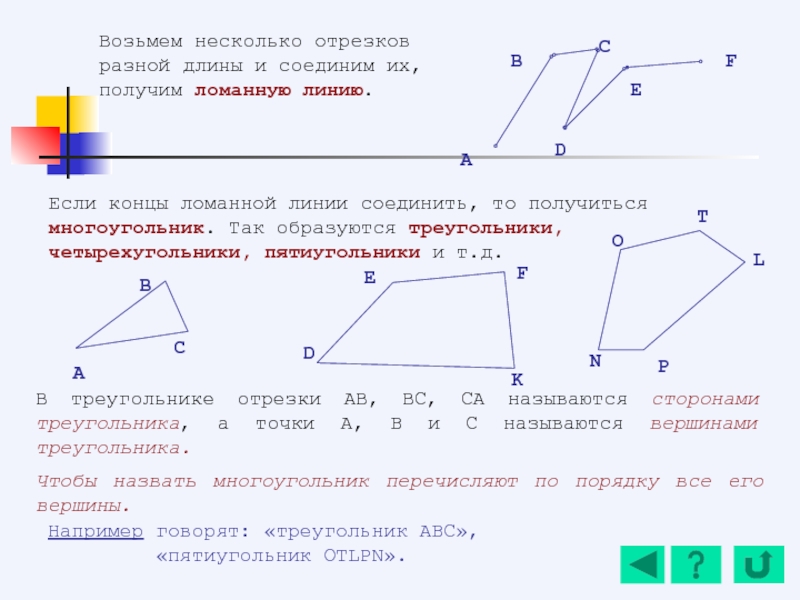
Слайд 81Возьмем яблоко и разрежем его на 4 равные части. Эти равные
Себе возьмем одну долю. Так как яблоко
разрезали на 4 долей, то мы взяли
«одну четвертую часть яблока».
Пишут так: .
Если мы возьмем 3 доли, то скажем
«мы взяли три четвертые яблока» и
запишем: .
Записи вида: , называют обыкновенными дробями.
Обыкновенные дроби
Понятие
Слайд 82Рассмотрим еще пример: торт разрезали
на 8 долей, возьмем 5.
Взяли
Дроби можно изображать на координатном луче.
Возьмем на луче отрезок ОА, разделим его на 6 равных отрезков и отметим , , , И Т.Д.
Причем, число, которое определяет на сколько частей разделили называется знаменателем (пишут его под дробной чертой), а число, которое показывает сколько взяли – числителем (пишут его над дробной чертой).
Обыкновенные дроби. Понятие
Слайд 83Если яблоко разрезали на 4 части а взяли 3,
то в
меньше знаменателя 4, такие дроби называются
правильными.
Но если взять 4 части или больше (5, 6), то в полученных дробях
, , числитель
больше знаменателя.
Такие дроби называются
неправильными.
Обыкновенные дроби. Понятие
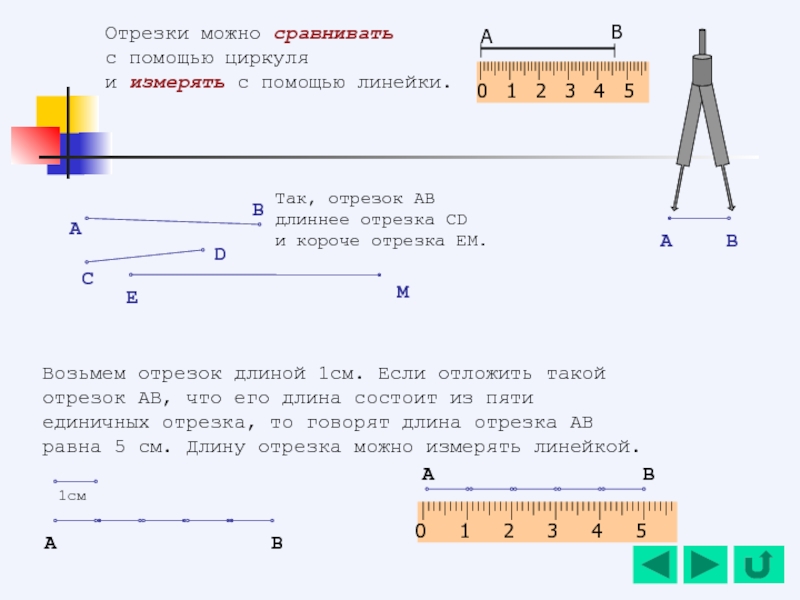
Слайд 84Разделим 3 одинаковых яблока между четырьмя детьми. Число 3 не делится
Поэтому разделим каждое яблоко
на 4 части и дадим каждому
по одной части от каждого
яблока.
Каждая часть – это яблока, а три такие части - яблока. Значит, каждый получил .
Дробь получилась при делении 3 яблок на 4 равные части: .
Поэтому дробную черту можно понимать как знак
деления
Обыкновенные дроби. Понятие
Слайд 85С помощью дробей можно записывать результат деления двух любых натуральных чисел.
Например:
И наоборот.
Запишем число 3 в виде дроби со знаменателем 5. Какое число делится нацело на 5, чтобы получилось 3? 15.
Получим:
Любое натуральное число можно записать в виде дроби с любым натуральным показателем.
Числитель этой дроби будет равен произведению числа на этот знаменатель.
Закон (а+в):с=а:с+в:с можно записать в виде дроби:
Обыкновенные дроби. Понятие
Слайд 86Какая часть круга заштрихована?
Какая часть круга заштрихована?
Дробь с числителем 7 и
Какая из данных дробей является правильной?
Представьте число 5 обыкновенной дробью со знаменателем 12.
Разделите на 6 человек 3 буханки хлеба.
Каждый получит по …
Обыкновенные дроби.
Понятие
Задачи
Внимание!
При ответе указатель мыши нужно установить на кнопку так, чтобы она изменила свое изображение на
Слайд 87Обыкновенные дроби
Сравнение дробей
Разделим одно яблоко на 4 равные части, возьмем две.
Две
пол яблока, что соответствует дроби .
Говорят, что дроби и равны
и пишут:
Сравните и . Они равны.
Сравните и .
Они тоже равны.
=
=
=
Слайд 88Обыкновенные дроби. Сравнение дробей
На координатном луче равные дроби соответствуют одной и
Будем сравнивать дроби с равными знаменателями.
Пирог разрезали на 8 частей. Гости съели , - осталось.
Что больше?
Из двух дробей с одинаковым знаменателем меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
На координатном луче правее находится дробь, которая больше.
<
1
Слайд 89Сравните дроби
и .
и .
и .
и .
и .
и .
Обыкновенные дроби.
Сравнение
Задачи
<
>
=
<
=
=
<
>
<
>
=
=
>
>
>
=
<
<
=
<
>
Слайд 90Обыкновенные дроби
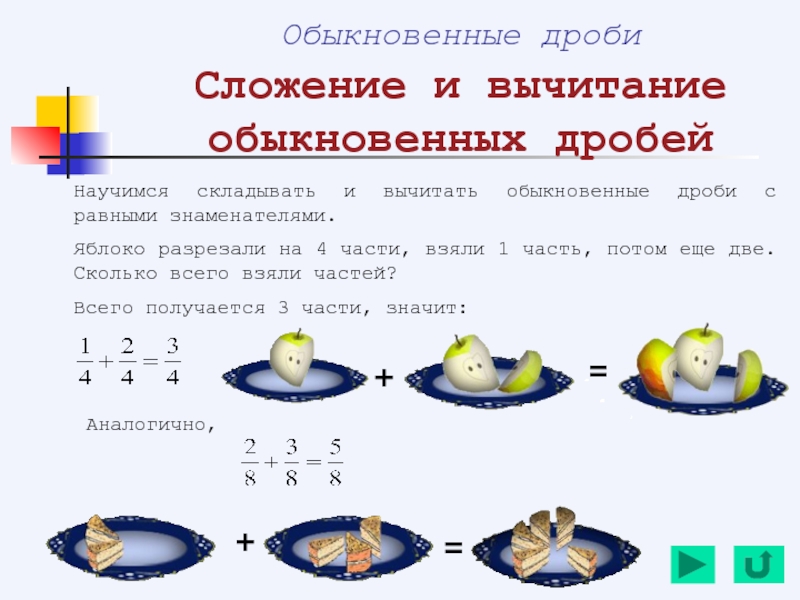
Сложение и вычитание обыкновенных дробей
Научимся складывать и вычитать обыкновенные
Яблоко разрезали на 4 части, взяли 1 часть, потом еще две. Сколько всего взяли частей?
Всего получается 3 части, значит:
Аналогично,
+
=
+
=
Слайд 91Обыкновенные дроби. Сложение и вычитание обыкновенных дробей
При сложении дробей с одинаковыми
Научимся вычитать дроби с одинаковыми знаменателями.
На тарелку положили 5 частей торта, разрезанного на 8 частей. Гости съели 2 части. Сколько осталось?
Осталось 3 доли.
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же.
-
=
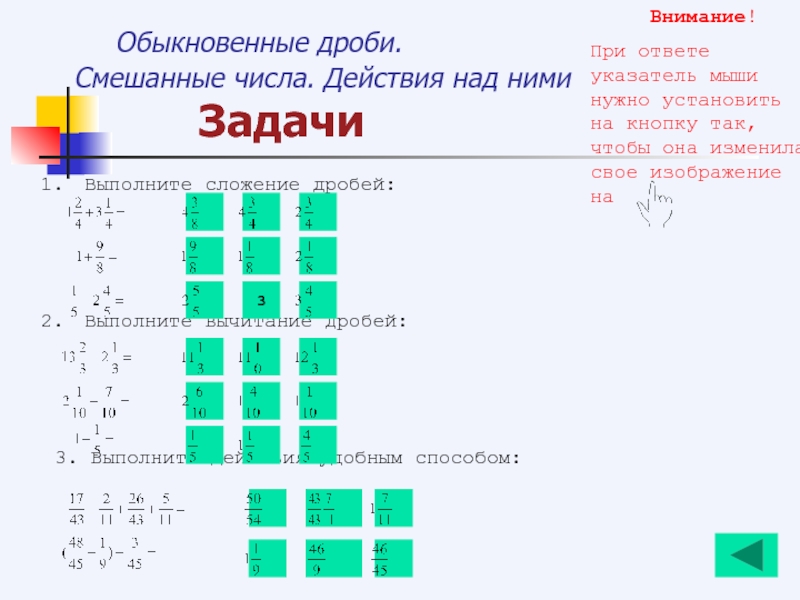
Слайд 92
Выполните сложение дробей:
Выполните вычитание дробей:
3. Решите уравнение:
Обыкновенные дроби.
н
н
1
Внимание!
При ответе указатель мыши нужно установить на кнопку так, чтобы она изменила свое изображение на
Слайд 93Разделим 5 яблок между 4 детьми. Можно это сделать так –
тогда каждый ребенок получит
по 5 частей, т.е .
Поступим по другому: дадим каждому по целому яблоку и оставшееся яблоко разделить на 4 части.
Тогда каждый получит яблока.
Сумму принято записывать короче .
Запись читают так: «Одна целая и одна четвертая».
Такое число называется смешанной дробью,
в которой 1 называют целой частью, а - его дробной частью.
И в первом и во втором случае мы смогли поровну разделить яблоки между детьми. Таким образом получается,
что числа и равны: .
Обыкновенные дроби.
Смешанные числа. Действия над ними
Слайд 94Обыкновенные дроби. Смешанные числа. Действия над ними
Число, которое будет характеризовать данную
где 2 – целая часть числа, - дробная часть числа. По другому это же число можно получить делением 11 на 4, т.е.
Чтобы из неправильной дроби выделить целую часть, надо:
Разделить числитель на знаменатель с остатком;
Неполное частное будет целой частью
Остаток дает числитель, а делитель – знаменатель дробной части.
Например: Запишем неправильную дробь в виде смешанного числа.
Делим 47 на 9. Неполное частное равно 5, а остаток равен 2.
Значит, .
Чтобы представить смешанное число в виде неправильной дроби, надо:
1. Умножить его целую часто на знаменатель дробной части;
2. К полученному произведению прибавить числитель дробной части;
3. Записать полученную сумму числителем, а знаменатель дробной части оставить без изменения.
Например: Запишем смешанное число в виде неправильной дроби.
Делим 5 умножим на 9, получим 45. полученному произведению прибавим 2 – 47. Получим дробь .
Слайд 95Обыкновенные дроби. Смешанные числа. Действия над ними
Рассмотрим как нужно поступать если
Напомним, что операция сложения подчиняется переместительному закону сложения.
И так на тарелке яблок. Сколько будет лежать яблок, если на нее положит еще ?
Так как смешанные числа представляют собой сумму целой и дробной части, то мы можем отдельно сложить целые и дробные части:
+
=
Если в процессе сложения дробная часть будет собой представлять неправильную дробь, то необходимо выделить целую часть и добавить ее к имеющейся.
Слайд 96При вычитании смешанных чисел нужно поступить согласно закону вычитания.
Так как смешанные
И так, на тарелке яблок. Сколько будет лежать яблок, если с нее забрать ?
-
=
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробная часть вычитаемого, то необходимо из целой части уменьшаемого выделяют одну единицу.
или короче:
Аналогично вычитают смешанные числа из натуральных.
Обыкновенные дроби. Смешанные числа. Действия над ними
Слайд 97Выполните сложение дробей:
Выполните вычитание дробей:
3. Выполните действия удобным способом:
Внимание!
При ответе указатель мыши нужно установить на кнопку так, чтобы она изменила свое изображение на
3
Слайд 98 Десятичные
дроби
Понятие
Сравнение десятичных дробей
Сложение и вычитание десятичных
Приближенное значение. Округление чисел
Умножение десятичных дробей
Проценты
Деление десятичных дробей
выход
Слайд 99Десятичные дроби
Понятие.
Например: 1 метр содержит 100 сантиметров,
10 дециметров; 1 килограмм
Тогда, наоборот 1 сантиметр составляет метра, дециметра,
1 грамм составляет килограмма,
1 копейка составляет гривны и т.д.
Знаменатели этих дробей числа 10, 100, 1000
и т.д.
Все единицы мер, которые используются в жизни соотносятся между собой десятыми, сотыми, тысячными долями.
Слайд 100Такие дроби у которых знаменателем являются числа 10, 100, 1000 принято
целую часть отделяют от дробной части запятой.
Например: вместо пишут 6,3 (читают: «6 целых 3 десятых»).
Так 6 дм 3 см= дм=6,3дм; 4 гр. 17 коп= р.=4,17 гр.
Если десятичная дробь правильная (ее целая часть отсутствует , то перед запятой пишут 0: =0,57(читают: «ноль целых 57 сотых).
Числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе. Тогда, если цифр меньше, то их приписывают слева.
Например:
десятичные дроби. Понятие.
Слайд 101Какая десятичная дробь соответствует обыкновенной:
Какая десятичная дробь соответствует частному:
47:10= 9:10=
6827:100= 33:100=
123:10= 15:1000=
3. Какая обыкновенная
0,2= 0,5=
0,25= 1,05=
4. Какую десятичную дробь можно представить в виде суммы разрядных слагаемых:
Десятичные дроби.
Понятие.
Задачи.
0,02
0,20
0,5
0,005
0,05
0,50
5,417
541,7
0,417
41,7
1,02
0,12
0,2
0,05
0,5
1,2
4,17
54,17
0,47
0,047
4,7
0,123
0,6827
68,27
1,23
6,827
12,3
0,09
90
0,9
1,5
0,033
0,33
0,15
3,3
0,015
80,808
808,08
88,8
Слайд 102Если взять отрезок АВ, длиной 6см=60мм и сравнить его длину в
6см = 0,6дм, 60мм = дм = 0,60дм.
Таким образом, десятичные числа 0,6 и 0,60 выражают длину одного и того же отрезка, эти дроби равны: 0,6=0,60.
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной.
Например:
0,87=0,870; 0,5400=0,54; 21=21,0=21,00.
Десятичные дроби
Сравнение десятичных дробей.
Слайд 103Сравним две десятичные дроби: 3,596 и 3,57.
Десятичные дроби сравнивают по
Сравнивать надо начиная со старших разрядов 3=3; 0,5=0,5; 0,09>0,07 – тогда 3,596 > 3,57
Проверим сравнение чисел с помощью сравнения обыкновенных дробей. Уравняем число знаков после запятой: 3,596 и 3,570. Сравним эти дроби, представив их в виде неправильных: и .У этих дробей одинаковые знаменатели, значит из них больше та, у которой числитель больше: 3596>3570 тогда и 3,596>3,57
Чтобы сравнить две десятичные дроби, можно сначала уравнять у них число десятичных знаков, а потом отбросив запятую, сравнить получившиеся натуральные числа
или сравнивать по разрядам начиная со старшего.
На координатном луче равные дроби будут определять одну и ту же точку, большая дробь располагается правее меньшей.
Сравним на координатном луче числа: 0,4 , 0,6 , 0,60 и 0,8 ,разделив единичный отрезок на 10 частей, каждую из которых еще на 10. Таким образом:0,4 < 0,6 < 0,8.
десятичные дроби. Сравнение десятичных дробей.
А
В
С
Д
Слайд 104Сравните десятичные дроби:
0,3 и 0,4 0,6 и 0,59
0,59 и 0,587 0,79 и 0,8
17,99
2. Какую цифру можно поставить вместо звездочки, чтобы неравенство было верным:
2,*1 < 2,02 6,413 > 6,4*8
0,3982 < 0,3*84 1,892 < 1,*0765
4,5*8 > 4,493 5*,683 < 50,6*1
3. Сравните числа, не восстанавливая цифры:
4,3** и 4,7** **,412 и *,9*
95,0** и 94,*3* *,*** и **,**
4. Какие натуральные числа стоят между числами
3,7 и 5,03 18,2 и 18,9
4,7 и 6,6 43,5 и 45,42
Десятичные дроби.
Сравнение.
Задачи.
=
<
>
=
<
<
=
>
>
>
<
=
=
<
>
=
<
>
0
1
2
8
9
0
7
1
0
любую
8
любую
9
9
0
=
>
>
<
<
<
=
>
<
=
>
<
3;4;5
4;5
3,9;4
5;6
4;5;6
Нет
нет
18,5
18;19
нет
44,5
44;45
0
1
любую
Слайд 105Десятичные дроби
Сложение и вычитание десятичных дробей.
Чтобы прибавить десятичные дроби 3,7
Проверим сложение, сложив эти дроби в виде обыкновенных:
Значит,
Мы получили один и тот же результат.
Слайд 106десятичные дроби. Сложение и вычитание десятичных дробей.
Найдем разность тех же чисел
Проверим вычитание, найдя разность этих дробей в виде обыкновенных:
Мы получили один и тот же результат.
Алгоритм сложения (вычитания) десятичных дробей:
Уравнять в этих дробях количество знаков после запятой;
Записать их друг под другом так, чтобы запятая была под запятой;
Выполнить сложение (вычитание), не обращая внимание на запятую;
Поставить в ответе запятую под запятой
Слайд 107десятичные дроби. Сложение и вычитание десятичных дробей.
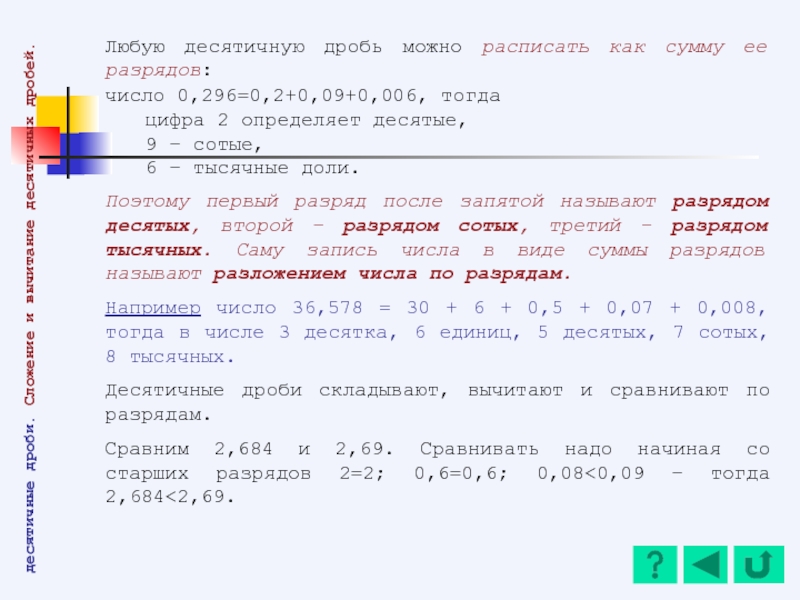
Любую десятичную дробь можно расписать
число 0,296=0,2+0,09+0,006, тогда
цифра 2 определяет десятые,
9 – сотые,
6 – тысячные доли.
Поэтому первый разряд после запятой называют разрядом десятых, второй – разрядом сотых, третий – разрядом тысячных. Саму запись числа в виде суммы разрядов называют разложением числа по разрядам.
Например число 36,578 = 30 + 6 + 0,5 + 0,07 + 0,008, тогда в числе 3 десятка, 6 единиц, 5 десятых, 7 сотых, 8 тысячных.
Десятичные дроби складывают, вычитают и сравнивают по разрядам.
Сравним 2,684 и 2,69. Сравнивать надо начиная со старших разрядов 2=2; 0,6=0,6; 0,08<0,09 – тогда 2,684<2,69.
Слайд 108Десятичные дроби.
Сложение и вычитание.
Задачи.
Вычислите:
3,7+1,1= 2,87-0,64=
7,53+2,46= 10-0,25=
7,55+2,46= 68,3-23,8=
2. Вычислите удобным способом:
0,27+1,78+5,73=
1,777+9,878+2,223=
37,45-(26,45+8,88)=
23,63+9,78-2,63=
6,73-(4,73-2,87)=
3.Решите уравнения:
х+7,54=8,24
3,99-х=0,88
х-16,53=14,47
3,81
4,8
3,711
7,776
7,532
9,101
9,11
2,56
2,814
10,75
9,25
65,92
45,5
6,78
7,73
5,7
5,8
14,223
8
6,87
0,87
19,88
14,78
23,63
33,78
15,78
0,78
4,87
4,11
2,06
21,06
9,99
10,01
2,23
9,75
44,5
7,78
1,14
13,878
2,12
30,78
4,87
0,7
3,11
31
Слайд 109Десятичные дроби
Приближенное значение чисел. Округление.
На рисунке видно, что арбуз
Длина отрезка АВ больше, чем 4см и меньше, чем 5см. Если обозначить х - длину отрезка, то 4 Если a
Слайд 110Длина отрезка АВ ближе к 5см, чем к 4см. Говорят, что
Если отрезок измерить более точно, то заметим, что его длина больше, чем 4,5 , но меньше чем 4,6 и ближе находится к числу 4,6 мы округлили число до десятых. Говорят: «Длина отрезка АВ приблизительно равна 4,6». Обозначают знаком ≈.
Алгоритм округления.
1. Определить разряд, до которого необходимо округлить число;
2. Если после разряда стоит цифра 0,1,2,3,4, то цифра этого разряда остается без изменения, младшие заменяются нулями, если они целые и отбрасываются , если они дробные: десятые, сотые, тысячные;
3.Если после разряда стоит цифра 5,6,7,8,9, то цифра этого разряда увеличивается на 1, младшие заменяются 0, если они целые и отбрасываются , если они дробные: десятые, сотые, тысячные;
Например:
необходимо округлить число 53,846 до целых. Получим 54.
необходимо округлить число 53,846 до десяток. Получим 50.
необходимо округлить число 53,846 до десятых. Получим 53,8.
необходимо округлить число 53,846 до сотых. Получим 53,85.
Слайд 111Десятичные дроби.
Приближенное значение. Округление.
Задачи.
Округлите 0,909:
до единиц
до десятых
до сотых
2.
до десяток до десятых
до единиц до сотых
3. Найдите приближенное значение числа 1,25
с недостатком
c избытком
4. Какое из чисел соответствует неравенству: 4
5. Решите уравнение 25x-9x=12 и результат округлите
до десяток до десятых
до единиц
0,9
0
0,91
1
1
0,90
81
8
82
80
80
81,1
81,00
81
1
1,2
1,25
1,3
6
6,1
3,9
4
1
10
10
0
0,7
0,75
1
0,9
0,91
80
81
81,01
81
1,2
1,3
5
4,8
5,99
0,8
0
1
Слайд 112Десятичные дроби
Умножение десятичных чисел
Умножим десятичное число 1,83 на 4 в
результате запятой отделим столько цифр справа,
сколько их в десятичном числе (два знака).
Проверим наши действия.
Умножить любое число на натуральное, это равносильно сложению.
Так: 1,83*4=1,83+1,83+1,83+1,83=7,32.
Мы получили тот же результат.
Алгоритм умножения десятичного числа на натуральное:
Умножить числа, не обращая внимания на запятую;
В полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Слайд 113Умножим десятичное число 1,83 на 10.
На справа нули можно не
тогда 1,83*10=18,3
Умножим десятичное число 1,83 на 100. Аналогично 1,83*100=183.
Заметим, что при умножении десятичной дроби на 10, 100, 1000 и т.д. число остается без изменения, но переносится запятая вправо на столько цифр, сколько нулей стоит в множителе.
Например: 0,0063*10=0,063 Мы перенесли запятую
на 1 знак вправо.
0,0063*100=0,63 Мы перенесли запятую
на 2 знака вправо.
0,0063*1000=6,3 Мы перенесли запятую
на 3 знака вправо
Чтобы умножить десятичное число на 10, 100, 1000 и т.д., надо в этом числе перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Слайд 114Алгоритм умножения десятичного числа на десятичное:
Умножить числа, не обращая внимания на
В полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в обоих множителях вместе.
Например: 0,254*0,03=0,00762.
В произведении получилось цифр меньше, чем надо отделить запятой, тогда нули дописывают.
Умножить число на 0,1; 0,01; 0,001 и т.д. – то же самое, что разделить число на 10, 100, 1000.
Поэтому воспользуемся правилом:
Чтобы умножить десятичное число на 0,1; 0,01; 0,001 и т.д., надо в этом числе перенести запятую на столько цифр влево, сколько нулей стоит в множителе перед единицей.
Например: 6,3*0,1=0,63 Мы перенесли запятую
на 1 знак влево.
6,3*0,01=0,063 Мы перенесли запятую
на 2 знака влево.
Слайд 115Десятичные дроби.
Умножение.
Задачи.
Выполните умножение:
4*0,2= 5*0,2=
8*0,05= 7*0,04=
2. Выполните умножение на разрядную
13,5*10= 10,01*10=
1,3*100= 1,3*1000=
3. Выполните умножение на десятичные разряды:
9*0,001= 0,13*0,1=
100*0,001= 1,32*0,01=
4. Выполните умножение:
1,9*0,6= 0,6*0,03=
1,3*1,1= 0,12*0,4=
0,42= 0,13=
5. Выполните умножение удобным способом:
(19,3*5)*20= 2,5*1,47*4=
0,2*3,87*0,5= (1,25*4)*0,8=
0,08
8
0,04
4
32
3,2
0,01
0,1
1001
10,1
13
1300
1
10
0,48
4,8
19,3
193
40
0,4
1350
1,35
0,9
0,09
1,32
0,132
0,018
1,8
0,016
1,6
11,4
114
130
13
1,3
0,13
143
14,3
0,01
0,0001
147
1,47
3,87
38,7
0,8
0,4
1
0,32
100,1
1300
135
130
0,009
0,1
0,013
0,0132
0,18
0,048
0,001
1,43
0,16
1,14
1930
0,387
4
14,7
Слайд 116Десятичные дроби
Деление десятичных чисел на натуральные числа.
Разделим десятичную дробь
Если целая часть меньше делителя,
то в частном целая часть равна нулю.
Проверим деление умножением частного на делитель:
Мы получили верный результат.
Слайд 117
Чтобы разделить десятичное число на 10, 100, 1000 и т.д., надо
Обыкновенную дробь можно перевести в десятичную делением числителя на знаменатель:
Проверьте и запомните некоторые
значения обыкновенных дробей.
Слайд 118Чтобы разделить десятичную дробь на десятичную нужно:
В делимом и делителе перенести
Выполнить деление десятичного числа на натуральное.
Например: разделим 2,88 на 0,8.
Для этого перенесем запятую вправо в числах на 1 цифру: 2,88:0,8=28,8:8.
Теперь разделим в столбик
и получим 2,88:0,8=3,6
Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д. это все равно, что умножить на 10, 100, 1000. Таким образом запомните правило:
Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей.
Например: 0,0063:0,1=0,063 Мы перенесли запятую
на 1 знак вправо.
0,0063:0,01=0,63 Мы перенесли запятую
на 2 знака
вправо.
Слайд 119Десятичные дроби.
Деление.
Задачи.
Выполните деление:
1,8:6= 6,9:3=
4,8:2= 1,44:12=
2. Выполните деление на разрядную единицу:
6:100= 10,01:10=
3. Выполните деление на десятичные разряды:
9:0,001= 0,13:0,1=
100:0,01= 1,32:0,01=
4. Выполните деление :
1,8:0,6= 0,6:0,03=
1,4:0,4= 0,12:0,6=
5. Вычислите удобным способом:
(7,7*6):7= (8,8*9):11=
(17:25):4= (6,4*5,8):64=
0,03
3
2,04
0,24
0,23
23
1,3
0,13
0,6
6
0,1001
100,1
13,2
0,0132
1000
0,001
0,3
30
0,35
35
0,2
2
58
5,8
0,72
72
0,66
66
1,7
17
1,2
0,012
1300
0,13
0,009
90
13
0,013
нет
нет
2
20
2,4
0,3
2,3
0,12
1,001
0,0013
0,013
0,06
9000
10000
1,3
132
20
0,2
3
3,5
6,6
0,17
7,2
0,58
Слайд 120Десятичные дроби
Проценты.
Так как мы все вычисления производим в десятичной системе
Так: 1 сантиметр – это сотая часть метра,
1 копейка – сотая часть гривны,
сотую часть гектара принято называть аром или соткой.
Введено понятие – процент.
Процентом называют одну сотую часть. Обозначают знаком %.
Говорят: «В классе 75% учеников написали контрольную работу по математике на достаточный и высокий уровень»,
« Банк ежегодно выплачивает 12% от вложенной суммы».
Если 1% равен сотой части числа,
то все число составляет 100%.
Слайд 121Рассматривают три типа задач.
1.Известно число, необходимо определить часть
Например:
В магазин завезли 320кг
конфет, из которых 75% -
шоколадных.
Сколько килограмм составляют
шоколадные конфеты?
Решение:
Так как 320 кг конфет – это 100%, то, чтобы найти 1% нужно 320 разделить на 100, получим 3,2 кг. Чтобы найти, чему равны 75% конфет нужно умножить 3,2 на 75. 75*3,2=240.
Так, 240 кг составляют шоколадные конфеты.
В результате рассуждений мы заданное число (320) умножили на проценты (75) и результат разделили на 100.
(320:100*75=240.)
Известно: число и процент части
Найти: часть.
Алгоритм решения:
число разделить на 100
Результат умножить на процент
Слайд 1222. Известна часть числа и ее процент, необходимо определить само число.
Например:
За контрольную по
математике 12 учеников
получили оценку
«высокого уровня»,
что составляет 30%.
Сколько учеников в классе?
Решение:
Узнаем чему равен 1%. Для этого 12 разделим на 30. 12:30=0,4. Значит 1% равен 0,4. Все ученики класса составляют 100%. Умножим 0,4*100=40. В классе 40 учеников.
В результате рассуждений мы часть числа (12) разделили на его проценты (30) и результат умножили на 100. (12:30*100=40.)
Известно: часть числа и ее процент.
Найти: само число.
Алгоритм решения:
Часть числа разделить на его процент
Результат умножить на 100
Слайд 1233. Известно число и часть числа. Необходимо узнать какой процент составляет
Например:
Вся площадь поля составляет
1800га, картофелем засажено
558га.
Какой процент поля засажен?
Решение:
Определим какую часть от общего поля составляет засаженная площадь картофеля, для этого 558 разделим на 1800. 558:1800=0,31. Значит, картофелем засажена 31 сотая часть поля, т.е. 1%. Умножим 0,31 на 100%. 0,31*100=31%.
В результате рассуждений мы часть числа (558) разделили на все число (1800) и результат умножили на 100. (558:1800*100=31.)
Известно: число и его часть.
Найти: какой процент составляет часть от числа.
Алгоритм решения:
Часть числа разделить на само число
Результат умножить на 100
Слайд 124Десятичные дроби.
Проценты
Задачи.
Выразите проценты в виде десятичного числа:
1%= 75%=
20%= 100%=
50%= 120%=
2. Выразите
0,02= 1,25=
0,5= 4,6=
0,17= 6,006=
3. Найдите 1% от:
20 156
140 68,25
100
0,1
0,02
2
0,1
10
0,12
0,012
500
5
20
200
1,25
12,5
0,6006
60,06
2
20
14
0,14
156
15,6
0,05
5
7,5
750
1,7
0,17
0,46
46
6825
6,825
0,01
0,2
0,5
0,75
1
1,2
125
460
600,6
50
17
2
0,2
1,4
1,56
0,6825
Слайд 125Десятичные дроби.
Нахождение части числа по его проценту.
Задачи.
1. Найдите
2% от числа
15% от числа 500 0,5% от числа 15
2. Масса Земли 5975 квинтиллионов тонн. Масса воды составляет 9%. Какова масса воды земли?
3. Яблоки при сушке теряют 84% своей массы. Сколько получится сушеных яблок из 300 кг свежих?
4. В классе 30 учеников, из них 20% учатся в музыкальной школе, 50% посещают спортивные секции, а остальные посещают кружки иностранных языков. Сколько учащихся посещают кружки иностранных языков?
0,42
42
7,5
0,75
7,5
0,75
5377,5 кв.т
53,775 кв.т
480
18,75
6
10
н
н
0,5
5
50
0,075
75
4,2
537,75 кв.т
48
9
Слайд 126Десятичные дроби.
Нахождение числа по его части и ее проценту
Задачи.
Найдите число, если:
5%
10% его равны 90 125% его равны 250
2. Из зеленого чайного листа получают 4% чая. Сколько надо чайного листа, чтобы получить 5,6 кг чая?
3. Ромашка при сушке теряет 84% свей массы. Сколько надо взять свежей ромашки чтобы получилось 32 кг сухой?
4. Ученик в первый день прочитал 15% всей книги, что составляет 60 станиц, во второй день он прочитал 200 страниц. Сколько ему осталось прочитать?
1,5
60
9
90
3,5
50
14
0,224
5,12
38,09
10
30
312,5
20
900
600
200
500
140
200
200
Слайд 127Десятичные дроби.
Нахождение процента по числу и части.
Задачи.
Сколько процентов составляет:
28 от 40 63
102 от 425 500 от 250
2. Если в стакан чая (200г) положить 2 чайные ложки сахара (по 10г), то какова будет концентрация сахара в чае?
3. Поверхность Земли 510,1 млн км2. Суша занимает 149,2 млн км2, остальная поверхность покрыта водой. Сколько процентов поверхности Земли покрыто водой?
4. Стоимость товара понизилась от 400 грн до 360 грн. На сколько процентов снизилась стоимость товара?
7%
700%
240%
2,4%
50%
5%
1%
0,1%
20%
7%
111%
90%
8,4%
840%
70%
24%
84%
200%
10%
70%
10%
Слайд 128 Основы геометрии
Точка. Отрезок.
Плоскость. Прямая. Луч.
Многоугольники.
Периметр и площадь
Угол. Измерение углов.
Окружность и круг.
Прямоугольный параллелепипед.
Понятие объема.
выход
Слайд 129Основы геометрии
Точка. Отрезок.
Возьмем в руки простой карандаш и поставим точку,
Если к точкам А и В приложить линейку и соединить их линией, то получится отрезок АВ или ВА. Точки А и В называют концами отрезка АВ.
Существуют точки принадлежащие (E, K) и не принадлежащие (O, M) заданному отрезку АВ.
Любые две точки можно соединить одним и только одним отрезком.
Слайд 130Возьмем отрезок длиной 1см. Если отложить такой отрезок АВ, что его
Отрезки можно сравнивать
с помощью циркуля
и измерять с помощью линейки.
Так, отрезок АВ
длиннее отрезка CD
и короче отрезка EM.
Слайд 131В треугольнике отрезки AB, BC, CA называются сторонами треугольника, а точки
Чтобы назвать многоугольник перечисляют по порядку все его вершины.
Например говорят: «треугольник ABC»,
«пятиугольник OTLPN».
Возьмем несколько отрезков
разной длины и соединим их,
получим ломанную линию.
Если концы ломанной линии соединить, то получиться многоугольник. Так образуются треугольники, четырехугольники, пятиугольники и т.д.
Слайд 132Сколько отрезков изображено на рисунке?
Сколько отрезков изображено на рисунке?
Какие точки
Точка К принадлежит отрезку АВ. АК=5см, АВ=16см, чему равна длина отрезка КВ?
Точка. Отрезок.
Задачи.
8
6
7
10
7
10
6
E
K
8
C
A
L
D
21
12
11
Слайд 133Основы геометрии
Плоскость. Прямая. Луч.
Посмотрите на поверхность стола или доски, оконного
На плоскости можно расположить точку, несколько точек. Любые две точки можно соединить отрезком.
Все построения, которые мы будем выполнять в тетради или на доске, мы выполняем на плоскости.
Слайд 134Начертим отрезок АВ и продолжим его по линейке в обе стороны.
Через любые две точки проходит единственная прямая. Прямая не имеет концов, она неограниченно продолжается в обе стороны.
На плоскости есть точки, которые принадлежат прямой (А и В) и точки не принадлежащие прямой (С).
Две прямые могут пересекаться, тогда они имеют одну общую точку.
Если прямые имеют две общие точки, то они совпадают.
Если прямые не пересекаются и не совпадают, т.е не имеют общих точек, то они параллельны.
(противоположные края стола параллельны, углы стен параллельны).
Слайд 135
На прямой АВ возьмем точку О. Она делит прямую АВ на
Это и называют лучом. Говорят: «луч ОА», «луч ОВ».
Точка С принадлежит лучу ОА, точка Д не принадлежит лучу ОА.
Лучи, образованные точкой на одной прямой называют дополнительными друг другу.
Например: Луч ОА является дополнительным лучу ОВ и наоборот.
С
Слайд 136Сколько лучей изображено на рисунке?
2. Какие лучи пересекаются?
3. Какие прямые параллельны?
4.
5. Определите, на сколько частей прямые разбивают плоскость.
Плоскость. Прямая. Луч.
Задачи.
В
K
L
6
4
2
3
BE и FK
AD и CN
BE и AD
CN и FK
BE и CN
AD и FK
AB и KL
CD и KL
AB и CD
N
M
A
C
L
10
6
9
Слайд 137Есть точки, которые лежат внутри угла АОВ (С), точки, которые лежат
Тогда, лучи, образующие угол, называются сторонами угла, а общая точка – вершиной угла.
Углы называют по названию лучей, с вершиной внутри.
Так, на рисунке изображен угол АОВ, со сторонами ОА и ОВ, вершиной О. Для обозначения используют специальный знак .
Так, ОАВ, или О.
Основы геометрии
Угол. Измерение угла.
Два луча, выходящие из одной точки разбивают плоскость на две полуплоскости.
Сами лучи и одна из этих полуплоскостей образуют фигуру, которую называют углом.
Слайд 138Наложим углы так, чтобы вершины совпали
и одни стороны совпали, то
который будет находиться внутри другого
назовем меньшим.
В нашем примере АОВ и CKF расположили так, что вершины О и К совпали и стороны ОВ и FK совпали. Видно, что CFK лежит внутри АОВ, тогда CFK < AOB
Углы можно сравнивать методом наложения.
Если при наложении углов вершины и стороны углов совпадут, то углы называют равными.
Пишут: АОВ= CKF
Слайд 139
Возьмем лист бумаги и согнем его пополам.
Угол, образованный стороной листа
Такой угол можно получить дополнительными лучами.
Угол АОВ – развернутый.
Два дополнительных луча образуют развернутый угол.
Сложим лист еще пополам. Образовался угол. Если развернуть лист бумаги, то видим, что таких угла образовалось 4. Каждый из них равен половине развернутого. Такие углы называются прямыми.
Прямым углом называется угол, равный половине развернутого.
Чтобы изобразить
прямой угол используют
чертежный треугольник.
Угол АОВ – прямой.
В жизни мы часто видим и используем прямые углы:
углы стола, углы стен и т.д.
Слайд 140Для измерения углов применяют транспортир. Шкала транспортира располагается по окружности. Центр
Полуокружность транспортира разделена на 180 равных частей. Принято считать, что градусная мера развернутого угла равна 180°.
Тогда градусом называют -ю долю развернутого угла.
Углы измеряются в градусах.
Чтобы измерить угол нужно совместить вершину угла с меткой центра полуокружности транспортира, а одну из сторон угла с нулевой отметкой (началом отсчета), на продолжении второй стороны угла нужно увидеть отметку, которая и определит размер угла.
Например: АОВ=50°, СОВ=120°
Слайд 141Равные углы имеют равную градусную меру, меньший угол имеет меньшую градусную
Транспортир применяют для построения углов заданной градусной меры.
Развернутый угол имеет градусную меру 180°.
Прямой угол равен 90°.
Углы меньше 90° называются острыми.
Например: АОВ=45° - острый.
Углы больше 90° называются тупыми.
Например: CKF=135° - тупой.
С
K
F
135°
Слайд 142Угол. Измерение угла.
Задачи.
1. Какие из углов тупые?
2. Какие из углов острые?
3.
4. Какой угол образуют часовая и минутная стрелки часов в 6ч?
5. Какой угол образуют часовая и минутная стрелки часов в 20ч?
6. Сколько углов изображено на рисунке?
7. Луч ОК делит развернутый угол АОВ на два угла так, что АОК=1200. Найдите ВОК.
AOK
AOB
AOC
BOC
BOK
COK
AOB
AOC
COK
BOK
BOC
AOK
1800
1200
900
900
450
1350
2400
1200
1800
6
3
4
600
3000
400
Слайд 143Основы геометрии.
Многоугольники. Периметр и площадь многоугольников.
Если концы ломанной линии соединить, то
В треугольнике отрезки AB, BC, CA называются сторонами треугольника, а точки A, B и С называются вершинами треугольника.
Чтобы назвать многоугольник перечисляют по порядку все его вершины.
Например говорят: «треугольник ABC»,
«пятиугольник OTLPN».
Слайд 144Геометрия изучает несколько основных фигур.
Более сложные фигуры можно получить из
К основным фигурам относятся: треугольники,
несколько видов четырехугольников, круг и
его части.
Например возьмем отрезки длиной 5см, 3см, 7см. Из данных отрезков построим треугольник АВС.
Возьмите отрезки 5см, 1см и 2 см. Попробуйте построить треугольник. Треугольник не получиться.
И так, не всякие отрезки определяют треугольник.
Фигура, полученная соединением нескольких отрезков называют многоугольником. К многоугольникам относятся: треугольники, четырехугольники, пятиугольники и т.д.
Рассмотрим многоугольник, образованный тремя отрезками.
5см
1см
2см
Слайд 145Если соединить четыре отрезка, то получим четырехугольник.
К основным четырехугольникам
относятся:
Рассматривают частные случаи параллелограмма – это прямоугольники, квадраты, ромбы.
Сумму длин сторон многоугольника называют его периметром. Периметр обозначают латинской буквой Р
Например: найдите периметр треугольника со сторонами 5см, 7см, 3см.
Решение: Р=5см+7см+3см=15см
Найдите периметр прямоугольника со сторонами 2см и 5см (у прямоугольника стороны попарно равны)
Решение: Р=2см+5см+2см+5см=2*(2см+5см)=14см
Найдите периметр квадрата со стороной 5см. (у квадрата все стороны равны)
Решение:
Р=5см+5см+5см+5см=4*5см=20см
A
A
B
B
C
C
D
D
Слайд 146За единицу измерения площади фигуры принята площадь одного квадрата со стороной
Пишут: 1см2 и говорят: «один квадратный сантиметр».
Многоугольник можно разбить на несколько квадратов со стороной 1см2 . Если фигуру разбили на р квадратов, то ее площадь равна р см2
Площадь обозначают буквой S.
Для основных фигур выведены формулы.
Для нахождения площади прямоугольника: S=а*в
Для квадрата: S=а*а=а2
Для треугольника: S= а*h, где h – высота треугольника, опущенная к стороне а.
Слайд 147 1. Найдите площадь квадрата со стороной 5см.
Решение: S=52=25см2
2. Найдите площадь прямоугольника
Решение: S=5*3=15см2
3. Найдите площадь треугольника со
стороной 7см и высотой 5см.
Решение: S= *5*7=17,5см2
4. Найдите площадь произвольного
многоугольника
Решение:
Способ1. Можно воспользоваться палеткой,
разделенной на квадраты со стороной 1см2
и подсчитать их количество: S≈8,3см2
Способ2. Можно разбить фигуру на основные,
найти их площади и сложить. В данном случае
фигура состоит из квадрата и прямоугольника
S=4*1,5+1,5*1,5=6+2,25=8,25см2
Площадь любой фигура равна сумме
ее составляющих.
C
Слайд 148Чему равен периметр многоугольника?
Какая из данных фигур имеет площадь 24см2?
Найти периметр
АВ=2дм3см, ВС=15см, СА=17см.
4. Может ли существовать треугольник
со сторонами: 3см, 5см и 1см?
5. Площадь прямоугольника составляет 40см2,
одна из его сторон равна 5см.
Найти периметр прямоугольника.
6. Сколько треугольников на рисунке?
Многоугольники. Периметр и площадь многоугольников
Задачи.
14
16
15
19
5дм 5см
2дм 35см
4дм 5см
да
нет
26
13
40
8
6
2
Слайд 149Если соединить две любые точки окружности получится отрезок, который называют хордой.
Хорда отделяет от окружности две дуги.
Основы геометрии.
Окружность и круг.
Установим ножку циркуля с иглой в точку О, а с карандашом будем вращать вокруг этой точки. Тогда карандаш опишет замкнутую линию, которую называют окружностью.
Окружность делит плоскость на две части. Та часть плоскости, которая находится внутри окружности называется кругом.
Точку О называют центром окружности.
Все точки окружности находятся на одинаковом расстоянии от центра, которое называется радиусом.
О
А
В
С
Д
Слайд 150Основы геометрии.
Прямоугольный параллелепипед. Понятие объема.
В жизни мы часто имеем дело с
Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников, которые называются гранями. Противоположные грани прямоугольного параллелепипеда равны.
Стороны граней называют ребрами параллелепипеда, а вершины граней – вершинами параллелепипеда.
У прямоугольного параллелепипеда 6 граней, 12 ребер и 8 вершин.
Прямоугольный параллелепипед измеряется тремя измерениями: шириной (a), длиной (b) и высотой (c).
Частный случай прямоугольного параллелепипеда – куб, у него все измерения равны.
a
b
c
a
a
a
Слайд 151Чтобы найти объем прямоугольного параллелепипеда, нужно выяснить сколько кубиков с единичной
Сколько кубиков в каждом слое? (4*3=12).
А сколько во всех слоях? (12*4=48)
Объем обозначают буквой V.
Формула объема прямоугольного параллелепипеда: V=а*в*с
У куба все ребра равны,
тогда объем куба равен: V=а3.
Чтобы сравнить объемы двух сосудов, нужно один из них наполнить водой, а затем перелить в другой. Если вода останется, то первый сосуд больше второго, если вся вода войдет во второй и полностью его заполнит, то объемы сосудов равны.
Единицей измерения объема принят 1л=1дм3, т.е. такой куб, у которого все стороны равны 1дм.
1 дм
1 дм
1 дм
a
Слайд 152Прямоугольный параллелепипед. Понятие объема.
Задачи.
1. Найдите площадь поверхности прямоугольного параллелепипеда.
3. Сколько сантиметров проволоки надо взять для изготовления каркаса этого параллелепипеда?
4. Объем куба равен 27см3. Чему равна площадь поверхности?
5. Какое решение соответствует 4-ой задачи, если сторону квадрата обозначить а?
512
480
416
608
608
512
480
768
32
64
608
128
128
64
36
54
а2=27, S=6*а3
а3=27, S=9*(2*а)
а3=27, S=6*а2
Слайд 153Исторические сведения
системы счисления
Человечеством было придумано много способов счета. Первым счетным инструментом
Так в Древней Руси обозначали числа буквами, над которыми ставили знак титло
Современная десятиричная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли ее у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы – «индийскими».
До сих пор используются и римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад (I-1, V-5, X-10, L-50, C-100, D-500, M-1000).
Кроме этих систем счисления существовали «пятиричные», «двенадцатиричные», «шестидесятиричные» и др.
Слайд 154В Древней Руси в качестве единиц измерения длины применялись: косая сажень
Слайд 155
Немецкого ученого Карла Гаусса называли королем математиков. Его математическое дарование проявилось
Слайд 156В наше время почти все народы пользуются счетом десятками, сотнями, тысячами,
Раньше некоторые народы применяли другие системы счета. В теплых странах Африки и Америки, где люди ходили босыми, для счета применялись не только пальцы рук, но и пальцы ног. Получался счет двадцатками. А пять тысяч лет назад в некоторых странах Востока пользовались шестидесятеричной системой счисления, т.е. системой счисления с основанием 60. Эта система была первой позиционной системой.
Следы шестидесятеричной системы счисления сохранились до сих пор: мы и сей час делим час на 60 минут, а минуту – на 60 секунд.
Использование числа 10 как основания системы счисления связано с тем, что у людей на руках 10 пальцев, которые удобнее всего было использовать при счете. Но основание системы счисления, конечно, может быть любым числом. Например, современные ЭВМ (электронно-вычислительные машины) считают в двоичной системе (основание 2), так как при этом используются только два состояния: «есть сигнал» и «нет сигнала».
Слайд 157Первые единицы длины как в России, так и в других странах
Для измерений больших расстояний на Руси использовали единицу «поприще», замененную позже верстой (в разных местностях версту считали по разному-от500 до 750 сажен).От восточных купцов пошла единица «аршин» (тоже означает «локоть»)-существовали турецкий аршин, персидский аршин и др. Поэтому и возникла поговорка «мерить на свой аршин».
Множество единиц существовало и для измерения массы. Наиболее древняя русская мера-«гривна», или «гривенка» (около 410 г), Позднее появились золотники, фунты, пуды.
В старину площади земельных участков измеряли в десятинах (это площадь квадрата со стороной, равной десятой части версты).
Во многих Западных странах использовалась единица площади акр. Акр примерно равен 4047 квадратных метров.
Слайд 158На Руси использовались в качестве измерения объема ведро (около 12 л),
Соотношения между мерами были сложны, существовали разные определения для единиц измерения. Это и затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введение единой системы мер, удобной для всех стран.
Такая система - ее назвали метрической системой мер - была разработана во Франции. Основную единицу длины 1 метр (от греческого слова «метрон»-мера) определили как сорокамиллионную долю окружности Земли, основную единицу массы 1 кг - как массу 1 кубический дм чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись10,100,1000 и т.д.