ДВФУ,
кандидат физико-математических наук
Луняков Юрий Вилорьевич,
т. 2679875 (+7 902 481 9875)
е-mail: luniakov@iacp.dvo.ru
Сайт с информационными материалами
для самостоятельного изучения:
ftp://ftp.dvo.ru/pub/Computers/
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учебный курс: Компьютерное моделирование полупроводников (5 курс) доцент кафедры физики низкоразмерных структур ИФИТ ДВФУ, кандидат физико-математических наук Луняков Юрий Вилорьевич, т. 2679875 (+7 902 481 9875) е-mail: luniakov@iacp.dvo.ru Сайт с и презентация
Содержание
- 1. Учебный курс: Компьютерное моделирование полупроводников (5 курс) доцент кафедры физики низкоразмерных структур ИФИТ ДВФУ, кандидат физико-математических наук Луняков Юрий Вилорьевич, т. 2679875 (+7 902 481 9875) е-mail: luniakov@iacp.dvo.ru Сайт с и
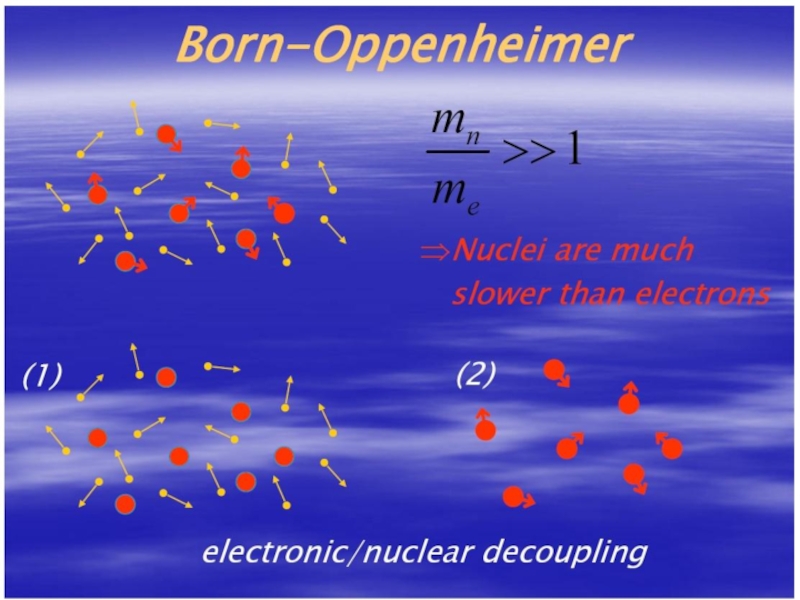
- 4. Электронное уравнение: где первый член в
- 13. Метод Хартри-Фока-Рутана Одноэлектронные волновые функции ϕi(r) ïðåäñòàâëÿþòñÿ
- 14. PRDDO, Partial Retention of Diatomic Differential Overlap)
- 15. Эмпирические методы где µ — фиктивная масса,
- 16. Эмпирические методы Потенциал взаимодействия между двумя молекулами
- 17. Некоторые двухчастичные потенциалы
- 18. Из физических соображений очевидно, что компоненты решёточной
Электронное уравнение: где первый член в сумме – кинетическая энергия электронов (Te), второй – потенциал взаимодействия между электронами и ядрами (Vne), а третий – потенциал взаимодействия между электронами (Vee). Потенциалом
Слайд 1Учебный курс: «Компьютерное моделирование полупроводников»
(5 курс)
доцент кафедры физики
низкоразмерных структур ИФИТ
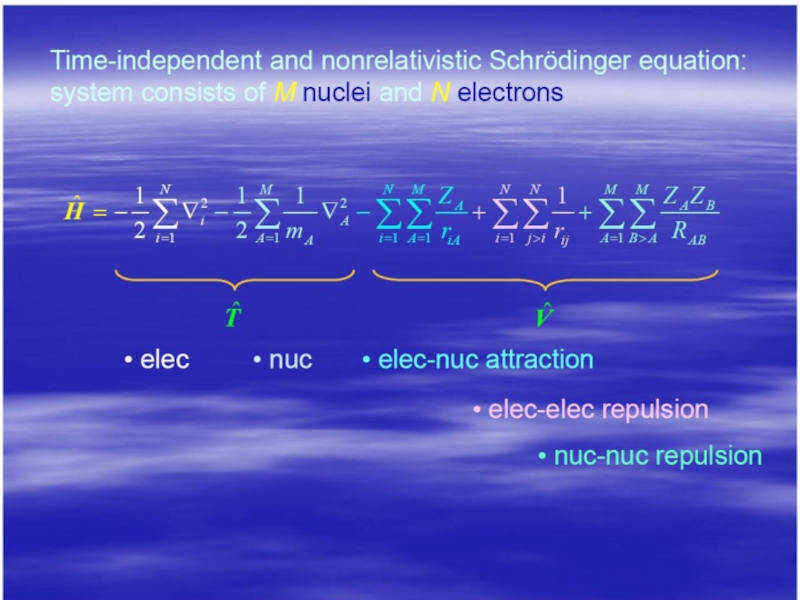
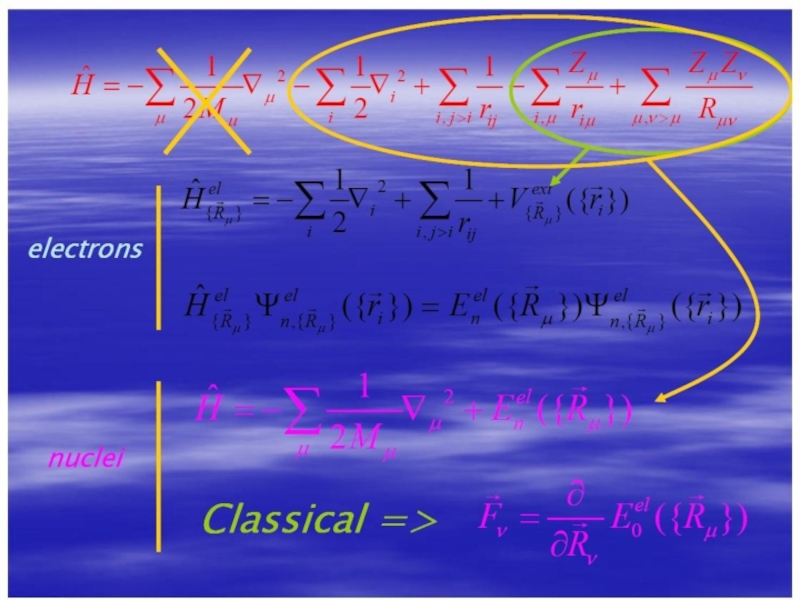
Слайд 4Электронное уравнение:
где первый член в сумме – кинетическая энергия электронов (Te),
второй – потенциал взаимодействия между электронами и ядрами (Vne), а третий – потенциал взаимодействия между электронами (Vee). Потенциалом взаимодействия между ядрами (Vnn) мы при дальнейшем рассмотрении пренебрегаем в силу того, что для каждой фиксированной конфигурации ядер это величина постоянная.
Если бы не было члена Vee, то гамильтониан сводился бы к:
Если бы не было члена Vee, то гамильтониан сводился бы к:
где h(i) – одноэлектронный оператор.
φ'i(i) – одноэлектронная функция (орбиталь), являющаяся решением одноэлектронного уравнения:
Поскольку электронный гамильтониан не зависит от спиновых операторов в используемом пока представлении, то орбиталь с учетом спина можно записать в виде φ'i(i)σ, где σ указывает на спин (1/2 или –1/2).
Слайд 13Метод Хартри-Фока-Рутана
Одноэлектронные волновые функции ϕi(r) ïðåäñòàâëÿþòñÿ â âèäå ðàçëîæåíèÿ ïî íåêîòîðîìó
áàçèñíîìó íàáîðó àòîìíûõ âîëíîâûõ ôóíêöèé ϕj(r):
При подстановке в уравнения Хартри-Фока получаем
По ходу вычисления матричных элементов приходится вычислять большое количество интегралов типа:
Слайд 14PRDDO, Partial Retention of Diatomic Differential Overlap) сохранение одно, двух и
трехцентровых кулоновских интегралов и двухцентровых обменных, N3 scaling.
Полуэмпирические методы
(ZDO, Zero Differential Overlap)
CNDO, Complete Neglect of Differential Overlap – для всех пар атомных орбиталей
INDO, Intermediate Neglect of Differential Overlap учитывает одноцентровые кулоновские < µµ|µµ > и обменные < µν|µν > интегралы и двухцентровые кулоновские интегралы < µµ|νν >.
MINDO, Modified Intermediate Neglect of Differential Overlap: MINDO/2 , MINDO/3
(MNDO, Modified Neglect of Diatomic Overlaps
(NDDO, Neglect of Diatomic Differential Overlap)
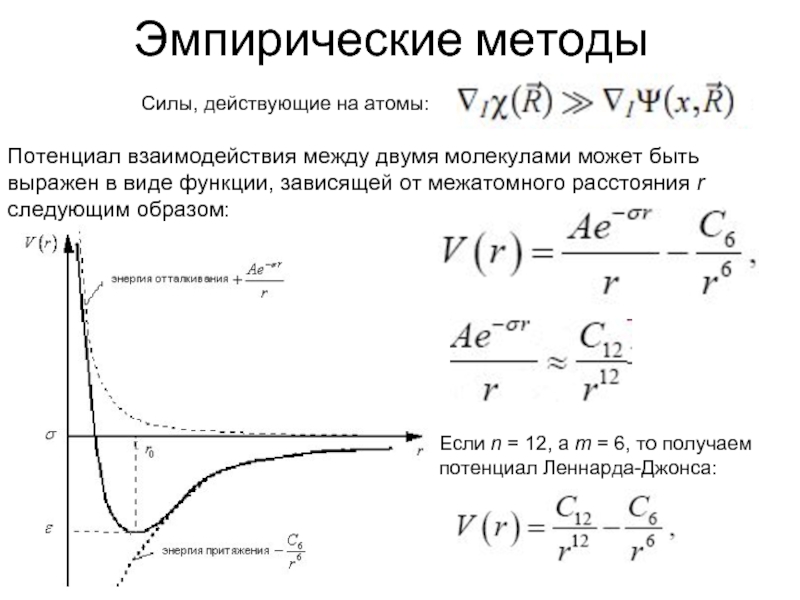
Слайд 15Эмпирические методы
где µ — фиктивная масса, ассоциированная с электронными волновыми функциями,
E — функционал энергии Кона-Шема, RI — позиция иона I, αn определяет размер и форму единичной ячейки.
Слайд 16Эмпирические методы
Потенциал взаимодействия между двумя молекулами может быть выражен в виде функции,
зависящей от межатомного расстояния r следующим образом:
Силы, действующие на атомы:
Если n = 12, а m = 6, то получаем потенциал Леннарда-Джонса:
Слайд 18Из физических соображений очевидно, что компоненты решёточной энергии можно разделить на
определяемые дальнодействующими (электростатическими) и короткодействующими (межатомными) потенциалами. Эти компоненты нуждаются в раздельном вычислении.
Для систем малых и средних размеров наиболее эффективный путь для расчета электростатической энергии — суммирование методом Эвальда. Результирующее выражение для энергии может быть представлено в виде двух быстросходящихся сумм в обратном и реальном пространствах:
Etotal = Erecip + Ereal
Erecip =
Для систем малых и средних размеров наиболее эффективный путь для расчета электростатической энергии — суммирование методом Эвальда. Результирующее выражение для энергии может быть представлено в виде двух быстросходящихся сумм в обратном и реальном пространствах:
Etotal = Erecip + Ereal
Erecip =
Ereal =
где G — вектор решётки в обратном пространстве, rij — межатомные расстояния, qi и qj — заряды на атомах, η — параметр, управляющий распределением сумм между прямым и обратным пространствами, erfc{} — дополнительная функция ошибок.
