Автор: ученика 8 класса Якунина Андрея
Руководитель: Бурукина Н.Н.
2011г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МОУ ООШ с.Никольское Духовницкого района Саратовской области Площадь прямоугольника и треугольника Автор: ученика 8 класса Якунина Андрея Руководитель: Бурукина Н.Н. 2011г. презентация
Содержание
- 1. МОУ ООШ с.Никольское Духовницкого района Саратовской области Площадь прямоугольника и треугольника Автор: ученика 8 класса Якунина Андрея Руководитель: Бурукина Н.Н. 2011г.
- 2. ПЛОЩАДЬ ТРЕУГОЛЬНИКА Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию
- 3. ОСНОВАНИЯ И ВЫСОТЫ ТРЕУГОЛЬНИКА
- 4. ПЛОЩАДЬ ТРЕУГОЛЬНИКА Теорема: площадь треугольника равна половине
- 5. СЛЕДСТВИЯ Площадь прямоугольного треугольника равна
- 6. СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И
- 7. ТЕОРЕМА: ЕСЛИ УГОЛ ОДНОГО ТРЕУГОЛЬНИКА РАВЕН
- 8. РАВНЫЕ МНОГОУГОЛЬНИКИ ИМЕЮТ РАВНЫЕ ПЛОЩАДИ
- 9. ПЛОЩАДЬ ВСЕГО МНОГОУГОЛЬНИКА РАВНА СУММЕ ПЛОЩАДЕЙ ЕГО ЧАСТЕЙ, НА КОТОРЫЕ ОН РАЗБИТ НЕКОТОРОЙ ПРЯМОЙ.
- 10. ПЛОЩАДЬ КВАДРАТА РАВНА КВАДРАТУ ДЛИНЫ ЕГО СТОРОНЫ,
- 12. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА: S=а·b
ПЛОЩАДЬ ТРЕУГОЛЬНИКА Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию
Слайд 1
МОУ «ООШ с.Никольское Духовницкого района Саратовской области»
Площадь прямоугольника и треугольника
Слайд 2ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Площадь треугольника равна половине произведения основания на высоту, проведённую к
этому основанию
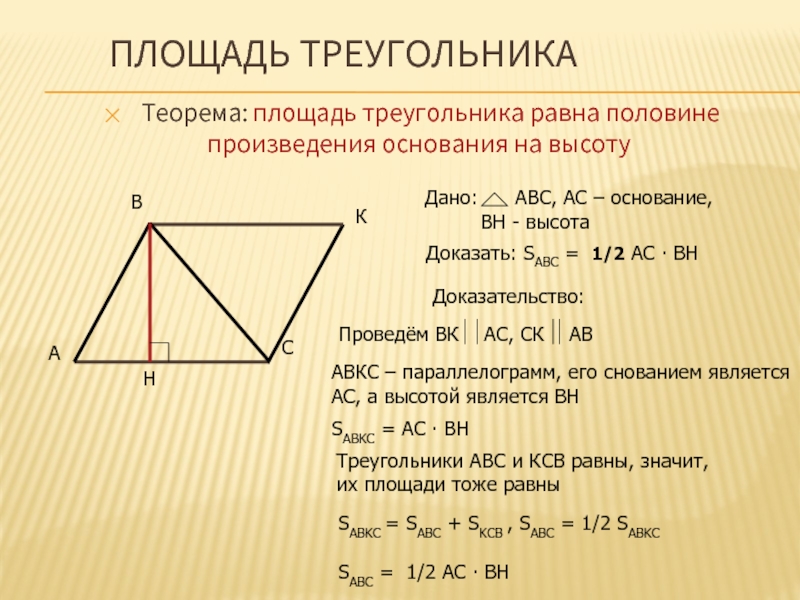
Слайд 4ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Теорема: площадь треугольника равна половине
произведения основания на высоту
Доказать: SABC = 1/2 AC ∙ BH
Доказательство:
АВКС – параллелограмм, его снованием является
АС, а высотой является ВН
SABKC = AC ∙ BH
SABKC = SABC + SKCB , SABC = 1/2 SABKC
SABC = 1/2 AC ∙ BH
Треугольники АВС и КСВ равны, значит,
их площади тоже равны
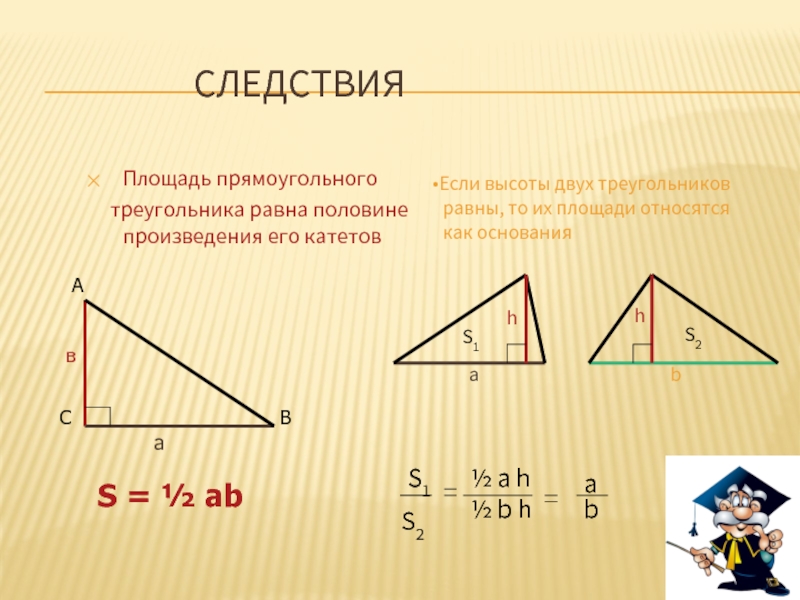
Слайд 5СЛЕДСТВИЯ
Площадь прямоугольного
треугольника равна половине произведения его катетов
S =
½ ab
Если высоты двух треугольников
равны, то их площади относятся
как основания
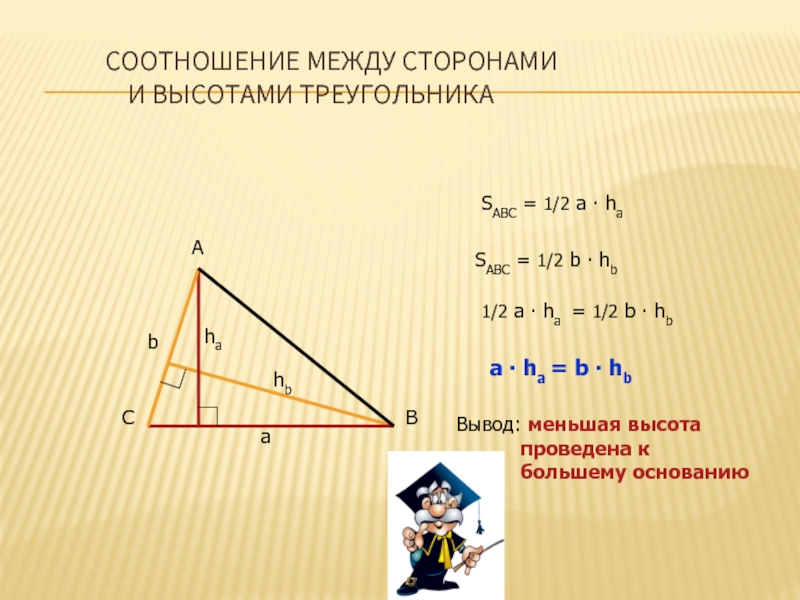
Слайд 6СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ
И ВЫСОТАМИ ТРЕУГОЛЬНИКА
SABC = 1/2 a
∙ ha
SABC = 1/2 b ∙ hb
1/2 a ∙ ha = 1/2 b ∙ hb
a ∙ ha = b ∙ hb
Вывод: меньшая высота
проведена к
большему основанию
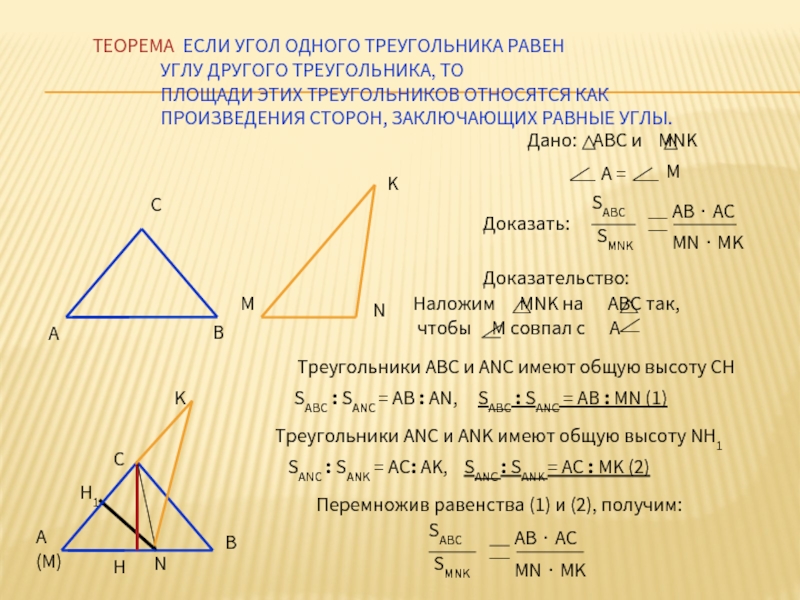
Слайд 7ТЕОРЕМА: ЕСЛИ УГОЛ ОДНОГО ТРЕУГОЛЬНИКА РАВЕН
УГЛУ ДРУГОГО ТРЕУГОЛЬНИКА, ТО
ПЛОЩАДИ ЭТИХ ТРЕУГОЛЬНИКОВ ОТНОСЯТСЯ КАК
ПРОИЗВЕДЕНИЯ СТОРОН, ЗАКЛЮЧАЮЩИХ РАВНЫЕ УГЛЫ.
Доказательство:
Треугольники АВС и АNC имеют общую высоту СН
SABC : SANC = AB : AN, SABC : SANC = AB : MN (1)
Треугольники ANC и ANK имеют общую высоту NH1
SANC : SANK = AС: AK, SANC : SANK = АС : MK (2)
Слайд 9ПЛОЩАДЬ ВСЕГО МНОГОУГОЛЬНИКА РАВНА СУММЕ ПЛОЩАДЕЙ ЕГО ЧАСТЕЙ, НА КОТОРЫЕ ОН
РАЗБИТ НЕКОТОРОЙ ПРЯМОЙ.
Слайд 10ПЛОЩАДЬ КВАДРАТА РАВНА КВАДРАТУ ДЛИНЫ ЕГО СТОРОНЫ, Т.Е. ПЛОЩАДЬ КВАДРАТА СО
СТОРОНОЙ А ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ.
а
S=а2
Слайд 13
ЛИТЕРАТУРА
Интернет
Геометрия. 7-9 классы: учеб. Для общеобразоват . учреждений /Л С Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.) – 19- е изд. – М. : Просвещение, 2009. – 384с.
