- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 9 “Элементы фрактального анализа информационных потоков” презентация
Содержание
- 1. Лекция 9 “Элементы фрактального анализа информационных потоков”
- 2. © ElVisti Понятие «фрактал» Термин
- 3. © ElVisti Фрактальная размерность Феликс
- 4. © ElVisti Примеры абстрактных фракталов
- 5. © ElVisti Фракталы в природе
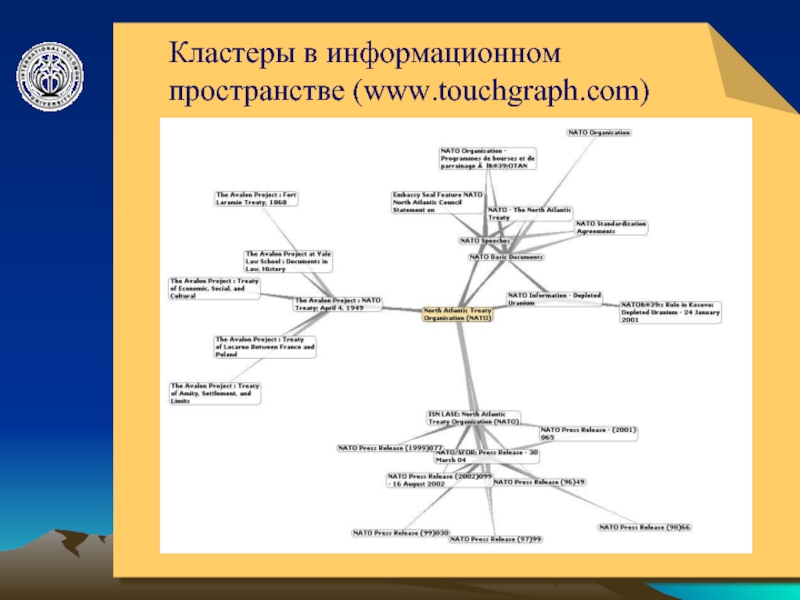
- 6. © ElVisti Кластеры в информационном пространстве (www.touchgraph.com)
- 7. © ElVisti «Дробление» источников по параметрам (www.newsisfree.com)
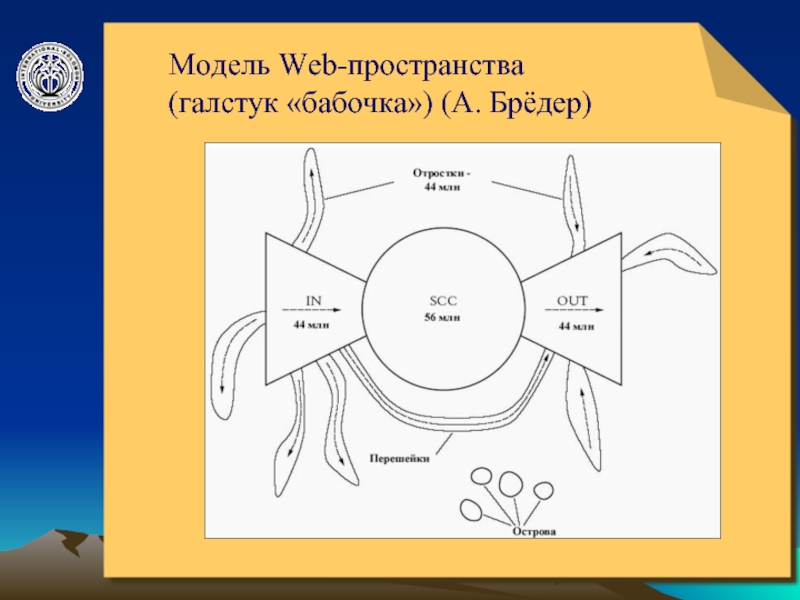
- 8. © ElVisti Модель Web-пространства (галстук «бабочка») (А. Брёдер)
- 9. © ElVisti Фракталы и временные
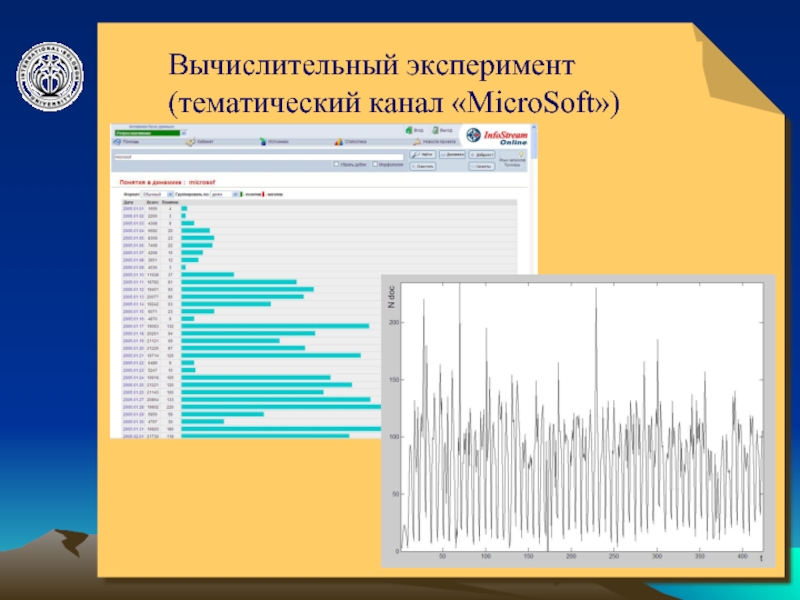
- 10. © ElVisti Вычислительный эксперимент (тематический канал «MicroSoft»)
- 11. © ElVisti Вычислительный эксперимент (расчет
- 12. © ElVisti Спасибо за внимание! Ландэ
Слайд 1© ElVisti
Лекция 9
“Элементы фрактального
анализа
информационных потоков”
Дмитрий Владимирович ЛАНДЭ
МЕЖДУНАРОДНЫЙ СОЛОМОНОВ
Слайд 2© ElVisti
Понятие «фрактал»
Термин фрактал (от латинского
слова fractus – дробный),
Бенуа Мандельбротом в 1975 году
для обозначения нерегулярных
самоподобных математических структур.
"Фракталом называется структура,
состоящая из частей, которые
в каком-то смысле подобны целому"
Множество Мандельброта:
Слайд 3© ElVisti
Фрактальная размерность
Феликс Хаусдорф
Пусть есть множество G в пространстве Rn.
Разобьем пространство Rn на n-мерные кубы
с длиной ребра δ и обозначим число кубов,
необходимых для покрытия ими множества G,
через N(δ). Тогда величина размерности
Хаусдорфа-Безиковича D должна удовлетворять
следующему условию:
Размерность Хаусдорфа-Безиковича
Данное определение можно упростить,
сделав его более удобным для практического
применения. Видно, что при δ ≈ 0, оно
эквивалентно:
D ≈ - ln N(δ) / ln δ.
Слайд 4© ElVisti
Примеры абстрактных фракталов
Участок границы множества Мандельброта
Множество Мандельброта:
Z[i+1] =
где Z и C - комплексные переменные.
IFS представляет собой аффинные преобразования плоскости:
X' = A*X + B*Y + C
Y' = D*X + E*Y + F
"Дракон" Хартера-Хейтуэя
«Снежинка» Коха
Слайд 5© ElVisti
Фракталы в природе
Длина береговой линии L зависит от
L = Λ l1-α,
Λ = const . Для побережья Великобритании α≈ 1.24.
Береговая линия
Рангеоморфы
Организмы, жившие на Земле
575
миллионов лет назад.
Слайд 9© ElVisti
Фракталы и временные ряды.
Показатель Херста
Среднее значение:
Накопившееся отклонение:
Размах:
Стандартное отклонение:
Обнаружено Херстом:
Связь
D + H = 2.
Н – показатель Херста
Слайд 11© ElVisti
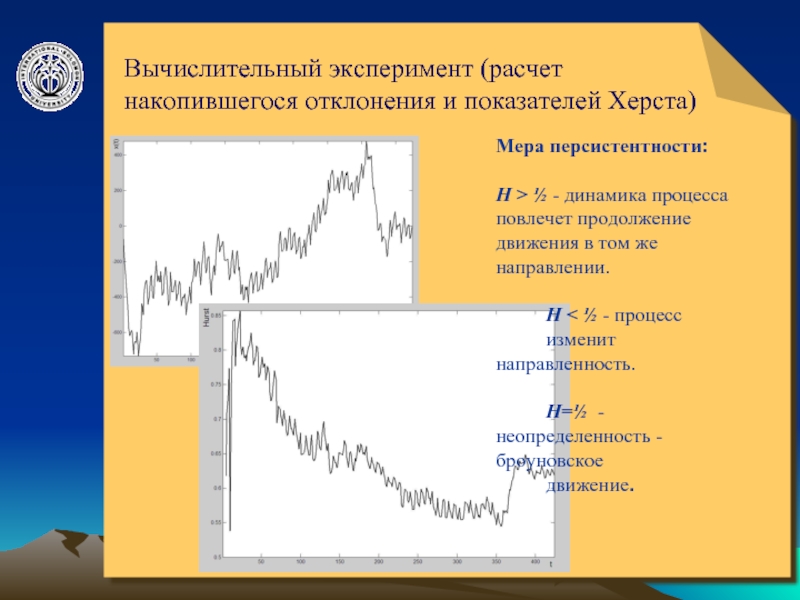
Вычислительный эксперимент (расчет накопившегося отклонения и показателей Херста)
Мера персистентности:
H
H < ½ - процесс изменит направленность.
H=½ - неопределенность - броуновское
движение.



![© ElVisti Примеры абстрактных фракталов Участок границы множества МандельбротаМножество Мандельброта:Z[i+1] = Z[i] * Z[i] +](/img/tmb/1/3387/0ab2ab0e954ce81f2f564e7eeecca9a2-800x.jpg)