Сравнение методов решения обратной задачи восстановления характеристик атмосферы по спутниковым измерениям в ИК диапазоне.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Соколов Антон, Институт Вычислительной Математики РАН, Universite du Littoral Cote d'Opale презентация
Содержание
- 1. Соколов Антон, Институт Вычислительной Математики РАН, Universite du Littoral Cote d'Opale
- 2. Прямая задача: Для заданного состояния системы океан-атмосфера
- 3. dz’ dz’
- 4. Монохроматическое и измеренное излучение
- 5. Статистические данные и выбор каналов измерений.
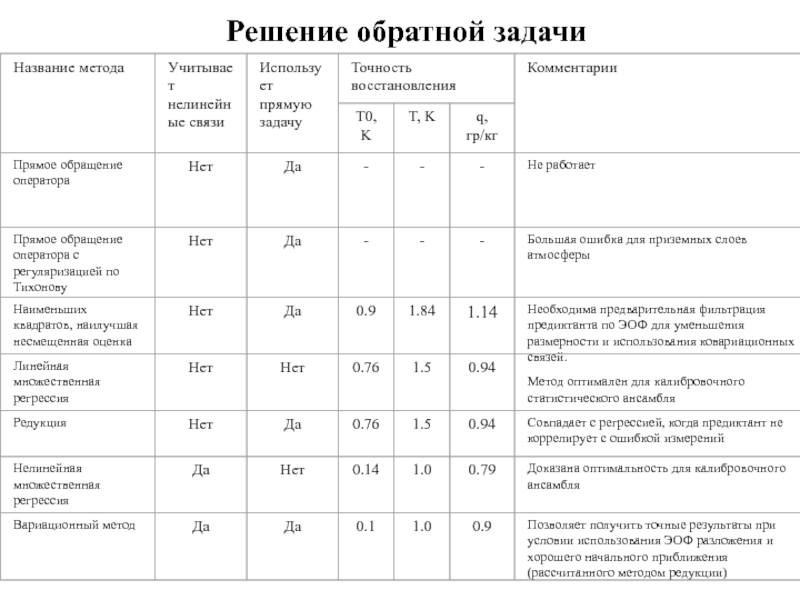
- 6. Решение обратной задачи
- 7. Линейные методы Пусть прямая задача допускает представление:
- 8. Весовые функции
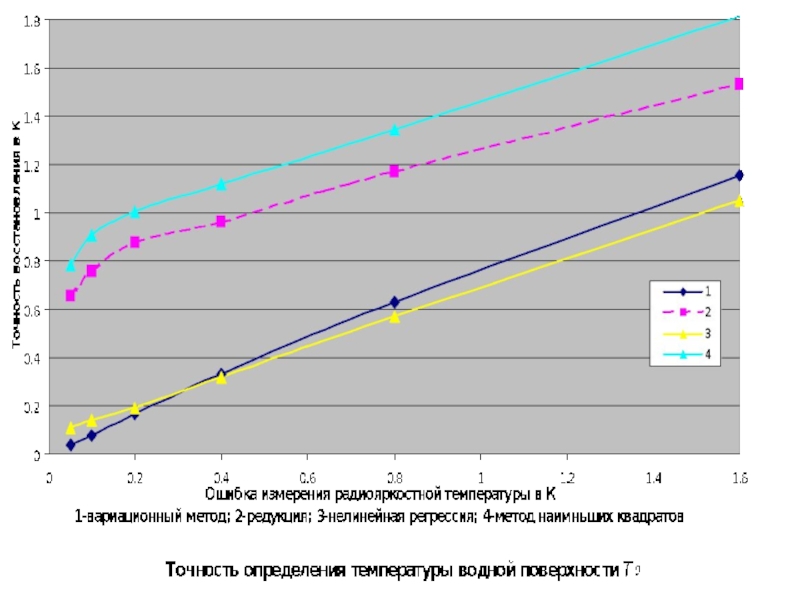
- 9. Метод наилучшей несмещенной оценки Совместный вектор раскладывался
- 10. Метод редукции и регрессии. Для точно вычисленных
- 11. Нелинейная регрессия. + Метод позволяет учесть нелинейные
- 12. Вариационный метод Использовано нулевое приближение полученное
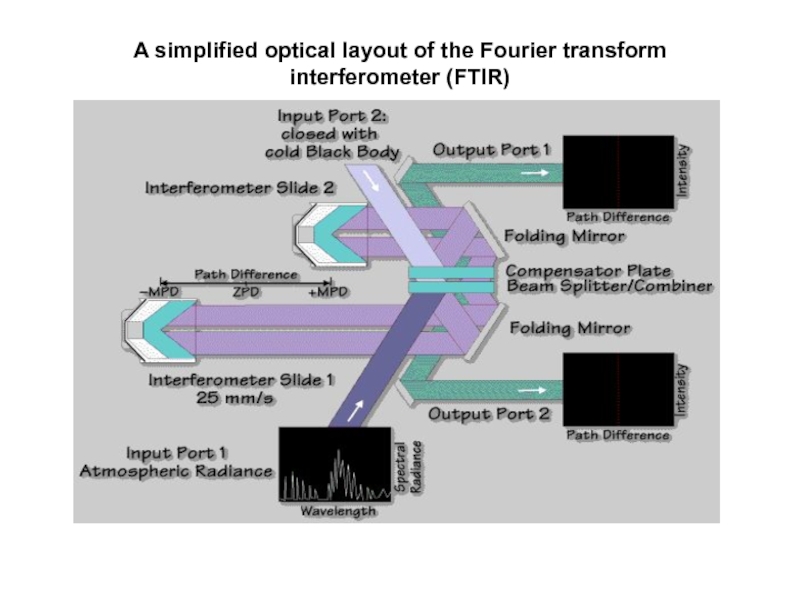
- 19. A simplified optical layout of the Fourier transform interferometer (FTIR)
- 20. Регистрируемый на спутнике сигнал: - спектральная характеристика, - диаграмма направленности
- 21. dz’ h
- 22. Упрощения и предположения. Спектральная и угловая характеристики
- 23. Расчет коэффициента поглощения и учет водяного континуума
- 25. Расчет Якобиана прямой задачи. Явного рассчитан
- 26. Выбор частот измерений Считалось, что измерения
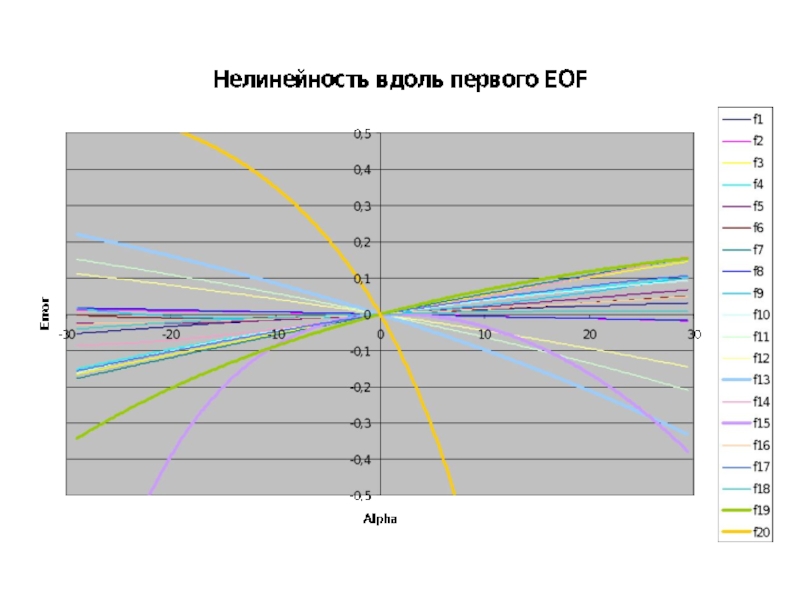
- 27. Оценка нелинейности. Ошибка линеаризации прямой задачи
- 28. Вывод: Нелинейность данной задачи позволяет ожидать удовлетворительных
- 30. Пример точного и приближенного решения некорректной задачи
- 31. Разложение по ЭОФ. Задача восстановления профиля температуры
- 32. Таблица 1. Ошибка восстановления для редукции и нелинейной регрессии.
- 33. Выводы: Редукция дает достаточно точный результат (на
- 34. Модифицированный метод Ньютона
- 35. Ошибка восстановления в точке на первом и
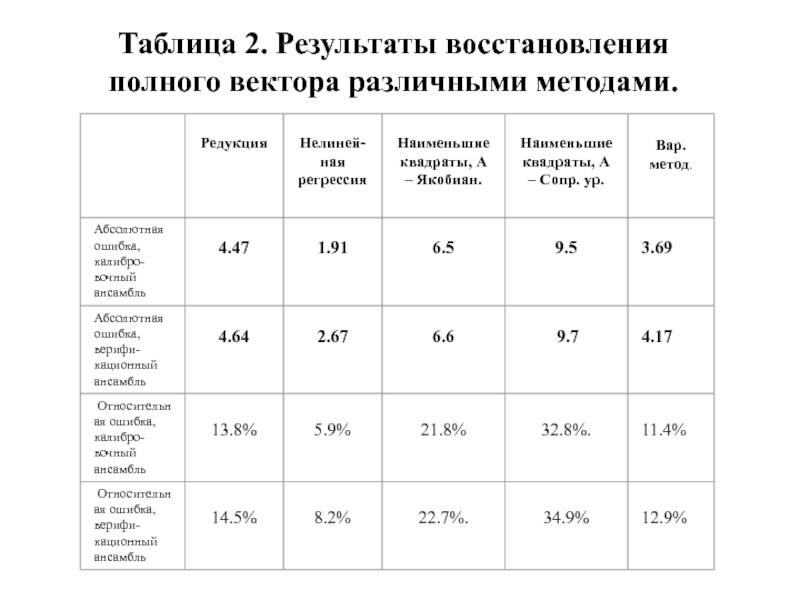
- 36. Таблица 2. Результаты восстановления полного вектора различными методами, относительная ошибка.
- 38. Таблица 3. Результаты восстановления полного вектора различными методами, абсолютная ошибка.
- 39. Исследование на нелинейность. Ошибка линеаризации прямой
- 41. Таблица 2. Результаты восстановления полного вектора различными методами.
- 42. Основные результаты. Решалась задача определения профилей
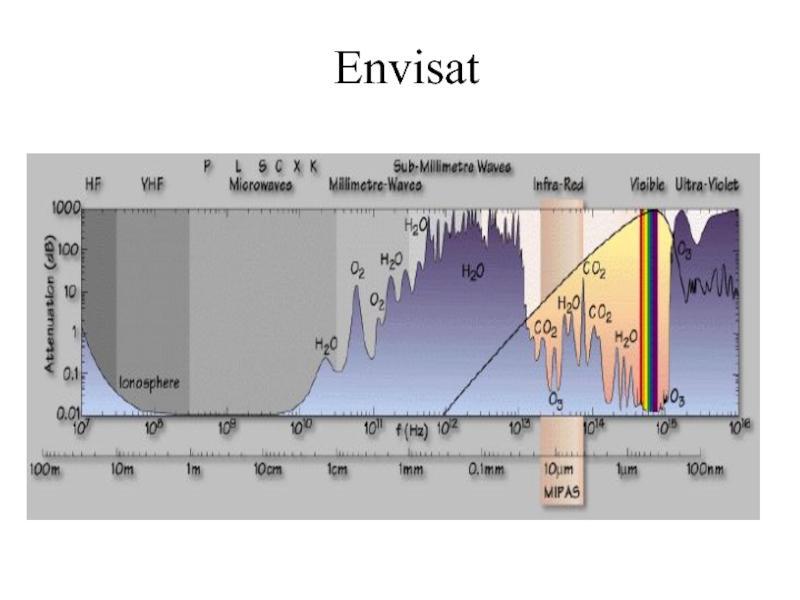
- 43. Envisat
Слайд 1Соколов Антон,
Институт Вычислительной Математики РАН,
Université du Littoral Côte d'Opale
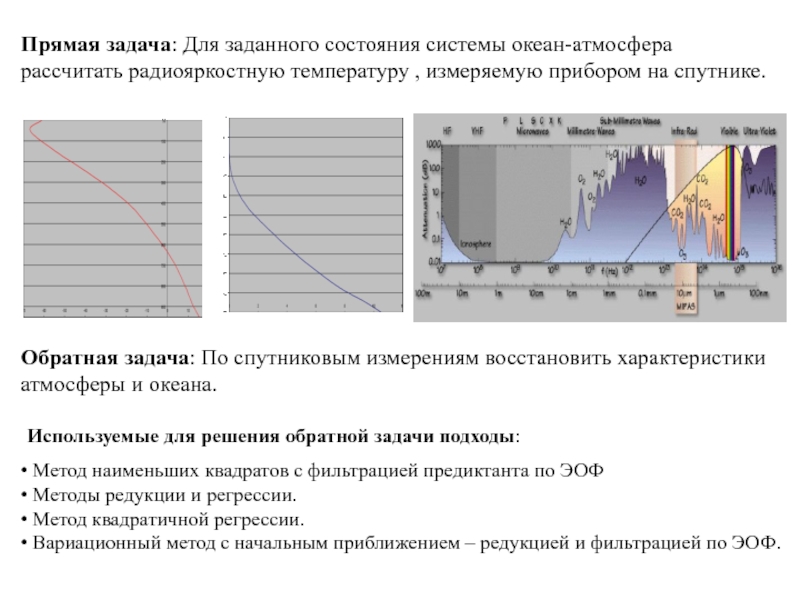
Слайд 2Прямая задача: Для заданного состояния системы океан-атмосфера рассчитать радиояркостную температуру ,
измеряемую прибором на спутнике.
Обратная задача: По спутниковым измерениям восстановить характеристики атмосферы и океана.
Используемые для решения обратной задачи подходы:
Метод наименьших квадратов с фильтрацией предиктанта по ЭОФ
Методы редукции и регрессии.
Метод квадратичной регрессии.
Вариационный метод с начальным приближением – редукцией и фильтрацией по ЭОФ.
Слайд 3dz’
dz’
h
z’
I1
dI2
I3
Спутник
Измеряемый сигнал:
Атмосфера безоблачная, равновесная
Поглощение молекулярное и континуальное
Углы
визирования менее 45 градусов
Параметры атмосферы - являются гладкими функциями высоты
Параметры атмосферы - являются гладкими функциями высоты
Упрощения:
Слайд 5Статистические данные и выбор каналов измерений.
Использован банк данных Европейского Центра
Среднесрочного Прогноза. Выбрано 6000 реализаций, которые разделены на два ансамбля - калибровочный и верификационный.
В некоторых задачах использовалось разложение x по ЭОФ.
Соответствующие статистические данные по сигналам, регистрируемым спутником, были смоделированы:
Выбор частот (измерительных каналов):
Отбор по весовым функциям
Выбор наиболее информативных
Слайд 7Линейные методы
Пусть прямая задача допускает представление:
- отклонение полного вектора от
среднего
Будем искать решение в виде:
R – некоторый линейный оператор.
Далее, где необходимо, считаем x и I несмещенными.
Слайд 9Метод наилучшей несмещенной оценки
Совместный вектор раскладывался по ЭОФ, что позволило восстанавливать
параметры атмосферы, за счет корреляционных связей.
Оптимально использование 7-8 ЭОФ и 10-12 измерений.
Оптимально использование 7-8 ЭОФ и 10-12 измерений.
A - Якобиан,
- отклонение проекции полного вектора на первые ЭОФ, - ков. матрица ошибки.
Точность восстановления: 22%
Слайд 10Метод редукции и регрессии.
Для точно вычисленных ковариационных матриц редукция и регрессия
совпадают, если предиктант не коррелирует с ошибкой.
- ков. и автоков. матрицы.
A – Якобиан, либо оператор полученный методом сопряженных уравнений. Размерность предиктанта – 23, предиктора – 30.
Слайд 11Нелинейная регрессия.
+ Метод позволяет учесть нелинейные связи между предиктором и предиктантом.
+
Получающийся полином оптимален.
Размерность линейной задачи резко возрастает:
K -> (K+1)K/2.
Размерность линейной задачи резко возрастает:
K -> (K+1)K/2.
Слайд 12Вариационный метод
Использовано нулевое приближение полученное редукцией.
Предиктант спроектирован на подпространство первых
ЭОФ (взято 15 векторов).
Использован метод минимизации Ньютона и модифицированный метод Ньютона.
Использован метод минимизации Ньютона и модифицированный метод Ньютона.
x - восстанавливаемый вектор, - априорная оценка восстанавливаемого вектора,
- измерение , - прямая задача (1). Размерность вектора измерений - 20.
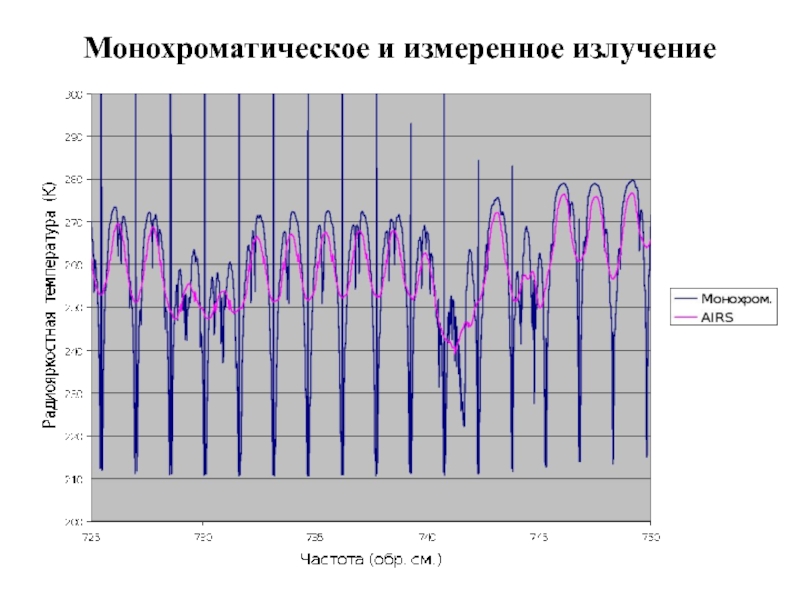
Слайд 20Регистрируемый на спутнике сигнал:
- спектральная характеристика, -
диаграмма направленности
Слайд 21
dz’
h
z’
I1
dI2
dI3
Surface
Satellite
(1)
- коэффициент поглощения
- коэффициент отражения
- излучательная способность
поверхности
- функция Планка
- Закон Кирхгоффа
Слайд 22Упрощения и предположения.
Спектральная и угловая характеристики прибора дельта-функции.
Измерения проводятся не слишком
больших углах. Тогда можно пренебречь кривизной поверхности.
Поглощение только молекулярное и континуальное.
Поглощение только молекулярное и континуальное.
4. Существует некоторое среднее состояние атмосферы и реализации распределены около этого состояния.
5. Профили температуры и влажности являются достаточно гладкими функциями высоты и задача может быть дискретизирована.
Слайд 23Расчет коэффициента поглощения и учет водяного континуума
Молекулярное поглощение рассчитывалось методом
полинейного счета, с использованием спектроскопической БД HITRAN.
Была добавлена параметризация континуального поглощения водным паром, создатель Clough S.A.
Были аналитически рассчитаны производные поглощения по температуре, давлению и концентрации.
Была добавлена параметризация континуального поглощения водным паром, создатель Clough S.A.
Были аналитически рассчитаны производные поглощения по температуре, давлению и концентрации.
Слайд 25Расчет Якобиана прямой задачи.
Явного рассчитан Якобиан прямой задачи, что позволило:
1.
Оценить нелинейность задачи.
2. Решать обратную задачу методом редукции и методом наилучшей линейной несмещенной оценки с использованием Якобиана.
3. Использовать метод минимизации Ньютона и модифицированный метод Ньютона для нахождения решения обратной задачи вариационным методом.
2. Решать обратную задачу методом редукции и методом наилучшей линейной несмещенной оценки с использованием Якобиана.
3. Использовать метод минимизации Ньютона и модифицированный метод Ньютона для нахождения решения обратной задачи вариационным методом.
Слайд 26Выбор частот измерений
Считалось, что измерения проводятся в надир,
Было выбрано
60 частот в полосах CO2 и H2O, на которых излучение несет информацию с различных высот от 0 до h.
Частоты были отсортированы по убыванию информативности.
Частоты были отсортированы по убыванию информативности.
Слайд 27Оценка нелинейности.
Ошибка линеаризации прямой задачи для векторов из ансамбля:
(3)
- решение прямой задачи (1)
- линеаризованное решение, A - матрица Якоби,
Слайд 28Вывод: Нелинейность данной задачи позволяет ожидать удовлетворительных результатов от линейных методов.
По видимому, нелинейные методы позволят повысить точность решения обратной задачи.
(4)
Проверка нелинейности для каждой частоты при отклонениях от среднего профиля вдоль первых ЭОФ:
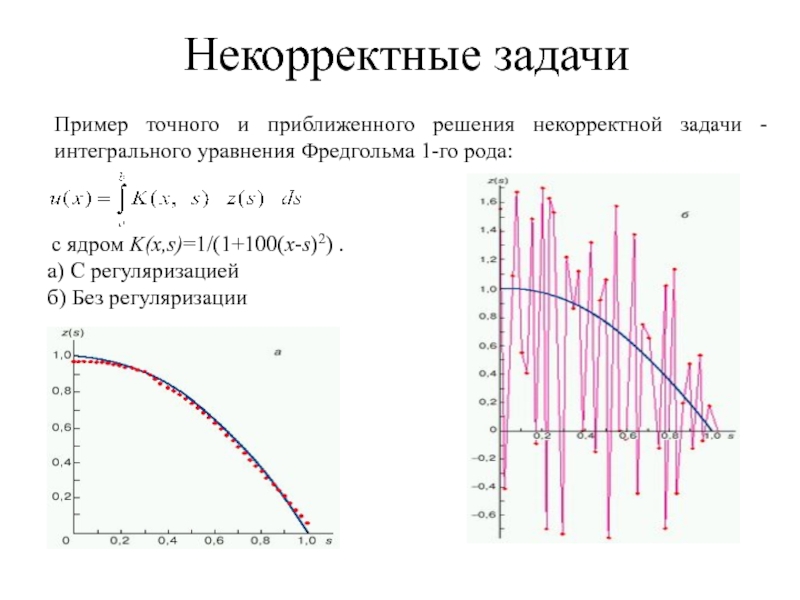
Слайд 30Пример точного и приближенного решения некорректной задачи - интегрального уравнения Фредгольма
1-го рода:
Некорректные задачи
с ядром K(x,s)=1/(1+100(x-s)2) .
а) С регуляризацией
б) Без регуляризации
Слайд 31Разложение по ЭОФ.
Задача восстановления профиля температуры при фиксированной влажности крайне чувствительна
к влажности и наоборот, поэтому расщепить задачу на две не удается.
Обратную задачу не удалось решить без привлечения ансамбля статистических данных – недостаточно информации о нижних слоях атмосферы (ниже 850 мБар).
Обратную задачу не удалось решить без привлечения ансамбля статистических данных – недостаточно информации о нижних слоях атмосферы (ниже 850 мБар).
- автоковариационная матрица.
Слайд 33Выводы:
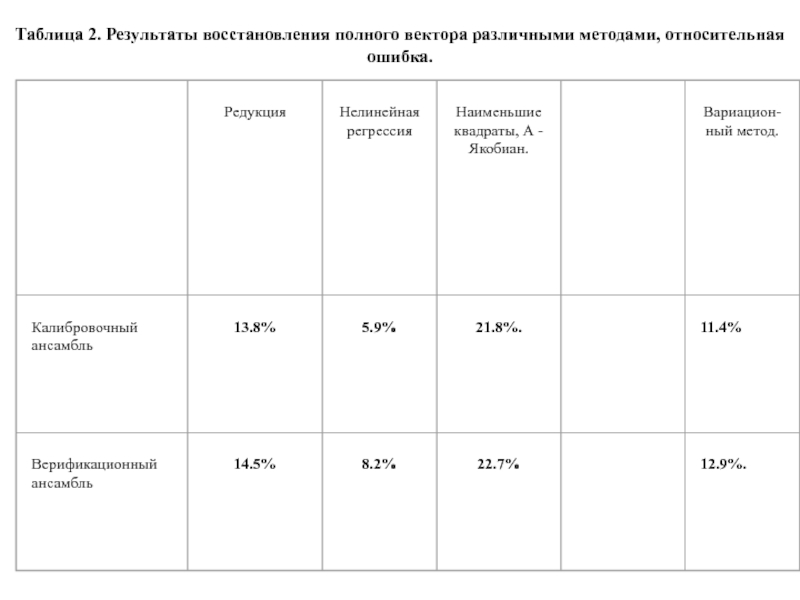
Редукция дает достаточно точный результат (на данных статистических ансамблях)
Нелинейная (квадратичная) регрессия
позволяет значительно повысить точность восстановления.
Однако, нелинейная регрессия значительно более чувствительна к статистическим характеристикам ансамбля и точности измерения.
Однако, нелинейная регрессия значительно более чувствительна к статистическим характеристикам ансамбля и точности измерения.
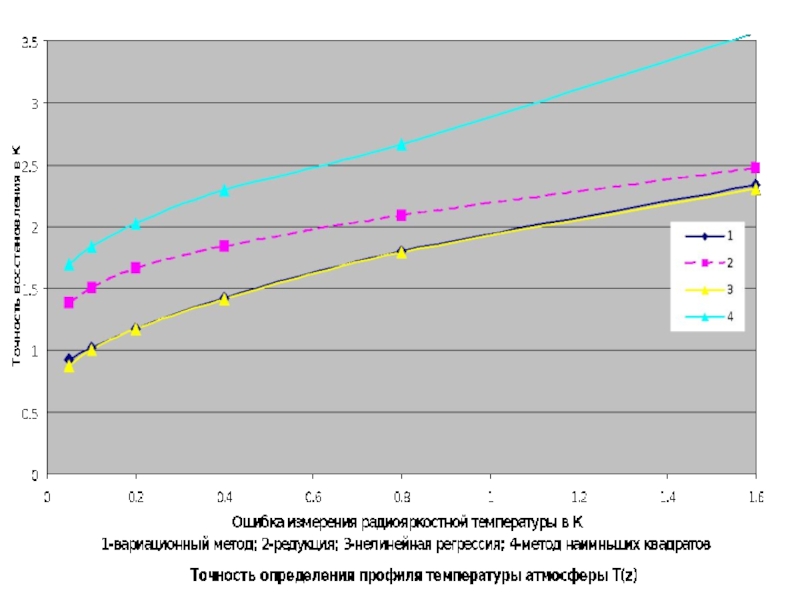
Слайд 35 Ошибка восстановления в точке на первом и втором ансамбле соответственно 11.36%
и 12.98%.
Вывод – результат, полученный методом редукции удалось уточнить вариационным методом.
Вывод – результат, полученный методом редукции удалось уточнить вариационным методом.
Слайд 36Таблица 2. Результаты восстановления полного вектора различными методами, относительная ошибка.
Слайд 38Таблица 3. Результаты восстановления полного вектора различными методами, абсолютная ошибка.
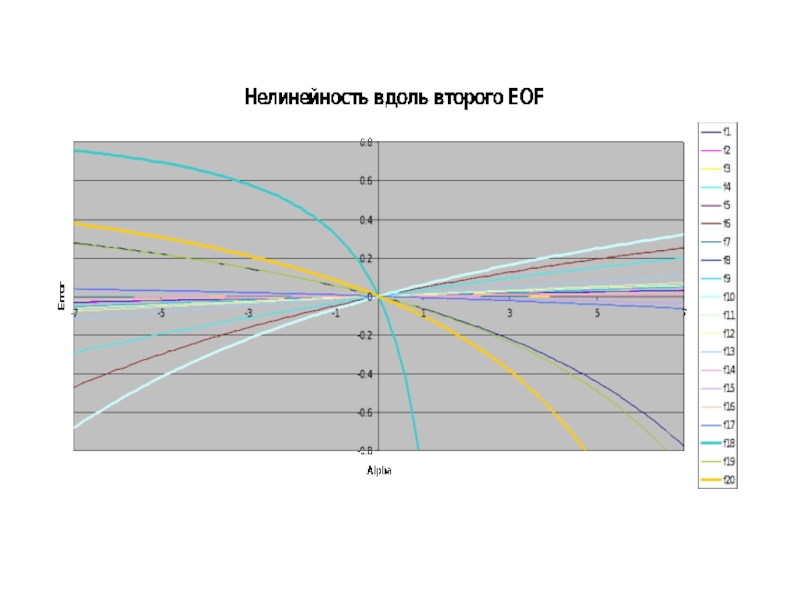
Слайд 39Исследование на нелинейность.
Ошибка линеаризации прямой задачи для векторов из ансамбля:
(3)
- решение прямой задачи (2)
- линеаризованное решение, A - матрица Якоби,
Проверка нелинейности при отклонениях от среднего профиля вдоль первых двух ЭОФ:
(4)
Слайд 42Основные результаты.
Решалась задача определения профилей температуры и влажности атмосферы и
температуры поверхности океана по спутниковым измерениям в ИК диапазоне, при отсутствии рассеяния.
Результаты:
Решена прямая задача с учетом континуального поглощения и отражения от поверхности.
Явно вычислен Якобиан прямой задачи.
Предложена методика выбора измерительных каналов (частот) .
Проведено исследование задачи на нелинейность.
Проведены численные эксперименты решения обратной задачи различными способами:
а) Методом наилучшей несмещенной оценки.
б) Редукцией.
в) Нелинейной регрессией
г) Вариационным методом
Результаты:
Решена прямая задача с учетом континуального поглощения и отражения от поверхности.
Явно вычислен Якобиан прямой задачи.
Предложена методика выбора измерительных каналов (частот) .
Проведено исследование задачи на нелинейность.
Проведены численные эксперименты решения обратной задачи различными способами:
а) Методом наилучшей несмещенной оценки.
б) Редукцией.
в) Нелинейной регрессией
г) Вариационным методом
