- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства равнобедренного треугольника презентация
Содержание
- 1. Свойства равнобедренного треугольника
- 2. Что такое периметр? Сформулируйте 1 признак равенства треугольников. ?
- 3. Повторение: Какой отрезок называется медианой? сколько медиан имеет треугольник? ?
- 4. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
- 5. Какой отрезок называется биссектрисой?
- 6. Отрезок биссектрисы угла треугольника, соединяющий вершину
- 7. Какой отрезок называется высотой? Сколько высот
- 8. Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
- 9. Треугольник, две все стороны которого равны, называется равнобедренным основание Боковая сторона Боковая сторона
- 10. △ABC – равнобедренный, так как AB =
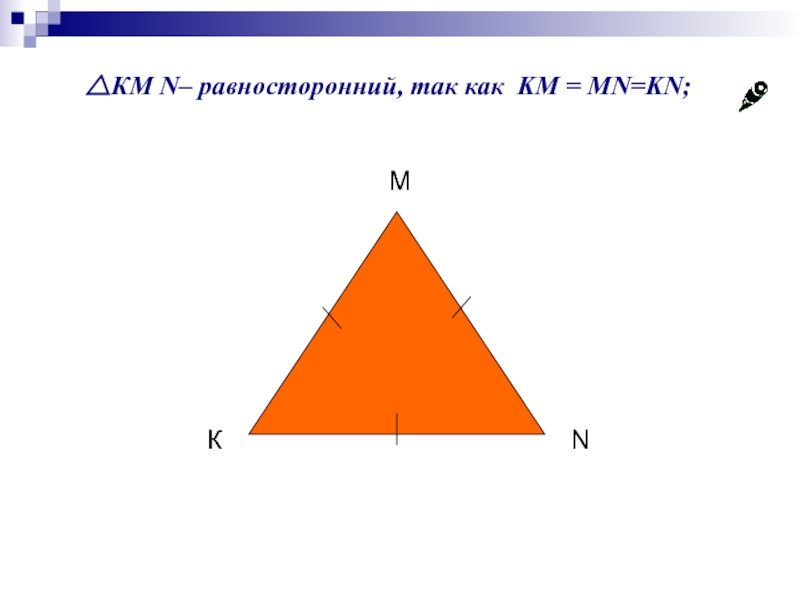
- 11. Треугольник, все стороны которого равны, называется равносторонним
- 12. △КМ N– равносторонний, так как KM = MN=KN; К М N
- 13. «Свойства равнобедренного треугольника» Практическая работа
- 14. В равнобедренном треугольнике углы
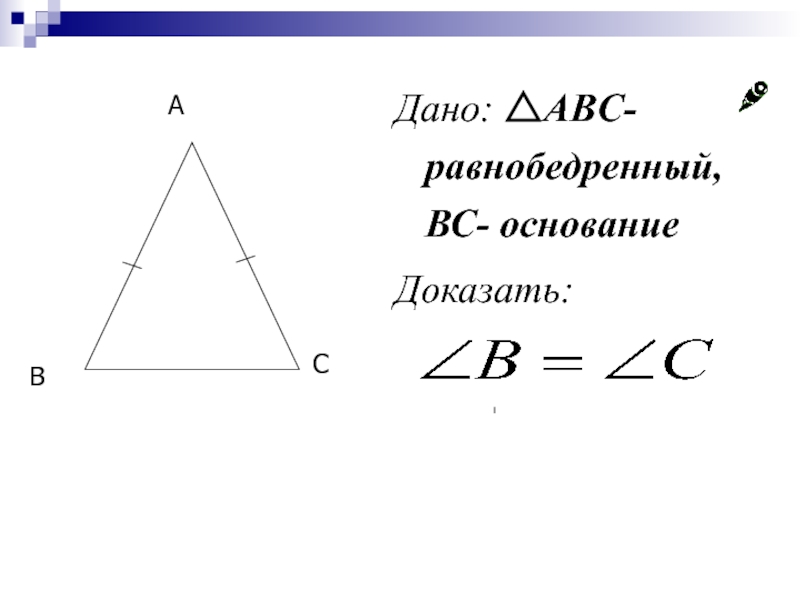
- 15. Дано: △ABC-равнобедренный, ВС- основание Доказать: B C A
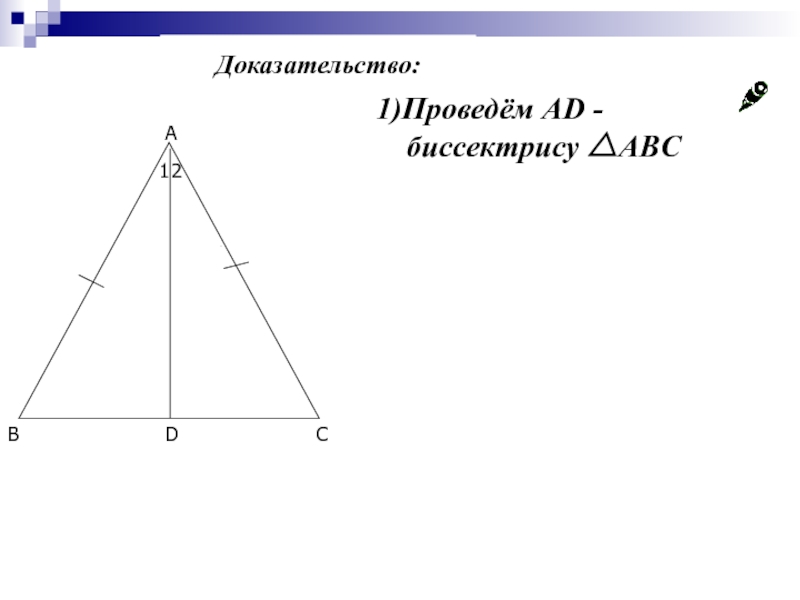
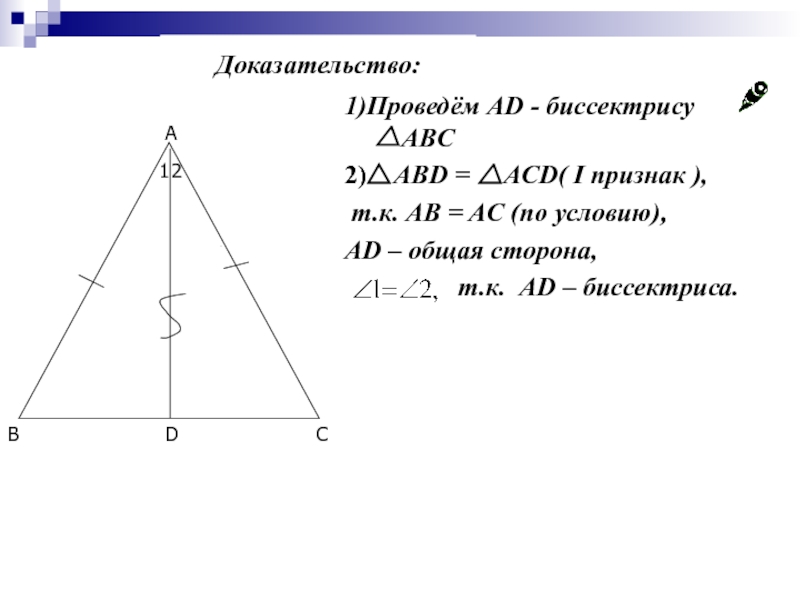
- 16. 1)Проведём AD - биссектрису △ABC Доказательство:
- 17. 1)Проведём AD - биссектрису △ABC 2)△ABD =
- 18. 1)Проведём AD - биссектрису △ABC 2)△ABD =
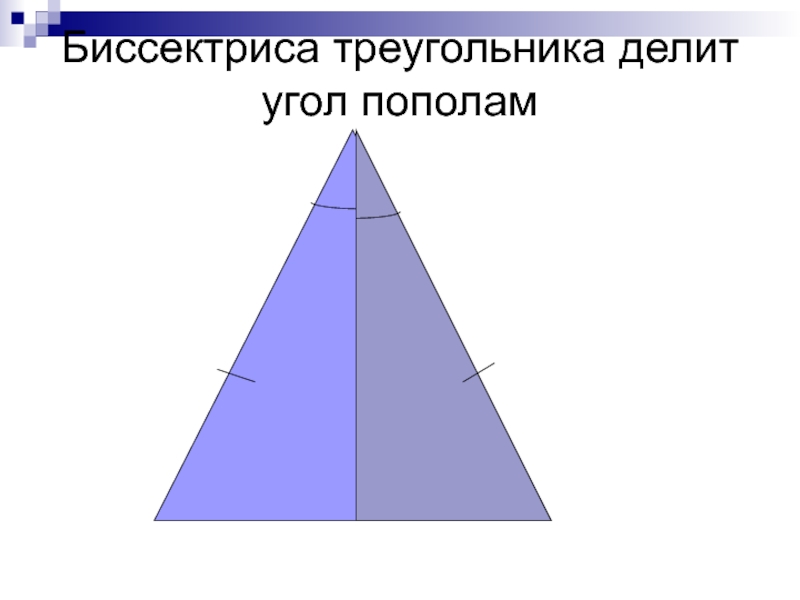
- 19. Биссектриса треугольника делит угол пополам
- 20. В равнобедренном треугольнике биссектриса, проведенная к основанию,
- 21. 2 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА Дано:
- 22. Самостоятельная работа Вариант I
- 23. Медиана равнобедренного треугольника, проведенная к
- 24. Равнобедренные и равносторонние треугольники в жизни
- 25. КРЫШИ ДОМОВ И БАШЕН
- 26. ПАКЕТ С МОЛОКОМ
- 27. ЕГИПЕТСКИЕ ПИРАМИДЫ
- 28. СЕВЕРНЫЕ РОСПИСИ
- 29. ПАБЛО ПИКАССО «ВИНСЕНТ ВАН ГОГ»
- 30. Домашнее задание: § 18, вопросы 10-13
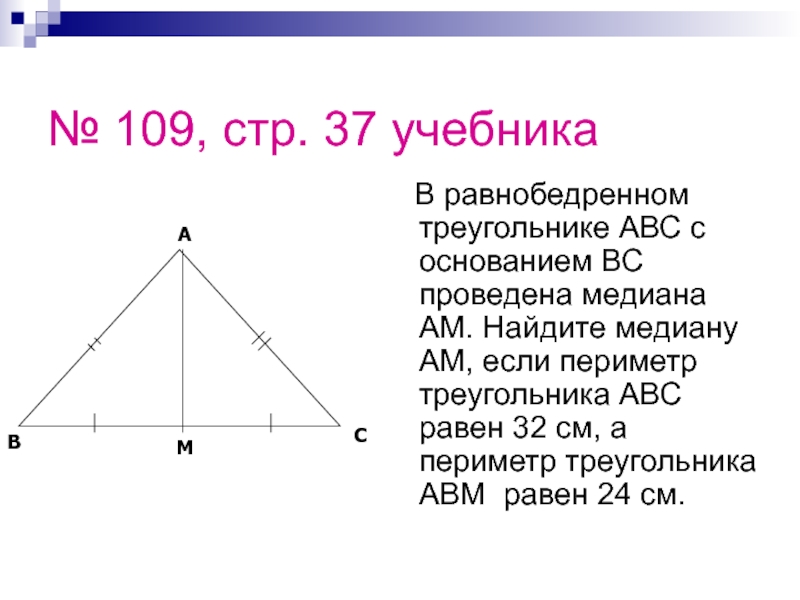
- 31. № 109, стр. 37 учебника
- 32. № 109, стр. 37 учебника ABC –
- 33. № 109, стр. 37 учебника △ ABC
- 34. Тест «Свойства равнобедренного треугольника»
- 35. Тест «Свойства равнобедренного треугольника»
- 36. № 113 Точки M и P
- 37. №107 Самостоятельно
- 38. Спасибо за урок!
Что такое периметр? Сформулируйте 1 признак равенства треугольников. ?
Слайд 4Отрезок, соединяющий
вершину треугольника с серединой противоположной
стороны, называется
медианой треугольника
Слайд 5
Какой отрезок называется биссектрисой?
Сколько биссектрис имеет треугольник?
Какой отрезок называется
биссектрисой?
Сколько биссектрис имеет треугольник?
Сколько биссектрис имеет треугольник?
?
Слайд 6Отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с
точкой противоположной
стороны,
называется
биссектрисой треугольника
Слайд 7
Какой отрезок называется высотой?
Сколько высот имеет треугольник?
Какой отрезок называется высотой?
Сколько высот
имеет треугольник?
?
Слайд 8Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную
сторону, называется
высотой треугольника
Слайд 9Треугольник, две все стороны которого равны, называется равнобедренным
основание
Боковая сторона
Боковая сторона
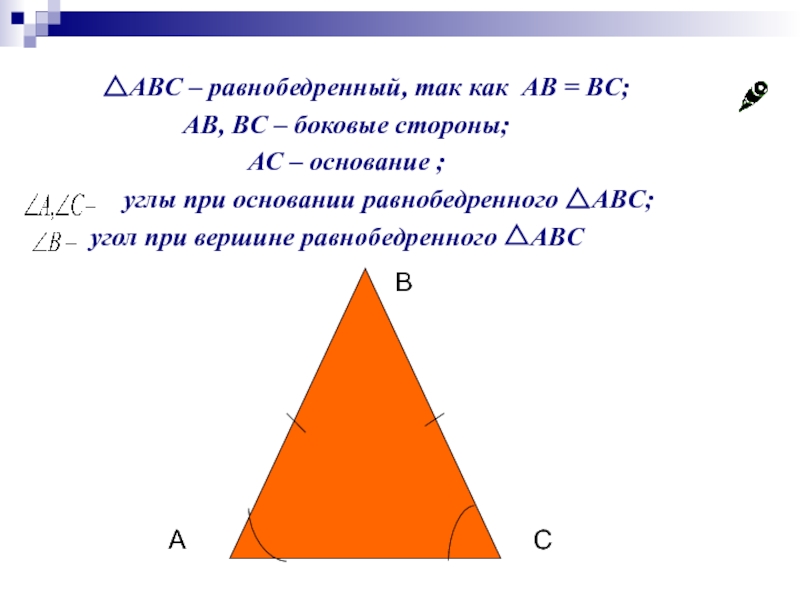
Слайд 10 △ABC – равнобедренный, так как AB = BC;
AB, BC –
боковые стороны;
AС – основание ;
углы при основании равнобедренного △ABC;
угол при вершине равнобедренного △ABC
AС – основание ;
углы при основании равнобедренного △ABC;
угол при вершине равнобедренного △ABC
В
С
А
Слайд 14 В равнобедренном треугольнике углы
при основании равны
Теорема:
1 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Слайд 171)Проведём AD - биссектрису △ABC
2)△ABD = △ACD( I признак ),
т.к.
AB = AC (по условию),
AD – общая сторона,
т.к. АD – биссектриса.
AD – общая сторона,
т.к. АD – биссектриса.
Доказательство:
Слайд 181)Проведём AD - биссектрису △ABC
2)△ABD = △ACD( I признак ),
т.к.
AB = AC (по условию),
AD – общая сторона,
т.к. АD – биссектриса.
3)В равных треугольниках против равных сторон лежат равные углы, поэтому
AD – общая сторона,
т.к. АD – биссектриса.
3)В равных треугольниках против равных сторон лежат равные углы, поэтому
Доказательство:
Слайд 20 В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
Теорема:
2
СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
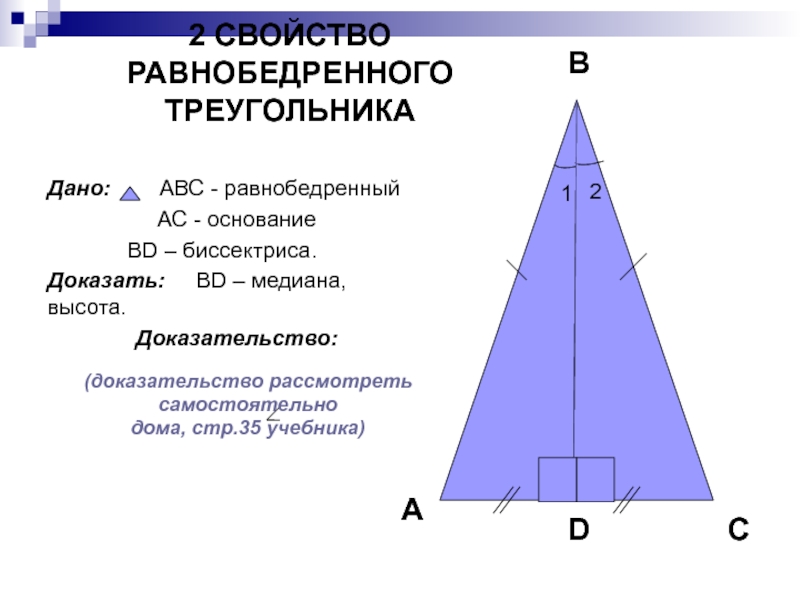
Слайд 212 СВОЙСТВО РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Дано: АВС - равнобедренный
АС
- основание
ВD – биссектриса.
Доказать: ВD – медиана, высота.
Доказательство:
ВD – биссектриса.
Доказать: ВD – медиана, высота.
Доказательство:
А
В
D
С
(доказательство рассмотреть
самостоятельно
дома, стр.35 учебника)
Слайд 22Самостоятельная работа
Вариант I
Исследуйте медианы равнобедренного треугольника и перечислите все
их особенности и свойства.
Вариант II
Исследуйте высоты равнобедренного треугольника и перечислите их особенности и свойства.
Слайд 23 Медиана равнобедренного треугольника, проведенная к основанию, является высотой и
биссектрисой
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой
Слайд 30Домашнее задание:
§ 18, вопросы 10-13 (стр. 50)
№ 108, № 112
Привести пример
применения равнобедренных и равносторонних треугольников в жизни
(творчески оформить)
(творчески оформить)
Слайд 31№ 109, стр. 37 учебника
В равнобедренном треугольнике АВС с
основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см.
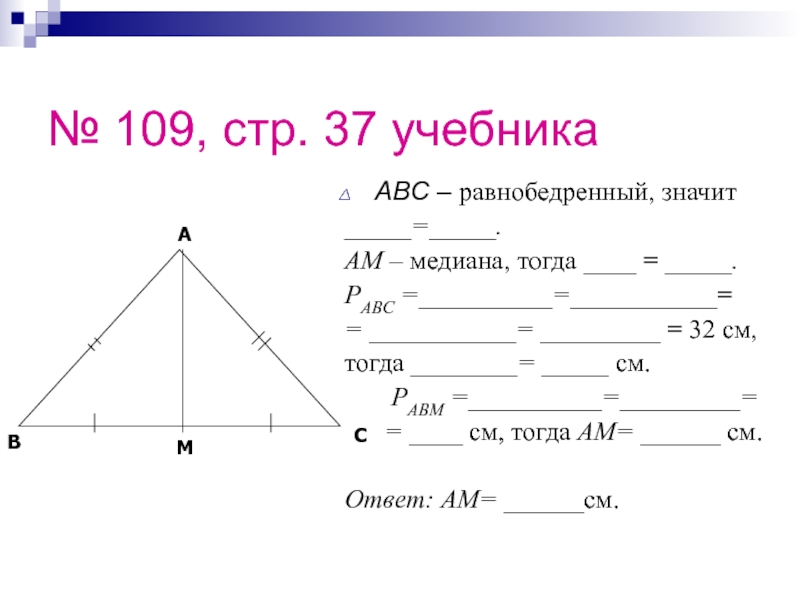
Слайд 32№ 109, стр. 37 учебника
ABC – равнобедренный, значит
_____=_____.
AM – медиана,
тогда ____ = _____.
PABC =__________=___________=
= ___________= _________ = 32 см,
тогда ________= _____ см.
PABM =__________=_________=
= ____ см, тогда AM= ______ см.
Ответ: AM= ______см.
PABC =__________=___________=
= ___________= _________ = 32 см,
тогда ________= _____ см.
PABM =__________=_________=
= ____ см, тогда AM= ______ см.
Ответ: AM= ______см.
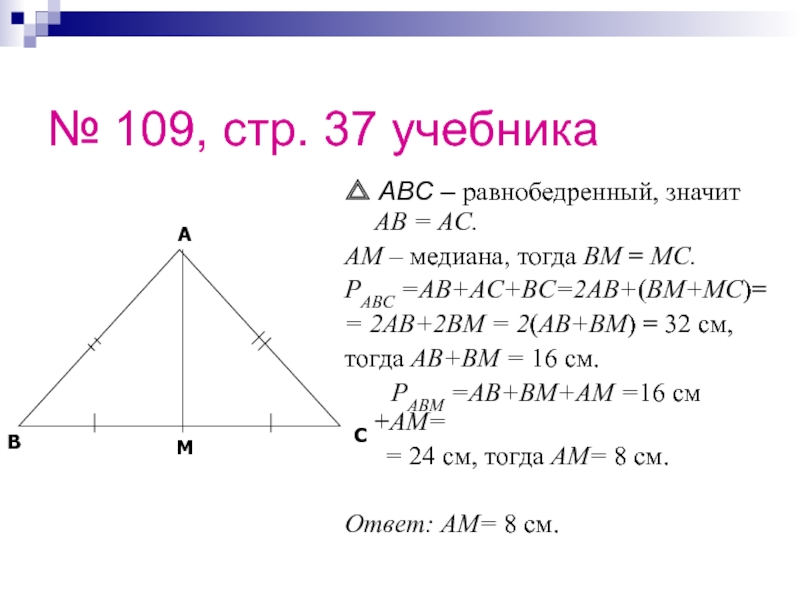
Слайд 33№ 109, стр. 37 учебника
△ ABC – равнобедренный, значит AB =
AC.
AM – медиана, тогда BM = MC.
PABC =AB+AC+BC=2AB+(BM+MC)=
= 2AB+2BM = 2(AB+BM) = 32 см,
тогда AB+BM = 16 см.
PABM =AB+BM+AM =16 см +AM=
= 24 см, тогда AM= 8 см.
Ответ: AM= 8 см.
AM – медиана, тогда BM = MC.
PABC =AB+AC+BC=2AB+(BM+MC)=
= 2AB+2BM = 2(AB+BM) = 32 см,
тогда AB+BM = 16 см.
PABM =AB+BM+AM =16 см +AM=
= 24 см, тогда AM= 8 см.
Ответ: AM= 8 см.
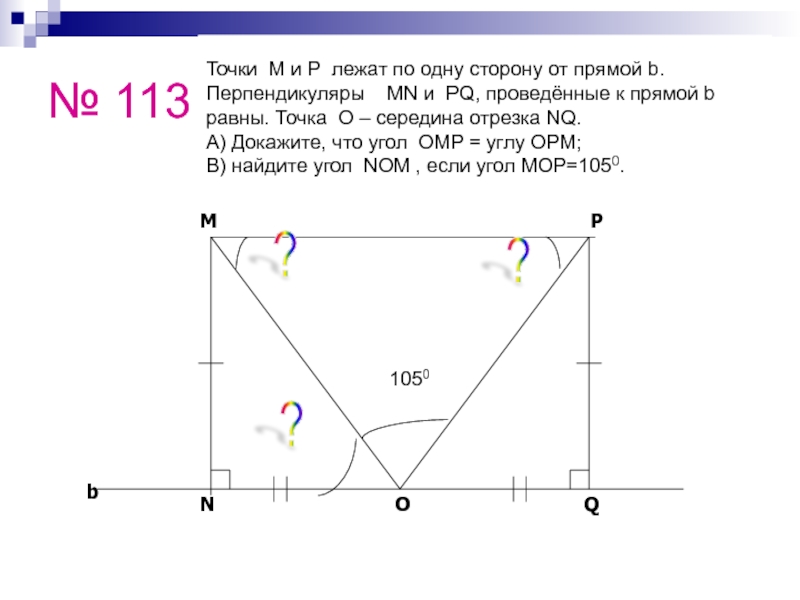
Слайд 36№ 113
Точки M и P лежат по одну сторону от
прямой b.
Перпендикуляры MN и PQ, проведённые к прямой b
равны. Точка O – середина отрезка NQ.
А) Докажите, что угол OMP = углу OPM;
В) найдите угол NOM , если угол MOP=1050.
Перпендикуляры MN и PQ, проведённые к прямой b
равны. Точка O – середина отрезка NQ.
А) Докажите, что угол OMP = углу OPM;
В) найдите угол NOM , если угол MOP=1050.
?
?
1050
?
