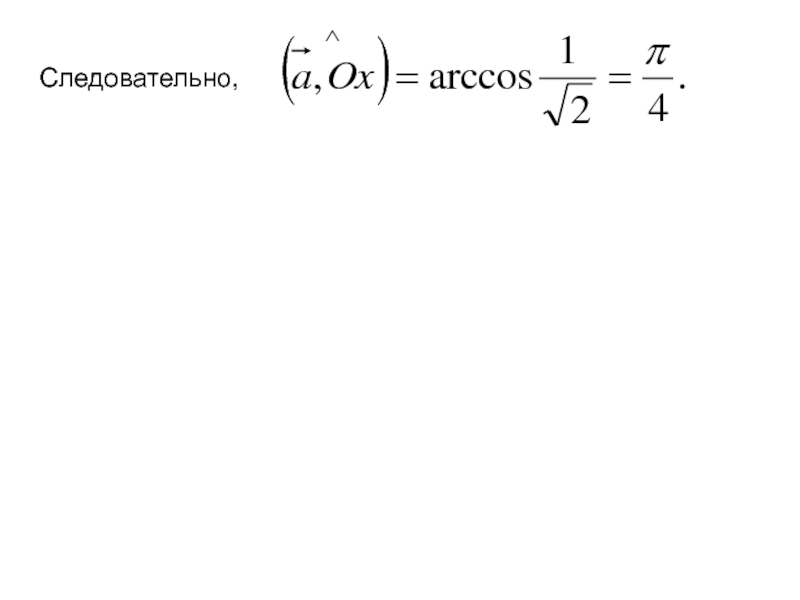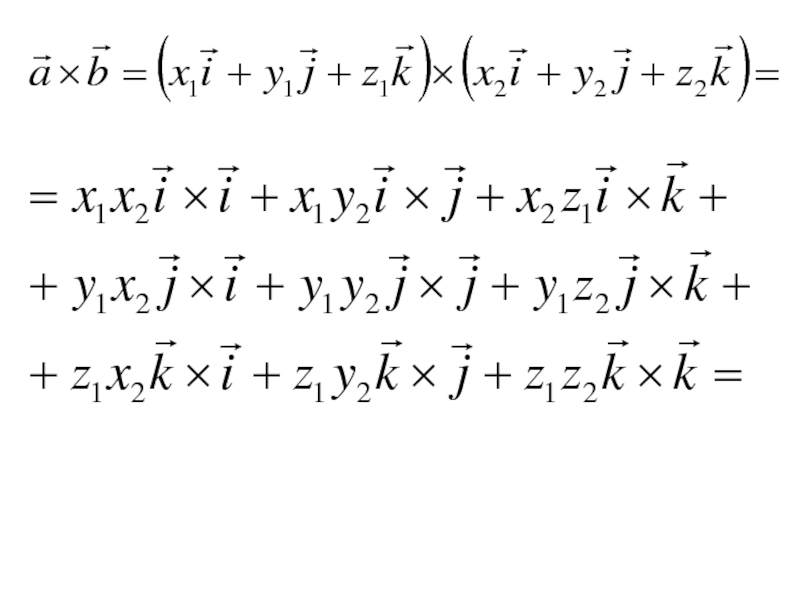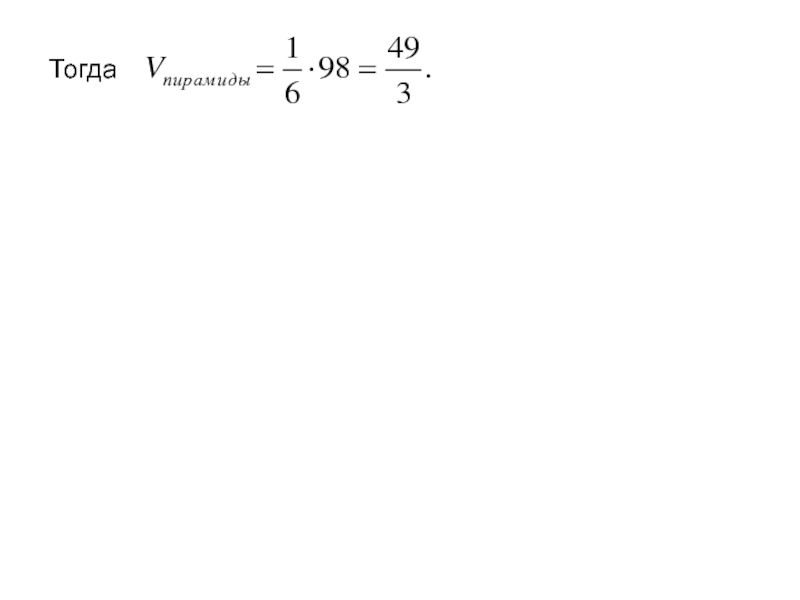- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Глава 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. презентация
Содержание
- 1. Глава 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.
- 2. §1. Векторы. Основные определения. Величины, которые полностью
- 3. Вектором называется направленный отрезок, т.е. отрезок, имеющий
- 4. Вектор, длина которого равна нулю, называется нулевым
- 5. Векторы и
- 6.
- 7. Два вектора называются равными, если они
- 8. Вектор можно переносить в любую точку пространства
- 9.
- 10. §2. Линейные операции над векторами. Под линейными
- 11. б) вектор коллинеарен
- 12. Сумму двух векторов можно находить либо по
- 14. Правило параллелограмма. Пусть
- 16. Сумму трех и более векторов можно находить
- 17. Разностью двух векторов и
- 19. Отметим, что в параллелограмме, построенном на векторах
- 20. Линейные операции над векторами обладают следующими свойствами:
- 21. 3. Прибавление нулевого вектора к любому вектору
- 22. 7. Умножение вектора на число дистрибутивно по
- 23. §3. Проекция вектора на ось. Осью
- 24. Углом между вектором или равным ему
- 25.
- 26. Проекцией вектора на
- 27. Геометрически проекция вектора
- 28. Рис.1 Рис.2
- 29. 1. При умножении вектора на число
- 30. §4. Базис. Разложение вектора по базису. Координаты
- 31.
- 32. Базисом в пространстве называют любые три некомпланарных
- 33. При этом коэффициенты
- 34. 2. При сложении (вычитании) векторов
- 35. 4. Вектор равен
- 37.
- 38. Прямая ОX называется осью абсцисс, прямая ОY
- 39. Базис называют ортонормированным, если базисные векторы попарно
- 40.
- 41. Пусть в прямоугольной системе координат даны две
- 42.
- 43. Учитывая, что при вычитании
- 44. А длина вектора
- 45. Отметим, что в прямоугольной системе координаты вектора
- 46.
- 47. Пусть даны точки и
- 48. Тогда координаты точки М вычисляются
- 49. При точка
- 50. Пример. Даны три последовательные вершины параллелограмма
- 52. Для нахождения координат точки
- 53. §6. Скалярное произведение векторов. Углом между двумя
- 54.
- 55. Скалярным произведением двух векторов называется число, равное
- 56. Скалярное умножение обладает следующими свойствами. 1.
- 57. 3. Скалярное произведение равно нулю, если сомножители
- 58. Пример 1. Найти длину вектора
- 59. Пример 2. Найти угол между векторами
- 60. Пример 3. Вычислить скалярное произведение
- 61. Пусть в прямоугольной системе координат векторы заданы
- 62. Приложения скалярного произведения в геометрии. 1. Проекция
- 63. Поэтому или Таким
- 64. 2. Угол между векторами. Из определения
- 65. 3. Направляющие косинусы векторов. Направление вектора
- 66. Таким образом, Направляющие косинусы связаны соотношением
- 67. Косинусы углов, образованных вектором и осями координат
- 68. Пример. Даны вершины треугольника
- 69. Пример. Вычислить угол между вектором
- 70. Следовательно,
- 71. §7. Векторное произведение векторов. Упорядоченная тройка некомпланарных
- 72. Правая система координат Левая система координат
- 73. Векторным произведением векторов и
- 74.
- 75. Свойства векторного произведения: 1) От перестановки множителей
- 76. 4) 5)
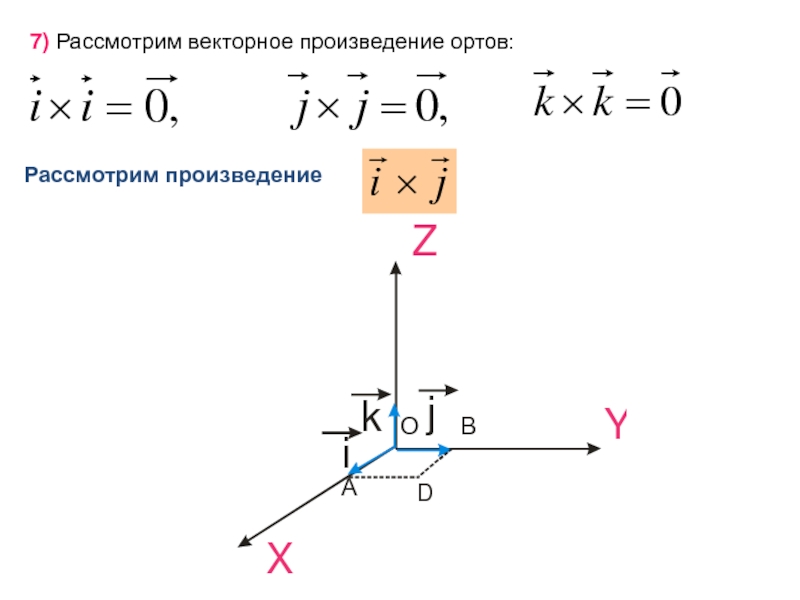
- 77. 7) Рассмотрим векторное произведение ортов:
- 78. Параллелограмм, построенный на
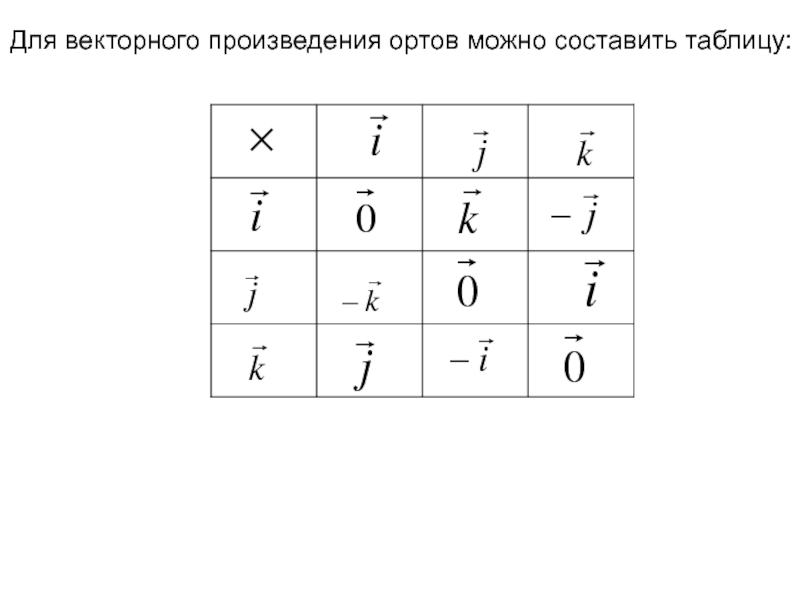
- 79. Для векторного произведения ортов можно составить таблицу:
- 80. Пусть векторы заданы своими координатами:
- 82. Полученную формулу можно представить в виде определителя:
- 83. Приложение векторного произведения к геометрии 1.
- 84. Пример. Найти площадь параллелограмма построенного на векторах
- 85. Решение: Таким образом, Значит
- 86. Пример. Найти вектор
- 87. Так, как то
- 88. §8. Смешанное произведение трёх векторов.
- 89. Свойства смешанного произведения. 1. Смешанное произведение не
- 90. 3. Смешанное произведение не меняется при перемене
- 91. Выражение смешанного произведения через координаты. Пусть заданы векторы Тогда
- 92. Некоторые приложения смешанного произведения. 1. Определение
- 93. 3. Определение объемов пространственных фигур. Объем
- 94. Объем треугольной пирамиды, построенной на векторах
- 95. Пример. Даны векторы
- 96. Пример. Найти объем треугольной пирамиды, вершинами которой
- 97. Тогда
Слайд 2§1. Векторы. Основные определения.
Величины, которые полностью определяются заданием их числовых значений
Величины, для определения которых, кроме числового значения, необходимо знать еще и направление (например, сила, скорость, ускорение и т.д.), называются векторными. Векторные величины геометрически изображаются с помощью векторов.
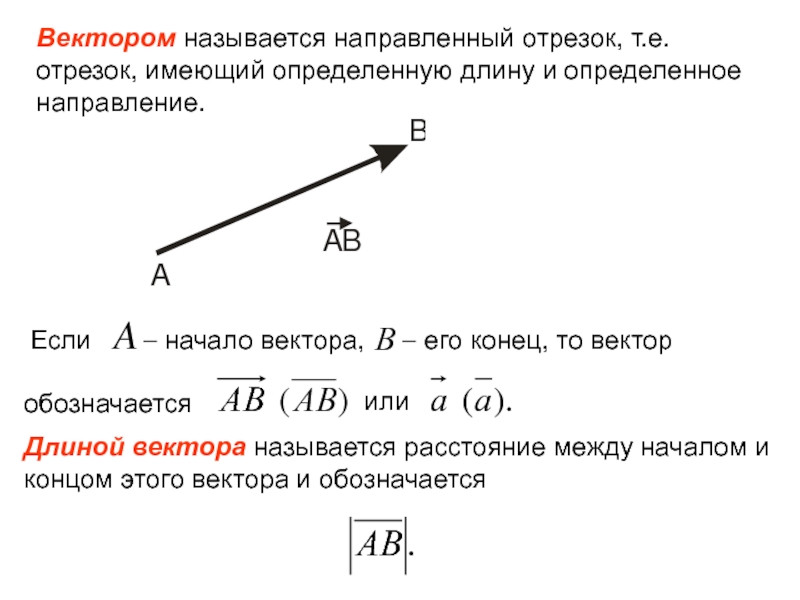
Слайд 3Вектором называется направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное
Если
− начало вектора,
− его конец, то вектор
обозначается
или
Длиной вектора называется расстояние между началом и концом этого вектора и обозначается
Слайд 4Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается
Слайд 5Векторы
и
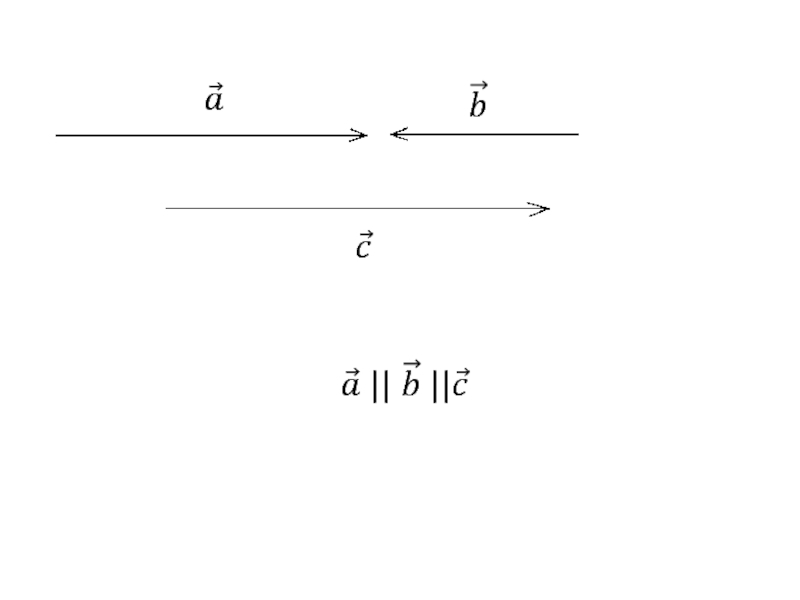
называются коллинеарными, если они
лежат либо на одной прямой,
записывают
||
Нулевой вектор считается коллинеарным любому вектору.
Слайд 7Два вектора называются равными, если они
а) коллинеарны,
б) одинаково направлены,
в)
Слайд 8Вектор можно переносить в любую точку пространства посредством параллельного переноса (это
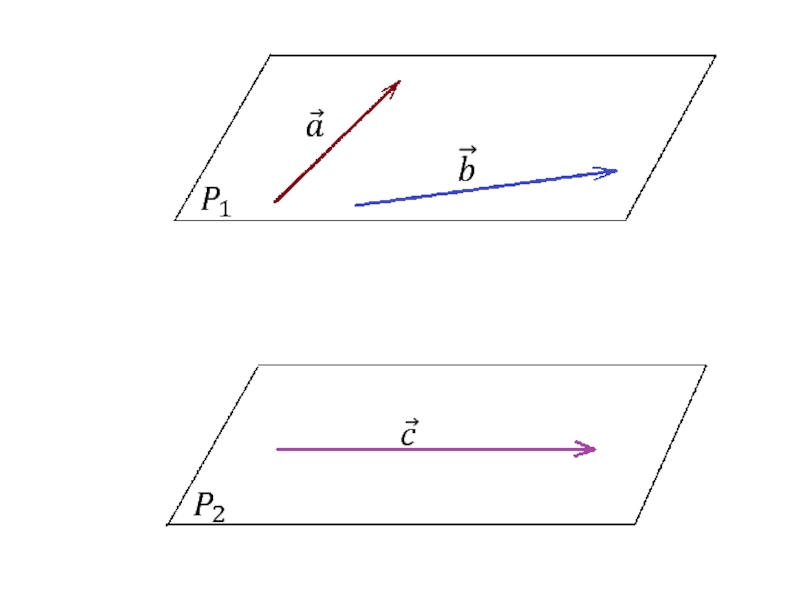
Векторы в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Слайд 10§2. Линейные операции над векторами.
Под линейными операциями над векторами понимают
а) произведение
б) сложение и вычитание векторов.
Произведением вектора
на число
называется вектор
удовлетворяющий следующим
условиям:
а) длина вектора
равна произведению модуля числа
на длину вектора
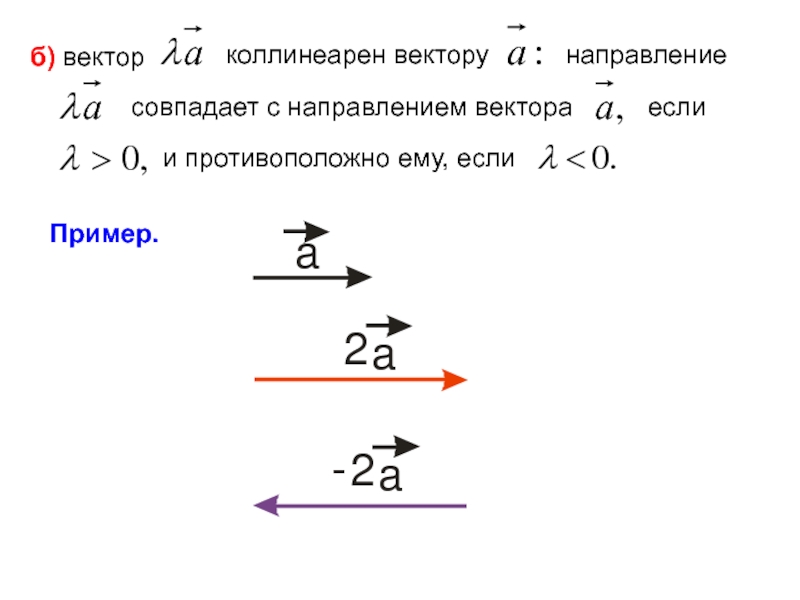
Слайд 11б) вектор
коллинеарен вектору
направление
совпадает с направлением
если
и противоположно ему, если
Пример.
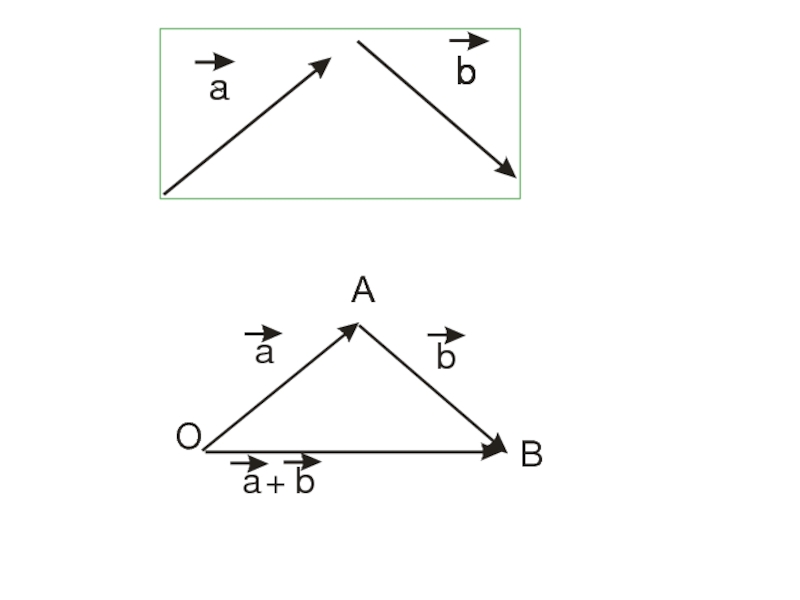
Слайд 12Сумму двух векторов можно находить либо по правилу треугольников, либо по
Правило треугольников.
Пусть
и
− два произвольных вектора. Возьмем
произвольную точку
и построим вектор
От точки
отложим вектор
Вектор
соединяющий начало первого вектора с концом второго,
называется суммой векторов
и
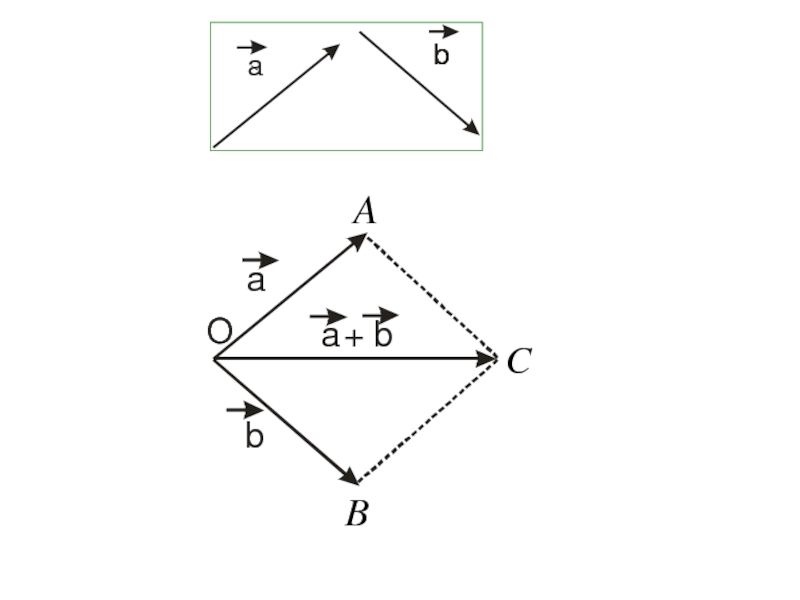
Слайд 14Правило параллелограмма.
Пусть
и
− два произвольных вектора. Возьмем
произвольную точку
и построим векторы
и
Суммой двух векторов
и
называется вектор
диагонали параллелограмма
построенного на векторах
и
Слайд 16Сумму трех и более векторов можно находить по правилу замыкания ломаной:
Чтобы
нужно конец вектора
совместить с началом вектора
конец вектора
– с началом вектора
и т.д.,
пока не дойдем до вектора
Тогда суммой
будет вектор,
идущий из начала вектора
в конец вектора
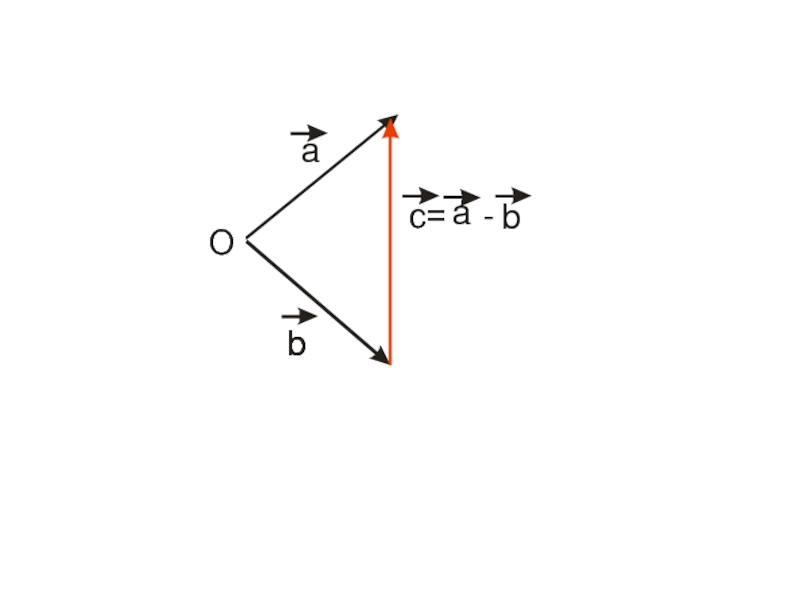
Слайд 17Разностью двух векторов
и
называется такой
вектор
который нужно сложить с
чтобы получить вектор
т.е.
Чтобы построить вектор
нужно
параллельным переносом перенести векторы
и
к общему началу, и тогда вектор
будет
выходить из конца вектора
в конец вектора
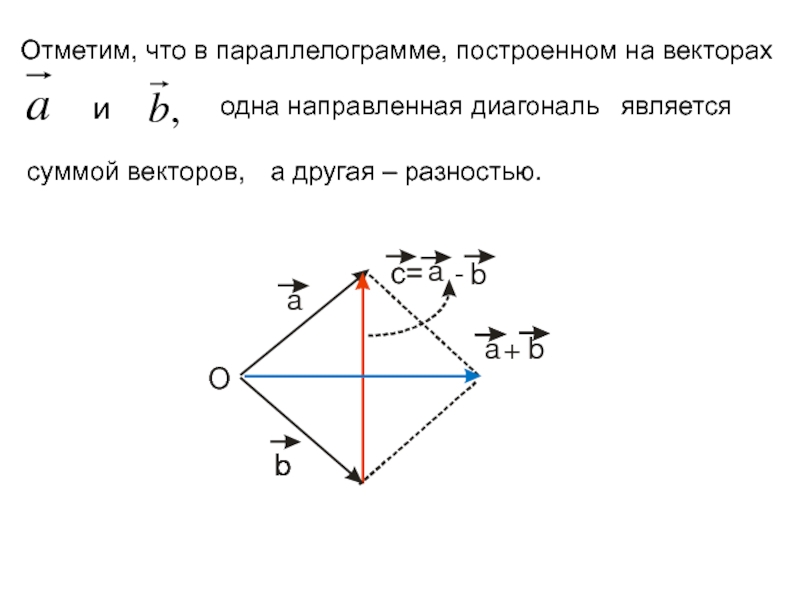
Слайд 19Отметим, что в параллелограмме, построенном на векторах
и
одна направленная
является
суммой векторов,
а другая – разностью.
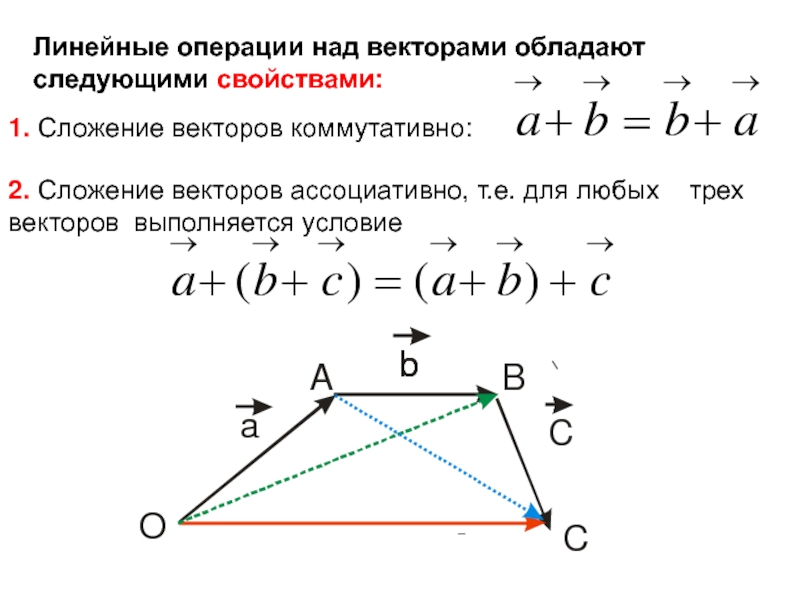
Слайд 20Линейные операции над векторами обладают следующими свойствами:
1. Сложение векторов коммутативно:
2.
Слайд 213. Прибавление нулевого вектора к любому вектору не меняет последнего:
4. Вектор
называется противоположным вектору
и обозначается
5. Умножение вектора на единицу не меняет этого вектора:
6. Умножение вектора на число ассоциативно, т.е.
Слайд 227. Умножение вектора на число дистрибутивно по отношению к сложению чисел,
8. Умножение вектора на число дистрибутивно по отношению к сложению векторов, т.е.
Эти свойства позволяют проводить преобразования в
линейных операциях над векторами так, как это делается в
обычной алгебре: слагаемые менять местами, вводить
скобки, группировать, выносить за скобки как скалярные,
так и векторные множители.
Слайд 23§3. Проекция вектора на ось.
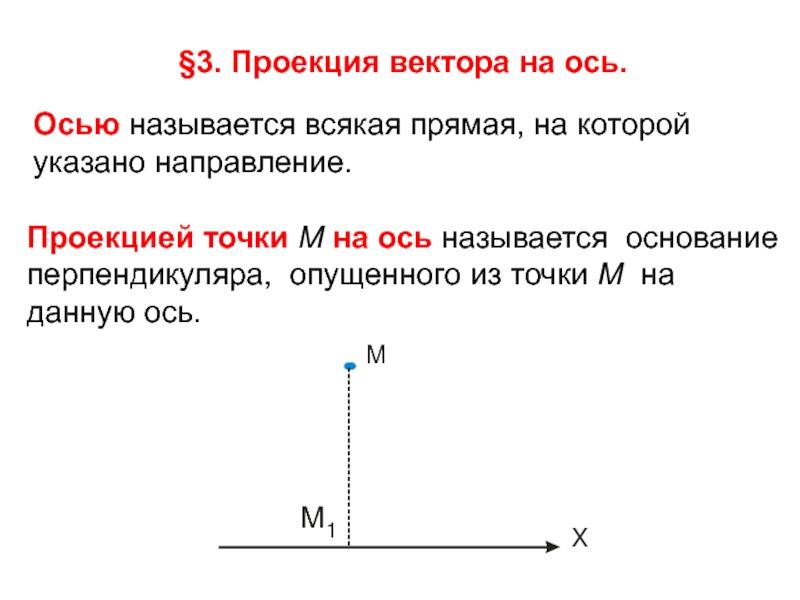
Осью называется всякая прямая, на которой
указано направление.
Проекцией точки М на ось называется основание перпендикуляра, опущенного из точки М на данную ось.
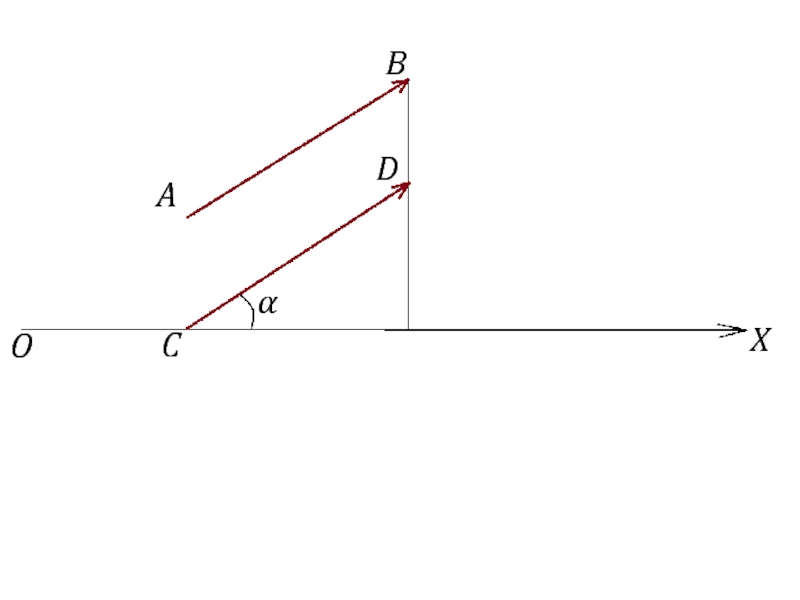
Слайд 24Углом между вектором
или равным ему вектором
и осью Ox называется
на который нужно
повернуть кратчайшим образом полуось Сx, до совмещения
ее с вектором
Область изменения угла
Слайд 26Проекцией вектора
на ось Ох называется число,
обозначаемое
и равное
где
– угол между вектором
и осью Ох, т.е.
по определению
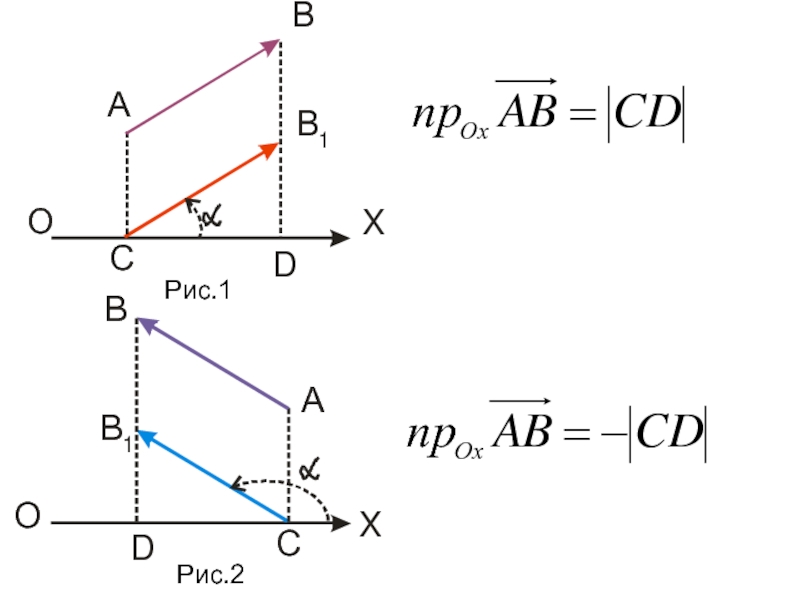
Слайд 27Геометрически проекция вектора
на ось Ох равна
длине отрезка СD,
(рис.1), и со знаком «–», если
При
отрезок CD превращается в точку и
(рис.2).
Слайд 291. При умножении вектора
на число m,
его проекция на ось
Свойства проекции вектора на ось.
2. Проекция суммы двух векторов на ось равна сумме
проекций составляющих на ту же ось:
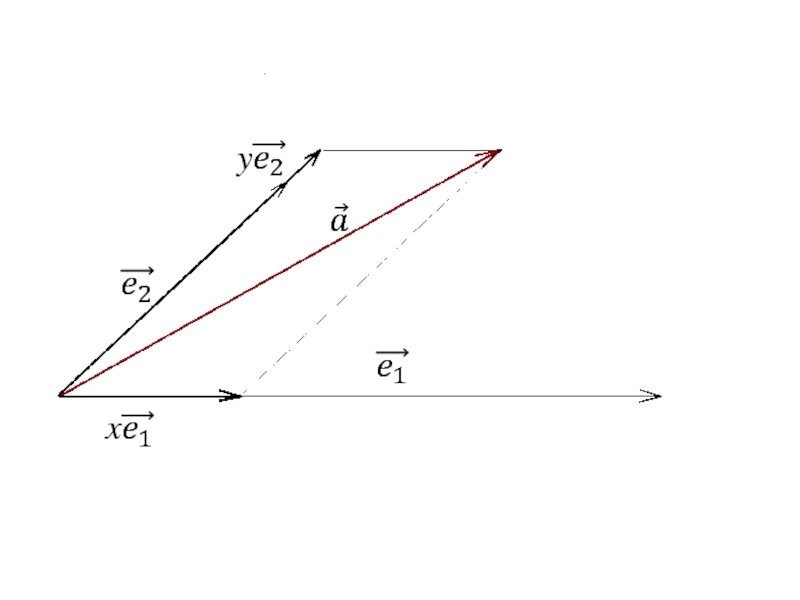
Слайд 30§4. Базис. Разложение вектора по базису. Координаты вектора. Декартова система координат.
Базисом
Теорема. Если на плоскости выбран базис
то любой вектор
этой плоскости можно разложить по
векторам
и такое разложение единственно:
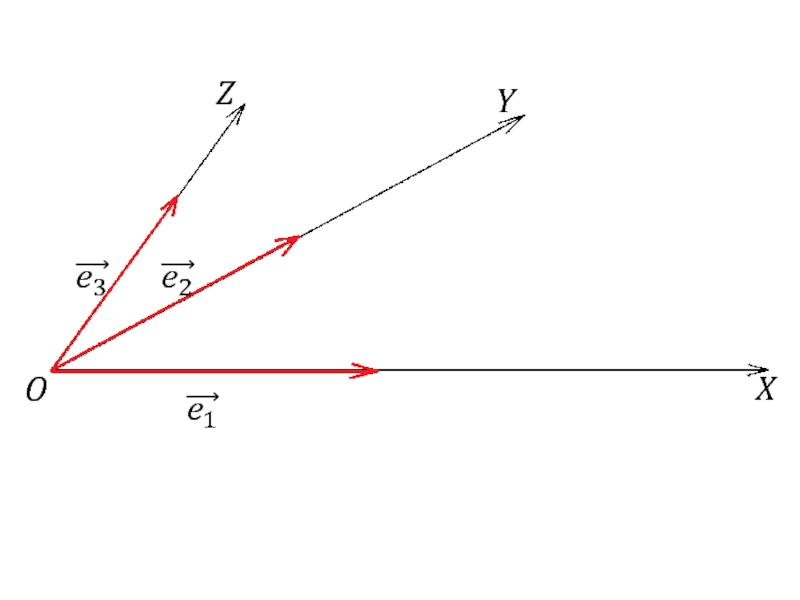
Слайд 32Базисом в пространстве называют любые три некомпланарных вектора в этом пространстве,
Теорема. Если в пространстве выбран базис
то любой вектор
этой плоскости можно разложить
по векторам
,
и такое разложение единственно:
Слайд 33При этом коэффициенты
в данном разложении
называют координатами вектора
в базисе
и записывают
или
.
Для векторов, заданных своими координатами, имеют место следующие свойства.
1. При умножении вектора
на число
все его координаты умножаются на это число:
Слайд 342. При сложении (вычитании) векторов
и
складываются (вычитаются) их
соответствующие
3. Вектор
коллинеарен вектору
т.е.
, если выполняется условие
или
где
− некоторое число.
Слайд 36
Декартовой системой координат в пространстве называют совокупность фиксированной точки
.
Точка О называется началом координат, а прямые, проходящие через начало координат в направлении базисных векторов − осями координат.
Слайд 38Прямая ОX называется осью абсцисс, прямая ОY − осью ординат, прямая
Вектор
для произвольной точки М называют ее
радиус-вектором.
Координаты радиуса-вектора точки М по отношению к началу координат называют координатами точки М в рассматриваемой системе координат. Первая координата называется абсциссой, вторая − ординатой, третья − аппликатой.
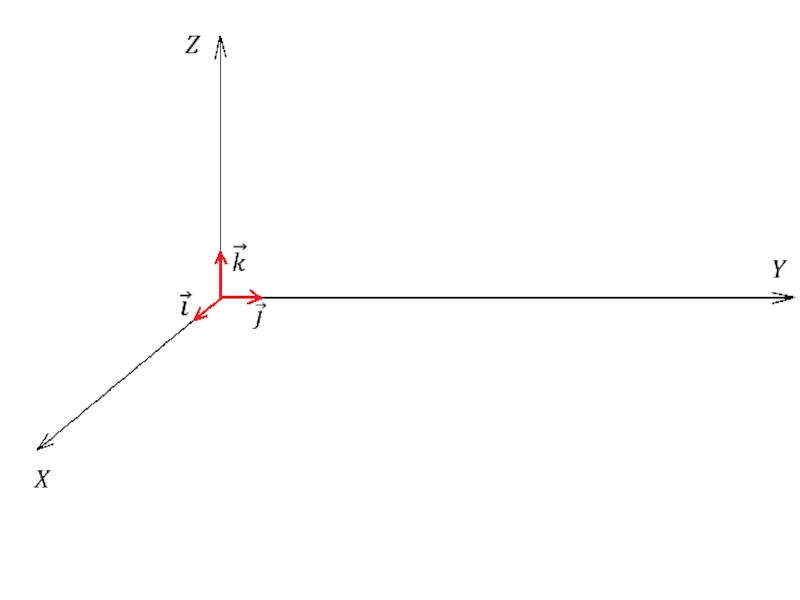
Слайд 39Базис называют ортонормированным, если базисные векторы попарно ортогональны и длина каждого
в пространстве −
Декартова система координат с ортонормированным базисом называется прямоугольной системой координат.
Слайд 43
Учитывая, что при вычитании векторов вычитаются их
соответствующие координаты, имеем
т.е. если заданы координаты начала и конца вектора, то чтобы найти координаты этого вектора, надо из соответствующей координаты его конца вычесть координату начала.
Слайд 44А длина вектора
определяется по формуле
Для точек
заданных на
последняя формула примет вид
В частности,
аналогично,
Слайд 45Отметим, что в прямоугольной системе координаты вектора
равны соответственно проекциям
оси координат:
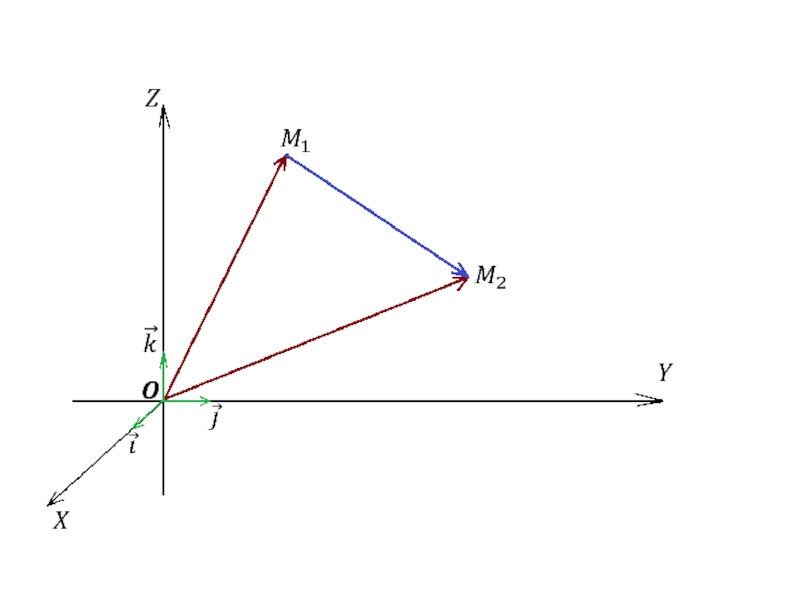
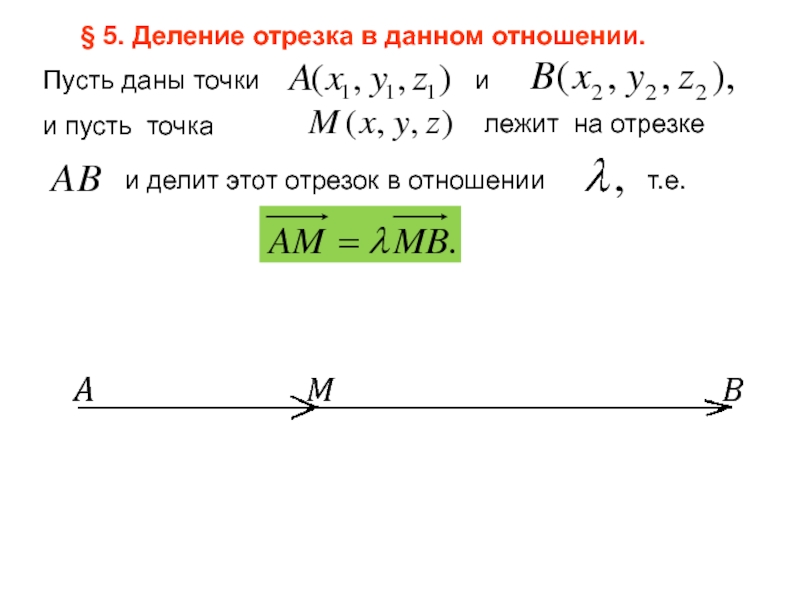
Слайд 47Пусть даны точки
и
и пусть точка
лежит на
и делит этот отрезок в отношении
т.е.
§ 5. Деление отрезка в данном отношении.
Слайд 49При
точка
делит отрезок
пополам и последние формулы
т.е. координаты середины отрезка равны полусумме
соответствующих координат его концов.
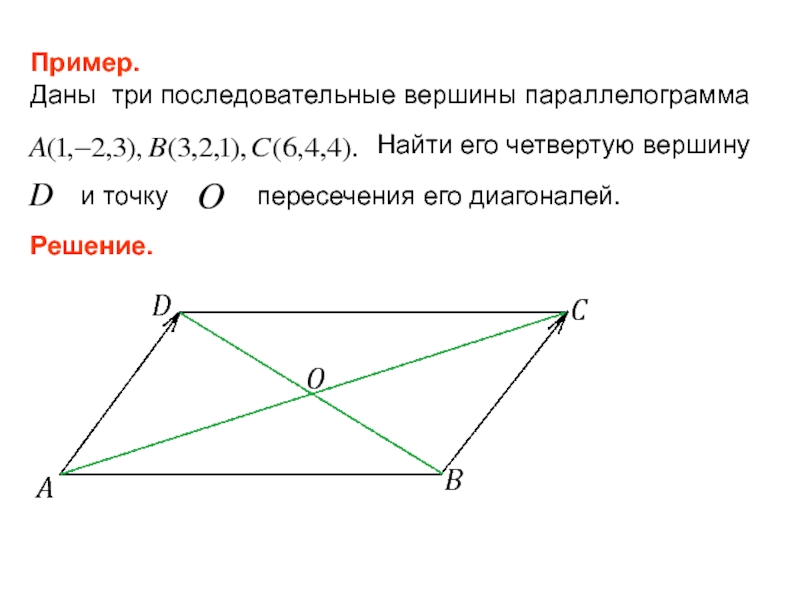
Слайд 50Пример.
Даны три последовательные вершины параллелограмма
Найти его четвертую вершину
и точку
пересечения его диагоналей.
Решение.
Слайд 53§6. Скалярное произведение векторов.
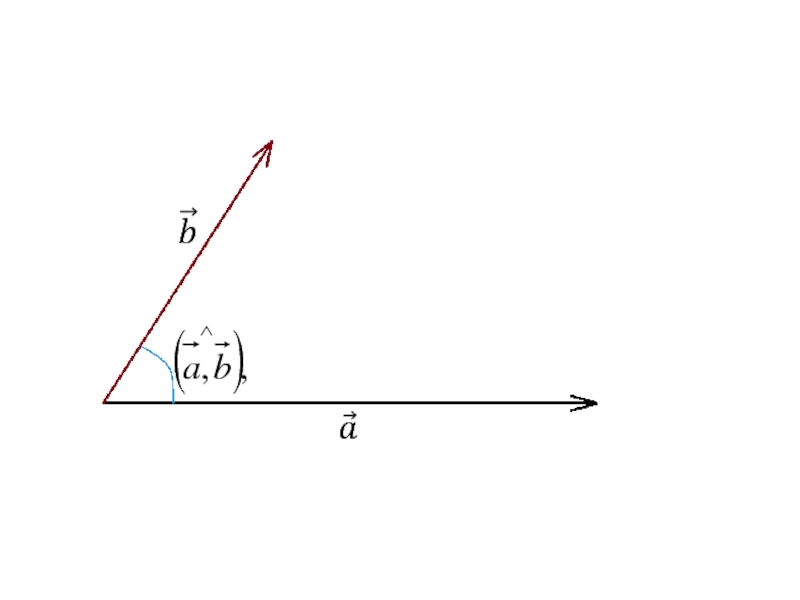
Углом между двумя векторами называется
наименьший
угол между этими
Угол между векторами
и
символически
записывают
причем
Слайд 55Скалярным произведением двух векторов называется
число, равное произведению длин этих векторов на
косинус угла между ними:
Скалярное произведение принято обозначать
или
или
Слайд 56Скалярное умножение обладает следующими свойствами.
1. Скалярное умножение коммутативно:
2. Для
модуля:
Из последнего равенства следует
Слайд 573. Скалярное произведение равно нулю, если сомножители
ортогональны или хотя бы
⊥
или
или
4. Скалярное умножение обладает свойством
ассоциативности относительно скалярного множителя:
5. Скалярное умножение дистрибутивно относительно
сложения:
Слайд 60Пример 3. Вычислить скалярное произведение
если
где
−
единичные
векторы, а угол между ними равен
Решение.
Слайд 61Пусть в прямоугольной системе координат векторы заданы
своими координатами:
и
Тогда скалярное произведение можно вычислять по формуле:
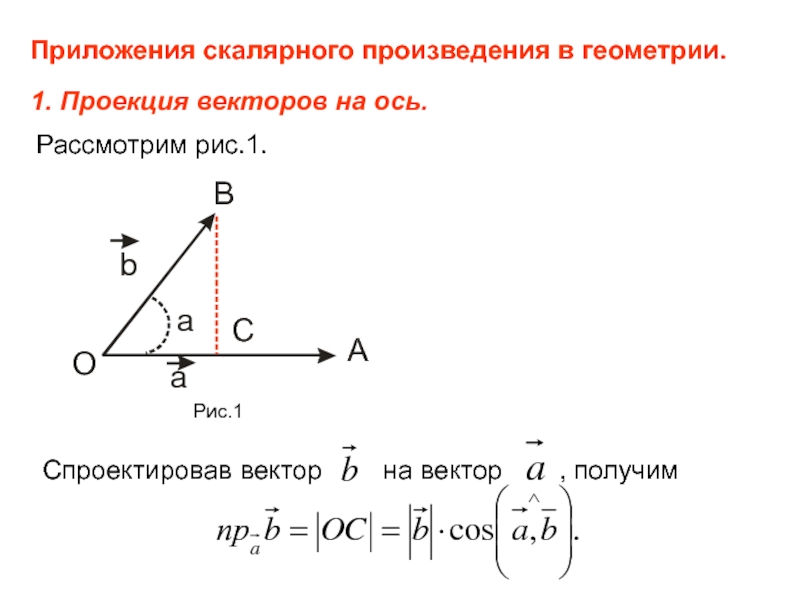
Слайд 62Приложения скалярного произведения в геометрии.
1. Проекция векторов на ось.
Рассмотрим рис.1.
Спроектировав вектор
на вектор
, получим
Слайд 63Поэтому
или
Таким образом, скалярное произведение двух векторов равно
модулю одного
вектора на первый.
Слайд 642. Угол между векторами.
Из определения скалярного произведения следует, что
Если
ортонормированном базисе:
и
то последнюю формулу можно переписать так:
Слайд 653. Направляющие косинусы векторов.
Направление вектора
определяется углами
образованными
с положительными направлениями осей
соответственно
(или вектором
с векторами
соответственно). Косинусы этих углов называются
направляющими косинусами этого вектора.
Найдем их.
Слайд 67Косинусы углов, образованных вектором и осями координат Ox, Oy, Oz, называются
Слайд 68Пример. Даны вершины треугольника
Вычислить внутренний угол при вершине
Решение. Внутренний угол при вершине А − это угол
между векторами
и
Так как
то
Следовательно,
Слайд 69Пример. Вычислить угол между вектором
и осью
Решение. Угол между
и осью
− это
угол между вектором
и вектором
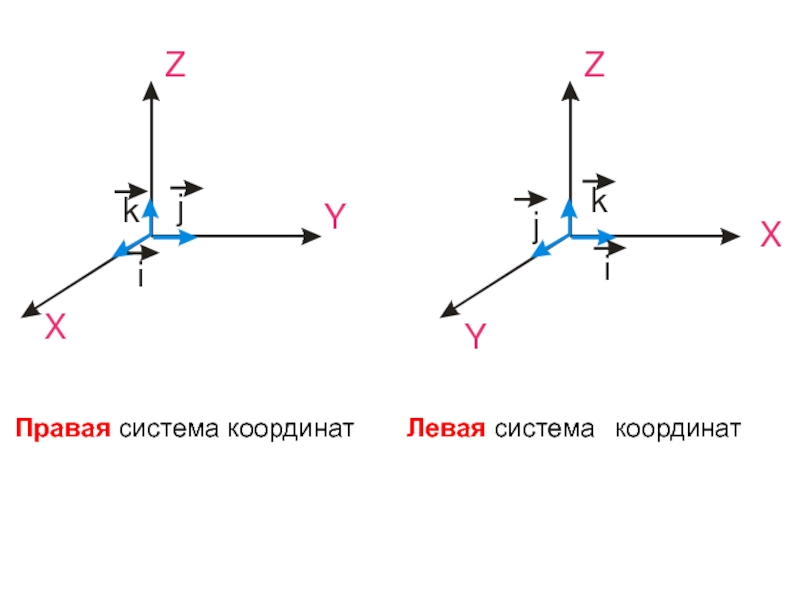
Слайд 71§7. Векторное произведение векторов.
Упорядоченная тройка некомпланарных векторов
называется правой, если
кратчайший поворот от первого вектора
ко второму
вектору
виден против хода часовой стрелки.
В противном случае тройка
называется левой.
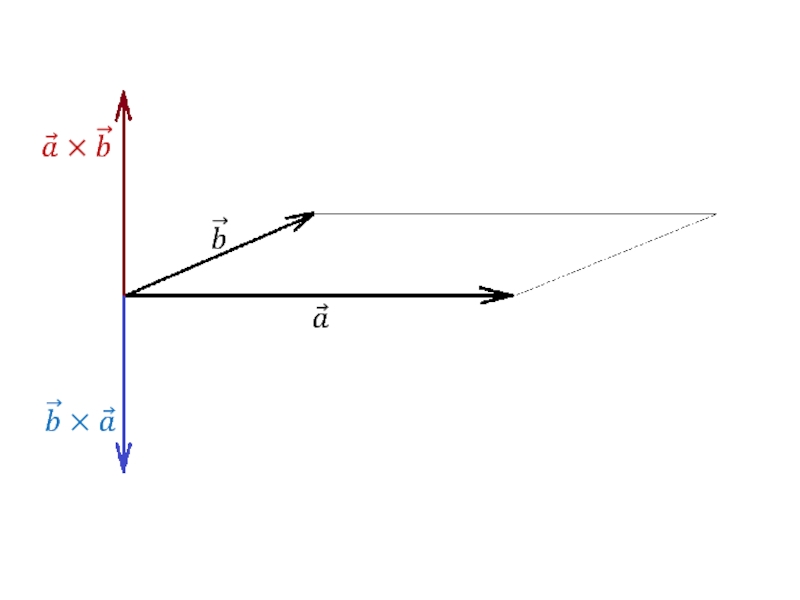
Слайд 73Векторным произведением векторов
и
называется вектор, обозначаемый
и удовлетворяющий
1)
2)
⊥
⊥
3) упорядоченная тройка
−
правая.
Важно:
Результатом векторного произведения является вектор.
Слайд 75Свойства векторного произведения:
1) От перестановки множителей векторное произведение меняет направление на
2) Если в векторном произведении изменить знак одного из сомножителей на противоположный, то векторное произведение изменит знак, т.е.
3) Скалярный множитель можно выносить за знак векторного произведения.
Слайд 764)
5) Векторное произведение равно нулю, если хотя бы один из
или
или
6)
Слайд 78
Параллелограмм, построенный на
площадь которого равна единице.
перпендикулярен векторам
и образует
есть квадрат ОАDB,
Вектор
есть единичный вектор, направленный по оси OZ, т.е.
Аналогично находим, что
Переставив множители, получим
Слайд 83
Приложение векторного произведения к геометрии
1. Площадь параллелограмма построенного на векторах
равна
2. Площадь треугольника построенного на векторах
равна
половине модуля векторного произведения:
Слайд 86Пример. Найти вектор
если известно, что он
перпендикулярен к векторам
и удовлетворяет условию
где
Решение. Так, как вектор
перпендикулярен к
плоскости векторов
и
а вектор
также перпендикулярен к плоскости этих векторов по
определению, то отсюда следует, что
Имеем
Слайд 88
§8. Смешанное произведение трёх векторов.
Смешанным произведением векторов
называется число, обозначаемое
и определяемое
как скалярное произведение вектора
и вектора
Результатом смешанного произведения является число.
Слайд 89Свойства смешанного произведения.
1. Смешанное произведение не меняется при циклической
перестановке трех его
2. Смешанное произведение меняет знак на
противоположный при перестановке любых двух
векторов-сомножителей:
Слайд 903. Смешанное произведение не меняется при перемене
местами знаков векторного и
4. Смешанное произведение ненулевых векторов равно
нулю тогда и только тогда, когда векторы компланарны:
и
− компланарны.
Слайд 92Некоторые приложения смешанного произведения.
1. Определение взаимной ориентации векторов в
пространстве.
Если
то
− правая тройка;
если же
то
− левая тройка.
2. Установление компланарности векторов.
Векторы
− компланарны ⇔
Слайд 933. Определение объемов пространственных фигур.
Объем параллелепипеда, построенного на векторах
и
вычисляется по формуле:
Объем треугольной призмы, построенной на векторах
и
вычисляется по формуле:
Слайд 95Пример. Даны векторы
Выяснить ориентацию тройки векторов
Решение.
Составим и
− левая тройка векторов.