СОШ 256
г.Фокино.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная и ее применение. презентация
Содержание
- 1. Производная и ее применение.
- 2. «Если продолжить одно из маленьких звеньев ломаной,
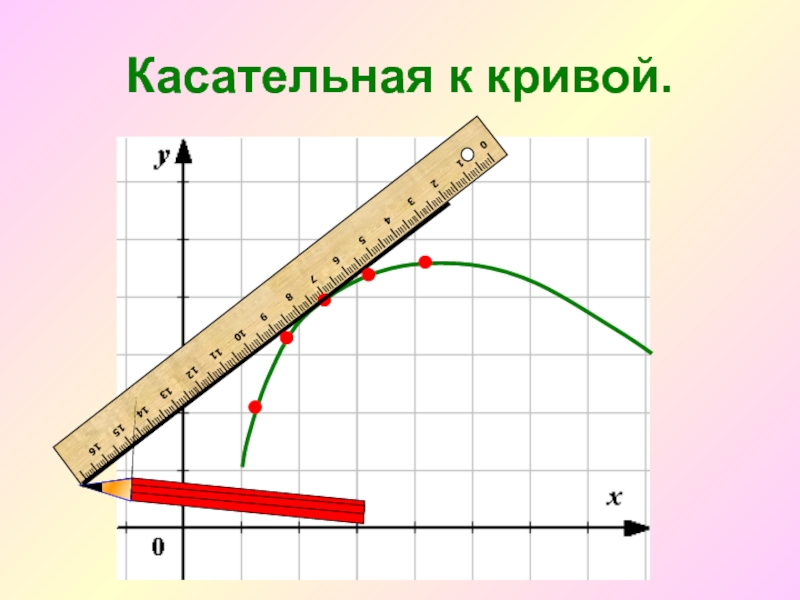
- 3. Касательная к кривой.
- 4. Производная - это угловой коэффициент касательной. Р Р1
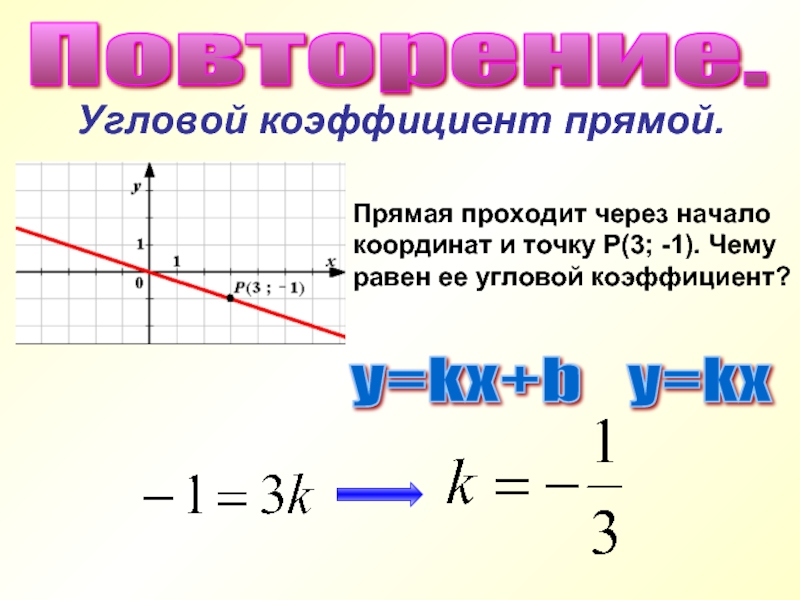
- 5. Угловой коэффициент прямой. Прямая проходит через начало
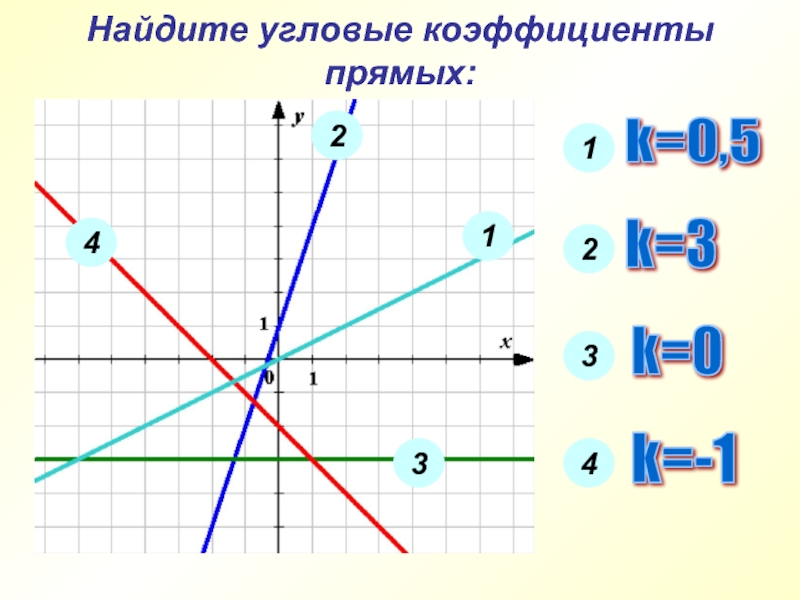
- 6. Найдите угловые коэффициенты прямых: 2 1 3
- 12. Исаак Ньютон (1643 – 1727) «Когда
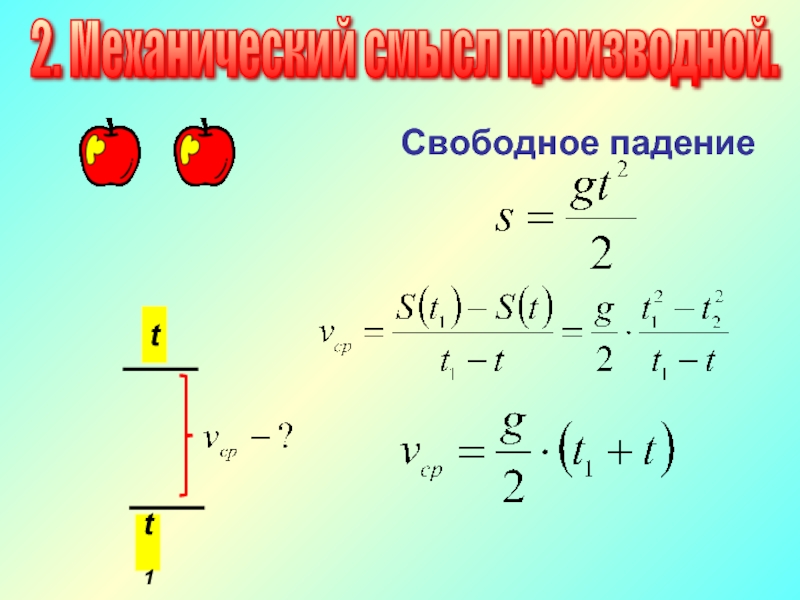
- 13. 2. Механический смысл производной. t t1 Свободное падение
- 14. 2. Механический смысл производной. t t1 Свободное
- 15. Используя слово «предел», можно сказать,
- 16. . Δх
Слайд 1Производная
и ее применение.
2. Механический смысл производной.
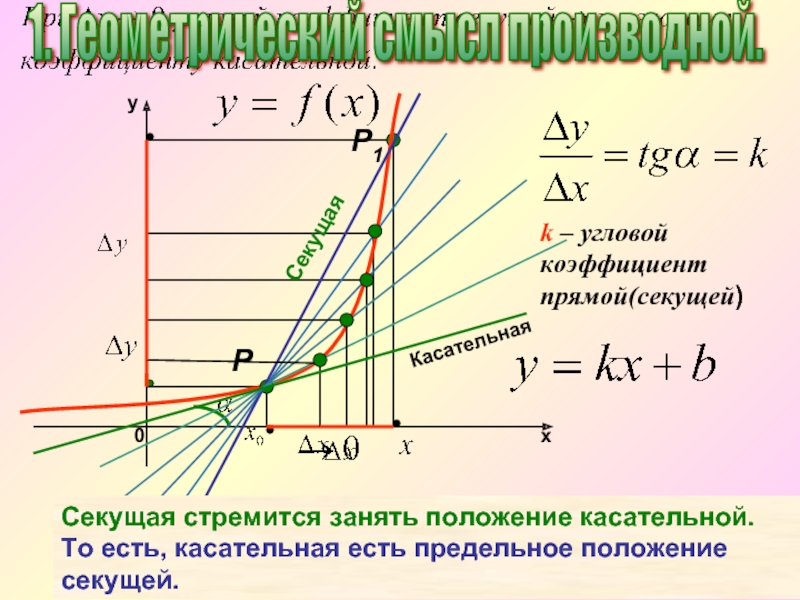
1. Геометрический смысл производной.
11 класс.
МОУ
Слайд 2«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то
эта продолженная таким образом сторона будет называться касательной к кривой.»
1. Геометрический смысл производной.
Слайд 5Угловой коэффициент прямой.
Прямая проходит через начало
координат и точку Р(3; -1).
Чему
равен ее угловой коэффициент?
равен ее угловой коэффициент?
y=kx+b
y=kx
Повторение.
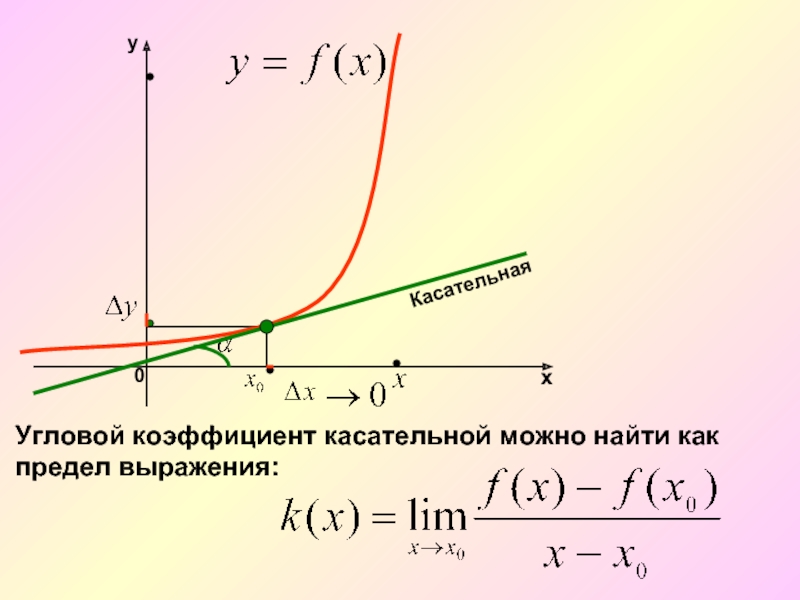
Слайд 7
k – угловой
коэффициент прямой(секущей)
Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.
Секущая
1. Геометрический смысл производной.
Р
Р1
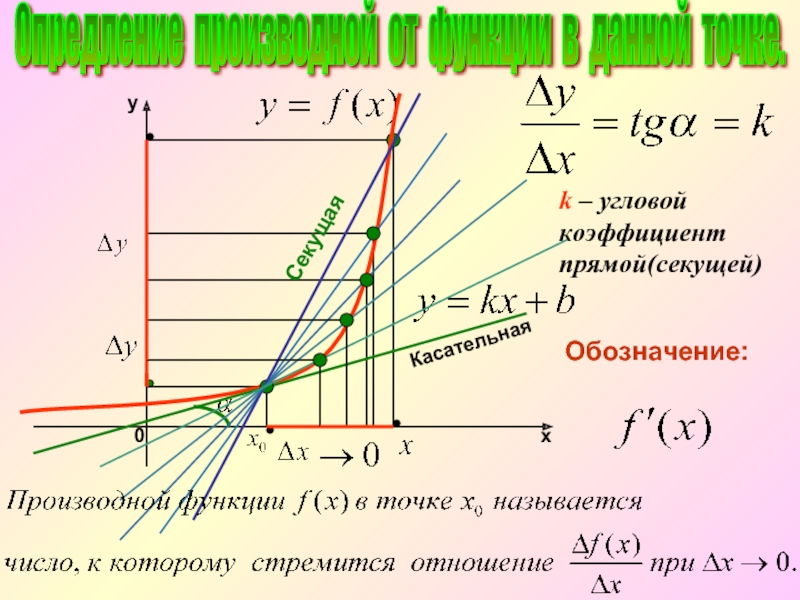
Слайд 9
k – угловой коэффициент прямой(секущей)
Касательная
Секущая
Опредление производной
от функции в данной точке.
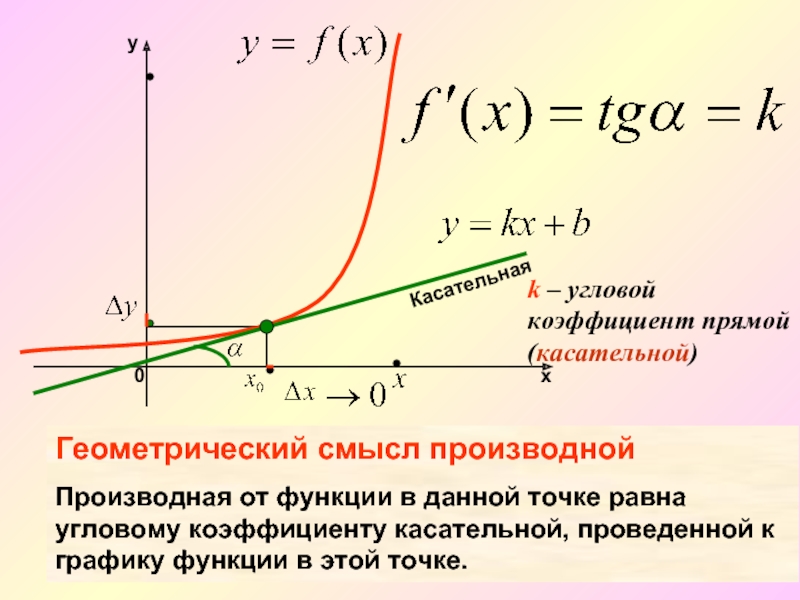
Слайд 10
k – угловой
коэффициент прямой(касательной)
Касательная
Геометрический смысл производной
Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
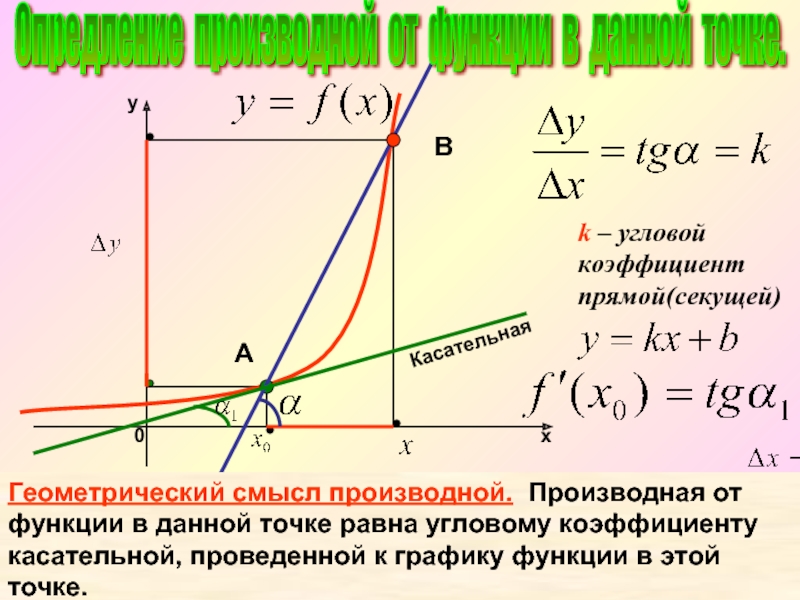
Слайд 11
k – угловой коэффициент прямой(секущей)
Касательная
А
В
Геометрический смысл
производной. Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Опредление производной от функции в данной точке.
Слайд 12Исаак Ньютон (1643 – 1727)
«Когда величина является максимальной или минимальной,
в этот момент она не течет ни вперед, ни назад.»
2. Механический смысл производной.
Слайд 15 Используя слово «предел», можно сказать, что мгновенная скорость в
точке t – это предел средней скорости при стягивании отрезка, на котором она изменяется, в точку t или в символической записи
2. Механический смысл производной.
Производная
- это скорость
Слайд 16
.
Δх – перемещение тела
Δt – промежуток времени
в течение которого выполнялось
движение
2. Механический
смысл производной.
