- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построения сечений при наличии трёх данных точек. Виды сечений. презентация
Содержание
Слайд 1Сечения куба плоскостью
Построения сечений при наличии трёх данных точек.
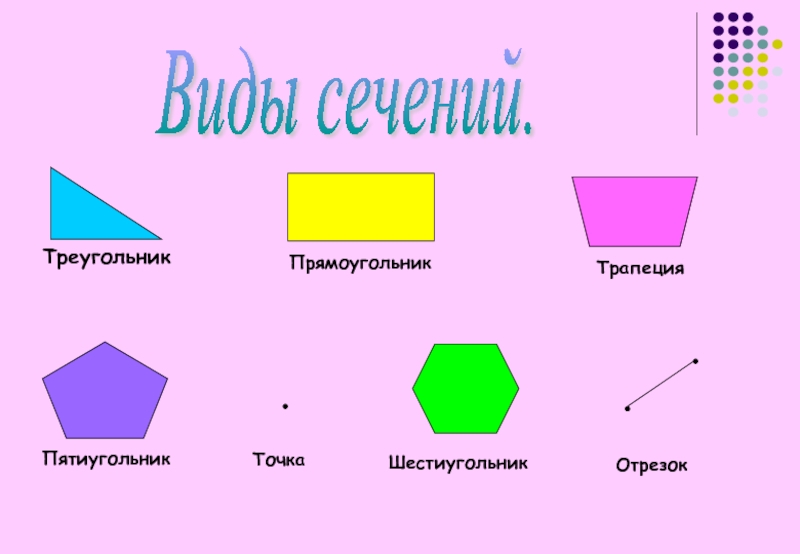
Виды сечений.
Выполнила
Цывунина
Ученица 10 «Г» класса
Преподаватель
Соловьева А.Х.
Слайд 2Задача № 1.
М
Р
К
А
А1
В
В1
D
D1
С
С1
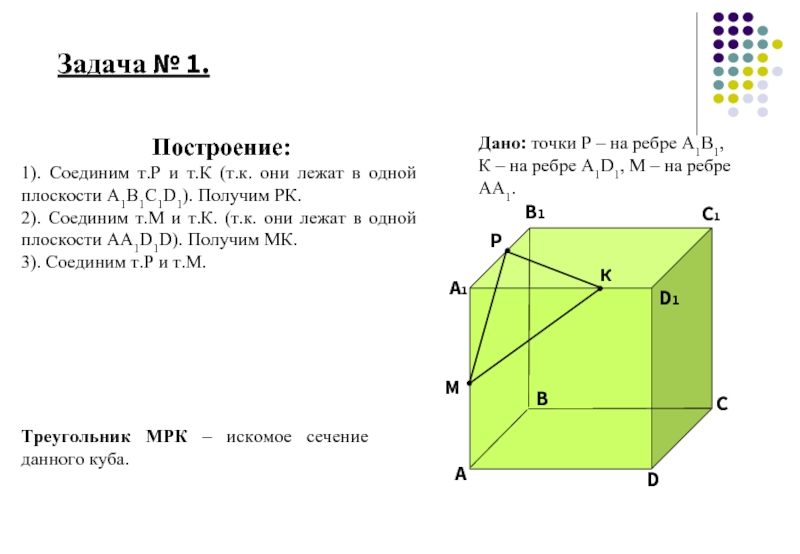
Построение:
1). Соединим т.Р и т.К (т.к. они
2). Соединим т.М и т.К. (т.к. они лежат в одной плоскости АА1D1D). Получим МК.
3). Соединим т.Р и т.М.
Треугольник МРК – искомое сечение данного куба.
Дано: точки P – на ребре А1В1, К – на ребре А1D1, М – на ребре АА1.
Слайд 3Задача № 2.
А
А1
В
В1
D
D1
С
С1
Р
М
К
N
T
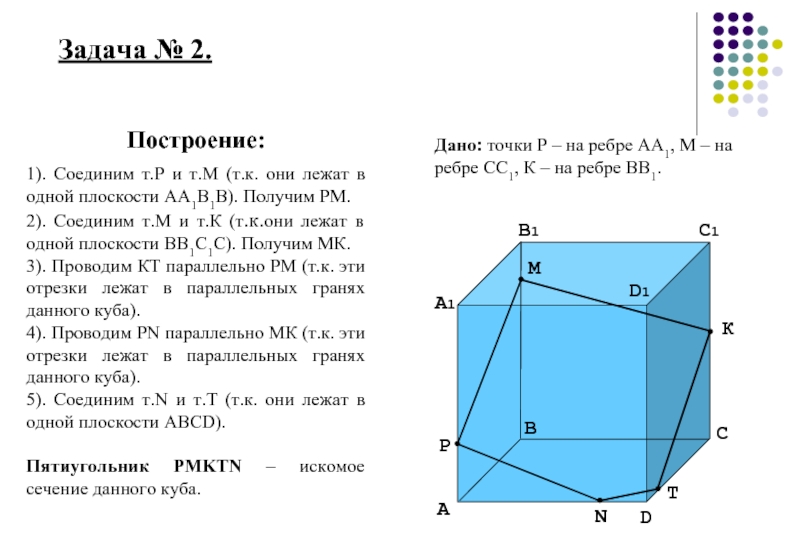
Построение:
1). Соединим т.Р и т.М (т.к. они лежат в
2). Соединим т.М и т.К (т.к.они лежат в одной плоскости ВВ1С1С). Получим МК.
3). Проводим КТ параллельно РМ (т.к. эти отрезки лежат в параллельных гранях данного куба).
4). Проводим PN параллельно МК (т.к. эти отрезки лежат в параллельных гранях данного куба).
5). Соединим т.N и т.Т (т.к. они лежат в одной плоскости АВСD).
Пятиугольник PMKTN – искомое сечение данного куба.
Дано: точки Р – на ребре АА1, М – на ребре СС1, К – на ребре ВВ1.
Слайд 4Задача № 3.
A
A1
B
B1
C
C1
D
D1
M
F
E
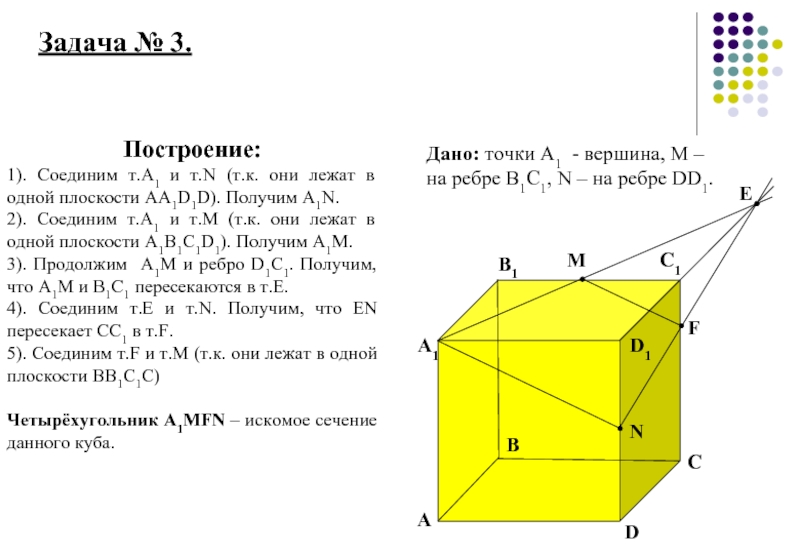
Дано: точки А1 - вершина, М – на ребре
Построение:
1). Соединим т.А1 и т.N (т.к. они лежат в одной плоскости АА1D1D). Получим А1N.
2). Соединим т.А1 и т.М (т.к. они лежат в одной плоскости А1В1С1D1). Получим А1М.
3). Продолжим А1М и ребро D1C1. Получим, что А1М и В1С1 пересекаются в т.Е.
4). Соединим т.Е и т.N. Получим, что ЕN пересекает СС1 в т.F.
5). Соединим т.F и т.M (т.к. они лежат в одной плоскости ВВ1С1С)
Четырёхугольник А1МFN – искомое сечение данного куба.
N
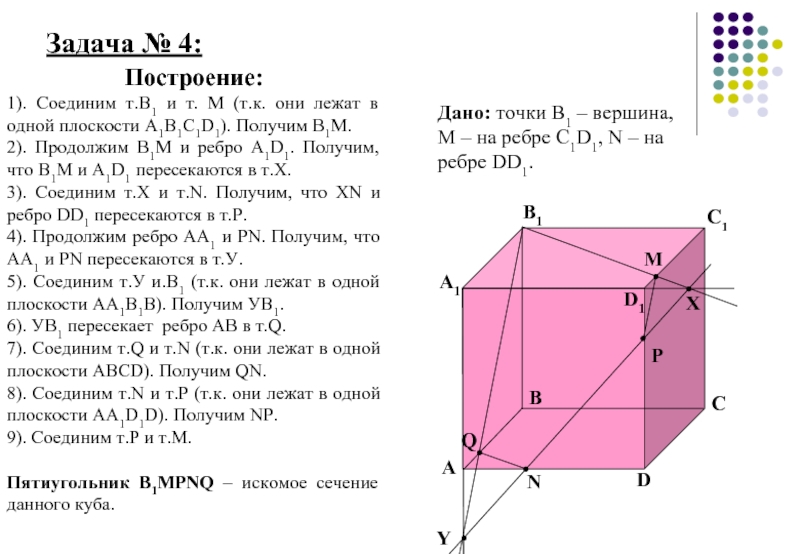
Слайд 5 Задача № 4:
А
А1
В1
В
С1
С
D1
D
Построение:
1). Соединим т.В1 и т. М (т.к. они
2). Продолжим В1М и ребро А1D1. Получим, что В1М и А1D1 пересекаются в т.Х.
3). Соединим т.Х и т.N. Получим, что XN и ребро DD1 пересекаются в т.Р.
4). Продолжим ребро AA1 и РN. Получим, что АА1 и РN пересекаются в т.У.
5). Соединим т.У и.В1 (т.к. они лежат в одной плоскости АА1В1В). Получим УВ1.
6). УВ1 пересекает ребро АВ в т.Q.
7). Соединим т.Q и т.N (т.к. они лежат в одной плоскости ABCD). Получим QN.
8). Соединим т.N и т.P (т.к. они лежат в одной плоскости АА1D1D). Получим NP.
9). Соединим т.Р и т.М.
Пятиугольник В1МРNQ – искомое сечение данного куба.
Дано: точки В1 – вершина, М – на ребре С1D1, N – на ребре DD1.
Q
N
Y
M
X
P
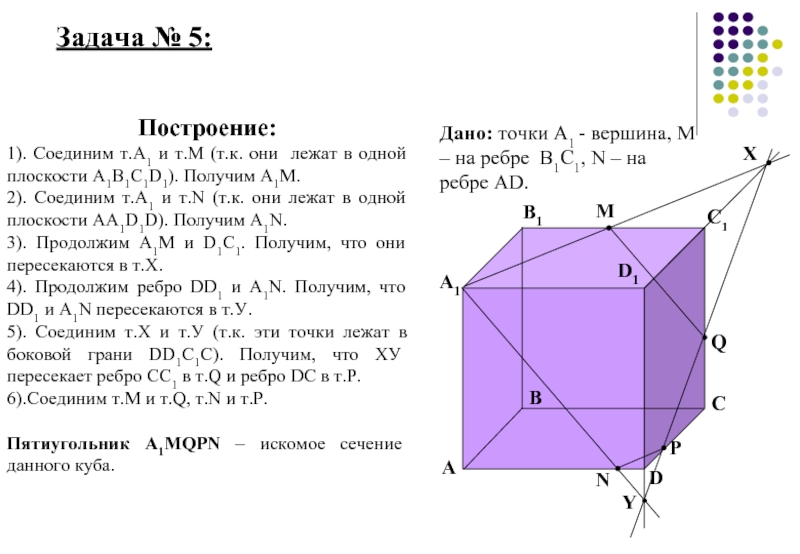
Слайд 6 Задача № 5:
А
А1
В1
В
С1
С
D1
D
Построение:
1). Соединим т.А1 и т.М (т.к. они лежат
2). Соединим т.А1 и т.N (т.к. они лежат в одной плоскости АА1D1D). Получим A1N.
3). Продолжим А1М и D1C1. Получим, что они пересекаются в т.Х.
4). Продолжим ребро DD1 и А1N. Получим, что DD1 и А1N пересекаются в т.У.
5). Соединим т.Х и т.У (т.к. эти точки лежат в боковой грани DD1C1C). Получим, что ХУ пересекает ребро СС1 в т.Q и ребро DC в т.Р.
6).Соединим т.М и т.Q, т.N и т.P.
Пятиугольник А1МQPN – искомое сечение данного куба.
Х
Q
P
Y
Дано: точки А1 - вершина, М – на ребре В1С1, N – на ребре AD.
N
M
Слайд 7
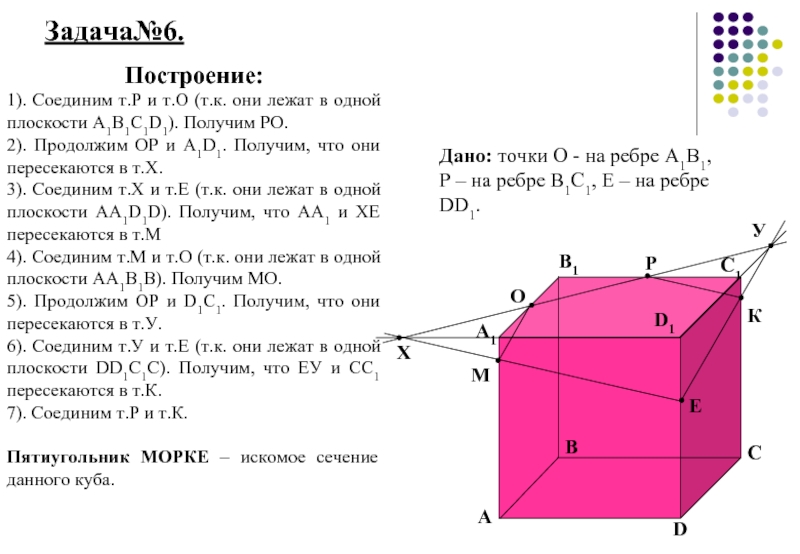
Задача№6.
А
А1
В1
В
С1
С
D1
D
Построение:
1). Соединим т.Р и т.О (т.к. они лежат в одной плоскости
2). Продолжим ОР и А1D1. Получим, что они пересекаются в т.Х.
3). Соединим т.Х и т.Е (т.к. они лежат в одной плоскости АА1D1D). Получим, что АА1 и ХЕ пересекаются в т.М
4). Соединим т.М и т.О (т.к. они лежат в одной плоскости АА1В1В). Получим МО.
5). Продолжим ОР и D1C1. Получим, что они пересекаются в т.У.
6). Соединим т.У и т.Е (т.к. они лежат в одной плоскости DD1C1C). Получим, что ЕУ и СС1 пересекаются в т.К.
7). Соединим т.Р и т.К.
Пятиугольник МОРКЕ – искомое сечение данного куба.
М
Р
О
К
Х
У
Е
Дано: точки О - на ребре А1В1, Р – на ребре В1С1, Е – на ребре DD1.