- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классическая теория конкуренции Лотки-Вольтерры: уравнения презентация
Содержание
- 1. Классическая теория конкуренции Лотки-Вольтерры: уравнения
- 2. Классическая теория конкуренции: нулевые изоклины 1 2
- 3. Классическая теория конкуренции: нулевые изоклины 1 2
- 4. Классическая модель конкуренции Вольтерры-Лотки Устойчивое сосуществование
- 5. Классическая теория конкуренции: была ли когда-нибудь предпринята
- 6. «Нам остается теперь рассмотреть второй этап конкуренции,
- 7. Ресурсная теория конкуренции Тильмана (David Tilman) (resource-based
- 8. Что такое пороговая концентрация ресурса R*? Удельная
- 9. Как определяется пороговая концентрация ресурса? Расчет пороговой
- 10. Механизм победы в конкуренции, основанный на пороговой
- 11. В хемостате оба конкурирующих вида испытывают одинаковый
- 12. Удельная скорость роста численности диатомовых водорослей Asterionella
- 13. Динамика численности Asterionella formosa (Af) и Synedra
- 14. Конкурентное вытеснение астерионеллы (Af) синедрой (Su) независимо
- 15. R1 Изоклины нулевого роста
- 16. N*c1 Вектор потребления C – это вектор,
- 17. Один потребитель и два ресурса Когда система
- 18. Как найти положение равновесия одного потребителя на
- 19. Конкуренция двух видов (A и B) за
- 20. Конкуренция двух видов (A и B) за
- 21. Как определить, является ли равновесие устойчивым? При
- 22. Конкуренция двух видов за два ресурса –
- 23. Конкуренция двух видов за два ресурса –
- 24. Конкуренция двух видов за два ресурса –
- 25. Rothhaupt 1988 (figure from Arthur 1988) Конкуренция
- 26. Из Rothhaupt 1988 Конкуренция двух видов за два ресурса – проверка теории
- 27. Сосуществование многих видов на ограниченном числе ресурсов
- 28. S – максимальная концентрация ресурса в данном
Слайд 1Классическая теория конкуренции Лотки-Вольтерры:
уравнения
Теория конкуренции подразумевает общий ресурс,
но ресурса в этих
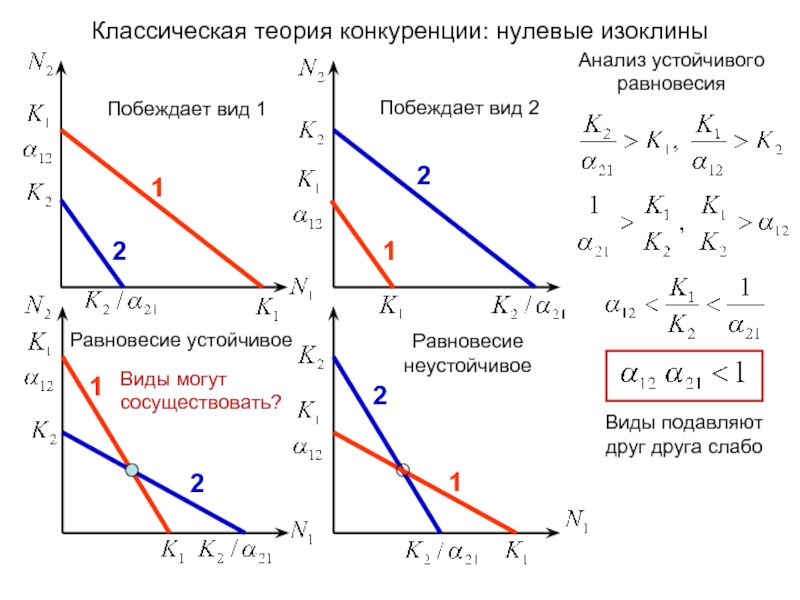
Слайд 2Классическая теория конкуренции: нулевые изоклины
1
2
Побеждает вид 1
2
Побеждает вид 2
1
2
Равновесие устойчивое
1
2
Равновесие неустойчивое
Анализ
Виды могут сосуществовать?
1
Виды подавляют друг друга сильно
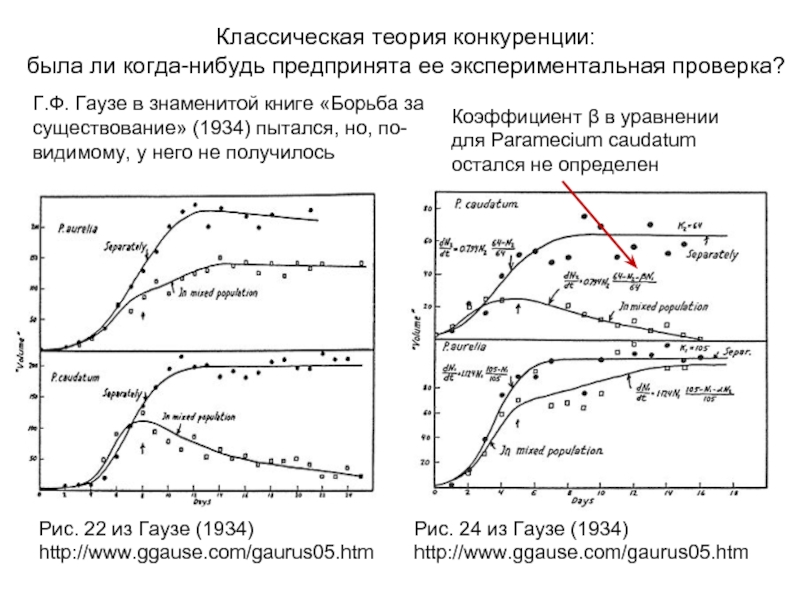
Слайд 3Классическая теория конкуренции: нулевые изоклины
1
2
Побеждает вид 1
2
Побеждает вид 2
1
2
Равновесие устойчивое
1
2
Равновесие неустойчивое
Анализ
Виды могут сосуществовать?
1
Виды подавляют друг друга слабо
Слайд 4Классическая модель конкуренции Вольтерры-Лотки
Устойчивое сосуществование
Виды подавляют друг друга слабо
Неустойчивое сосуществование
Виды подавляют
Принцип конкурентного исключения?
Слайд 5Классическая теория конкуренции:
была ли когда-нибудь предпринята ее экспериментальная проверка?
Г.Ф. Гаузе в
Рис. 24 из Гаузе (1934)
http://www.ggause.com/gaurus05.htm
Коэффициент β в уравнении для Paramecium caudatum остался не определен
Рис. 22 из Гаузе (1934)
http://www.ggause.com/gaurus05.htm
Слайд 6«Нам остается теперь рассмотреть второй этап конкуренции, т.е. непосредственное вытеснение одного
Слайд 7Ресурсная теория конкуренции Тильмана (David Tilman)
(resource-based competition theory)
(1) В теории в
(2) Успех вида в конкуренции определяется пороговой концентрацией ресурса для этого вида, а возможность сосуществования с др. видами – скоростью потребления лимитирующего ресурса (наклоном вектора потребления в точке равновесия)
(3) Это – графическая теория. Графическая теория не заменяет строгой математической теории. Однако теория, изложенная на графическом языке, часто (хотя не всегда!) обладает большей общностью и всегда обладает большей наглядностью, что облегчает ее восприятие и открывает возможность для экспериментальной проверки
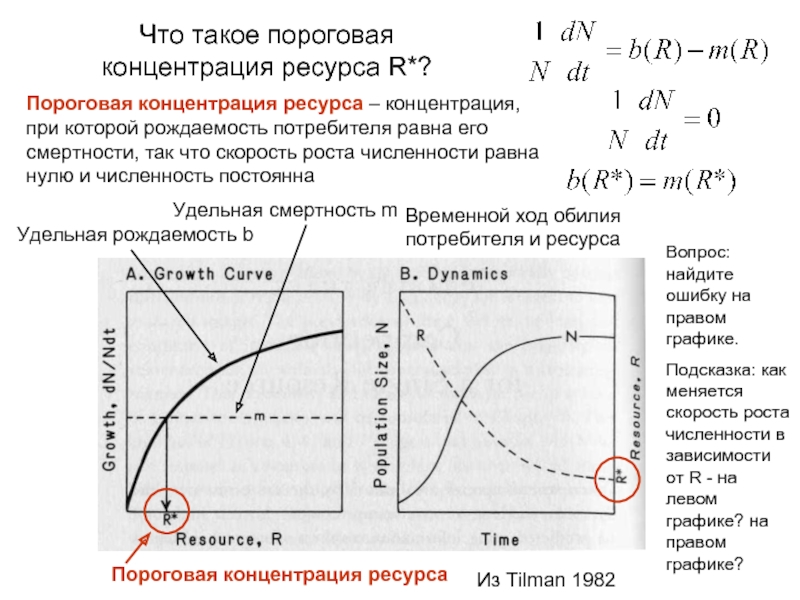
Слайд 8Что такое пороговая концентрация ресурса R*?
Удельная рождаемость b
Временной ход обилия потребителя
Пороговая концентрация ресурса – концентрация, при которой рождаемость потребителя равна его смертности, так что скорость роста численности равна нулю и численность постоянна
Удельная смертность m
Пороговая концентрация ресурса
Вопрос: найдите ошибку на правом графике.
Подсказка: как меняется скорость роста численности в зависимости от R - на левом графике? на правом графике?
Из Tilman 1982
Слайд 9Как определяется пороговая концентрация ресурса?
Расчет пороговой концентрации R*
b
bmax
k
bmax/2
R
Удельная рождаемость, [время]-1
Концентрация биогена
k
Уравнение Моно (Monod 1950)
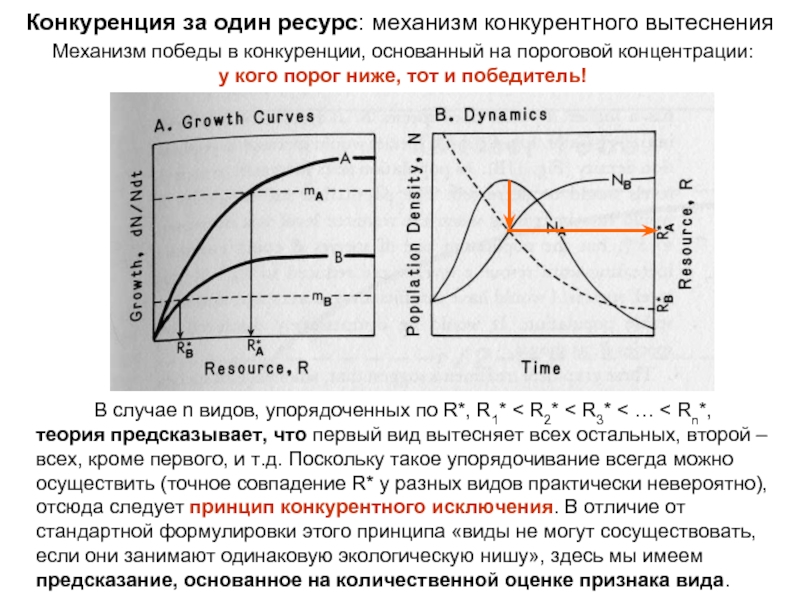
Слайд 10Механизм победы в конкуренции, основанный на пороговой концентрации:
у кого порог ниже,
Конкуренция за один ресурс: механизм конкурентного вытеснения
В случае n видов, упорядоченных по R*, R1* < R2* < R3* < … < Rn*,
теория предсказывает, что первый вид вытесняет всех остальных, второй – всех, кроме первого, и т.д. Поскольку такое упорядочивание всегда можно осуществить (точное совпадение R* у разных видов практически невероятно), отсюда следует принцип конкурентного исключения. В отличие от стандартной формулировки этого принципа «виды не могут сосуществовать, если они занимают одинаковую экологическую нишу», здесь мы имеем предсказание, основанное на количественной оценке признака вида.
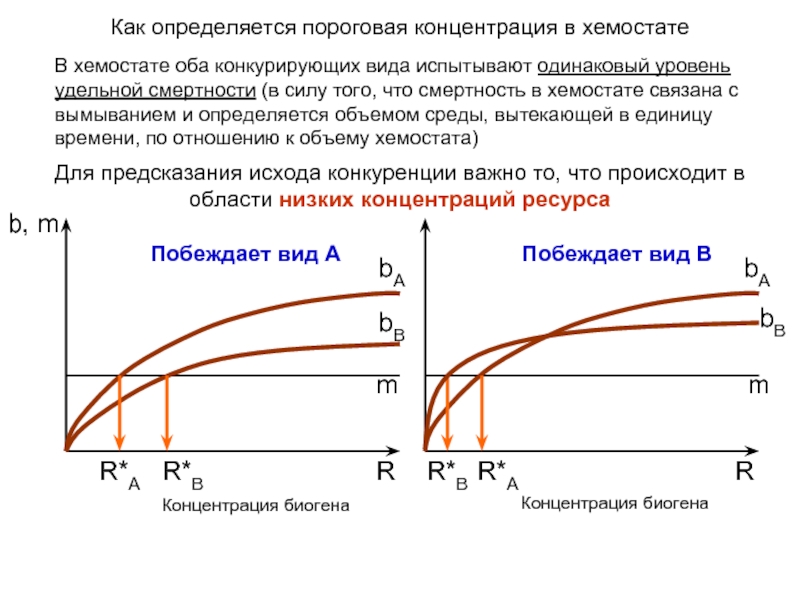
Слайд 11В хемостате оба конкурирующих вида испытывают одинаковый уровень удельной смертности (в
Как определяется пороговая концентрация в хемостате
b, m
R
Концентрация биогена
bA
m
bB
R*A
R*B
R
Концентрация биогена
bA
m
bB
R*B
R*A
Для предсказания исхода конкуренции важно то, что происходит в области низких концентраций ресурса
Побеждает вид A
Побеждает вид B
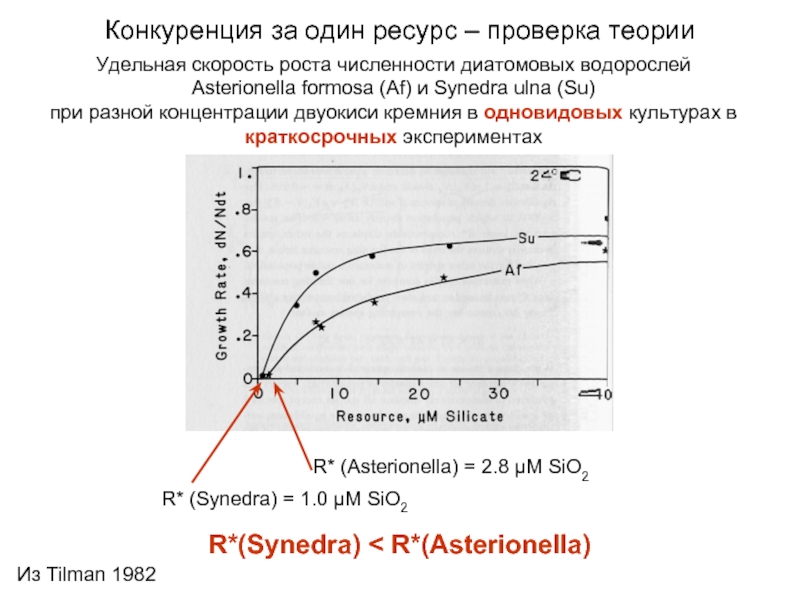
Слайд 12Удельная скорость роста численности диатомовых водорослей
Asterionella formosa (Af) и Synedra ulna
при разной концентрации двуокиси кремния в одновидовых культурах в краткосрочных экспериментах
Конкуренция за один ресурс – проверка теории
R* (Synedra) = 1.0 μM SiO2
R* (Asterionella) = 2.8 μM SiO2
R*(Synedra) < R*(Asterionella)
Из Tilman 1982
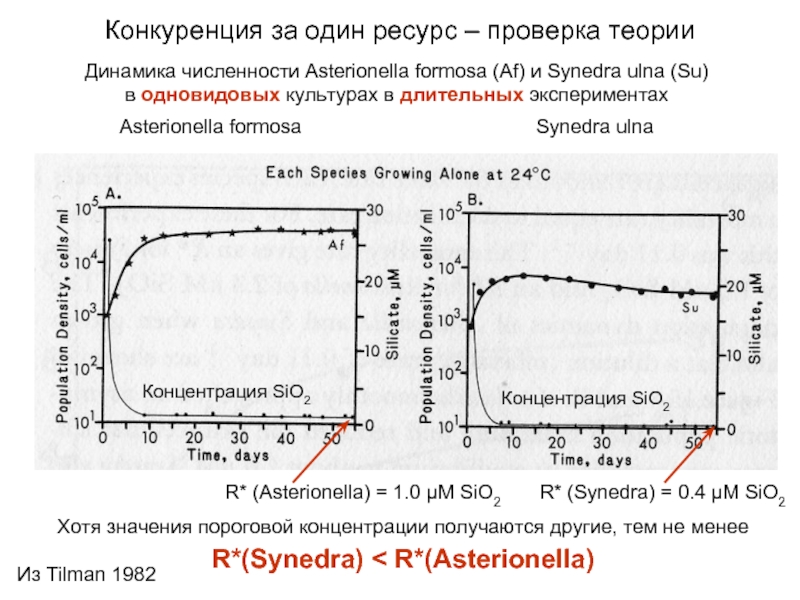
Слайд 13Динамика численности Asterionella formosa (Af) и Synedra ulna (Su)
в одновидовых культурах
Asterionella formosa
Synedra ulna
Концентрация SiO2
R* (Asterionella) = 1.0 μM SiO2
R* (Synedra) = 0.4 μM SiO2
Концентрация SiO2
Хотя значения пороговой концентрации получаются другие, тем не менее R*(Synedra) < R*(Asterionella)
Конкуренция за один ресурс – проверка теории
Из Tilman 1982
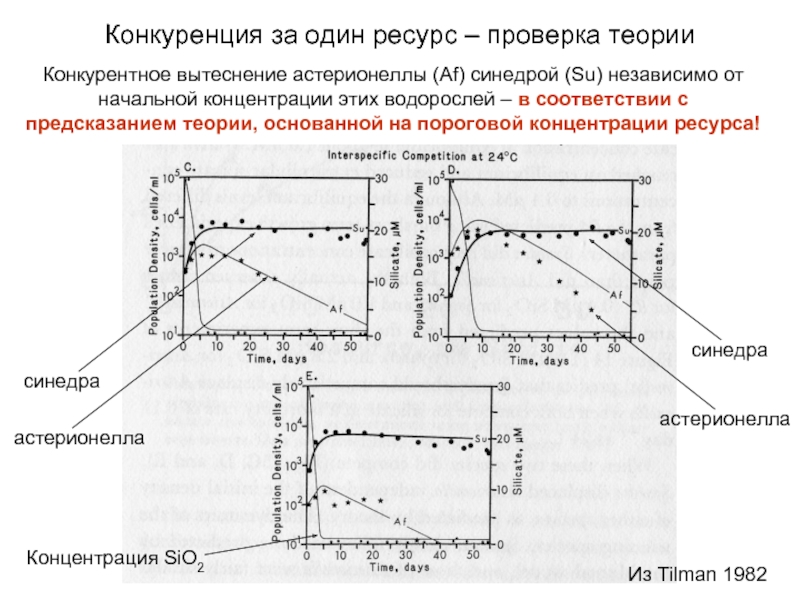
Слайд 14Конкурентное вытеснение астерионеллы (Af) синедрой (Su) независимо от начальной концентрации этих
синедра
астерионелла
Концентрация SiO2
синедра
астерионелла
Конкуренция за один ресурс – проверка теории
Из Tilman 1982
Слайд 15
R1
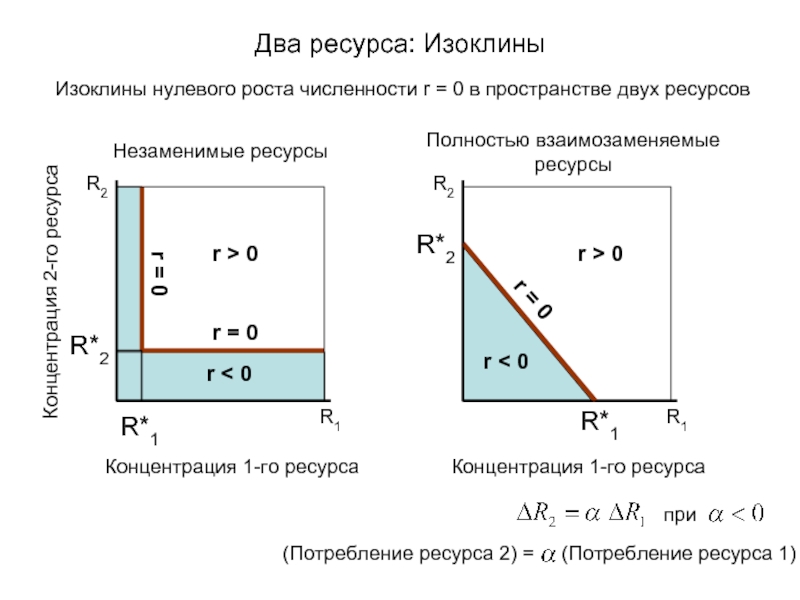
Изоклины нулевого роста численности r = 0 в пространстве двух ресурсов
Два
R1
R2
Незаменимые ресурсы
R2
Полностью взаимозаменяемые ресурсы
R*1
R*2
Концентрация 1-го ресурса
Концентрация 1-го ресурса
Концентрация 2-го ресурса
R*2
R*1
r > 0
r < 0
r = 0
r > 0
r = 0
r = 0
r < 0
(Потребление ресурса 2) = (Потребление ресурса 1)
при
Слайд 16N*c1
Вектор потребления C – это вектор, проекции которого на оси ресурсов
Два ресурса: Вектора C и U
Вектор потребления C, «вектор снабжения» U и ресурсная точка
R1
R2
C
N*c2
Вектор потребления C и вектор удельного
потребления
R2 или S2
a (S1- R1’)
Вектор поступления ресурсов U
и ресурсная точка (S1, S2)
R1 или S1
(S1,S2)
U
a (S2- R2’)
R1’
R2’
Слайд 17Один потребитель и два ресурса
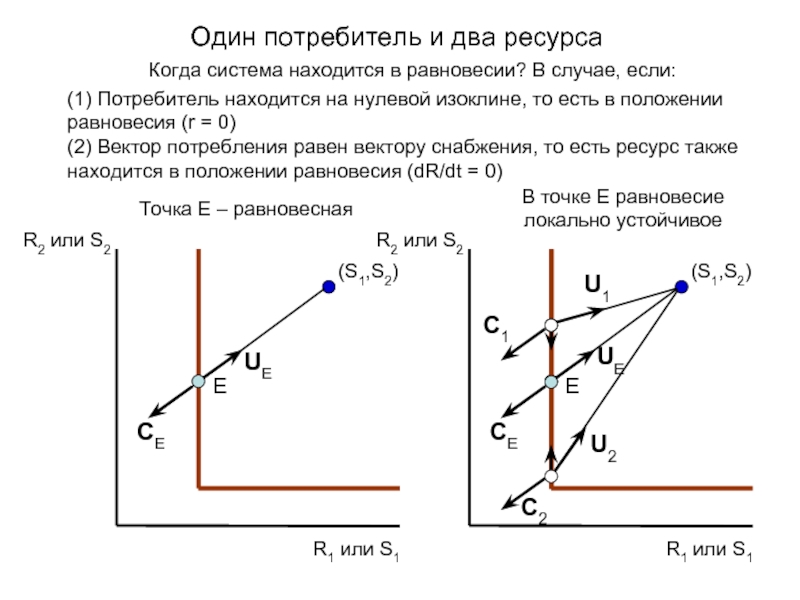
Когда система находится в равновесии? В случае,
(1) Потребитель находится на нулевой изоклине, то есть в положении равновесия (r = 0)
(2) Вектор потребления равен вектору снабжения, то есть ресурс также находится в положении равновесия (dR/dt = 0)
(S1,S2)
R1 или S1
R2 или S2
UE
CE
E
(S1,S2)
R1 или S1
UE
CE
E
Точка E – равновесная
В точке E равновесие локально устойчивое
U1
C1
U2
C2
R2 или S2
Слайд 18Как найти положение равновесия одного потребителя на двух ресурсах?
Построить нулевую
Построить вектор удельного потребления (в любой точке плоскости (R1, R2))
Нанести ресурсную точку
Провести через ресурсную точку линию, параллельную вектору потребления
Точка пересечения этой линии с нулевой изоклиной есть положение равновесия
Слайд 19Конкуренция двух видов (A и B) за два ресурса
R1
R2
A
B
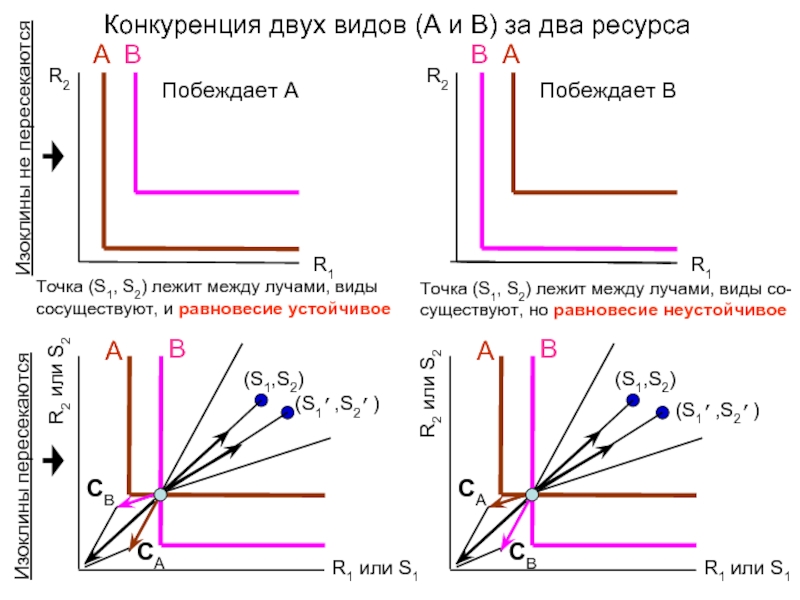
Побеждает A
A
B
Побеждает
R1 или S1
R2 или S2
A
B
R1
R2
CA
CB
(S1,S2)
(S1’,S2’)
R1 или S1
R2 или S2
A
B
CB
CA
(S1,S2)
(S1’,S2’)
Точка (S1, S2) лежит между лучами, виды со-существуют, но равновесие неустойчивое
Точка (S1, S2) лежит между лучами, виды сосуществуют, и равновесие устойчивое
Изоклины не пересекаются
Изоклины пересекаются
Слайд 20Конкуренция двух видов (A и B) за два ресурса
Условия сосуществования
(условия устойчивого
(1) Нулевые изоклины двух видов пересекаются. Точка пересечения нулевых изоклин – потенциальная точка равновесия
(2) Вектора потребления в точке пересечения изоклин наклонены таким образом, что для каждого вида выше скорость потребления того ресурса, который является для этого вида лимитирующим
(3) Ресурсная точка находится между лучами, являющимися продолжением векторов потребления
Все эти условия должны выполняться одновременно
Слайд 21Как определить, является ли равновесие устойчивым?
При отклонении от положения равновесия надо
Какой ресурс растет? Какой ресурс падает? Какой потребитель растет? Какой потребитель падает?
Оказывается, что положение равновесия устойчиво, если
(а) растет тот потребитель, который преимущественно потребляет тот ресурс, которого стало больше
(б) падает тот потребитель, который преимущественно потребляет тот ресурс, которого стало меньше
Конкуренция двух видов (A и B) за два ресурса
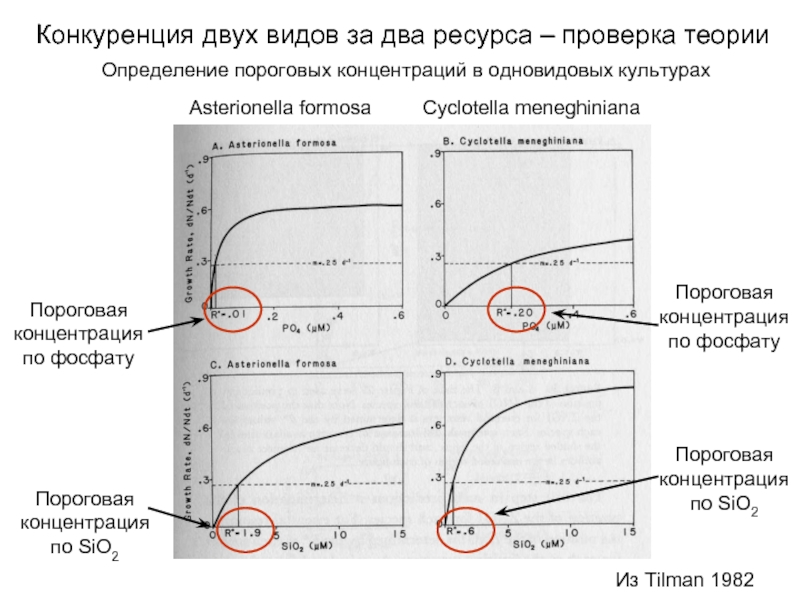
Слайд 22Конкуренция двух видов за два ресурса – проверка теории
Asterionella formosa
Cyclotella meneghiniana
Определение
Пороговая концентрация по фосфату
Пороговая концентрация по фосфату
Пороговая концентрация по SiO2
Пороговая концентрация по SiO2
Из Tilman 1982
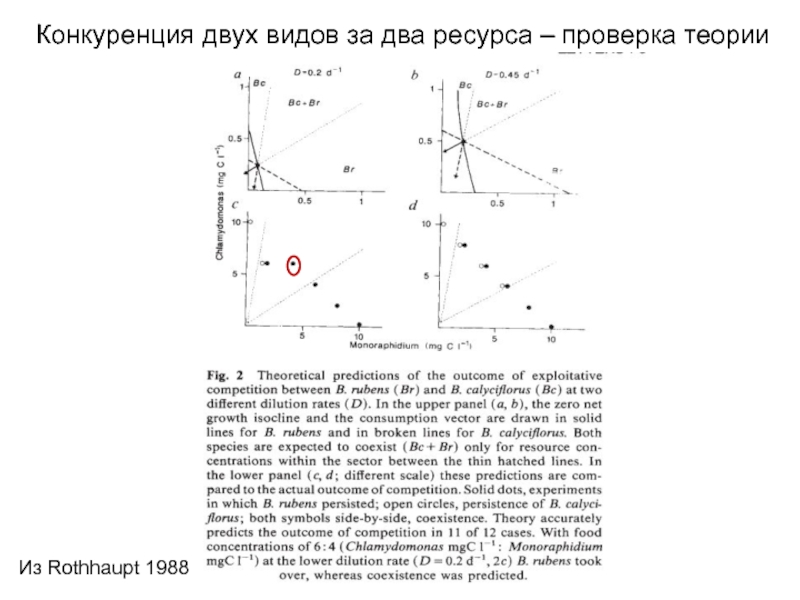
Слайд 23Конкуренция двух видов за два ресурса – проверка теории
График нулевых изоклин,
Asterionella formosa
Cyclotella meneghiniana
PO4
SiO2
SiO2
rA > 0
rC > 0
Из Tilman 1982
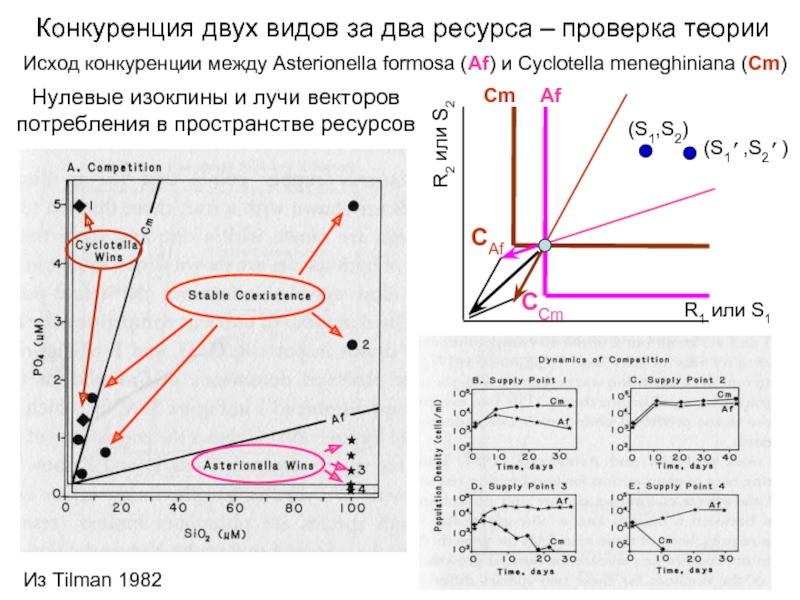
Слайд 24Конкуренция двух видов за два ресурса – проверка теории
Исход конкуренции между
Нулевые изоклины и лучи векторов потребления в пространстве ресурсов
R1 или S1
R2 или S2
CCm
CAf
(S1,S2)
(S1’,S2’)
Cm
Af
Из Tilman 1982
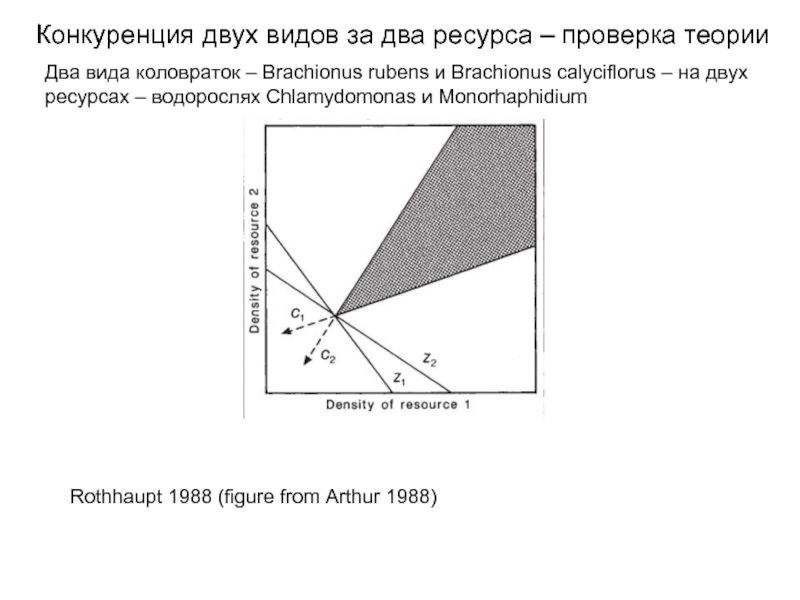
Слайд 25Rothhaupt 1988 (figure from Arthur 1988)
Конкуренция двух видов за два ресурса
Два вида коловраток – Brachionus rubens и Brachionus calyciflorus – на двух ресурсах – водорослях Chlamydomonas и Monorhaphidium
Слайд 27Сосуществование многих видов на ограниченном числе ресурсов
и парадокс обогащения:
Объяснение в рамках
Проблема: несмотря на принцип конкурентного исключения, потребителей много
Решения:
1) Диверсификация ниш
Критика: (а) концепция ниши слишком расплывчата (даже между двумя особями легко найти различие в их предпочтениях, тем более это можно сделать между видами), (б) число существенных ресурсов, по кр. мере для растений, невелико (свет, вода, углекислый газ, N, P, K, Mg, Ca, ~15 микроэлементов)
2) Неравновесная динамика (непостоянство параметров уравнений во времени, вызванное нарушениями среды)
Критика: параметры уравнений плохо поддаются количественной оценке
Проблема: с увеличением концентрации ресурса число сосуществующих видов-потребителей уменьшается
Решение:
Дестабилизация системы ресурс-потребитель при высокой концентрации ресурса (из-за особой формы нулевой изоклины для жертвы - она имеет «горб») (Rosenzweig 1971)
Критика: объяснение работает только для одного потребителя, а их много
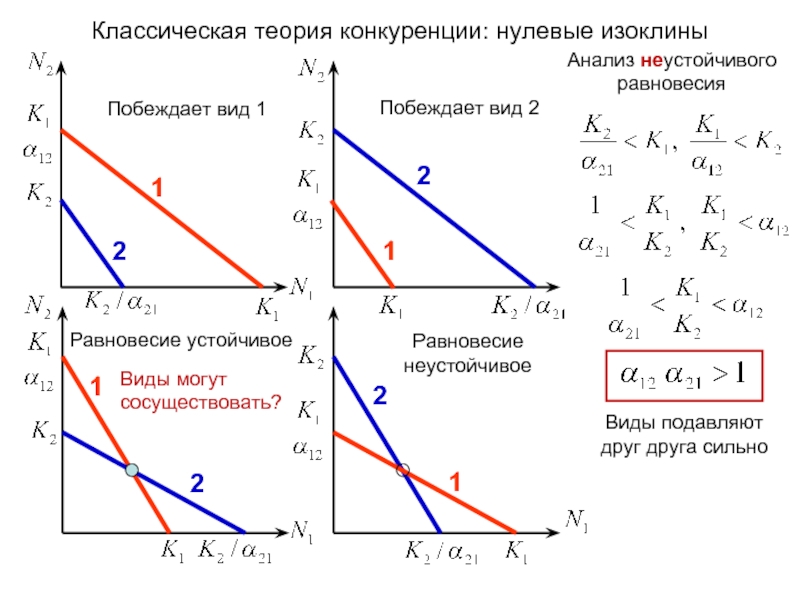
Слайд 28S – максимальная концентрация ресурса в данном местообитании, «емкость среды»
(S1,S2) –
Круги – контуры место-обитаний с данной пространственной не-однородностью ресурсов
Сосуществование многих видов и парадокс обогащения:
Объяснение, основанное на ресурсной теории конкуренции и пространственной неоднородности ресурсов
Семь видов (a, b, c, d, e, f, g) конкурируют за два ресурса (1 и 2). Линии, образующие прямой угол, представляют нулевые изоклины для каждого из семи видов в пространстве ресурсов. Наклонные линии представляют продолжения векторов потребления в точке равновесия пары видов. Сектора (a+b и т.д.) есть множество точек (совокупность местообитаний), в которых «емкость среды» такова, что в них возможно сосуществование соответствующей пары видов (таких секторов шесть). Из Tilman 1982.
Концентрация ресурса 1, R1
Концентрация ресурса 2, R2
Следствия:
1) В бедной среде всего на двух ресурсах может сосуществовать много видов
2) С обогащением среды число видов уменьшается
3) Видовой состав зависит от того, в каком направлении идет обогащение среды


![«Нам остается теперь рассмотреть второй этап конкуренции, т.е. непосредственное вытеснение одного вида другим. […] В](/img/tmb/2/153908/eec71d4e48e84b46ad7817013dd7189a-800x.jpg)

![Как определяется пороговая концентрация ресурса?Расчет пороговой концентрации R*bbmaxkbmax/2RУдельная рождаемость, [время]-1Концентрация биогенаk – константа полунасыщенияУравнение Моно](/img/tmb/2/153908/63cf61985ebd54367f94f446667ba579-800x.jpg)