ГИА - 2014
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вероятности событий. Подготовка к ГИА - 2014 презентация
Содержание
- 1. Вероятности событий. Подготовка к ГИА - 2014
- 3. Вероятность – это число от 0 до
- 4. №1. На тарелке лежат
- 5. №1. Решение:
- 6. №2. На
- 7. №2. Решение:
- 8. №3. В лыжных
- 9. №3. Решение: Общее
- 10. №4. Бросают два
- 11. Таблица элементарных событий
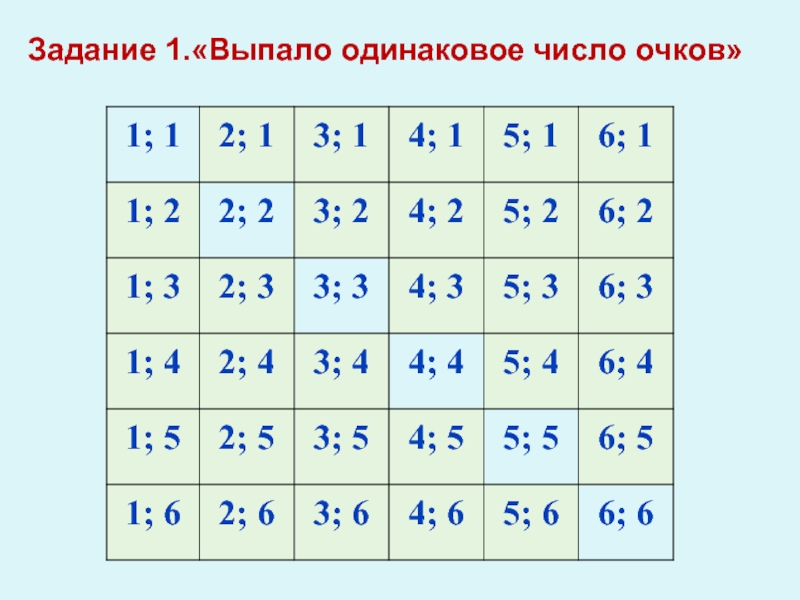
- 12. Задание 1.«Выпало одинаковое число очков»
- 13. Задание 1.«Выпало одинаковое число очков»
- 14. Задание 2. « Сумма очков равна 7»
- 15. Задание 2. « Сумма очков равна 7»
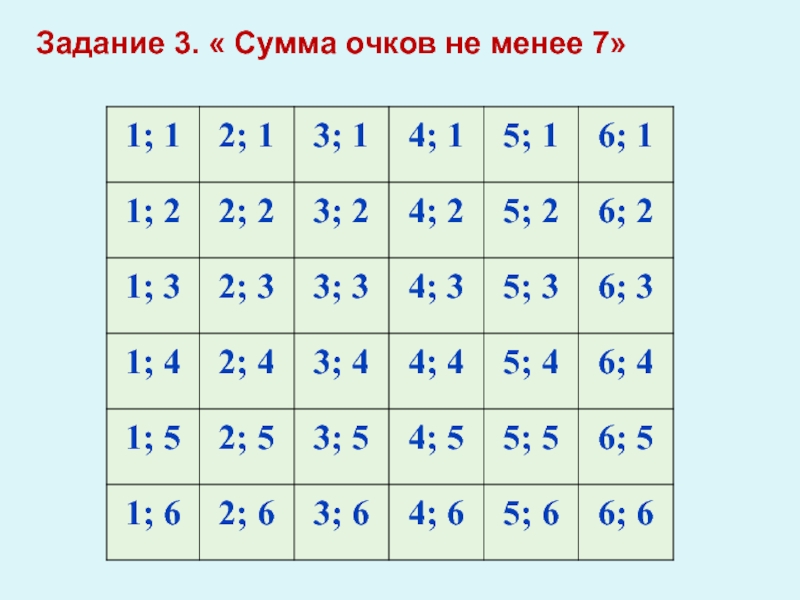
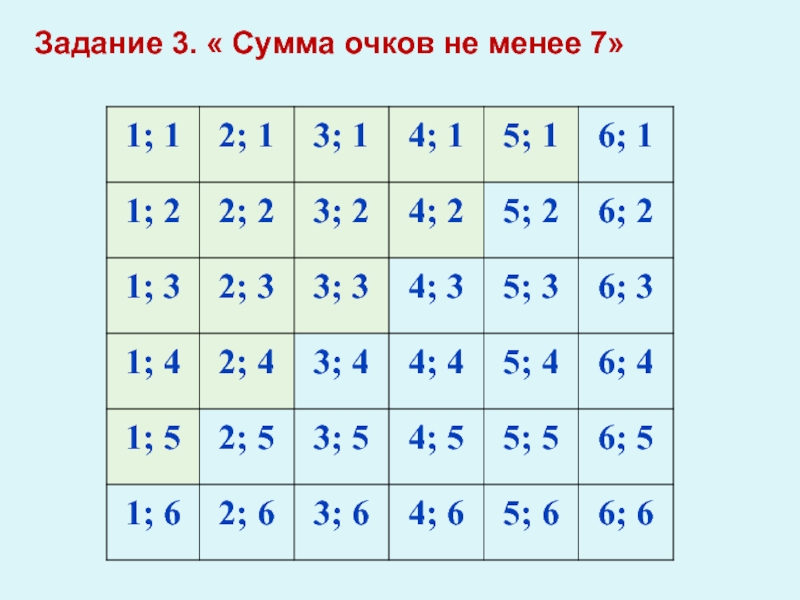
- 16. Задание 3. « Сумма очков не менее 7»
- 17. Задание 3. « Сумма очков не менее 7»
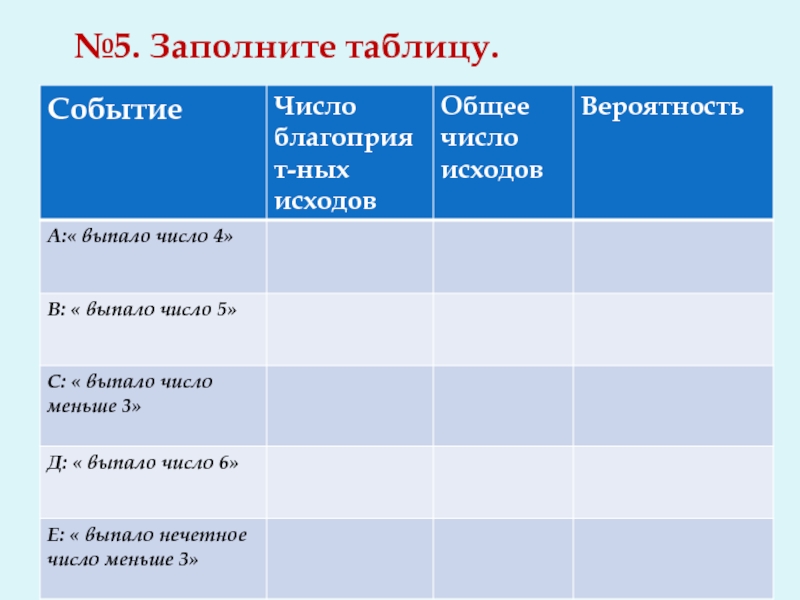
- 18. №5. Заполните таблицу.
- 19. №6.
- 20. №7. Игральный кубик бросают два
- 21. Решение: событие А: общее число исходов-36,
- 22. №8. Для экзамена
- 23. №9 В мешке
- 24. №10. Какова
- 25. №11 В коробке лежат 30
- 26. №11. Решение: Общее число равновозможных
- 27. №12 На подносе лежат 20
- 28. №13 В детский сад привезли
- 29. №14 Монета брошена 2 раза.
- 30. №14. Решение: Общее число равновозможных исходов:
- 31. №15 Монета брошена 2 раза. Какова вероятность
- 32. Успехов на экзаменах !
Вероятностью Р наступления случайного события А называется отношение m к n, где n – число всех возможных исходов
Слайд 2
Вероятностью Р наступления случайного события А называется отношение m к n, где n – число всех возможных исходов , а m – число всех благоприятных исходов.
Слайд 3Вероятность – это число от 0 до 1. Вероятность равна 0,
если событие невозможное.
Вероятность равна 1, если событие достоверное.
Слайд 4№1.
На тарелке лежат пирожки, одинаковые на вид: 4
с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Слайд 5 №1. Решение:
Общее число равновозможных исходов: 15
Число благоприятных исходов: 3
Вероятность = 3 : 15 = 3 /15 = 0,2
Ответ: 0,2
Слайд 6 №2.
На книжной полке стоят 20 книг, из них 3
справочника. Какова вероятность , что случайно взятая с полки книга не окажется справочником?
Слайд 7 №2. Решение:
Общее число равновозможных исходов: 20
Число благоприятных исходов 20-3=17
Вероятность
=17 : 20 = 17/20 = 0,85
Ответ: 0,85
Ответ: 0,85
Слайд 8№3.
В лыжных гонках участвуют 15 спортсменов из
России, 2 спортсмена из Норвегии и 3 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Слайд 9 №3. Решение:
Общее число равновозможных исходов: 20
Число благоприятных исходов: 2
+ 3 = 5
Вероятность = 5 : 20 = 5 /20 = 0,25
Ответ: 0,25
Вероятность = 5 : 20 = 5 /20 = 0,25
Ответ: 0,25
Слайд 10 №4.
Бросают два игральных кубика. В таблице покажите штриховкой события,
благоприятствующие событиям:
Слайд 19№6.
Первый
кубик
1 2 3 4 5 6
в 1
т 2
о 3
р 4
о 5
й 6
1 2 3 4 5 6
в 1
т 2
о 3
р 4
о 5
й 6
Семен и Иван играют. Каждый бросает игральный кубик два раза. Выигрывает тот, у кого выпавшая сумма очков больше. Если суммы очков равны, игра оканчивается вничью. Первым бросал кости Семен, и у него выпало 2 очка и 3 очка. Теперь бросает кости Иван.
а) В таблице элементарных событий укажите (штриховкой) элементарные события, благоприятствующие событию «Выиграет Иван».
б) Найдите вероятность события «Иван выиграет».
Слайд 20№7.
Игральный кубик бросают два раза. Какое событие более вероятно:
А: «Оба
раза выпало 6 очков»;
В: «В первый раз выпала 3 очка, во второй 5 очков» ;
С: «Один раз выпало 3 очка, один раз 5 очков»?
В: «В первый раз выпала 3 очка, во второй 5 очков» ;
С: «Один раз выпало 3 очка, один раз 5 очков»?
Слайд 21Решение:
событие А: общее число исходов-36, число благоприятствующих исходов- 1 (6;6)
Р
= 1/36.
событие В: общее число исходов-36, число благоприятствующих исходов- 1 (3;5)
Р = 1/36.
событие С: общее число исходов-36, число благоприятствующих исходов- 2 (3;5 и 5;3)
Р = 2/36=1/18.
Ответ: событие С.
событие В: общее число исходов-36, число благоприятствующих исходов- 1 (3;5)
Р = 1/36.
событие С: общее число исходов-36, число благоприятствующих исходов- 2 (3;5 и 5;3)
Р = 2/36=1/18.
Ответ: событие С.
Слайд 22 №8.
Для экзамена подготовили билеты с номерами от 1 до
50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер? ( В ответе укажите результат, округленный до сотых )
Ответ:0,18
Ответ:0,18
Слайд 23№9
В мешке содержатся жетоны с номерами от 5 до
54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число? (В ответе укажите результат, округленный до сотых)
Ответ: 0,16
Ответ: 0,16
Слайд 24 №10.
Какова вероятность того, что случайно выбранное натуральное число
от 15 до 29 делится на 5?
Ответ: 0,2
Ответ: 0,2
Слайд 25 №11
В коробке лежат 30 шаров белого, синего, красного и зеленого
цвета. Известно, что вероятность вынуть красный шар равна 0,6. Сколько в коробке красных шаров?
Слайд 26 №11. Решение:
Общее число равновозможных исходов: 30
число благоприятных исходов: х
Вероятность
= х : 30, а по условию она равна 0,6.Составим уравнение
х : 30 = 0,6
х = 30 * 0,6
х = 18
Значит, в коробке 18 красных шаров.
Ответ: 18
х : 30 = 0,6
х = 30 * 0,6
х = 18
Значит, в коробке 18 красных шаров.
Ответ: 18
Слайд 27№12
На подносе лежат 20 одинаковых на вид пирожков: с
мясом, с капустой, с картошкой и с повидлом. Известно, что вероятность взять пирожок с повидлом равна 0,4. Сколько пирожков с повидлом на подносе?
Ответ:8
Ответ:8
Слайд 28№13
В детский сад привезли 80 мячей синего и зеленого
цвета. Вероятность того, что старшая группа получит все мячи синего цвета равна 0,15. Сколько зеленых мячей привезли в детский сад?
Ответ: 68
Ответ: 68
Слайд 30 №14. Решение:
Общее число равновозможных исходов: 4 ( ОО,ОР,
РО,РР )
Число благоприятных
исходов: 1 (ОО )
Вероятность = 1 : 4 = 1 /4 = 0, 25
Ответ: 0,25
Вероятность = 1 : 4 = 1 /4 = 0, 25
Ответ: 0,25
Слайд 31№15
Монета брошена 2 раза. Какова вероятность того, что орел выпадет хотя
бы один раз?
Ответ:0,75
Ответ:0,75
