Графы презентация

Содержание

1. Графы
2. Кенигсбергские мосты К
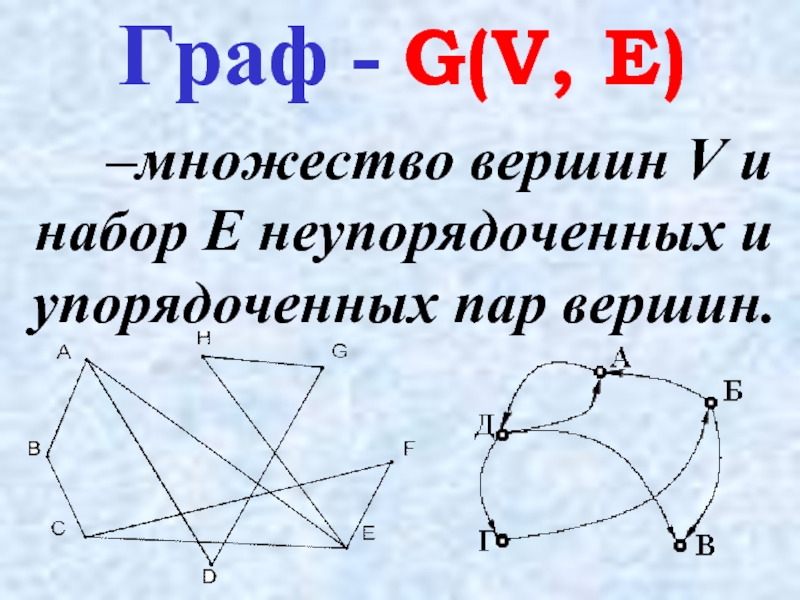
3. –множество вершин V и набор E неупорядоченных
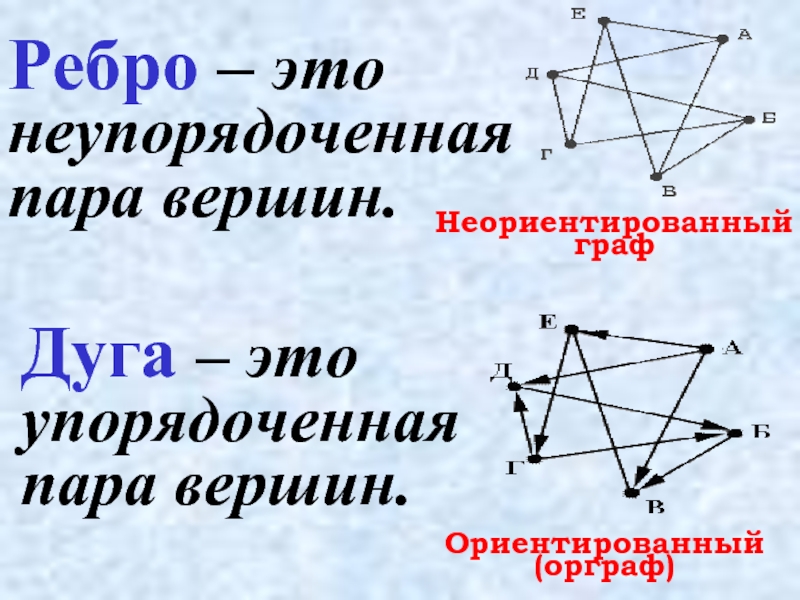
4. Ребро – это неупорядоченная пара вершин. Дуга
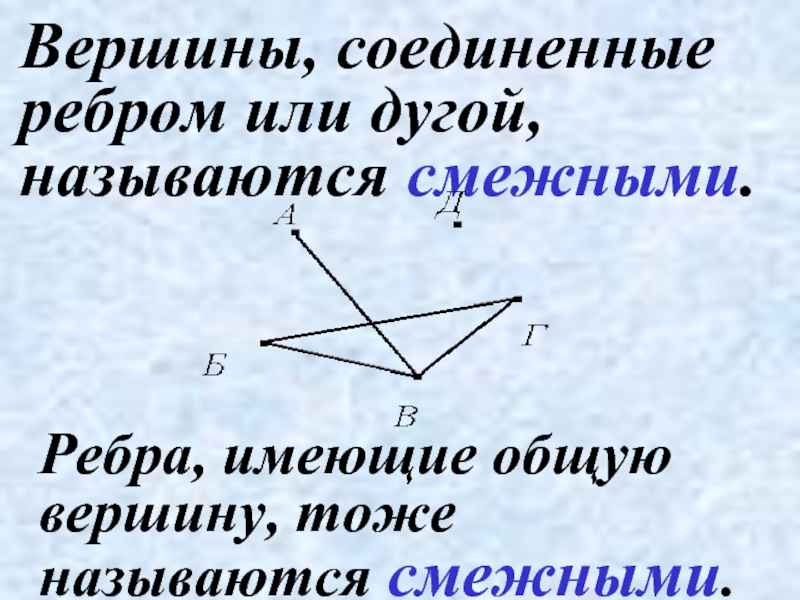
5. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, тоже называются смежными.
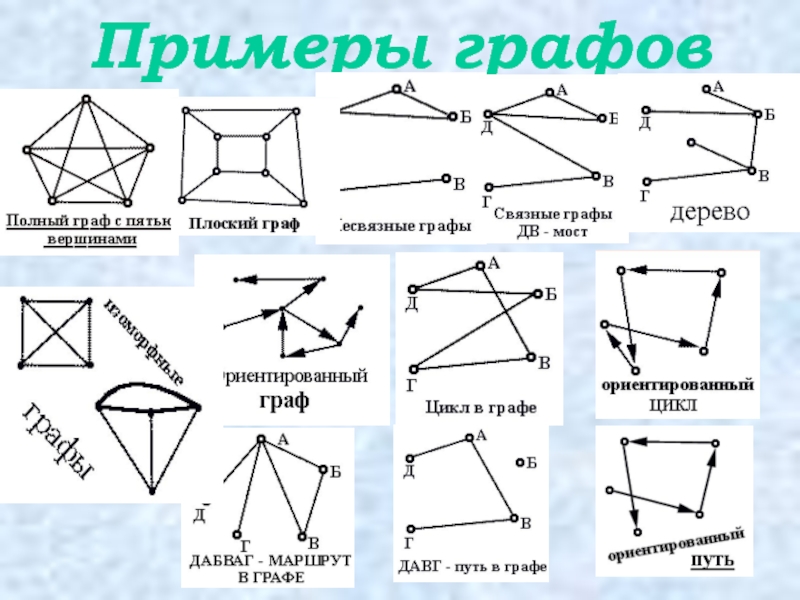
6. Примеры графов
7. Матрица смежности Перечень списков смежных вершин Представление графа в памяти ЭВМ
8. – это двумерный массив А размерностью N
9. – это N списков, каждый из которых
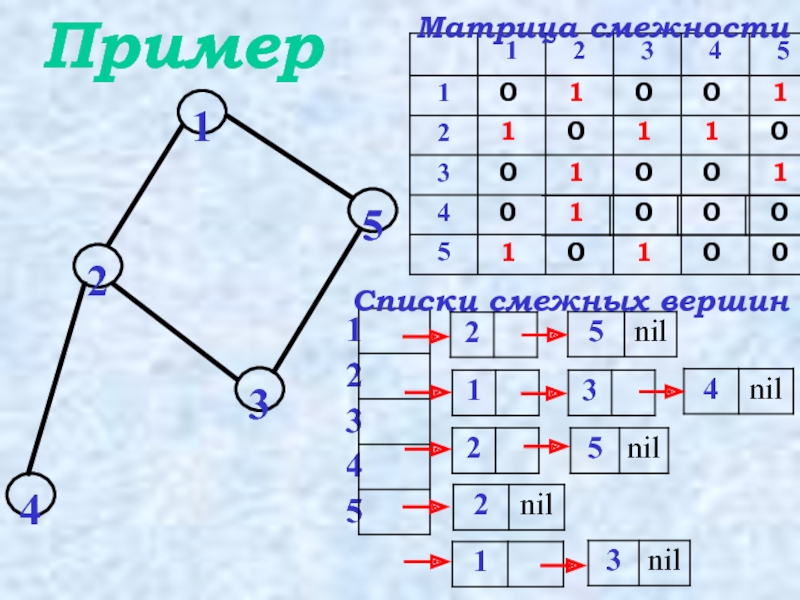
10. Пример Матрица смежности Списки смежных вершин
11. Алгоритмы поиска в графе
12. Начиная с первой вершины идем «вглубь», пока
13. Начиная с начальной вершины проверяются все вершины,
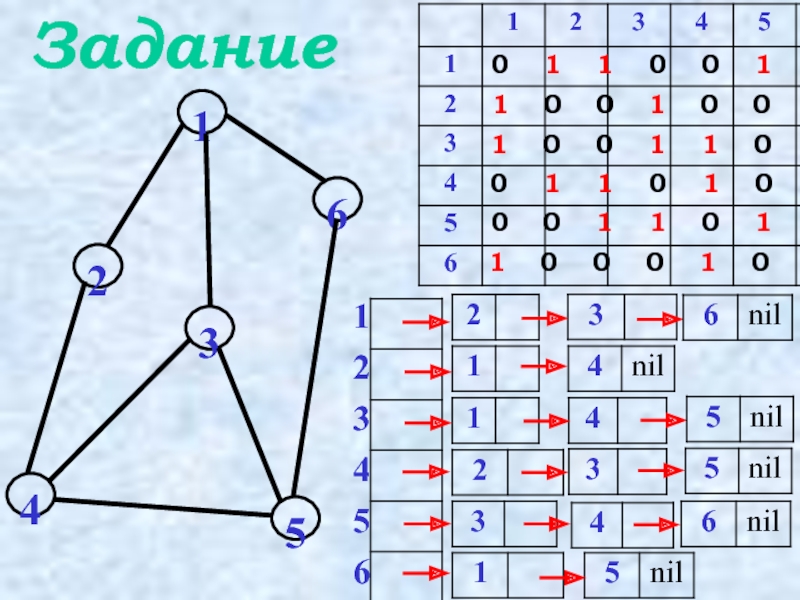
14. Задание
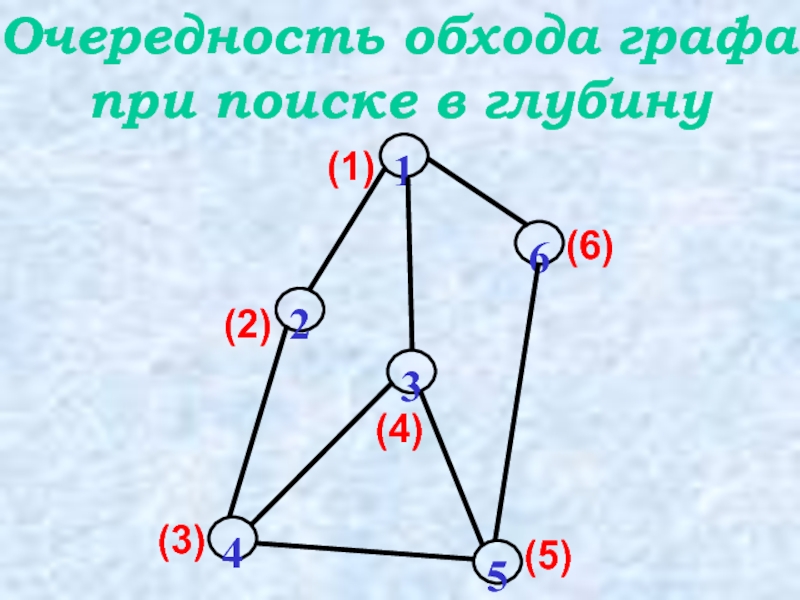
15. Очередность обхода графа при поиске в глубину (1) (2) (3) (4) (5) (6)
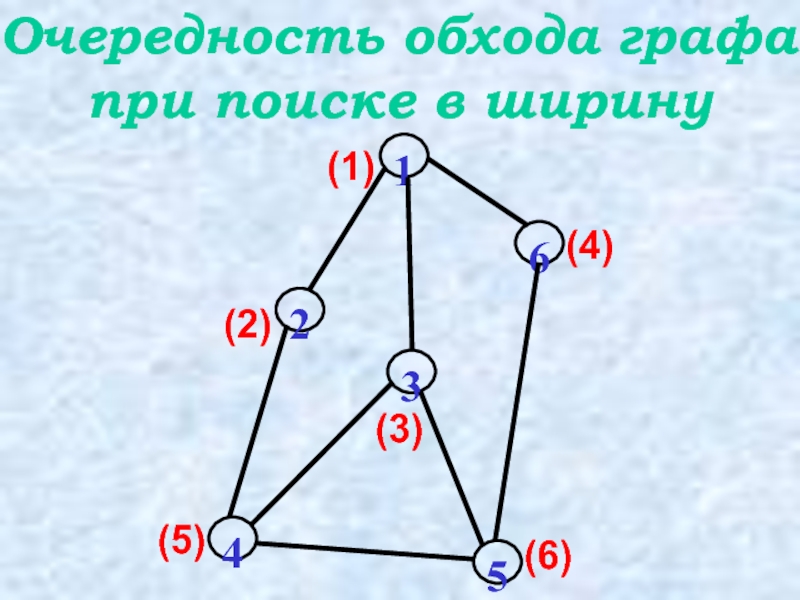
16. Очередность обхода графа при поиске в ширину (1) (2) (5) (3) (6) (4)
17. Деревья
18. – это связный граф без циклов.
19. – это такой граф, ребрам или дугам
20. – это подграф, включающий все вершины исходного
21. γ = m – n +1
22. γ = ? γ = 5 – 5 + 1= 1
23. Из графа удаляются все ребра и получается
24. Ребра последовательно по возрастанию их весов включаются
25. Примеры неориентированных графов
26. Примеры ориентированных графов
27. Примеры взвешенных графов
28. Примеры деревьев

Слайд 1Графы

Слайд 2Кенигсбергские мосты
К XVIII веку через реку, на

которой стоял город Кенигсберг (ныне Калининград), было построено 7 мостов, которые связывали с берегами и друг с другом два острова, расположенные в пределах города.
Задача: нужно пройти (если это возможно) по всем семи мостам так, чтобы на каждом из них побывать лишь по одному разу и вернуться к тому месту, откуда начал маршрут.

Термин «граф» впервые ввел в 1936 г. венгерский математик Д. Кениг, хотя задачи по теории графов решал еще Л.Эйлер в XVIII веке.

Из истории теории графов

Слайд 3 –множество вершин V и набор E неупорядоченных и упорядоченных пар вершин.

Граф - G(V, E)

Слайд 4Ребро – это неупорядоченная пара вершин.
Дуга – это упорядоченная пара вершин.

Неориентированный граф

Ориентированный (орграф)

Слайд 5Вершины, соединенные ребром или дугой, называются смежными.
Ребра, имеющие общую вершину, тоже

называются смежными.

Слайд 6Примеры графов

Слайд 7 Матрица смежности
Перечень списков смежных вершин

Представление графа в памяти ЭВМ

Слайд 8– это двумерный массив А размерностью N × N,
где N

– количество вершин графа.

Матрица смежности

Слайд 9– это N списков, каждый из которых содержит номера всех смежных

вершин.

Перечень списков смежных вершин

Указатели на первые элементы списков объединены в массив.

Слайд 10Пример
Матрица смежности
Списки смежных вершин

Слайд 11Алгоритмы поиска в графе

Слайд 12Начиная с первой вершины идем «вглубь», пока это возможно. Выбирается вершина,

смежная с предыдущей, и процесс повторяется.
Если на очередном шаге оказалось, что нет непросмотренных вершин, связанных с текущей, то выполняется возврат к предыдущей и ищется новая вершина, связанная с ней, и так до тех пор, пока не вернемся к начальной вершине.

Поиск в глубину

(1)

(2)

(3)

(4)

(5)

Очередность просмотра вершин

Слайд 13Начиная с начальной вершины проверяются все вершины, смежные с данной. Их

номера заносятся в очередь.
Далее процесс продолжается с первой из вершин, записанной в очереди. И до тех пор, пока очередь не окажется пустой.

Поиск в ширину

(1)

(2)

(4)

(3)

(5)

Очередность просмотра вершин

Слайд 14Задание

Слайд 15Очередность обхода графа при поиске в глубину
(1)
(2)
(3)
(4)
(5)
(6)

Слайд 16Очередность обхода графа при поиске в ширину
(1)
(2)
(5)
(3)
(6)
(4)

Слайд 17Деревья

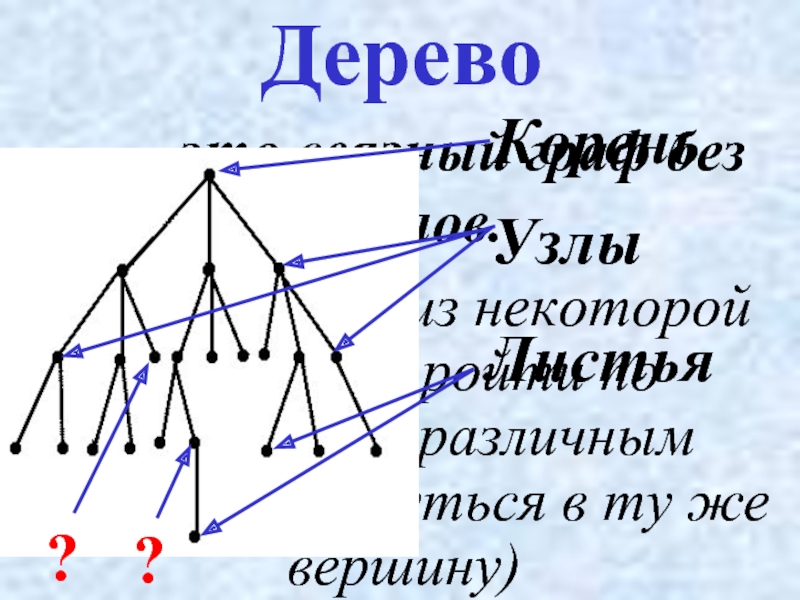
Слайд 18 – это связный граф без циклов.
(В нем нельзя из некоторой

вершины пройти по нескольким различным ребрам и вернуться в ту же вершину)

Дерево

Корень

Узлы

Листья

Слайд 19 – это такой граф, ребрам или дугам которого поставлены в соответствие

числовые величины (вес ребер).

Взвешенный граф

Матрица смежности

Слайд 20 – это подграф, включающий все вершины исходного графа, каждая вершина которого

достижима из любой другой и не содержащий циклов.

Остовное связное дерево

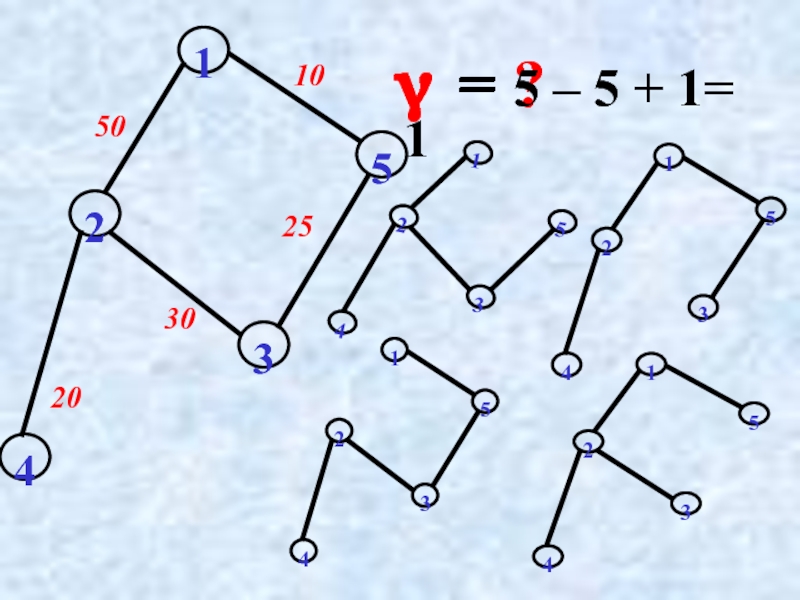
Слайд 21 γ = m – n +1 , где
m – количество

ребер,
n – количество вершин

показывающего, сколько ребер графа нужно удалить, чтобы в нем не осталось ни одного цикла.

Преобразование графа в остовное связное дерево с помощью цикломатического числа γ ,

Слайд 22γ = ?
γ = 5 – 5 + 1= 1

Слайд 23Из графа удаляются все ребра и получается остовной подграф, где все

вершины изолированы.

Построение остовного связного дерева минимального веса (алгоритм Крускала)

Слайд 24Ребра последовательно по возрастанию их весов включаются в остовное дерево.
Алгоритм заканчивается,

когда все вершины будут объединены в одно связное множество, оставшиеся ребра не включаются в остовное дерево.

Слайд 25Примеры неориентированных графов

Слайд 26Примеры ориентированных графов

Слайд 27Примеры взвешенных графов

Слайд 28Примеры деревьев

Скачать презентацию

Графы презентация

Содержание

Слайд 1Графы

Слайд 2Кенигсбергские мосты
К XVIII веку через реку, на

Слайд 3 –множество вершин V и набор E неупорядоченных и упорядоченных пар вершин.

Слайд 4Ребро – это неупорядоченная пара вершин.
Дуга – это упорядоченная пара вершин.

Слайд 5Вершины, соединенные ребром или дугой, называются смежными.
Ребра, имеющие общую вершину, тоже

Слайд 6Примеры графов

Слайд 7 Матрица смежности
Перечень списков смежных вершин

Представление графа в памяти ЭВМ

Слайд 8– это двумерный массив А размерностью N × N,
где N

Слайд 9– это N списков, каждый из которых содержит номера всех смежных

Слайд 10Пример
Матрица смежности
Списки смежных вершин

Слайд 11Алгоритмы поиска в графе

Слайд 12Начиная с первой вершины идем «вглубь», пока это возможно. Выбирается вершина,

Слайд 13Начиная с начальной вершины проверяются все вершины, смежные с данной. Их

Слайд 14Задание

Слайд 15Очередность обхода графа при поиске в глубину
(1)
(2)
(3)
(4)
(5)
(6)

Слайд 16Очередность обхода графа при поиске в ширину
(1)
(2)
(5)
(3)
(6)
(4)

Слайд 17Деревья

Слайд 18 – это связный граф без циклов.
(В нем нельзя из некоторой

Слайд 19 – это такой граф, ребрам или дугам которого поставлены в соответствие

Слайд 20 – это подграф, включающий все вершины исходного графа, каждая вершина которого

Слайд 21 γ = m – n +1 , где
m – количество

Слайд 22γ = ?
γ = 5 – 5 + 1= 1

Слайд 23Из графа удаляются все ребра и получается остовной подграф, где все

Слайд 24Ребра последовательно по возрастанию их весов включаются в остовное дерево.
Алгоритм заканчивается,

Слайд 25Примеры неориентированных графов

Слайд 26Примеры ориентированных графов

Слайд 27Примеры взвешенных графов

Слайд 28Примеры деревьев

Обратная связь

Что такое ThePresentation.ru?

Графы презентация

Содержание

Слайд 1Графы

Слайд 2Кенигсбергские мосты К XVIII веку через реку, на

Слайд 3 –множество вершин V и набор E неупорядоченных и упорядоченных пар вершин.

Слайд 4Ребро – это неупорядоченная пара вершин.Дуга – это упорядоченная пара вершин.

Слайд 5Вершины, соединенные ребром или дугой, называются смежными.Ребра, имеющие общую вершину, тоже

Слайд 6Примеры графов

Слайд 7 Матрица смежности Перечень списков смежных вершинПредставление графа в памяти ЭВМ

Слайд 8– это двумерный массив А размерностью N × N, где N

Слайд 9– это N списков, каждый из которых содержит номера всех смежных

Слайд 10ПримерМатрица смежностиСписки смежных вершин

Слайд 11Алгоритмы поиска в графе

Слайд 12Начиная с первой вершины идем «вглубь», пока это возможно. Выбирается вершина,

Слайд 13Начиная с начальной вершины проверяются все вершины, смежные с данной. Их

Слайд 14Задание

Слайд 15Очередность обхода графа при поиске в глубину(1)(2)(3)(4)(5)(6)

Слайд 16Очередность обхода графа при поиске в ширину(1)(2)(5)(3)(6)(4)

Слайд 17Деревья

Слайд 18 – это связный граф без циклов. (В нем нельзя из некоторой

Слайд 19 – это такой граф, ребрам или дугам которого поставлены в соответствие

Слайд 20 – это подграф, включающий все вершины исходного графа, каждая вершина которого

Слайд 21 γ = m – n +1 , гдеm – количество

Слайд 22γ = ?γ = 5 – 5 + 1= 1

Слайд 23Из графа удаляются все ребра и получается остовной подграф, где все

Слайд 24Ребра последовательно по возрастанию их весов включаются в остовное дерево.Алгоритм заканчивается,

Слайд 25Примеры неориентированных графов

Слайд 26Примеры ориентированных графов

Слайд 27Примеры взвешенных графов

Слайд 28Примеры деревьев

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2Кенигсбергские мосты
К XVIII веку через реку, на

Слайд 4Ребро – это неупорядоченная пара вершин.
Дуга – это упорядоченная пара вершин.

Слайд 5Вершины, соединенные ребром или дугой, называются смежными.
Ребра, имеющие общую вершину, тоже

Слайд 7 Матрица смежности
Перечень списков смежных вершин

Представление графа в памяти ЭВМ

Слайд 8– это двумерный массив А размерностью N × N,
где N

Слайд 10Пример
Матрица смежности
Списки смежных вершин

Слайд 15Очередность обхода графа при поиске в глубину
(1)
(2)
(3)
(4)
(5)
(6)

Слайд 16Очередность обхода графа при поиске в ширину
(1)
(2)
(5)
(3)
(6)
(4)

Слайд 18 – это связный граф без циклов.
(В нем нельзя из некоторой

Слайд 21 γ = m – n +1 , где
m – количество

Слайд 22γ = ?
γ = 5 – 5 + 1= 1

Слайд 24Ребра последовательно по возрастанию их весов включаются в остовное дерево.
Алгоритм заканчивается,