Матюшкин И.В., кфмн,
ОАО «НИИ молекулярной электроники», Москва, Зеленоград
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение клеточных автоматов в математическом моделировании технологии микро- и наноэлектроники презентация
Содержание
- 1. Применение клеточных автоматов в математическом моделировании технологии микро- и наноэлектроники
- 2. Содержание Предварительные замечания Семантика клеточных автоматов (КА)
- 3. I. Предварительные замечания В России наибольший опыт
- 4. Поскольку все величины дискретны, масштабы должны быть
- 5. В.К. Ванаг Исследование пространственно распределённых динамических систем методами
- 6. массив клеток разбит на множество конечных, отдельных
- 7. II. Семантика КА на гексагональной сетке Специфика
- 8. Снежинкоподобные формы роста кристалла в растворе хлорида
- 9. Таблица. Правила перехода, задаваемых kcode = 0022000220022001122200021210.
- 10. «Игровые» КА обычно разыгрываются на бесконечной доске,
- 11. Симметричные изомероподобные паттерны в ГС-аналоге КА Конвэя.
- 12. 0101002002210000101122201000; 1200122011001110101120001000; 0010122201010210211120001000; 1201010010210122110120001000; 0102222210111010210120001000; 2221010222010101000120101000;
- 13. КА на ГС тяготеют к симметричным фигурам
- 14. Интерес к КА модели на сфере обусловлен
- 15. 15 Стратегия масштабирования икосаэдрической треугольной сетки (показаны
- 16. Фуллереновая сетка Существуют тетраэдрические (Td) и икосаэдрические
- 17. 17 Кубированная сфера Такая сетка строится
- 18. Модель гетерофазной бимолекулярной реакции
- 19. Таблица парных переходов 19 Примечание: строки
- 20. Области реагента А в реагенте
- 21. КА на фуллерене С60 на 0,
- 22. Зависимость изолированных ячеек каждого состояния/цвета от номера
- 23. III. КА-модель ионной имплантации: концептуальный анализ и
- 24. Алгоритм общей модели Разделив переменные состояния КА
- 25. Кванты времени и пространства
- 26. Геометрия поля и шаблона окрестности КА Шаблон
- 27. Состояние ячейки Часть переменных относится к ионно-пролетной
- 28. Классификация «столкновений» в ионно-пролетной модели. Правила первого
- 29. Второй полуход: правила перехода
- 30. IV. КА-модель ионной имплантации: параметризация и результаты
- 31. Расчет вероятностей Связь углов рассеяния θ
- 32. Расчет потерь энергии При отсутствии «столкновений» потери
- 33. Все зависимости рассчитаны для эталонного случая Si:P.
- 34. Фрагмент поля КА, показывающий распределение заторможенных ионов.
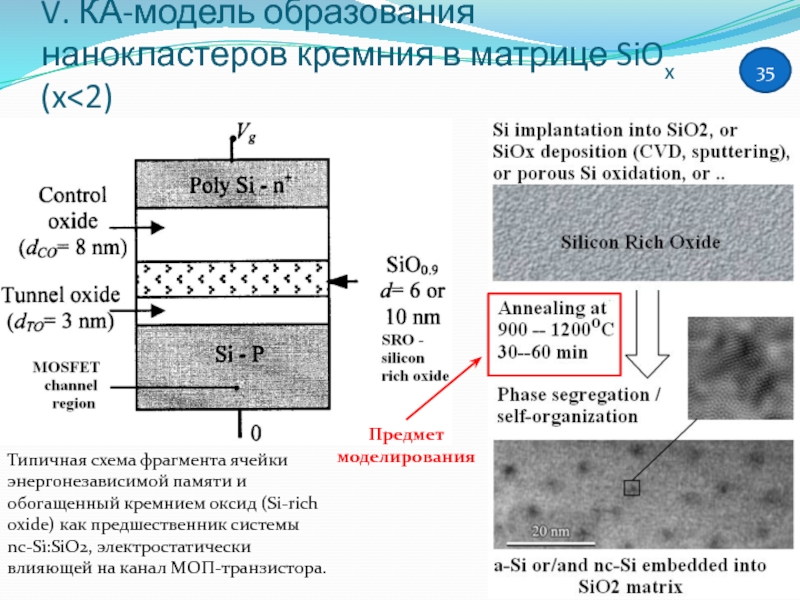
- 35. V. КА-модель образования нанокластеров кремния в матрице SiOx (x
- 36. Нами принято значение ρ=2.23 г/см3 для плотности
- 37. Физические константы Состояние ячейки Оценка «энергии ячейки»
- 38. Модельная зависимость U(x,y) с двумя областями
- 39. Оценка вероятностей, сходная с выражением Ферми-Дирака Правила
- 40. Алгоритм поиска кластеров Схема использованного нами
- 41. Рис. 4. Эволюция δ-образа поперечного сечения
- 42. At y/x=1.1 ratio and T=11500C [1]
- 43. VI. Заключительные замечания КА-моделирование особенно плодотворно в
Слайд 1Применение клеточных автоматов в математическом моделировании технологии микро- и наноэлектроники
Часть II:
Слайд 2Содержание
Предварительные замечания
Семантика клеточных автоматов (КА) на гексагональной сетке
КА-модель ионной имплантации: концептуальный
КА-модель ионной имплантации: параметризация и результаты
КА-модель образования нанокластеров кремния в матрице SiOx (x<2)
Заключительные замечания
2
Слайд 3I. Предварительные замечания
В России наибольший опыт КА-моделирования накоплен в новосибирской школе
О. Л. Бандман, “Метод построения клеточно-автоматных моделей процессов формирования устойчивых структур”, ПДМ, 2010, № 4, 91–99 - http://mi.mathnet.ru/pdm248 О.Л. Бандман, “Отображение физических процессов на их клеточно-автоматные модели”, Вестник Томского государственного университета. Управление, вычислительная техника и информатика, 2008. №2. С. 5-17
Задача моделирования какого-либо естественного или лабораторного процесса ставится обычно следующим образом. Известны следующие величины: 1) размеры области, в которой происходит моделируемый процесс, 2) свойства среды, в которой он происходит, 3) начальные и краевые условия, 4) внешние воздействия. Главный результат моделирования – это скалярная u(x,t) или векторная u(x,t) функция, представляющая пространственную динамику изучаемого процесса (распределение концентраций веществ, участвующих в процессе, интенсивность магнитного или электрического поля, поле скорости потока и т.д.).
КА модель должна быть справедливой для всей области значений моделируемых величин.
Размеры КА-модели должны быть такими, чтобы она была реализуема на имеющемся оборудовании в приемлемое время.
Следует правильно выбрать множество базовых параметров КА-модели, для которых масштаб (отношение физических значений к модельным) вычисляется явно, так как оба значения известны. Обычно, ими являются инварианты моделируемого явления, такие как безразмерный коэффициент диффузии, коэффициент Рейнольдса, скорость реакции и др.
В численных методах математической физики масштабирующие коэффициенты выбираются только для шага по времени (τ), и шага по пространству (t). Все остальные величины иногда нормализуются, но не подвергаются преобразованиям.
3
Слайд 4Поскольку все величины дискретны, масштабы должны быть определены для всех значений,
Опыт применения КА-моделирования еще не достаточно богат, чтобы считать некоторые масштабы достаточно достоверными и проверенными на практических задачах или в натурных экспериментах.
КА-модели разнообразны, большинство из них существенно нелинейны с совершенно непредсказуемым поведением, присущим так называемым «сложным» систем; поэтому можно говорить об искусстве конструирования КА-моделей
Схема работы асинхронного КА:
а) на поле случайным равновероятным образом определяются координаты некоторой i–й клетки с вектор-состоянием ci; б) случайным равновероятным образом определяется соседняя с ней клетка – ck; в) две выбранные соседние клетки взаимодействуют между собой по формулам вида
где функции F1 и F2 определяются физическим уравнением и, как правило, должны обеспечивать закон сохранения вещества.
В качестве синхронного КА, описывающего двумерную диффузию, можно привести КА Ооно-Кохомото с шаблоном Неймана (t- дискретное время, (i,j) – индекс ячейки, M>0):
Синхронные модели ближе определению КА, легче распараллеливаются, однако более чувствительны к эффектам дискретизации/накопления и жесткие в отношении законам сохранения
4
Слайд 5В.К. Ванаг Исследование пространственно распределённых динамических систем методами вероятностного клеточного автомата // Успехи
Вероятностные КА
КА, в которых состояния ячеек в последующий момент времени определяются на основе некоторых вероятностей, называются вероятностными КА (ВКА). В классических ВКА правила переходов имеют абстрактный характер и не связаны однозначно с реальными процессами, происходящими в моделируемой системе. В таких автоматах при моделировании процесса для каждой ячейки датчиком случайных чисел генерируется случайное число Q (0 < Q < 1), которое сравнивается с вероятностью w реализации этого процесса. Если Q < w, то процесс реализуется. К таким КА относятся метод реакционного решеточного газа, метод прямого стимулирования Монте-Карло и метод вероятностного КА с применение процедуры Монте-Карло. В ВКА вместо функции F необходимо задать набор вероятностей изменения состояния клетки, которые показывают, какой будет вероятность перехода i-го элемента из состояния в n-й момент времени в состояние в последующий (n+1)-й момент времени при условии, что состояния его ближайших соседей в n-й момент времени принимали определенные значения.
Для решения наиболее трудных задач типа "реакция – диффузия – конвекция" с учетом флуктуаций был разработан метод вероятностного клеточного автомата с применением процедуры Монте-Карло (ВКА-МК или просто ВКА). Клеточный автомат представляет собой регулярную решетку, состоящую из элементарных ячеек. Форма решетки может быть не только квадратной, но и прямоугольной с сильно вытянутыми ячейками. Каждая ячейка характеризуется набором целых чисел: числом молекул соответствующего сорта в данной ячейке (например, nA, nB, nC в случае трех сортов молекул A, B и C) и своими целочисленными координатами (например, i и j). Ячейке приписывается также определенный объем V и линейный размер l=(V)^1/3. Объем V используется при задании вероятностей протекания химических реакций в ячейках.
5
Слайд 6массив клеток разбит на множество конечных, отдельных однородных частей-блоков
дается правило для
одно и тоже правило применяется ко всем блокам.
блоки не перекрываются и нет обмена информацией между соседними блоками
разбиение меняют от шага к шагу так, чтобы было некоторое перекрытие блоков, используемых на соседних шагах
каждый из блоков синхронно поворачивается на случайный (для одного блока) угол ±π/2
Блочно-поворотный механизм Марголуса
В практике моделирования физических процессов происходит отход от определения классического КА в традиции фон Неймана – Лейбница, а общая стратегия приближается к традиции Цузе.
Главная особенность клеточно-автоматного моделирования состоит в том, что обычные непрерывные уравнения физики нуждаются в нетривиальной, как правило, интерпретации, чтобы им была придана математическая форма КА.
Если не рассматривать квантовые КА-модели, где состояние ячейки КА непосредственно связано с волновой Ψ-функцией, то чрезмерное уменьшение размера ячейки и стремление к детализации лишь ухудшает эффективность от использования КА-подхода
6
Слайд 7II. Семантика КА на гексагональной сетке
Специфика нашего подхода состоит не в
Мы будем давать потенциальную физико-химическую интерпретацию поведения КА, подразумевая, что решается какая-либо из задач химической кинетики реакций на поверхности либо тонкой пленки, либо на внутренней поверхности мезопористого материала. Такие задачи, связанные, например, с самоорганизацией адатомов на поверхности, характерны для нанотехнологии.
Гексагональные сетки (ГС) необходимо использовать для процессов, в которых важна изотропность, например, в задачах гидродинамики, газодинамики и диффузии. Поведение КА на ГС изучено слабо (по сравнению с квадратными сетками).
Реконфигурируемые шаблоны для клеточного автомата на ГС: а – двухтактный; б – трехтактный
7
Слайд 8Снежинкоподобные формы роста кристалла в растворе хлорида аммония разные моменты времени
Абашева Э.Р. Исследование и моделирование процессов кристаллизации с применением клеточных автоматов (2007)
Полимероподобные глайдеры с периодом 2. Движение цепочки слева направо (показаны 2 последовательных хода/состояния). Правила перехода задаются kcode = 0022000220022001122200021210
Каждая клетка может находиться в 3-х состояниях, различающихся по цвету (2-чёрная клетка, 1-красная, 0- точка). Wuensche A. Glider dynamics in 3-value hexagonal cellular automata: the beehive rule (2005)
8
II.A. КА с гексагональной сеткой на плоскости
С помощью таких паттернов, на наш взгляд, можно моделировать термически активированное движение атомных ступенек вещества по поверхности твердого тела (А.Л.Асеев, А.В.Латышев. Электронная и ионная литография: наноструктурирование , 2012)или дать семантическую интерпретацию движения олигомерных пептидов при электрофорезе.
Слайд 9Таблица. Правила перехода, задаваемых kcode = 0022000220022001122200021210.
КА Фредкина (0 и 1)
КА называется тоталистичным, если его локальная функция перехода зависит только от суммы состояний соседей и, быть может, состояния центральной ячейки. Тогда локальная функция перехода легко шифруется числом kcode.
Для КА размерности (v, k), где v –число состояний, k – количество соседей одной клетки, длина kcode переходов.
Для КА (3,6) общее число тоталистичных КА равно 36=729, а длина L=28. Идея kcode наследована от записи правил Вольфрама, если считать kcode записью числа в v-ричной системе.
9
Слайд 10«Игровые» КА обычно разыгрываются на бесконечной доске, но моделирующие наноразмерные процессы
Рассмотрим битовый КА Фредкина на ГС и с начальной конфигурации в 1 живую клетку. На рис. представлены два варианта развития КА на ГС 20×20 для случая изолированного и замкнутого циклически поля при одинаковых начальных условиях. При замыкании наблюдается характерная для КА Фредкина репликация, причём размер ГС был 2m×2m (m>1), а начальные условия допускали вариабельность.
10
Слайд 11Симметричные изомероподобные паттерны в ГС-аналоге КА Конвэя. Можно увидеть, что происходит
Несимметричные изомероподобные паттерны (одной фигуры в динамике) в ГС-аналоге КА Конвэя.
Для удобства введем некоторое обозначение. Пусть запись [a,b] для КА на ГС, по типу игры Конвэя, обозначает следующее правило:
клетка, при сумме состояний её шести соседей, меньшей a и большей b, переходит в состояние 0 (“умирает”); при сумме, равной a или b≥a, переходит в состояние 1 (“рождается”); в остальных случаях не меняет состояние. КА работает по правилу [3,4]. В таком семействе автоматов интересны правила [2,2], [2,3], [3,3…6], т.к. здесь можно наблюдать устойчивые паттерны.
Рисунки/расчеты на этом и последующих слайдах выполнены средствами оригинальной программы SoftCAM.
Матюшкин И.В., Хамухин А.В. Применение языка UML при проектировании клеточных автоматов // Известия ВУЗов. Электроника, №6, 2010, с.39-48.
Для некоторых тоталистичных КА на ГС с двумя состояниями были обнаружены устойчивые унарно- и/или бинарно-периодические структуры – агломераты, состоящие из чередований в близком к шахматному порядку ячеек 0-го и 1-го состояния. Возможная семантическая интерпретация: хаотический поток жидкости течет по поверхности между химически инертными островками, огибая их.
Пример: kcode = 0111100. Примерные границы одного из агломератов выделены зеленой линией.
11
Слайд 12
0101002002210000101122201000;
1200122011001110101120001000;
0010122201010210211120001000;
1201010010210122110120001000;
0102222210111010210120001000;
2221010222010101000120101000;
2110122210011011000120001000;
2121211100222101000121101000;
1222010021201210201120001000;
Слева: Разнообразие глайдеров в КА на ГС, задаваемого kcode = kbase=2200122221211110101122001000.
Глайдер-пожиратель (a – до столкновения, б – после него) и паттерн, копирующий сам себя. kcode=kbase минус 1 в позиции 11
При встрече глайдеров, т.е. прямолинейно движущихся паттернов, друг с другом могут происходить: аннигиляция (взаимное уничтожение при столкновении), отсутствие взаимодействия (продолжение движения после столкновения) или несохранение импульса (изменение направления движения).
Ниже некоторые правила наряду с kbase, порождающие глайдеры:
12
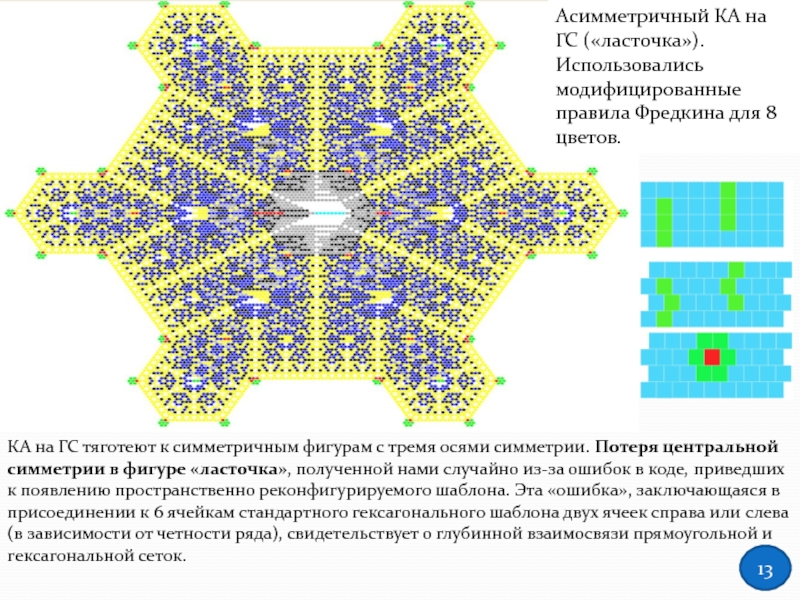
Слайд 13КА на ГС тяготеют к симметричным фигурам с тремя осями симметрии.
Асимметричный КА на ГС («ласточка»). Использовались модифицированные правила Фредкина для 8 цветов.
13
Слайд 14Интерес к КА модели на сфере обусловлен потребностями моделирования физико-химических процессов
Первый способ заключается в линейном распределении сферических углов, второй - основан на модели “электронного взаимодействия”, когда для каждой точки, случайно брошенной на сферу, рассчитывается действие силы со стороны всех других по закону обратных квадратов. Далее происходит самоорганизация точек к некоторому устойчивому положению. Задавая погрешность, можно получить искомый результат (средствами MATLAB, www.mathworks.com/matlabcentral/newsreader/view_thread/21083), но этот способ ресурсоёмкий при большом количестве точек на сфере. При построении первым способом на полюсах образуются некоторые локальные дефекты, нежелательные сгущения узлов, что неприемлемо для КА-моделирования. Второй метод даёт более наглядную картину, но не гарантируется отсутствие неоднородности и правильность форм ячеек.
Из теоремы Эйлера для выпуклых многогранников следует, что невозможно построить однородную ГС на сфере. Однако если допустить два типа ячеек КА, то можно приблизиться к этому.
14
II.В. КА на сфере.
Кац Е.А. Леонард Эйлер и … // «Энергия: экономика, техника, экология», 2004
Слайд 1515
Стратегия масштабирования икосаэдрической треугольной сетки (показаны три уровня масштаба)
Наиболее популярные в
Сетка «широта-долгота» -непригодность из-за сгущения линий у полюсов
1) икосаэдрическая треугольная (известна с 1968г); 2) икосаэдрическая гексагональная (двойственна к предыдущей);
3) кубированная (« cubed sphere », линии сетки на кубе проецируются на сферу);
4) Инь-Ян (предложена в 2004г Кагеямой, перекрытие двух фрагментов составляет 6% площади сферы).
Икосаэдр лучше всего из всех правильных многогранников подходит для триангуляции сферы методом рекурсивного разбиения, поскольку искажение получающихся треугольников по отношению к правильным минимально.
Основные требования к сеткам:
Отсутствие дефектов сетки (сгущение на полюсах, кривизна ячеек)
Равномерность
Простота определения шаблона окрестности
Высокая однородность сетки
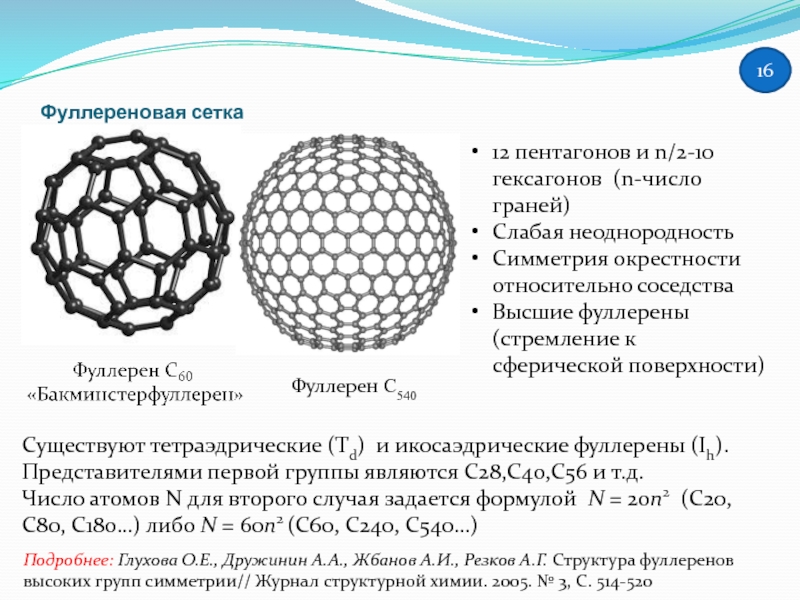
Слайд 16Фуллереновая сетка
Существуют тетраэдрические (Td) и икосаэдрические фуллерены (Ih).
Представителями первой группы являются
Число атомов N для второго случая задается формулой N = 20n2 (С20, С80, С180…) либо N = 60n2 (С60, С240, С540…)
16
Фуллерен С540
12 пентагонов и n/2-10 гексагонов (n-число граней)
Слабая неоднородность
Симметрия окрестности относительно соседства
Высшие фуллерены (стремление к сферической поверхности)
Подробнее: Глухова О.Е., Дружинин А.А., Жбанов А.И., Резков А.Г. Структура фуллеренов высоких групп симметрии// Журнал структурной химии. 2005. № 3, С. 514-520
Слайд 1717
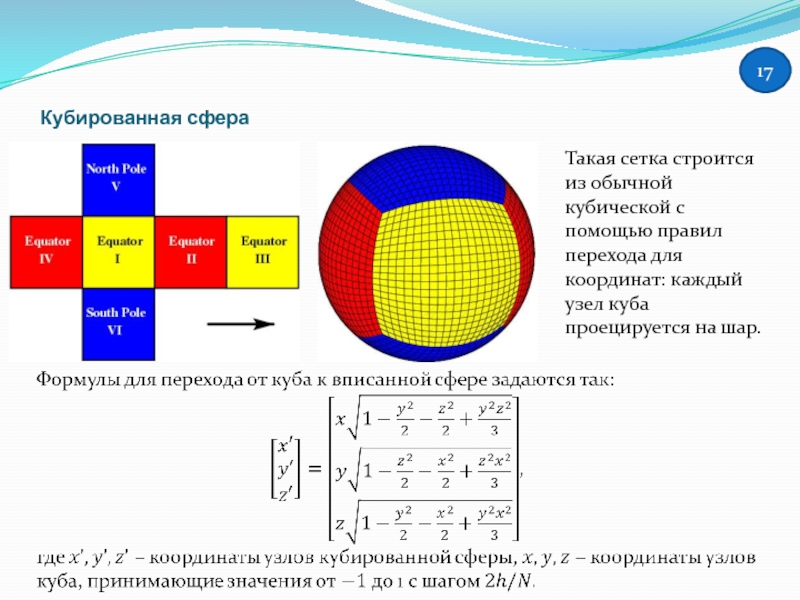
Кубированная сфера
Такая сетка строится из обычной кубической с помощью правил перехода
Слайд 18Модель гетерофазной бимолекулярной реакции
Реакция A+B→AB→С на поверхности поры.
18
Абстрактная модель
Изначально содержится небольшое депо реагентов А и B
Пять состояний ячейки: {0,A,B,A+B,C}
Асинхронно-парный режим
Процессы адсорбции /десорбции
Правила перехода являются парными и задаются с помощью таблицы вероятностей. Возможность задавать различные вероятности (и сценарии вероятностей) придаёт гибкость и общность нашей модели.
Можно описывать не только реакцию на поверхности поры, но и реакцию на внешней поверхности сферической глобулы. Такая реакция, например, относится к самоорганизации аминокислот или нуклеиновых оснований на поверхности искусственной наночастицы, внедренной в организм человека.
Слайд 19
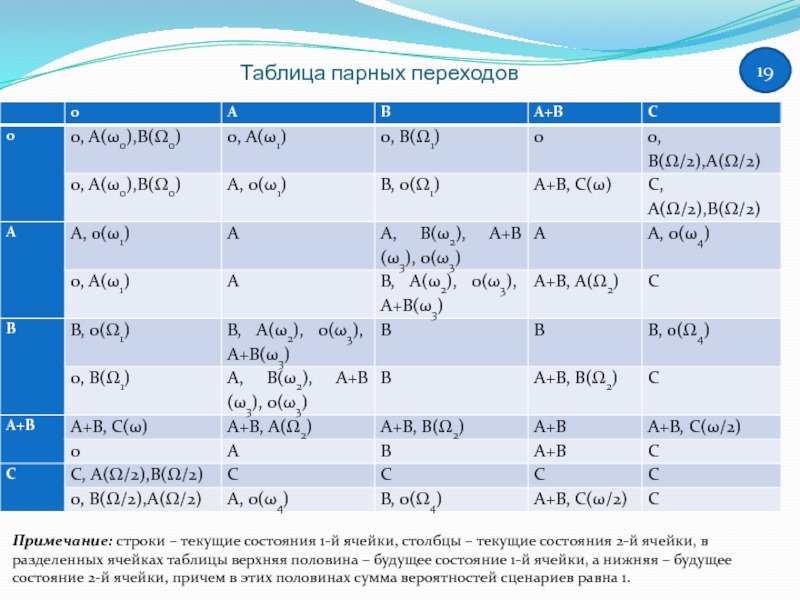
Таблица парных переходов
19
Примечание: строки – текущие состояния 1-й ячейки, столбцы –
Слайд 20
Области реагента А в реагенте В, полушария кубированной сферы. На
Схема парного механизма симуляции:
Поле КА пробегается за 1 глобальный ход последовательно, в случайном порядке
Центральная и случайно выбранная ячейка взаимодействуют попарно (см. пред.слайд)
Если на глобальном ходу обе ячейки взаимодействовали, то возможен запрет на применение правил перехода
В таблице переходов потенциально можно учесть влияние заштрихованных ячеек общей окрестности
20
Слайд 21
КА на фуллерене С60 на 0, 50 и 220 ходах. w=
Фуллерен С540 давал схожую картину: независимо от вероятностей адсорбции, в конце наблюдалось полное заполнение одним из реагентов (возможно, за исключением подвижной точки); при почти равных вероятностях адсорбции – эффект триггерности, когда поле КА заполнялось либо зеленым, либо фиолетовым цветом. При увеличении вероятностей, отвечающих за стабильность (малая десорбция) вещества С, динамика переходит в хаос и островкого роста не наблюдается.
21
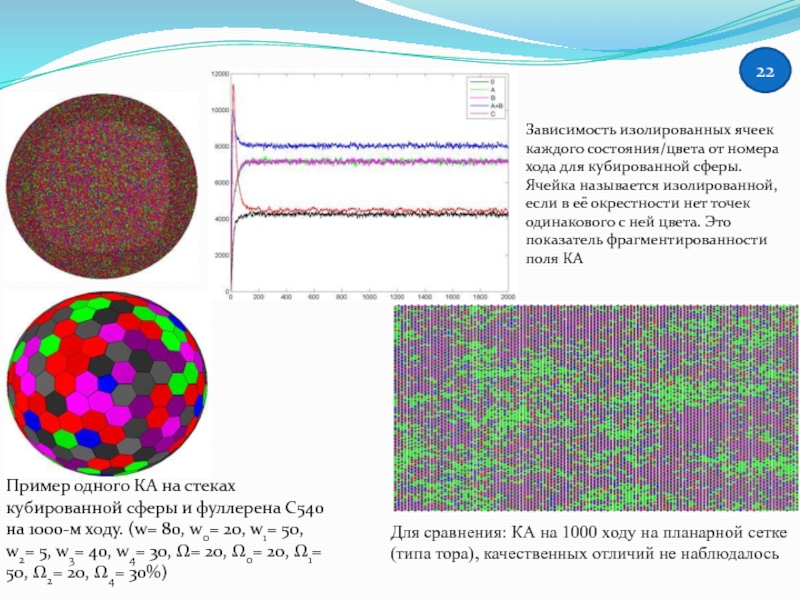
Слайд 22Зависимость изолированных ячеек каждого состояния/цвета от номера хода для кубированной сферы.
Пример одного КА на стеках кубированной сферы и фуллерена С540 на 1000-м ходу. (w= 80, w0= 20, w1= 50, w2= 5, w3= 40, w4= 30, Ω= 20, Ω0= 20, Ω1= 50, Ω2= 20, Ω4= 30%)
Для сравнения: КА на 1000 ходу на планарной сетке (типа тора), качественных отличий не наблюдалось
22
Слайд 23III. КА-модель ионной имплантации: концептуальный анализ и формализация
Метод ионной имплантации (ИИ)
Задача о накоплении дефектов и аморфизации при ИИ традиционно решалась методами дифференциальных уравнений или молекулярной динамики (ММД). Первые из них не учитывают стохастическую природу процессов, а вторые требуют слишком больших компьютерных ресурсов при попытке проследить всю эволюцию материала при облучении. Поэтому с помощью ММД обычно прослеживают состояние вещества лишь на первой стадии – после попадания единичных ионов, либо после последовательного попадания ионов в одну и ту же ячейку, но без учета промежуточных процессов между ними, в частности, взаимодействия каскадов смещений атомов в процессе облучения.
23
Слайд 24Алгоритм общей модели
Разделив переменные состояния КА на «быстрые» и «медленные», можно
Задание начальных значений всех переменных поля КА;
Запуск М итераций КА для «быстрых» переменных (ионно-пролетная модель);
Задание начальных случайных возбуждений граничных ячеек;
Первый полуход: актуализация вероятностей разных переходов;
Второй полуход: модификация «быстрых» переменных;
Переход к следующей итерации (до М-й);
Модификация «медленных» переменных на основе значений части «быстрых» переменных
Применение локальных функций перехода для «медленных» переменных (модель вторичного дефектообразования )
Переход к п.2. или завершение КА-расчета
КА-модели можно рассматривать как промежуточные между макроскопическими, записываемыми дифференциальными уравнениями, и атомистическими моделями дефектообразования.
Преимущества КА-подхода заключаются в принципиальной возможности имитации на обычном компьютере эволюции слоя вещества, подвергаемого ИИ.
Этот этап призван продемонстрировать возможности КА-подхода в задачах ИИ, но он не претендует на замену хорошо зарекомендовавших себя программ TRIM, SRIM, TRIDYN и пр.
Метод Монте-Карло (МК), используемый в классических программах моделирования ИИ, дает избыточную информацию для моделей вторичного дефектообразования. КА-модели представляют более высокий уровень абстракции, не рассматривая детали единичного столкновения иона с веществом мишени.
24
Слайд 25Кванты времени и пространства
Ионный поток j уместно связать с вероятностью ρ
Для 3D-случая. В случае 2D
Эталонный случай – ИИ для Si и ионов Р+ с энергией ~100 кэВ):
T1=10-14÷10-15c – время пролета иона дистанции, равной размеру ячейки Lz;
T2= 10-12–10-11с – время релаксации энергии в т.н. spike-моделях;
T3=10-2c – наименьшее из характерных времен, описывающих кинетику точечных дефектов при комнатной температуре
За общее время хода медленной модели (T=T3) на поле 2D-КА будет попадать менее 10 частиц (примем N=100 и ρ=10%), поэтому условно квант времени ионно-пролетной модели равен 0.01-0.1 T3
И.В. Матюшкин, С.В. Коробов, Н.А. Зайцев, И.А. Хомяков, С.Н. Орлов (НИИМЭ), А.Н. Михайлов, Д.В. Гусейнов (ННГУ). Клеточно-автоматный подход к моделированию дефектообразования при ионной имплантации // Материалы IV Всероссийской конференции «Физические и физико–химические основы ионной имплантации», Новосибирск, 23-26 октября 2012 года, с.49 –источник цитирования
25
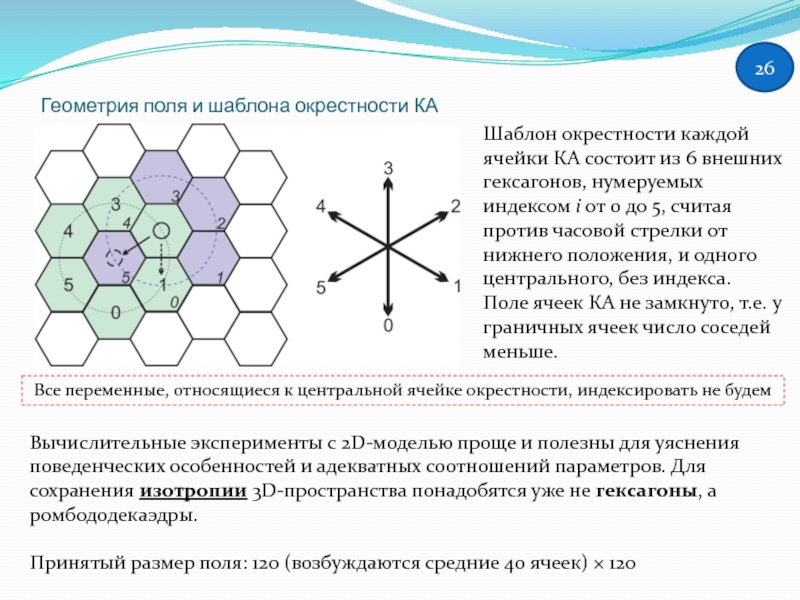
Слайд 26Геометрия поля и шаблона окрестности КА
Шаблон окрестности каждой ячейки КА состоит
Все переменные, относящиеся к центральной ячейке окрестности, индексировать не будем
Вычислительные эксперименты с 2D-моделью проще и полезны для уяснения поведенческих особенностей и адекватных соотношений параметров. Для сохранения изотропии 3D-пространства понадобятся уже не гексагоны, а ромбододекаэдры.
Принятый размер поля: 120 (возбуждаются средние 40 ячеек) × 120
26
Слайд 27Состояние ячейки
Часть переменных относится к ионно-пролетной подмодели, другая – к процессам
- направление скорости иона
– дискретные уровни энергии иона
– уровни локального возбуждения
- (направление) скорости передачи возбуждения
- количество прекративших движение ионов в ячейке (обычно не более 5-10)
- код операции
Переменная медленной подмодели
В случае маловероятных двойных, тройных и т.д. нахождений/прихода ионов в одну и ту же ячейку вся энергия передается одному иону, а остальные переходят в состояние покоя. Значение E=0 служит маркером отсутствия движущегося иона в ячейке
27
Слайд 28Классификация «столкновений» в ионно-пролетной модели. Правила первого полухода.
В контексте КА «столкновение»
Отсутствие «столкновения» означает скользящие столкновения иона с атомами мишени, не приводящие к смещениям атомов, и слабо искажающие траекторию его движения. «Слабые столкновения» приводят к искажению траектории на больший угол (условно от 50 до 600) и смещению/переносу иона в соседнюю ячейку при сохранении V. «Сильные столкновения» приводят к результирующему углу рассеяния более 600 и смене направления V на ± 1
Случай op=0 означает также перевод иона в разряд покоящихся, р:=p+1
Случайная величина ξ разыгрывается для каждой ячейки на каждом ходу
28
Слайд 29Второй полуход: правила перехода
Множество индексов I2 отражает сильные «столкновения» с вероятностью
Энергия локального возбуждения ε генерируется за счет ударной передачи кинетической энергии атомам ячейки (появление атомов отдачи в результате соударений с ионом или другим атомом отдачи, в том числе из другой ячейки) и за счет фононного возбуждения.
Введенные множества
Правила перехода по заторможенным ионам и скорости
Правила перехода по энергии иона
Правила перехода по энергии локального возмущения, дефиниции коэффициентов
29
Слайд 30IV. КА-модель ионной имплантации: параметризация и результаты
Параметризация КА-модели должна опираться на
Для ионно-пролетного 2D КА критичное значение имеет выбор значений двух вероятностей (ω и Ω) и трех энергетических параметров α, β и γ, формализующих потери ионом энергии при «сильных», «слабых» и «отсутствии» «столкновений». Все эти коэффициенты зависят от текущей энергии иона E.
Если прицельный параметр P столкновения считать равномерно распределенной величиной (в предположении аморфной мишени с плотностью атомов n на единицу площади), то угол ϕ будет иметь неравномерное распределение, и при этом в силу монотонности зависимости ϕ(P) можно записать для вероятности
В качестве эталона рассматриваем ИИ фосфора в кремний с энергией 100кэВ
30
Слайд 31Расчет вероятностей
Связь углов рассеяния θ (в системе ц.м.) и ϕ (в
Три случая:
Из приближенной аппроксимации таблицы степенной зависимостью:
W(60,180)=0.22*E-0.58/ Pmax
W(5, 60)= ( 1.16*E-0.4 – 0.22*E-0.58) / Pmax
W (0, 5)= 1-1.16*E-0.4/ Pmax
Излагаемая параметризация основана на формулах, приведенных в документации SRIM. J.F. Ziegler, J.P. Biersack, M.D. Ziegler. The Stopping and Range of Ions in Matter, Ion Implantation Press, 2008, 398 p.
31
Слайд 32Расчет потерь энергии
При отсутствии «столкновений» потери энергии (параметр γ) происходят за
Непрерывные потери
Дискретные потери
Примечание:
Значения вероятностей в таблице не нормированы.
32
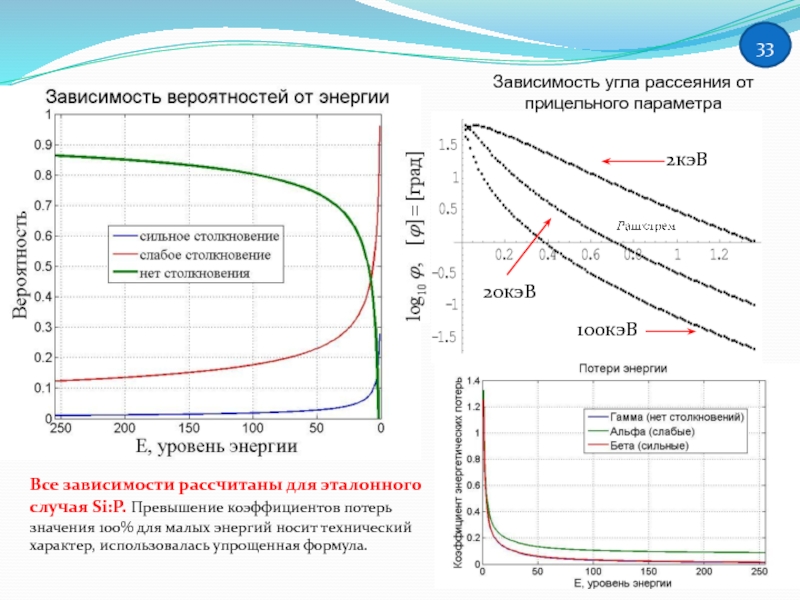
Слайд 33Все зависимости рассчитаны для эталонного случая Si:P. Превышение коэффициентов потерь значения
33
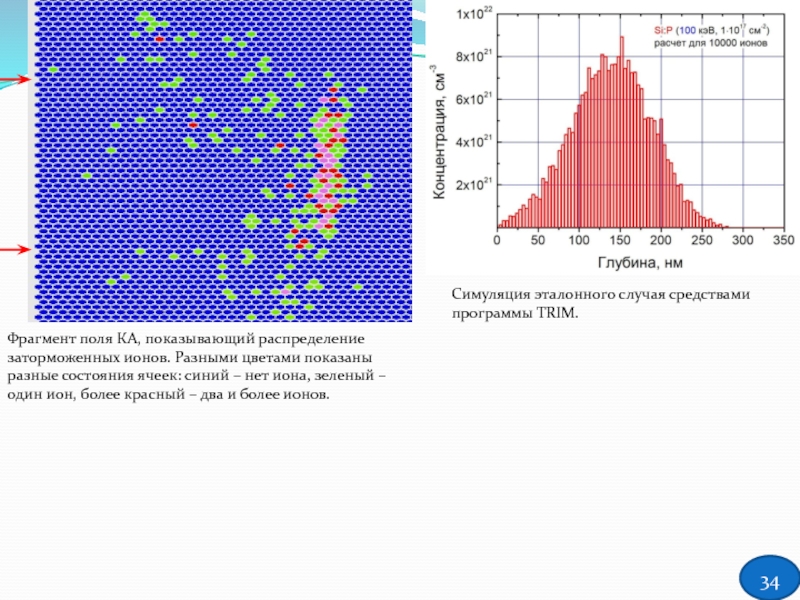
Слайд 34Фрагмент поля КА, показывающий распределение заторможенных ионов. Разными цветами показаны разные
Симуляция эталонного случая средствами программы TRIM.
34
Слайд 35V. КА-модель образования нанокластеров кремния в матрице SiOx (x
Предмет моделирования
35
Слайд 36Нами принято значение ρ=2.23 г/см3 для плотности вещества в SiO2-ячейке. Количество
Ячейка кремния содержит не более 8 атомов. Изменение объема при полной сепарации не превышает по модулю 7.5%.
При полном разделении фаз
В отличие от известных КА-моделей диффузии, хотя и имеющая общее основание с моделью Ооно-Кохомото, развиваемая нами КА-модель является синхронной по времени, гомогенной по 3D-пространству, не использует блочно-поворотность и является детерминированной, несмотря на введение вероятностей. Первая и третья особенности заставляют нас уделить внимание выполнению закона сохранения вещества при формулировке парных взаимодействий в уравнениях локального перехода. Мы отказались от использования блочно-поворотности ввиду сильной гетерогенности среды, где проходит диффузия.
Сетка принята кубической (26 соседей), но для учета неравноценности их расположения при расчете переходов атомов введены весовые коэффициенты ai; для угловых ячеек вес, очевидно, меньше; сумма весов равна 1 для всех ячеек, кроме граничных, где она меньше 1 (чтобы сохранить взаимность потоков и удовлетворить закону сохранения вещества).
36
Слайд 37Физические константы
Состояние ячейки
Оценка «энергии ячейки»
Центральным понятием нашей КА-модели является «энергия ячейки»
37
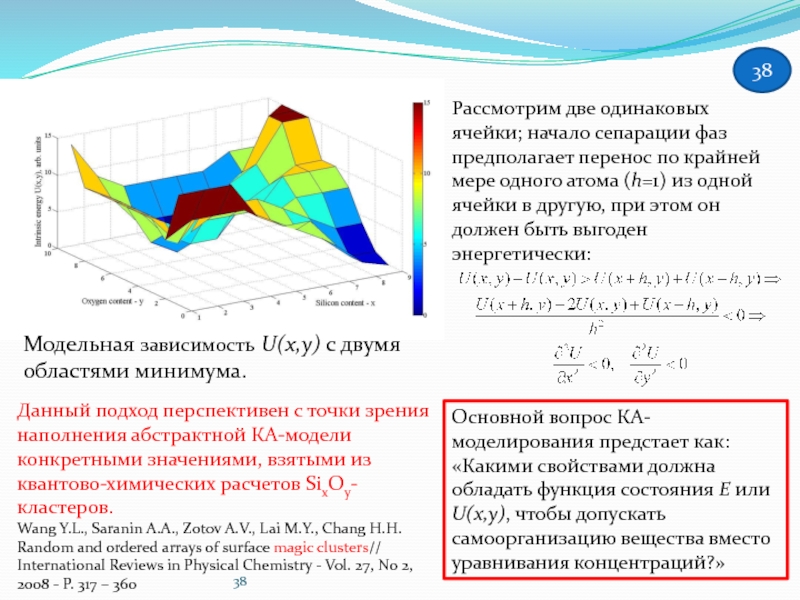
Слайд 38
Модельная зависимость U(x,y) с двумя областями минимума.
Рассмотрим две одинаковых ячейки; начало
Данный подход перспективен с точки зрения наполнения абстрактной КА-модели конкретными значениями, взятыми из квантово-химических расчетов SixOy-кластеров.
Wang Y.L., Saranin A.A., Zotov A.V., Lai M.Y., Chang H.H. Random and ordered arrays of surface magic clusters// International Reviews in Physical Chemistry - Vol. 27, No 2, 2008 - P. 317 – 360
Основной вопрос КА-моделирования предстает как:
«Какими свойствами должна обладать функция состояния E или U(x,y), чтобы допускать самоорганизацию вещества вместо уравнивания концентраций?»
38
Слайд 39Оценка вероятностей, сходная с выражением Ферми-Дирака
Правила локального перехода
Особо следует отметить, что
39
Слайд 40Алгоритм поиска кластеров
Схема использованного нами алгоритма, предполагающего только один цикл прохода
Каждой клетке ставится в соответствие номер кластера, и он вначале обнуляется для всех ячеек, а также вводится переменная «число кластеров» (cluster count - CC) и приравнивается 0;
В смежных клетках, включая текущую по циклу, ищется минимальный номер кластера (за исключением нулевого номера) при условии, что параметр состояния δ текущей и смежной клетки одинаков; затем переходим шагу 4;
Если, при выполнении условия а), номер кластера при шаге 2 не был найден, то создается список ячеек кластера, CC увеличивается на 1, список нумеруется значением СС, текущей клетке присваивается новый номер кластера, равный СС и заносится в созданный список; затем переходим к шагу 6;
Если номер кластера, найденный на шаге 2, оказался равным номеру кластера текущей клетки, то переходим к шагу 6;
В противном случае в список с меньшим номером добавляются все клетки списка клеток с большим номером, после чего список с большим номером удаляется, а клетки с большим номером приобретают меньший номер кластера.
Переход к следующей по циклу клетке и выполнение шага 2.
40
Слайд 41
Рис. 4. Эволюция δ-образа поперечного сечения поля КА от начальной стадии
На начальном этапе симуляции визуально наблюдалась миграция преципитатов кремния и затем их агломерация
41
Слайд 42At y/x=1.1 ratio and T=11500C
[1] B. Garrido Fernandez, M. Lopez, C.
[2] N.E. Maslova et al, Investigation of silicon nanocrystals in silicon suboxide layers by Raman
scattering spectroscopy, Fizika i Tekhnika Poluprovodnikov (in russian). – 2010. -- Vol 44, #8. -- P.1074-1077. http://journals.ioffe.ru/ftp/2010/08/p1074-1077.pdf
Nc-Si average diameter after 1 hour annealing [2]
42
Слайд 43VI. Заключительные замечания
КА-моделирование особенно плодотворно в области технологии микроэлектроники;
На этапе конструирования
Как всегда, сложен вопрос параметризации (не всегда помогает даже изощренная процедура, включающая дорасчетное решение уравнений и обращающая к низкоуровневым моделям/результатам); многие параметры приходится подбирать, что сопряжено с серией долговременных пробных запусков КА-расчета
43































![At y/x=1.1 ratio and T=11500C[1] B. Garrido Fernandez, M. Lopez, C. Garcia, A. Perez-Rodriguez, et](/img/tmb/4/307180/76d2a97a61828ba38a103d1db8a73a1e-800x.jpg)






