- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оригами в помощь геометрии презентация
Содержание
- 1. Оригами в помощь геометрии
- 2. Гипотеза: искусство оригами имеет прямое
- 3. Новизна нашей работы применение
- 4. Для достижения цели и проверки гипотезы
- 6. Оригами в помощь геометрии ОБЪЕКТ
- 7. Практическую значимость исследовательской работы видим:
- 8. Почему мы заинтересовались оригами? В детстве нам
- 9. Слово Оригами в переводе с японского
- 10. История оригами Оригами - это самобытное японское
- 13. В оригаметрии считается: Роль прямых будут
- 14. Аксиомы оригаметрии Аксиома 1. Существует единственный сгиб,
- 15. АКСИОМЫ ОРИГАМЕТРИИ Аксиома 4. Существует
- 16. В 2002 году японский оригамист
- 17. Оригамское решение Теорема 1.Сумма углов треугольника
- 19. Оригамское решение Теорема2. Накрест лежащие углы образованные
- 20. Возьмем лист бумаги с двумя параллельными
- 21. 3) Математическое обоснование
- 22. Из чего состоит любая оригамская
- 23. Задача Прямая, проходящая через середину биссектрисы AD
- 24. Возьмём лист бумаги имеющий форму производного
- 25. Для доказательства параллельности MD и AB
- 26. Теорема Хага
- 28. Частные случаи
- 29. Деление квадрата на три равные части Согнем
- 30. Центральное место геометрии треугольника занимают свойства
- 31. Деление одного из угла квадрата на 3
- 32. Проще всего сложить правильный пятиугольник
- 33. Построение параболы, путем построения семейства касательных
- 37. Спасибо за внимание !
Слайд 1ОРИГАМИ В ПОМОЩЬ ГЕОМЕТРИИ
Выполнили: ученики 8 класса.
ГУО «Хуторская ясли-сад-средняя школа»
Руководитель: Воробей В.В
Слайд 2
Гипотеза: искусство оригами имеет прямое отношение к геометрии.
Цель исследования -
Слайд 4
Для достижения цели и проверки гипотезы нами были решены следующие задачи:
1.Расширить
2.Рассмотреть решение задач и доказательство теорем с помощью оригами.
3.Подобрать материал по использованию оригами на уроках математики, геометрии.
4.Установить связь между математикой и оригами.
5.Сделать выводы о проделанной работе.
Слайд 7
Практическую значимость исследовательской работы видим:
в определении роли оригами в
Слайд 8Почему мы заинтересовались
оригами?
В детстве нам нравилось складывать самолетики, различные фигурки, коробочки
Нам стало интересно, насколько близко связано искусство оригами с математикой?
Слайд 9
Слово Оригами в переводе с японского означает «сложенный из бумаги». В
История возникновения ОРИГАМИ неразрывно связана с изобретением бумаги.
ОРИ -БУМАГА
КАМИ-СЛОЖЕННЫЙ
Слайд 10История оригами
Оригами - это самобытное японское искусство создания моделей различных предметов,
Слайд 13В оригаметрии считается:
Роль прямых будут играть края листа и линии сгибов,
Роль точек – вершины углов листа и точки пересечения линий сгибов друг с другом или с краями листов.
Слайд 14Аксиомы оригаметрии
Аксиома 1. Существует единственный сгиб, проходящий через две данные точки.
Аксиома
Аксиома 3. Существует сгиб, совмещающий две данные прямые.
А В
А
В
а
b
Слайд 15АКСИОМЫ ОРИГАМЕТРИИ
Аксиома 4. Существует единственный сгиб, проходящий через данную точку
Аксиома 5. Существует единственный сгиб, проходящий через данную точку и помещающий другую данную точку на данную прямую.
Аксиома 6. Существует единственный сгиб, помещающий каждую из двух данных точек на одну из двух данных пересекающихся прямых.
a
A
В
А
a
a
A
b
B
Слайд 16
В 2002 году японский оригамист Коширо Хатори обнаружил сгиб,который описал
Аксиома 7. Для двух данных прямых и точки существует линия сгиба, перпендикулярная первой прямой и помещающая данную точку на вторую прямую .
Слайд 17Оригамское решение
Теорема 1.Сумма углов треугольника равна 1800
По аксиоме 4 существует
1
2
3
Слайд 18 Математическое обоснование Получаем, что углы 1, 2 и 3 треугольника совпали при
1
2
3
Слайд 19Оригамское решение
Теорема2. Накрест лежащие углы образованные при пересечении двух параллельных прямых
A
B
1
2
Слайд 20
Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ. Сравним
Согнем лист по секущей АВ. (По аксиоме 1: существует единственный сгиб, проходящий через две данные точки)
Совместим вершины накрест лежащих углов – точки А и В.
Слайд 213) Математическое обоснование
Слайд 22
Из чего состоит любая оригамская задача ?
Из постановки задачи
Из оригамского решения
Из математического обоснования, то есть доказательства того, что в результате действительно получается фигура с требуемыми свойствами
Слайд 23Задача
Прямая, проходящая через середину биссектрисы AD твеугольника ABC и перпендикулярна AD,
A
B
C
D
O
1
M
2
Слайд 24
Возьмём лист бумаги имеющий форму производного треугольника.
Проведём биссектрису AD, согнув лист
A
C
D
B
A
A
C
A
C
D
O
M
B
Слайд 25
Для доказательства параллельности MD и AB сравним углы 1 и 2,
A
B
C
D
O
1
M
2
Слайд 27
Обобщение теоремы
Если совместить правую нижнюю вершину квадрата с серединой верхней стороны, то каждая сторона квадрата делится в определенном отношении, а именно:
правая сторона делится точкой F в отношении 3:5;
левая сторона делится точкой Н в отношении 2:1;
левая сторона делится точкой G в отношении 7:1;
нижняя сторона делится точкой Н в отношении 1:5.
H
G
F
Слайд 29Деление квадрата на три равные части
Согнем бумагу так, чтобы правая нижняя
Слайд 30
Центральное место геометрии треугольника занимают свойства так называемых замечательных точек и
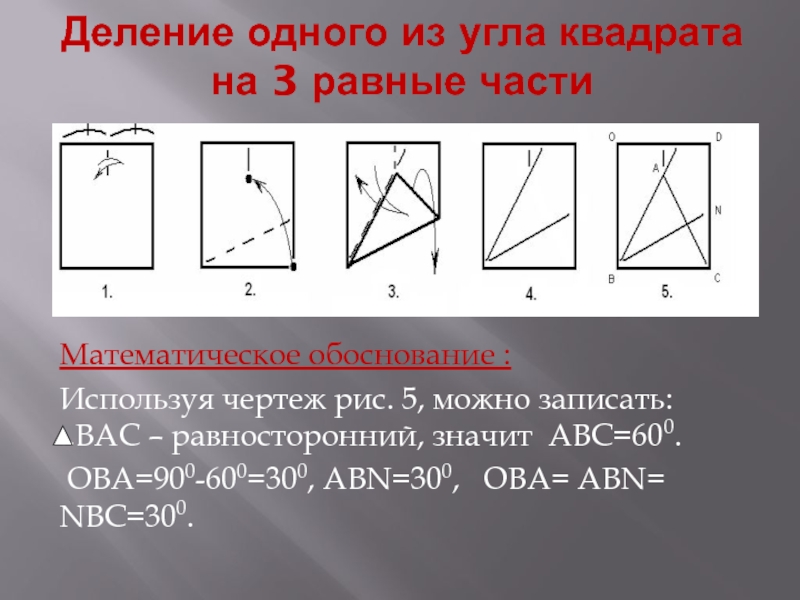
Слайд 31Деление одного из угла квадрата на 3 равные части
Математическое обоснование :
Используя
ОВА=900-600=300, ABN=300, ОВА= ABN= NBC=300.