- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выбор правила голосования. Правило единогласия и правило большинства презентация
Содержание
- 1. Выбор правила голосования. Правило единогласия и правило большинства
- 2. Правило единогласия Правило единогласия – это правило
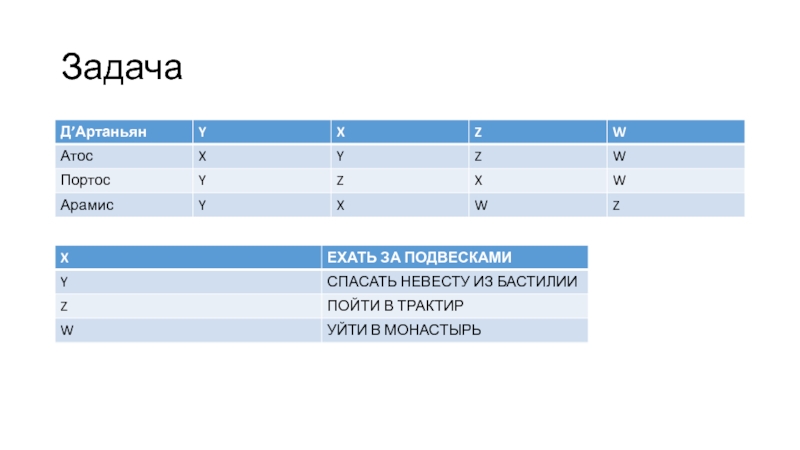
- 3. Задача
- 4. Правило единогласия Плюсы Учитываются предпочтения всех членов
- 5. Референдумы в Швейцарии Может ли возможность проводить
- 6. Правило большинства Плюс использования правила большинства по сравнению с правилом единогласия – снижение издержек.
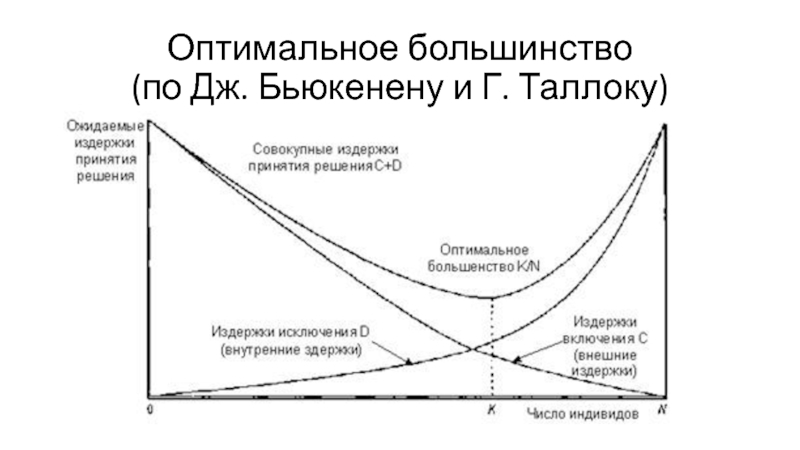
- 7. Оптимальное большинство (по Дж. Бьюкенену и Г. Таллоку)
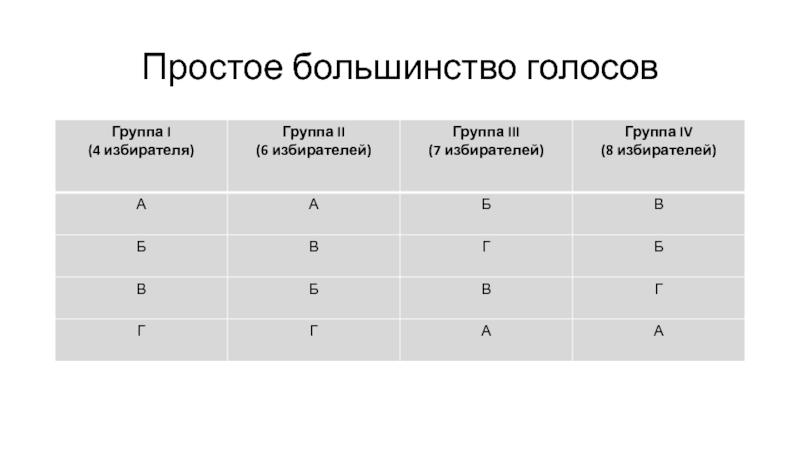
- 8. Простое большинство голосов
- 9. Простое большинство голосов
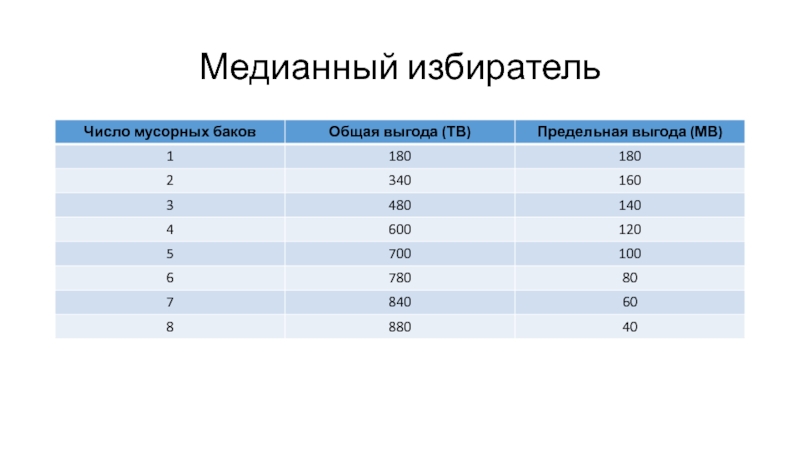
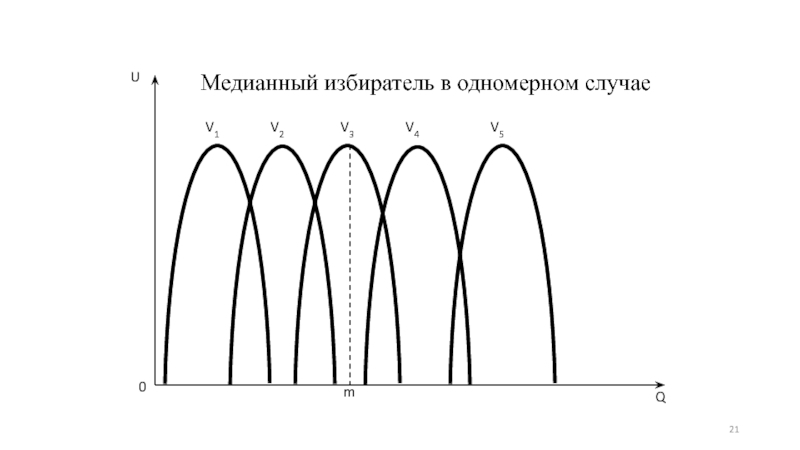
- 10. Медианный избиратель
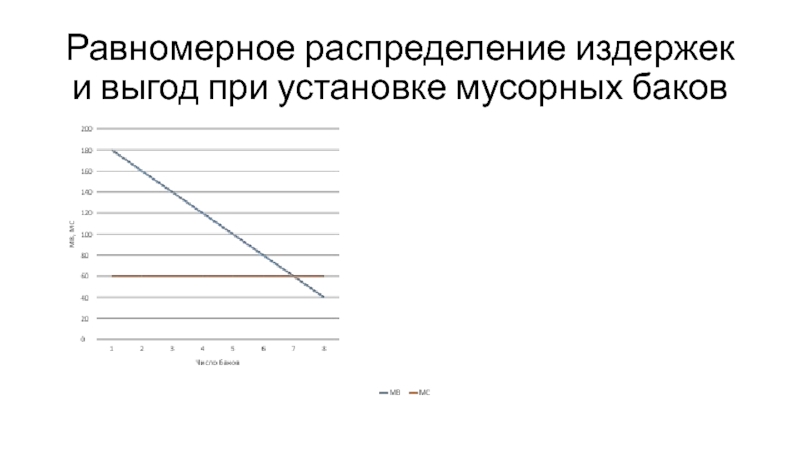
- 11. Равномерное распределение издержек и выгод при установке мусорных баков
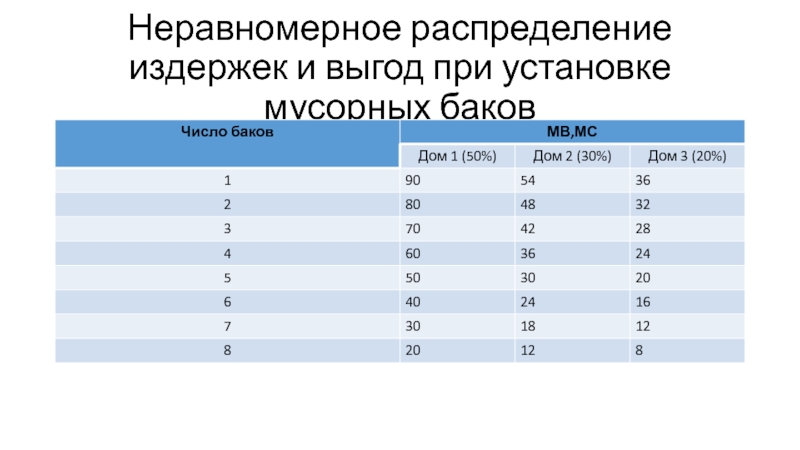
- 12. Неравномерное распределение издержек и выгод при установке мусорных баков
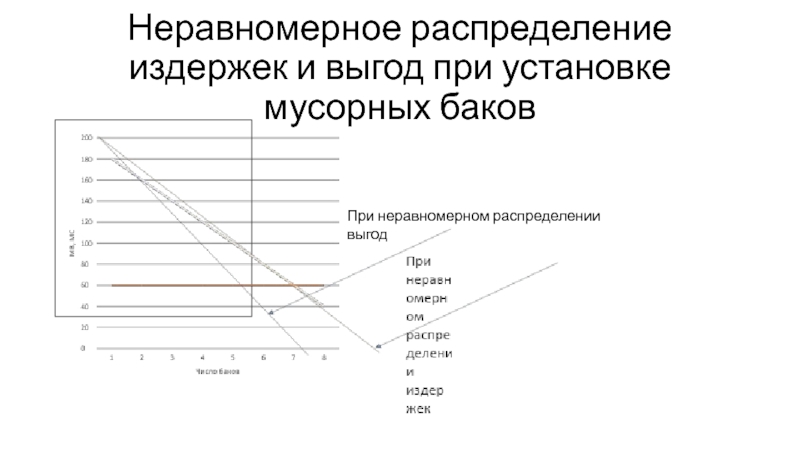
- 13. Неравномерное распределение издержек и выгод при установке мусорных баков При неравномерном распределении выгод
- 14. Теорема Мэя Функция группового принятия решений: Где
- 15. Теорема Мэя
- 16. Теорема Мэя Функция группового выбора есть правило
- 17. Теорема Мэя Нейтральность: Если ранжирование сохраняется для
- 18. Теорема Рэя – Тейлора Если индивид, находясь
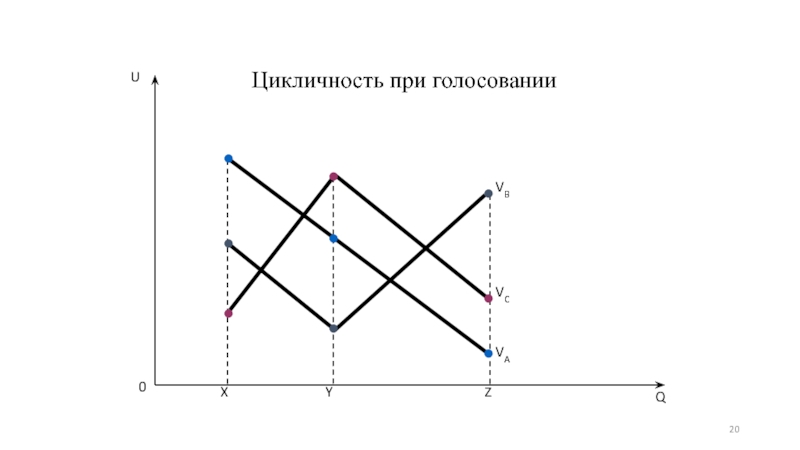
- 19. Парадокс Кондорсе B>C, C>A, A>B
- 20. Цикличность при голосовании 0 Y
- 21. Медианный избиратель в одномерном случае
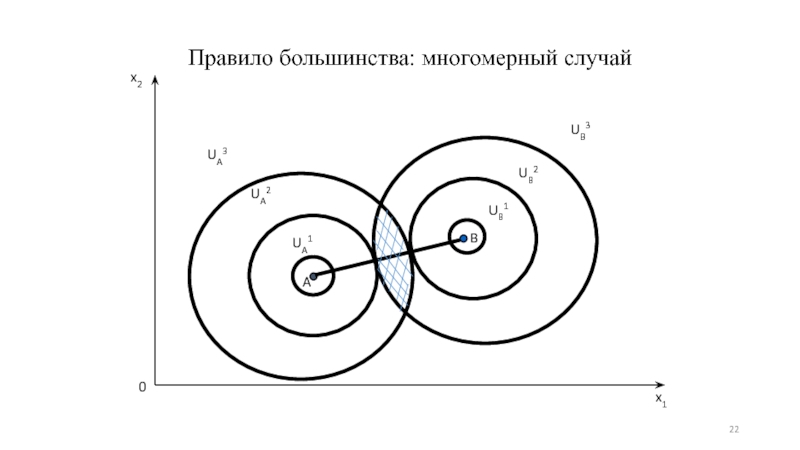
- 22. Правило большинства: многомерный случай 0
Слайд 2Правило единогласия
Правило единогласия – это правило голосования, согласно которому решение принимается
в том и только в том случае, если за него проголосуют все участвующие в голосовании.
Слайд 4Правило единогласия
Плюсы
Учитываются предпочтения всех членов общества
Ни одно из мнений не будет
проигнорировано
Парето-эффективно
Минусы
Временные издержки
Финансовые издержки
Издержки поиска компромисса
Вероятность несовпадения предпочтений – стремление скрывать предпочтения
Право вето у каждого голосующего
Парето-эффективно
Минусы
Временные издержки
Финансовые издержки
Издержки поиска компромисса
Вероятность несовпадения предпочтений – стремление скрывать предпочтения
Право вето у каждого голосующего
Слайд 5Референдумы в Швейцарии
Может ли возможность проводить в Швейцарии референдумы с небольшими
затратами и по широкому кругу вопросов помочь объяснить низкую активность швейцарских избирателей на выборах в парламент?
Слайд 6Правило большинства
Плюс использования правила большинства по сравнению с правилом единогласия –
снижение издержек.
Слайд 13Неравномерное распределение издержек и выгод при установке мусорных баков
При неравномерном распределении
выгод
Слайд 14Теорема Мэя
Функция группового принятия решений:
Где n – число индивидов в сообществе.
В
зависимости от предпочтительности для i-того члена сообщества одной из двух альтернатив x и y, Di принимает значения 1, 0 и -1 (при xPiy, xIiy и yPix, соответственно).
Слайд 16Теорема Мэя
Функция группового выбора есть правило простого большинства (и только оно),
если выполняются следующие четыре условия:
Достижимость результата: групповая функция решения принимает одно и только одно значение для каждой пары альтернатив.
Анонимность: изменение двух любых значений Di с -1 на 1 и с 1 на -1 оставляет сумму неизменной.
Достижимость результата: групповая функция решения принимает одно и только одно значение для каждой пары альтернатив.
Анонимность: изменение двух любых значений Di с -1 на 1 и с 1 на -1 оставляет сумму неизменной.
Слайд 17Теорема Мэя
Нейтральность: Если ранжирование сохраняется для любых двух пар альтернатив, то,
то таким же оно будет и при суммировании голосов/агрегировании предпочтений (если xRiy→zRiw для всех i, zRw).
Положительное реагирование/позитивный отклик: Если D=0, увеличение любого Di до 0 или 1 приводит к D>0.
Положительное реагирование/позитивный отклик: Если D=0, увеличение любого Di до 0 или 1 приводит к D>0.
Слайд 18Теорема Рэя – Тейлора
Если индивид, находясь в неведении относительно своего будущего
положения в обществе, принимает решение о выборе правила суммирования голосов, он выберет правило которое минимизирует вероятность поддержки им непринятого обществом варианта решения, максимизируя вероятность поддержки принятого решения. Таким правилом будет правило простого большинства.