СВЯЗИ.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виды связей. Методы их измерения презентация
Содержание
- 1. Виды связей. Методы их измерения
- 2. 1. ВИДЫ СВЯЗЕЙ. МЕТОДЫ ИХ ИЗМЕРЕНИЯ В
- 3. СВЯЗЬ МЕЖДУ ЯВЛЕНИЯМИ РАСКРЫВАЕТСЯ ЧЕРЕЗ СВЯЗЬ МЕЖДУ ПРИЗНАКАМИ
- 4. ВИДЫ СВЯЗЕЙ РАЗЛИЧАЮТ: 1. ФУНКЦИОНАЛЬНЫЕ ИЛИ ЖЕСТКО ДЕТЕРМИНИРОВАННЫЕ СВЯЗИ 2. СТОХАСТИЧЕСКИЕ ИЛИ СТАТИСТИЧЕСКИЕ СВЯЗИ
- 5. ФУНКЦИОНАЛЬНЫЕ СВЯЗИ ОСОБЕННОСТЬ ФУНКЦИОНАЛЬНЫХ СВЯЗЕЙ: определенному
- 6. ФУНКЦИОНАЛЬНЫЕ СВЯЗИ Функциональные связи характеризуются четким механизмом
- 7. СТОХАСТИЧЕСКИЕ СВЯЗИ При стохастических связях определенному значению
- 8. СТОХАСТИЧЕСКИЕ СВЯЗИ Например, при изучении урожайности зерновых,
- 9. Прямые и обратные связи По общему направлению
- 10. Связи бывают прямолинейные и криволинейные. Прямолинейные связи описываются уравнением прямой.
- 11. МЕТОДЫ ИЗУЧЕНИЯ СВЯЗЕЙ В статистике выделяют прямые
- 12. Косвенные методы Косвенные методы рассчитаны на статистические
- 13. 2. Аналитическая группировка. Показатели силы и тесноты
- 14. Метод параллельных рядов Суть его: приводятся 2
- 15. Пример для РФ за 2003 г.
- 16. С помощью метода параллельных рядов можно
- 17. Аналитическая группировка строится
- 18. Суть аналитической группировки Единицы совокупности объединяются в
- 19. ЭТАПЫ АНАЛИТИЧЕСКОЙ ГРУППИРОВКИ 1. данные группируются по
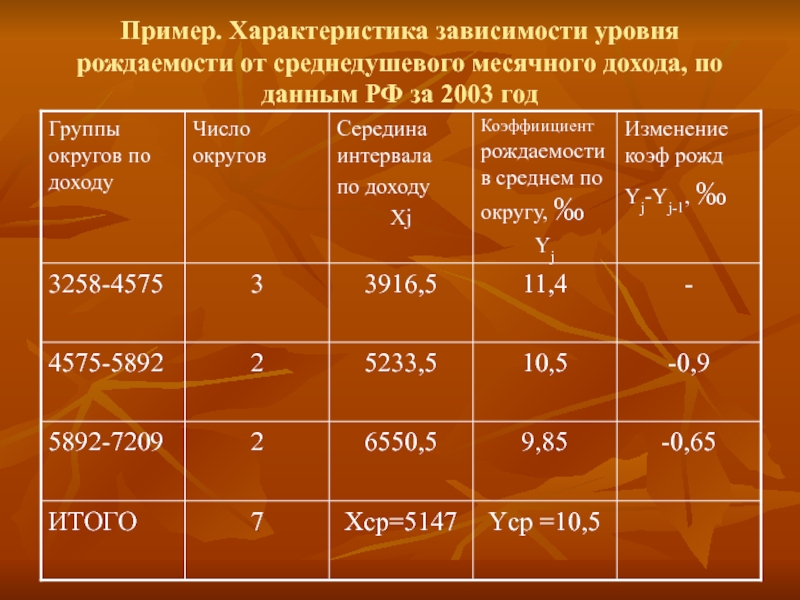
- 20. Пример. Характеристика зависимости уровня рождаемости от
- 21. Абсолютные показатели силы связи Группы округов по
- 22. Вывод о силе связи byx = -0,6
- 23. ПОКАЗАТЕЛИ ТЕСНОТЫ СВЯЗИ Поданным аналитической группировки можно
- 24. Шкала ЭКО Менее 0,1- связь практически отсутствует
- 25. Правило разложения дисперсии Э.К.О. основано на правиле
- 26. Расчет дисперсий Общая дисперсия σ2 =∑(Yi-Yср)2/n =
- 27. Э.к.о. и коэффициент детерминации ŋ2 =
Слайд 1ИЗУЧЕНИЕ СВЯЗЕЙ
ВИДЫ СВЯЗЕЙ. МЕТОДЫ ИХ ИЗМЕРЕНИЯ.
АНАЛИТИЧЕСКАЯ ГРУППИРОВКА. ПОКАЗАТЕЛИ СИЛЫ И ТЕСНОТЫ
Слайд 21. ВИДЫ СВЯЗЕЙ. МЕТОДЫ ИХ ИЗМЕРЕНИЯ
В процессе статистического изучения зависимостей выявляются
ПРИЧИННО-СЛЕДСТВЕННЫЕ отношения между явлениями.
При статистическом изучении зависимости не только выявляется НАЛИЧИЕ связи, но и определяется НАПРАВЛЕНИЕ связи, дается КОЛИЧЕСТВЕННАЯ ОЦЕНКА связи.
При статистическом изучении зависимости не только выявляется НАЛИЧИЕ связи, но и определяется НАПРАВЛЕНИЕ связи, дается КОЛИЧЕСТВЕННАЯ ОЦЕНКА связи.
Слайд 4ВИДЫ СВЯЗЕЙ
РАЗЛИЧАЮТ:
1. ФУНКЦИОНАЛЬНЫЕ ИЛИ ЖЕСТКО ДЕТЕРМИНИРОВАННЫЕ СВЯЗИ
2. СТОХАСТИЧЕСКИЕ ИЛИ СТАТИСТИЧЕСКИЕ СВЯЗИ
Слайд 5ФУНКЦИОНАЛЬНЫЕ СВЯЗИ
ОСОБЕННОСТЬ ФУНКЦИОНАЛЬНЫХ СВЯЗЕЙ:
определенному значению признака, который называется факторным, соответствует
строго определенное значение признака, называемого результативным (признаком-результатом).
Слайд 6ФУНКЦИОНАЛЬНЫЕ СВЯЗИ
Функциональные связи характеризуются четким механизмом взаимодействия признаков, который справедлив как
для отдельно взятой единицы совокупности, так и для всей совокупности в целом:
ПРИБЫЛЬ = РЕНТАБЕЛЬНОСТЬ ОК*СТОИМОСТЬ ОК
ВАЛОВОЙ СБОР = УРОЖАЙНОСТЬ*ПЛОЩАДЬ
ФОНД ЗАРАБОТНОЙ ПЛАТЫ=СР ЗАРПЛАТА 1 РАБОТНИКА*ЧИСЛЕННОСТЬ РАБОТНИКОВ
ПРИБЫЛЬ = РЕНТАБЕЛЬНОСТЬ ОК*СТОИМОСТЬ ОК
ВАЛОВОЙ СБОР = УРОЖАЙНОСТЬ*ПЛОЩАДЬ
ФОНД ЗАРАБОТНОЙ ПЛАТЫ=СР ЗАРПЛАТА 1 РАБОТНИКА*ЧИСЛЕННОСТЬ РАБОТНИКОВ
Слайд 7СТОХАСТИЧЕСКИЕ СВЯЗИ
При стохастических связях определенному значению признака-фактора могут соответствовать несколько значений
признака-результата.
Эти связи проявляются лишь в массе явлений, подчиняются только статистическим закономерностям, проявляются через случайное.
Механизм связи неизвестен.
Эти связи проявляются лишь в массе явлений, подчиняются только статистическим закономерностям, проявляются через случайное.
Механизм связи неизвестен.
Слайд 8СТОХАСТИЧЕСКИЕ СВЯЗИ
Например, при изучении урожайности зерновых, урожайность выступает как результативный признак.
В
качестве факторных могут выступать:
-качество почв, баллов
-количество внесенных удобрений, кг
- количество выпавших осадков, мм
- коэффициент готовности уборочной техники
- образование агронома, и т.д.
-качество почв, баллов
-количество внесенных удобрений, кг
- количество выпавших осадков, мм
- коэффициент готовности уборочной техники
- образование агронома, и т.д.
Слайд 9Прямые и обратные связи
По общему направлению выделяют прямые и обратные связи:
ПРЯМЫЕ
–когда факторный и результативный признаки меняются в одном направлении: объем продукции ↑, фондоотдача ↑; затраты на рекламу ↑, объем реализации ↑
ОБРАТНЫЕ – когда факторный и результативный признаки меняются в разных направлениях: объем продукции ↑, удельные постоянные издержки ↓
ОБРАТНЫЕ – когда факторный и результативный признаки меняются в разных направлениях: объем продукции ↑, удельные постоянные издержки ↓
Слайд 10
Связи бывают прямолинейные и криволинейные.
Прямолинейные связи описываются уравнением прямой.
Слайд 11МЕТОДЫ ИЗУЧЕНИЯ СВЯЗЕЙ
В статистике выделяют прямые и косвенные методы изучения связей.
ПРЯМЫЕ
методы применяются для жестко детерминированных связей. К ним относятся:
Метод средних величин;
Индексный метод;
Балансовый метод.
Метод средних величин;
Индексный метод;
Балансовый метод.
Слайд 12Косвенные методы
Косвенные методы рассчитаны на статистические виды связей.
К ним относятся:
Методы параллельных
рядов;
Аналитическая группировка;
Корреляционный и регрессионный анализ;
Дисперсионный анализ.
Аналитическая группировка;
Корреляционный и регрессионный анализ;
Дисперсионный анализ.
Слайд 132. Аналитическая группировка. Показатели силы и тесноты связи
Аналитическая группировка относится к
косвенным методам измерения статистических (стохастических) связей.
Построению аналитической группировки предшествует использование метода параллельных рядов.
Построению аналитической группировки предшествует использование метода параллельных рядов.
Слайд 14Метод параллельных рядов
Суть его: приводятся 2 ряда данных по двум признакам
(результат –коэффициент рождаемости; фактор –среднедушевой доход).
Данные ранжируются по признаку-фактору т.о., чтобы визуально оценить: как меняется признак-результат с изменением признака-фактора.
Данные ранжируются по признаку-фактору т.о., чтобы визуально оценить: как меняется признак-результат с изменением признака-фактора.
Слайд 16
С помощью метода параллельных рядов можно выявить наличие или отсутствие связи,
ее направление.
Однако, при большом объеме совокупности этот визуальный анализ становится трудновыполнимым,
и обращаются к самому простому способу обобщения: ГРУППИРОВКЕ.
Однако, при большом объеме совокупности этот визуальный анализ становится трудновыполнимым,
и обращаются к самому простому способу обобщения: ГРУППИРОВКЕ.
Слайд 17
Аналитическая группировка строится
По признаку-фактору = однофакторная
По признакам-факторам =
многофакторная
Слайд 18Суть аналитической группировки
Единицы совокупности объединяются в группы;
По каждой группе определяется среднее
значение результативного признака;
Сопоставляя изменения факторного признака с вариацией групповых средних по результативному признаку, можно сделать вывод о наличии или отсутствии связи.
В случае наличия связи, можно измерить ее силу и тесноту.
Сопоставляя изменения факторного признака с вариацией групповых средних по результативному признаку, можно сделать вывод о наличии или отсутствии связи.
В случае наличия связи, можно измерить ее силу и тесноту.
Слайд 19ЭТАПЫ АНАЛИТИЧЕСКОЙ ГРУППИРОВКИ
1. данные группируются по признаку-фактору, для каждой группы рассчитывается
среднее значение признака-результата.
2. На основе сопоставления изменений средних значений признака-результата по группам с изменением фактора делаются выводы о НАЛИЧИИ или ОТСУТСТВИИ связи между признаками.
3. чтобы эти изменения были сравнимыми, следует проводить группировку с равными интервалами, или, рассчитывать изменение результата на единицу изменения фактора.
2. На основе сопоставления изменений средних значений признака-результата по группам с изменением фактора делаются выводы о НАЛИЧИИ или ОТСУТСТВИИ связи между признаками.
3. чтобы эти изменения были сравнимыми, следует проводить группировку с равными интервалами, или, рассчитывать изменение результата на единицу изменения фактора.
Слайд 20 Пример. Характеристика зависимости уровня рождаемости от среднедушевого месячного дохода, по данным
РФ за 2003 год
Слайд 21Абсолютные показатели силы связи
Группы округов по доходу:
i=(xmax – xmin)/n = (7209-3258)/3=1317
руб.
Средний абсолютный показатель силы связи:
byx=(yn-y1)/(xn-x1)
9.85-11.4
byx= ------------ = -0,6 ‰
6.550-3.916
Средний абсолютный показатель силы связи:
byx=(yn-y1)/(xn-x1)
9.85-11.4
byx= ------------ = -0,6 ‰
6.550-3.916
Слайд 22Вывод о силе связи
byx = -0,6 ‰
Связь между явлениями обратная
При увеличении
среднедушевого дохода на 1 тыс рублей коэффициент рождаемости уменьшится в среднем на 0,6 промилле
Изменение среднедушевого дохода на 1 т.р. приводит к изменению коэффициента рождаемости на 0,6 ‰, в среднем, в обратном направлении
Изменение среднедушевого дохода на 1 т.р. приводит к изменению коэффициента рождаемости на 0,6 ‰, в среднем, в обратном направлении
Слайд 23ПОКАЗАТЕЛИ ТЕСНОТЫ СВЯЗИ
Поданным аналитической группировки можно измерить и тесноту связи между
признаками:
Она м.б. слабой, умеренной, заметной, тесной, очень тесной.
Это становится возможным при помощи показателя Эмпирическое Корреляционное Отношение (Э.К.О., обозначаемое греческой буквой «эта»- ŋ).
Она м.б. слабой, умеренной, заметной, тесной, очень тесной.
Это становится возможным при помощи показателя Эмпирическое Корреляционное Отношение (Э.К.О., обозначаемое греческой буквой «эта»- ŋ).
Слайд 24Шкала ЭКО
Менее 0,1- связь практически отсутствует
0,1-0,3 – слабая зависимость
0,3-0,5 – умеренная
связь
0,5-0,7 – значительная (заметная) связь
0,7-0,9 – высокая (тесная) связь
Более 0,9 –очень высокая (очень тесная) связь
0,5-0,7 – значительная (заметная) связь
0,7-0,9 – высокая (тесная) связь
Более 0,9 –очень высокая (очень тесная) связь
Слайд 25Правило разложения дисперсии
Э.К.О. основано на правиле разложения дисперсии:
Общая дисперсия = межгрупповая
(факторная) + внутригрупповая (остаточная).
σ2 = δ2 + s2
Смысл этого разложения: дисперсия (вариация) изучаемого признака σ2 обусловлена изменением (вариацией) учтенного фактора (факторов) δ2 и изменением неучтенных в модели факторов s2.
σ2 = δ2 + s2
Смысл этого разложения: дисперсия (вариация) изучаемого признака σ2 обусловлена изменением (вариацией) учтенного фактора (факторов) δ2 и изменением неучтенных в модели факторов s2.
Слайд 26Расчет дисперсий
Общая дисперсия
σ2 =∑(Yi-Yср)2/n = (Y2)ср –(Yср)2
σ2 = 1.20
Факторная дисперсия –
дисперсия признака-результата, объясненная учтенным признаком-фактором
δ2 =∑(Yj-Yср)2 nj/∑nj = 0.468
δ2 =∑(Yj-Yср)2 nj/∑nj = 0.468
Слайд 27Э.к.о. и коэффициент детерминации
ŋ2 = δ2 / σ2 –коэффициент детерминации, показывает
долю (%) общей дисперсии, объясненной колеблемостью факторного признака
ŋ2 = 0,468/1,2=0,39 или 39% -
Т.о., 39% вариации рождаемости в изучаемых округах обусловлено вариацией уровня дохода, остальные 61% вариации результативного признака обусловлены действием прочих, кроме Х, неучтенных факторов.
ŋ = √ (δ2 / σ2) = √0,39 =0,62 –между X и Y наблюдается значительная (заметная) связь
ŋ2 = 0,468/1,2=0,39 или 39% -
Т.о., 39% вариации рождаемости в изучаемых округах обусловлено вариацией уровня дохода, остальные 61% вариации результативного признака обусловлены действием прочих, кроме Х, неучтенных факторов.
ŋ = √ (δ2 / σ2) = √0,39 =0,62 –между X и Y наблюдается значительная (заметная) связь