Д.с.н, к.ф.-м.н. Шведовский В.А.
НИЛ «Математическое моделирование и информатика социальных процессов
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
методике построения социальных прогнозов на топологических цепях Маркова, основе обобщения модели К.Левина. (Лекция 6) презентация
Содержание
- 1. методике построения социальных прогнозов на топологических цепях Маркова, основе обобщения модели К.Левина. (Лекция 6)
- 2. Левин (Lewin) Курт
- 3. Первый шаг построения жизненного пространства личности по
- 4. Второй шаг построения жизненного пространства личности по
- 5. Модель К.Левина жизненного пространства личности (ЖПЛ) L
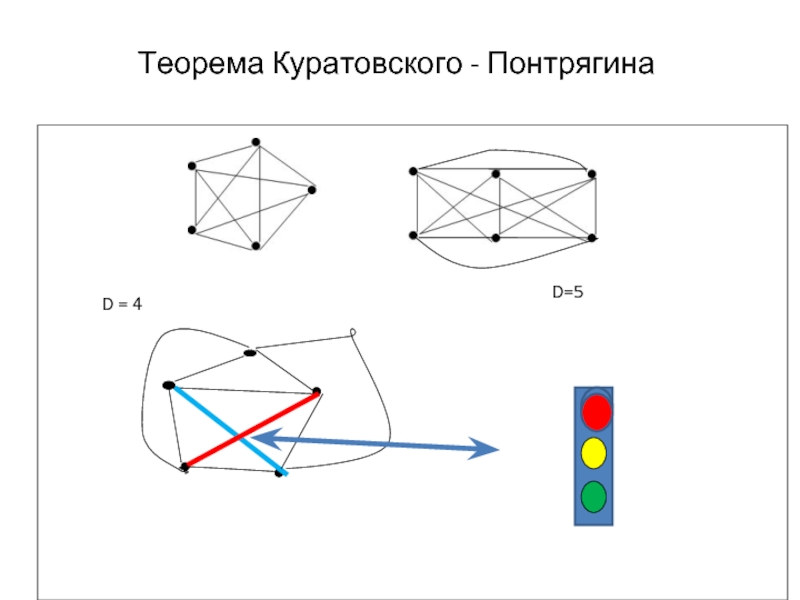
- 6. Теорема Куратовского - Понтрягина
- 7. Основные идеи выстраиваемой методологии 1) Вероятностное поведение
- 8. n Классификаторы
- 9. Классификатор Зворыкина А.А.
- 10. Шкалы для представления идеала (студенты – заочники
- 11. Шкалы семантического дифференциала и актуальность многомерного куба
- 12. Минимальная сеть - граф 4-х куба для
- 13. Построение многомерной сети Отобразим связи между
- 14. Сферическая поверхность - род «γ=0» и граф
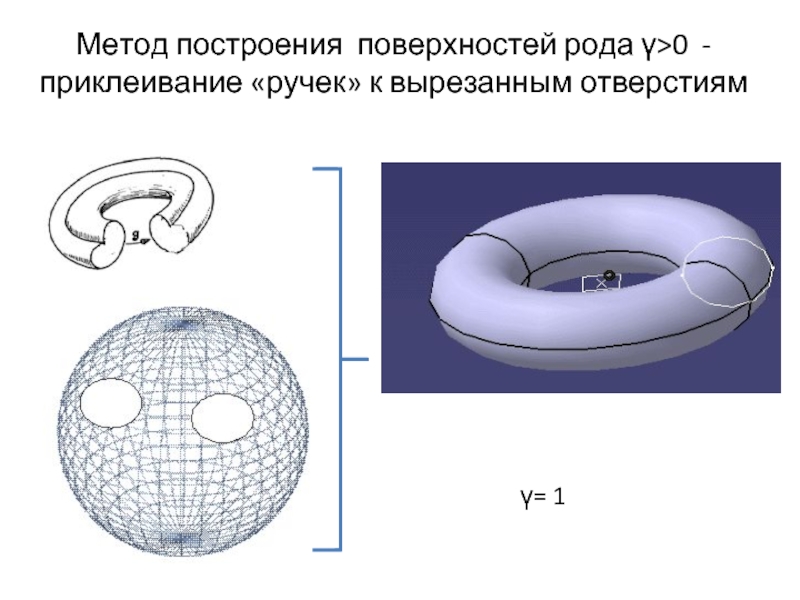
- 15. Метод построения поверхностей рода γ>0 - приклеивание «ручек» к вырезанным отверстиям γ= 1
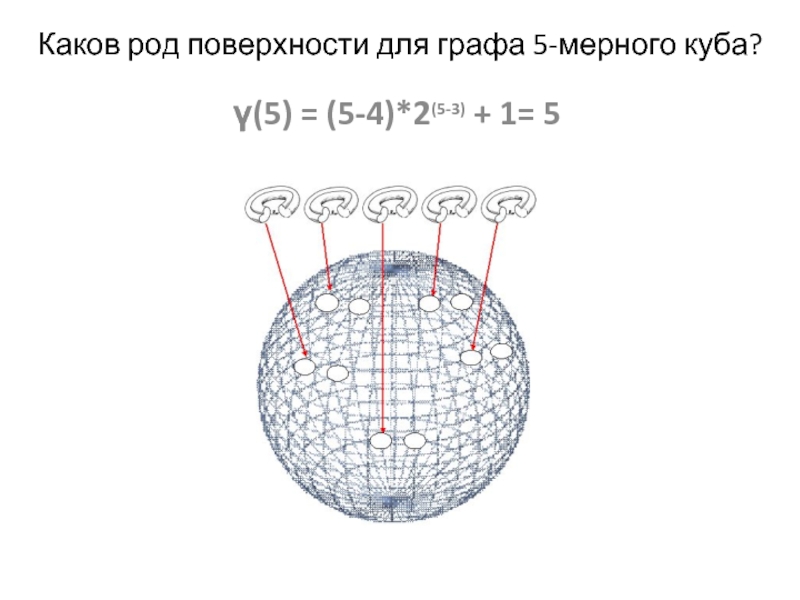
- 16. Каков род поверхности для графа 5-мерного куба? γ(5) = (5-4)*2(5-3) + 1= 5
- 17. Вид минимальной «безсветофорной» сети для пространства личности
- 18. Оценки min числа неустранимых рёберных пересечений для
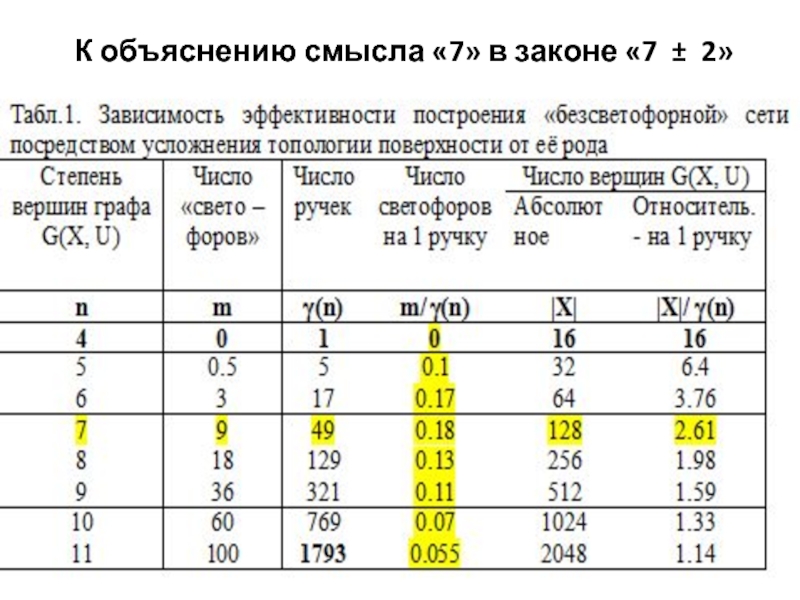
- 19. К объяснению смысла «7» в законе «7 ± 2»
- 20. Годологический проект К. Левина (3, 4, 5,
- 21. Связь с гауссовой кривизной характеристика Эйлера-Пуанкаре связана
- 22. ∫Кds -интеграл по поверхности сопряжения ручки со
- 23. Без симметрии n – n(n-1) + F
- 24. Характеристика Эйлера-Пуанкаре χ графа многомерной сети
- 25. Теорема о мере максимальной энтропии для ТМЦ
- 26. Марковские процессы A1(s), A2(s),…, Ak(s) –
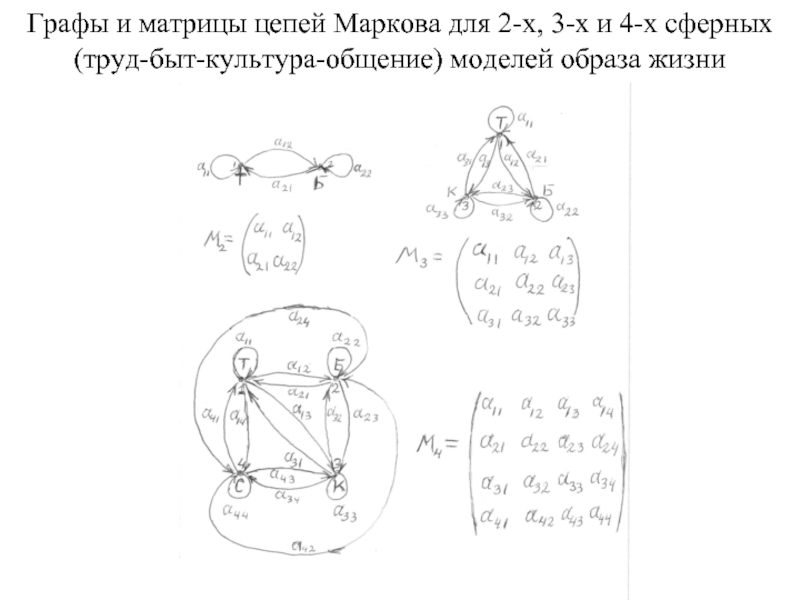
- 27. Графы и матрицы цепей Маркова для 2-х,
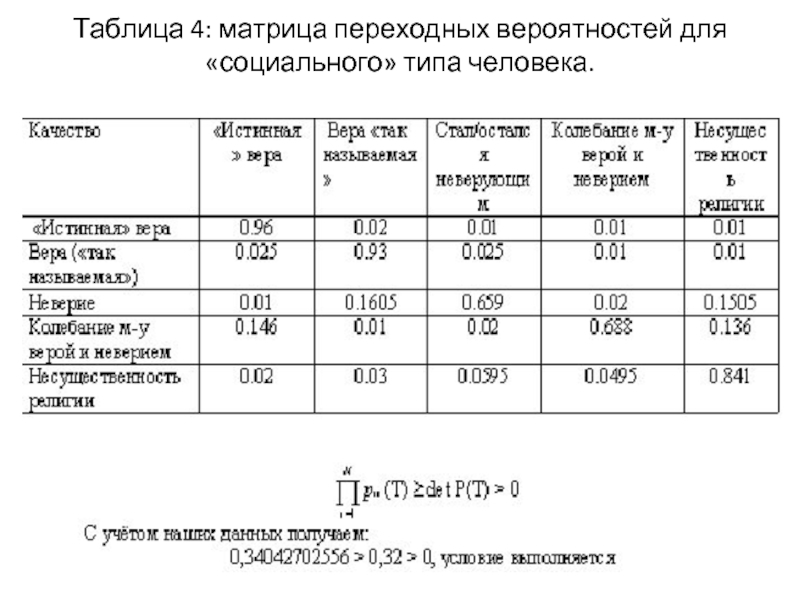
- 28. Таблица 4: матрица переходных вероятностей для «социального» типа человека.
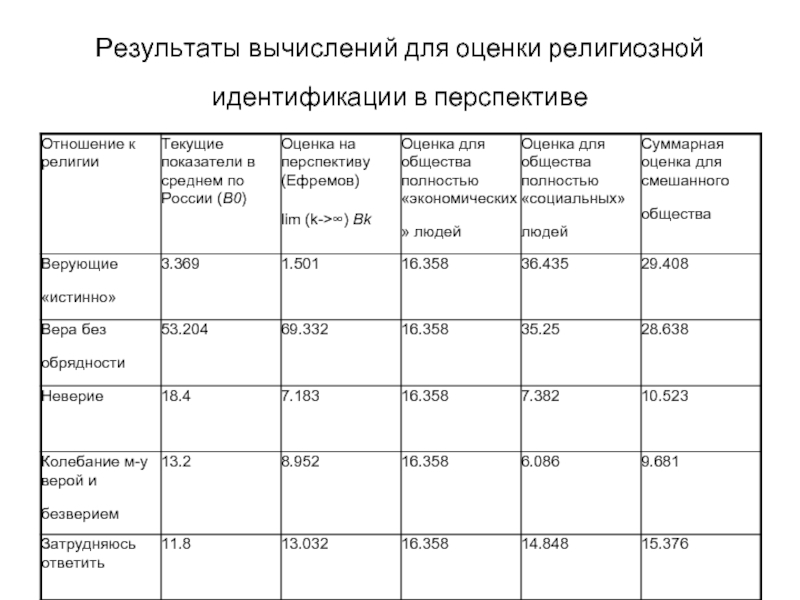
- 29. Результаты вычислений для оценки религиозной идентификации в перспективе
Слайд 1Лекция 6: К методике построения социальных прогнозов на топологических цепях Маркова
Слайд 2Левин (Lewin) Курт
(09.09.1890, Познань - 12.02.1947, Ньютон, США) - немецкий и
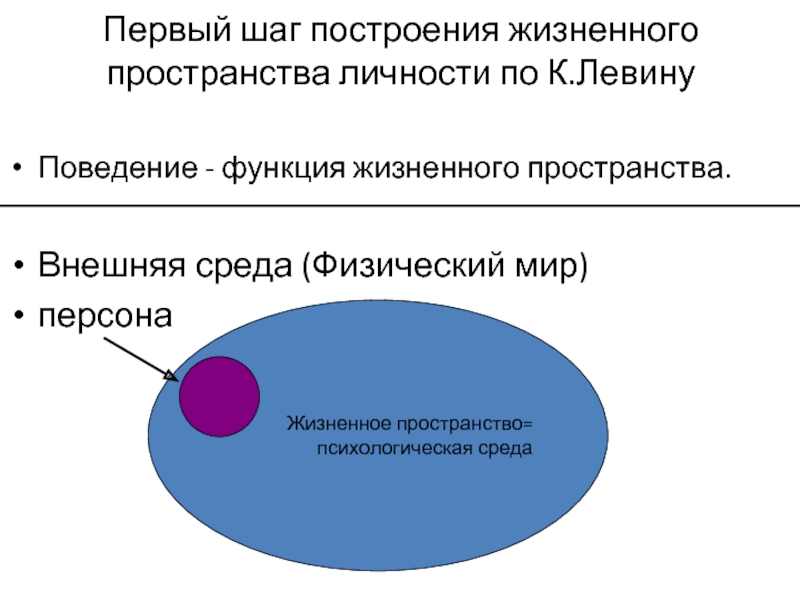
Слайд 3Первый шаг построения жизненного пространства личности по К.Левину
Поведение - функция жизненного
Внешняя среда (Физический мир)
персона
Жизненное пространство=
психологическая среда
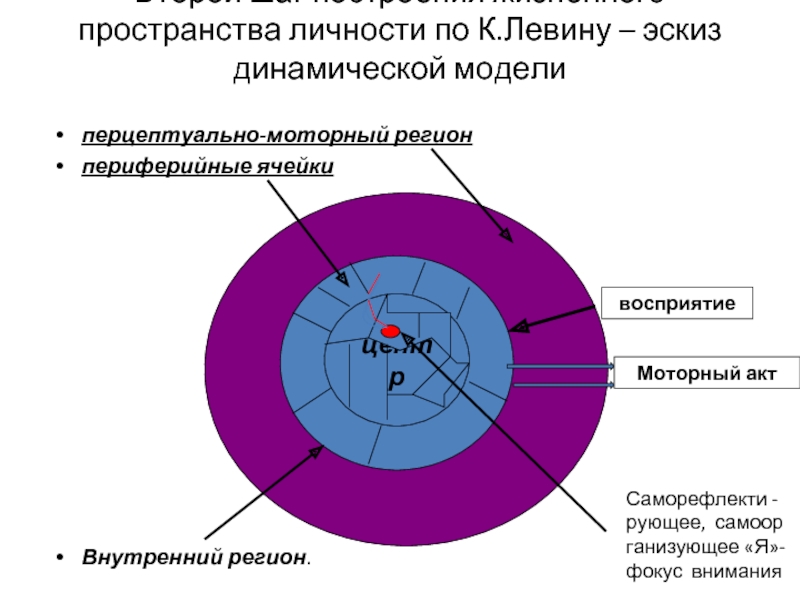
Слайд 4Второй шаг построения жизненного пространства личности по К.Левину – эскиз динамической
перцептуально-моторный регион
периферийные ячейки
Внутренний регион.
центр
восприятие
Моторный акт
Саморефлекти - рующее, самоор ганизующее «Я»-фокус внимания
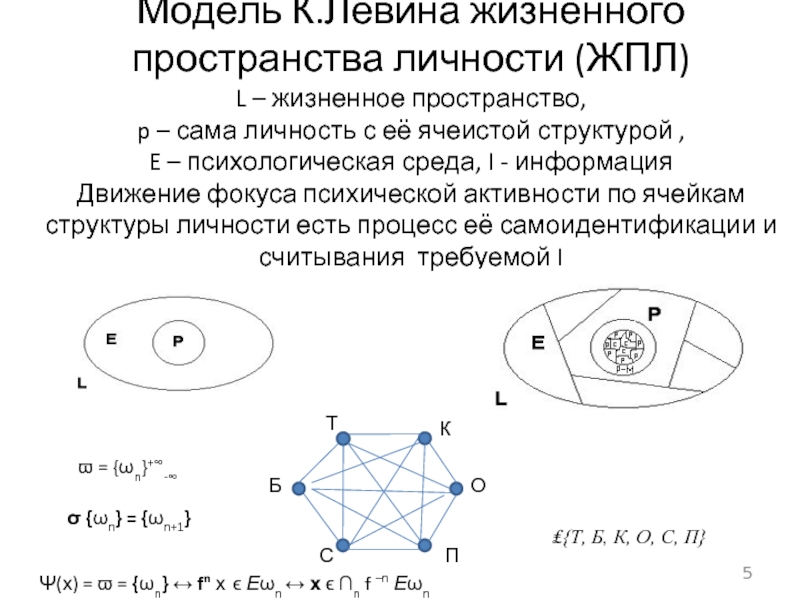
Слайд 5Модель К.Левина жизненного пространства личности (ЖПЛ) L – жизненное пространство, p –
Т
Б
К
О
С
П
σ {ωn} = {ωn+1}
ϖ = {ωn}+∞-∞
Ψ(х) = ϖ = {ωn} ↔ fn х ϵ Еωn ↔ х ϵ ∩n f –n Еωn
₤{Т, Б, К, О, С, П}
Слайд 7Основные идеи выстраиваемой методологии
1) Вероятностное поведение личности определяется её установками
2) Установки
3) Прогноз для группы = прогнозу для её типичной личности
4) Траектории личности в жизни = траекториям в её ЖПЛ
5) Нет необходимости выписывать уравнения этих траекторий
6) Достаточно знания орграфа связей между 6 сферами образа жизни
7) Полный 6-орграф организует трафики без пересечений на 2- мерной компактной, ориентированной поверхности рода р ≥ 2, т.е. с К < 0
8) Эта координатная составляющая фазового пространства д.с. – см. 5) порождает гиперболическую динамическую систему – г.д.с.
9) Особенности г.д.с., а т.е. и гомоклинические и гетероклинические траектории изоморфно изучаемы на траекториях бильярдов, и они отождествляются с вершинами орграфа, что порождает ТМЦ
Слайд 8 n
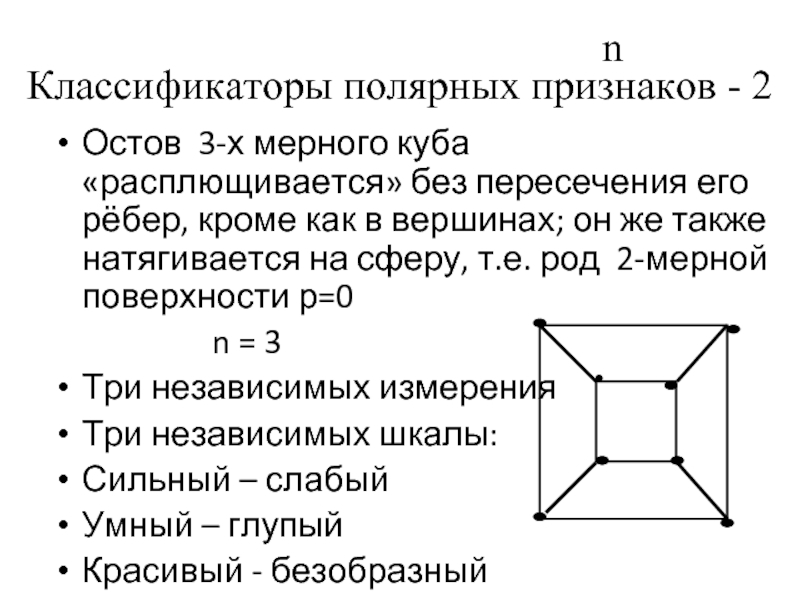
Классификаторы полярных признаков - 2
Остов 3-х
n = 3
Три независимых измерения
Три независимых шкалы:
Сильный – слабый
Умный – глупый
Красивый - безобразный
Слайд 9Классификатор Зворыкина А.А.
2 4
лз
Личность преступника
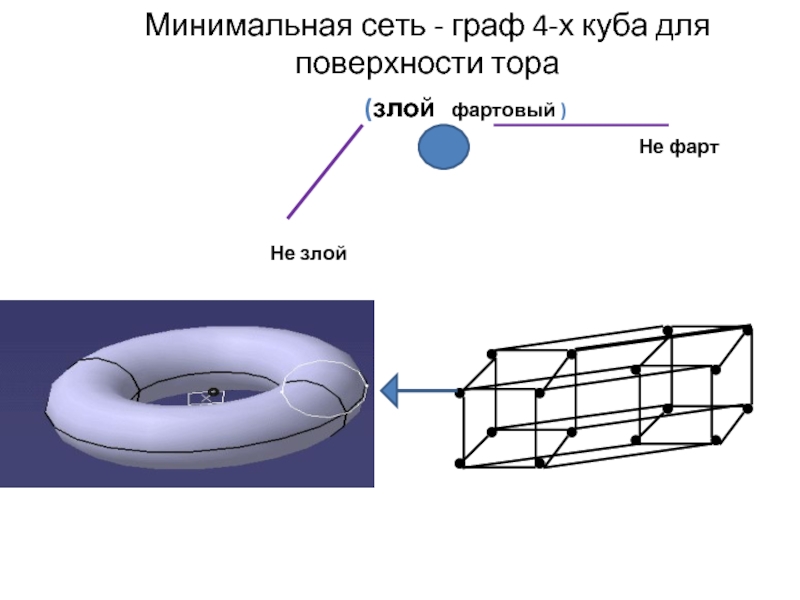
Злой – не злой; фартовый – не фартовый
Слайд 10Шкалы для представления идеала (студенты – заочники (27-30 лет) – вуз
Л.К. М.Х.
1: душевный - черствый 1: добрый - злой
2: аккуратный - неряшливый 2: умный - глупый
3: волевой - безвольный 3: простодушный - хитрый
4: трудолюбивый - ленивый 4: красивый - страшный
5: нервный - спокойный 5: мягкий - жесткий
И.Д. И.К.
1:самостоятельный - зависимый 1: умный - глупый
2:храбрый - робкий 2:смелый - трусливый
3:доверчивый - подозрительный 3:общительный - замкнутый
4:безмятежный - тревожный 4:внимательный - рассеянный
5:интеллектуальный – туповатый 5: активный - пассивный
В.У. Т.З.
1: добрый - злой 1: трудолюбивый - ленивый
2: умный - глупый 2: спокойный - «шебутной»
3: быстрый - медлительный 3: собранный - разгильдяй
4: красивый - «страшный» 4: удачливый - невезучий
5:молчаливый - разговорчивый 5: сообразительный – тугодум
2 5
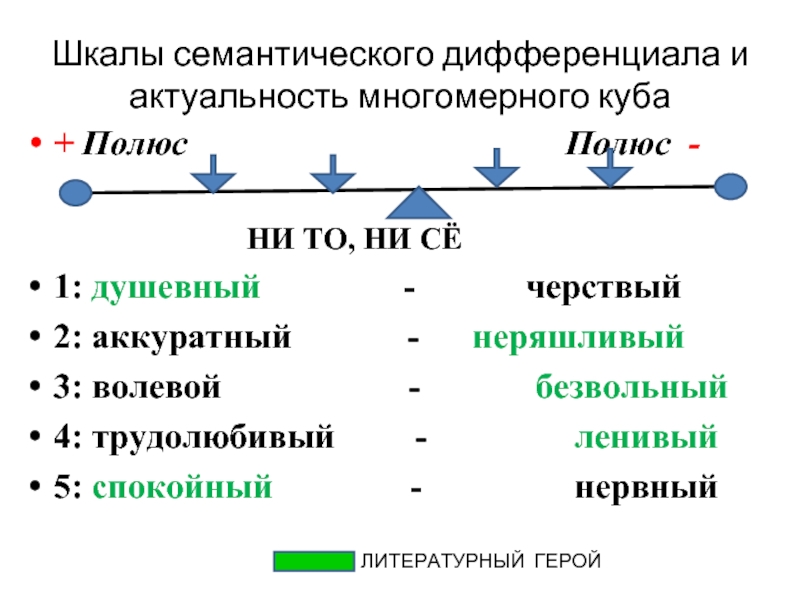
Слайд 11Шкалы семантического дифференциала и актуальность многомерного куба
+ Полюс
НИ ТО, НИ СЁ
1: душевный - черствый
2: аккуратный - неряшливый
3: волевой - безвольный
4: трудолюбивый - ленивый
5: спокойный - нервный
ЛИТЕРАТУРНЫЙ ГЕРОЙ
+
Слайд 13Построение многомерной сети
Отобразим связи между регионами ЖПЛ, образующими компактную целостность,
γ(n) = (n-4)*2(n-3) + 1
Байнеке Л.В., Харари Ф. (1974)
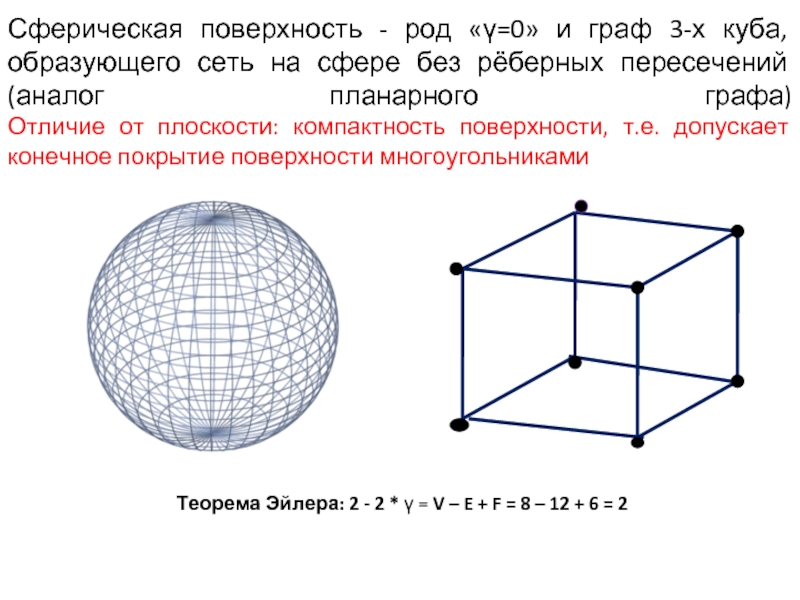
Слайд 14Сферическая поверхность - род «γ=0» и граф 3-х куба, образующего сеть
Теорема Эйлера: 2 - 2 * γ = V – E + F = 8 – 12 + 6 = 2
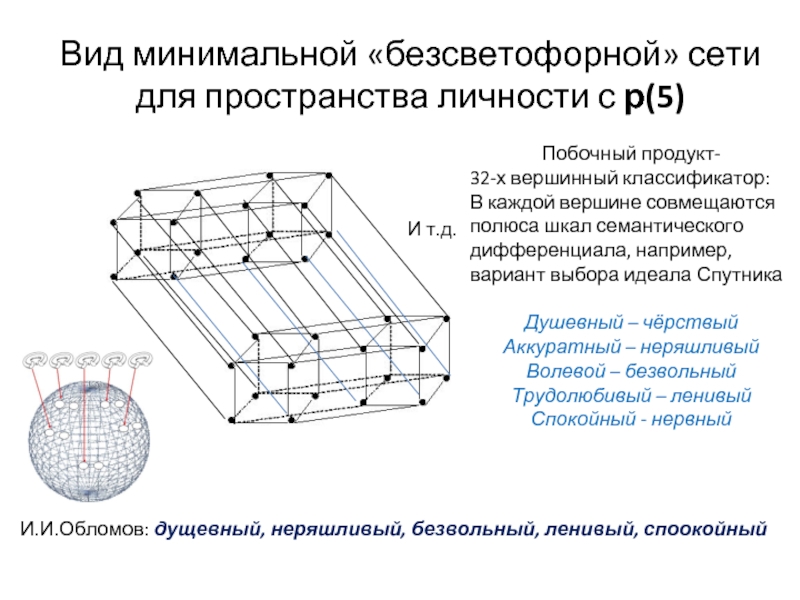
Слайд 17Вид минимальной «безсветофорной» сети для пространства личности с р(5)
И т.д.
Побочный
32-х вершинный классификатор:
В каждой вершине совмещаются
полюса шкал семантического
дифференциала, например,
вариант выбора идеала Спутника
Душевный – чёрствый
Аккуратный – неряшливый
Волевой – безвольный
Трудолюбивый – ленивый
Спокойный - нервный
И.И.Обломов: дущевный, неряшливый, безвольный, ленивый, споокойный
Слайд 18 Оценки min числа неустранимых рёберных пересечений для обыкновенных графов, расположенных на
это наименьшее число, согласно Т.Саати (1964), не превосходит
1/64 * n* (n-2)2 * (n-4) - при n чётном
и не превосходит
1/64 * (n-1)2 * (n-3)2 - при n нечётном
Слайд 20Годологический проект К. Левина
(3, 4, 5, 6 и 7 шаги)
Недостаточность топологического
Оснащение топологии пространства личности векторами, которые связаны с понятиями валентности регионов пространства и силой, вводит в него динамику.
Слайд 21Связь с гауссовой кривизной
характеристика Эйлера-Пуанкаре связана со средним по поверхности от
∫КdS = 2π χ
Слайд 22∫Кds -интеграл по поверхности сопряжения ручки со сферой
∫К- ds =
Проблема
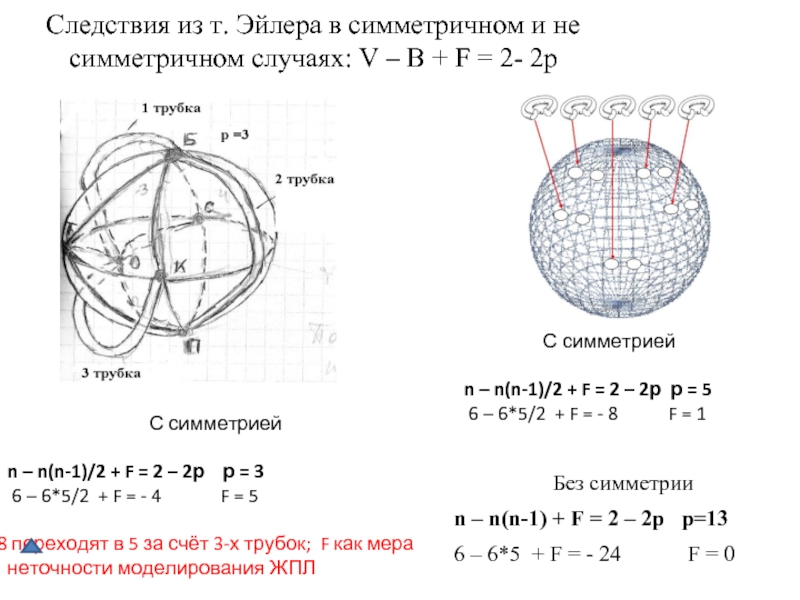
Слайд 23Без симметрии
n – n(n-1) + F = 2 – 2р
6 – 6*5 + F = - 24 F = 0
Следствия из т. Эйлера в симметричном и не симметричном случаях: V – B + F = 2- 2p
С симметрией
n – n(n-1)/2 + F = 2 – 2р р = 5
6 – 6*5/2 + F = - 8 F = 1
С симметрией
n – n(n-1)/2 + F = 2 – 2р р = 3
6 – 6*5/2 + F = - 4 F = 5
переходят в 5 за счёт 3-х трубок; F как мера неточности моделирования ЖПЛ
Слайд 24Характеристика Эйлера-Пуанкаре χ графа
многомерной сети на поверхности рода р
Эта характеристика
χ = 2 – 2р = 2 – (n-4)*2(n-2) – 2 = (4-n)*2(n-2)
Слайд 25Теорема о мере максимальной энтропии для ТМЦ
Пусть ТМЦ (ΣА) неразложима. Тогда
h μ0 (σ) = h(σІΣА) = logλ(A).
Эта мера совпадает с распределением вероятностей, отвечающим стационарной цепи Маркова с вероятнос - тями перехода
pij = aij zj / λ(A)*zi ,
где λ(A) – максимальное положительное собственное число матрицы А, а Z = {zi} - соответствующий собствен
ный вектор.
Слайд 26Марковские процессы
A1(s), A2(s),…, Ak(s) – несовместимые события, s- номер испытания
P (Ai(s+1)) зависит только от Aj(s)
Вектор начального состояния B0
Матрица переходных вероятностей Pij
Вероятность перехода из состояния i в состоянии j за t тактов времени
pij(t) = piq(t-1) ⋅ pqj
Матрицы переходных вероятностей для каждого случая
Вектор начального распределения – 2005 г.
Вектор стационарного распределения