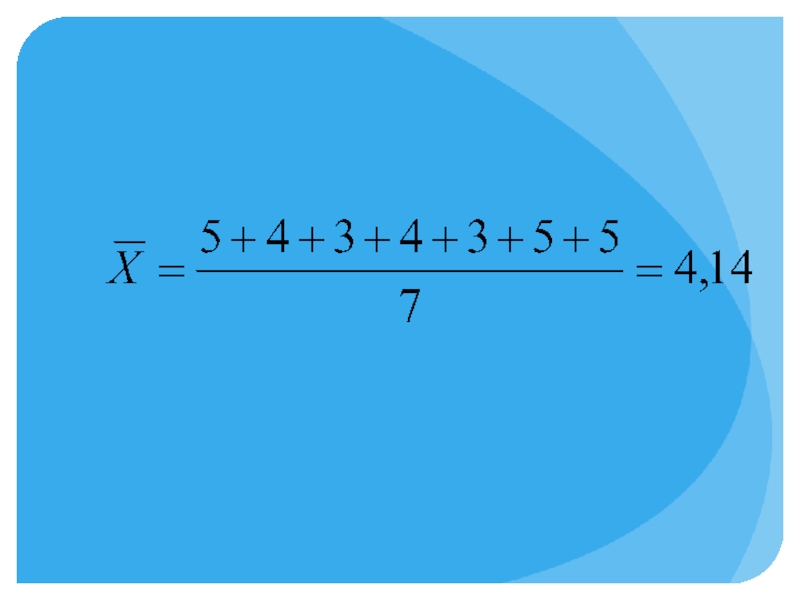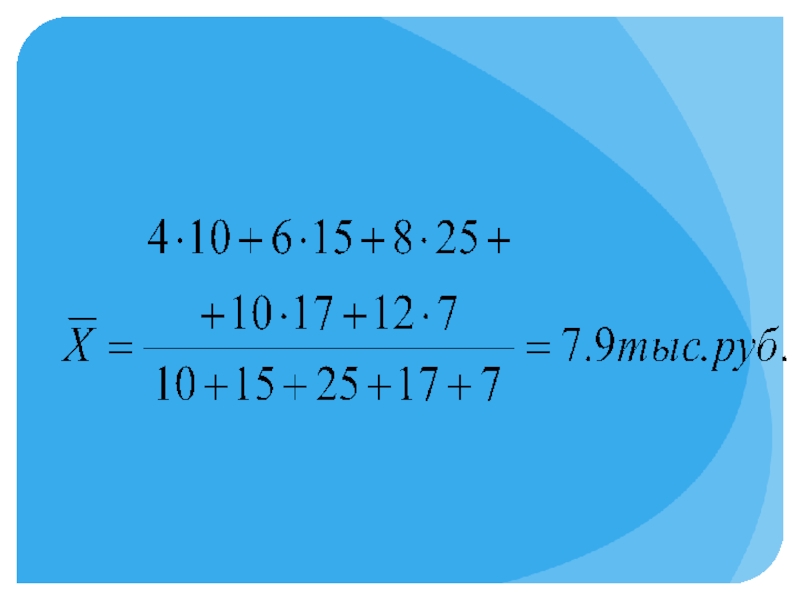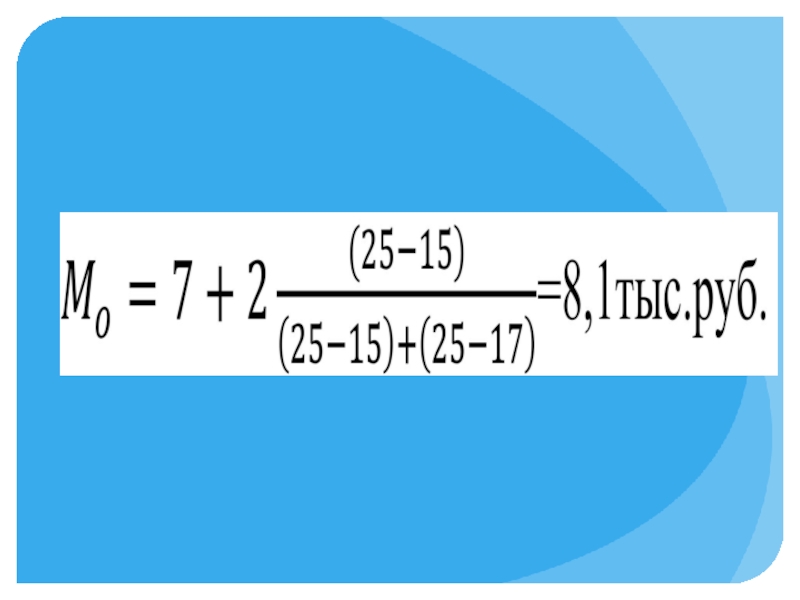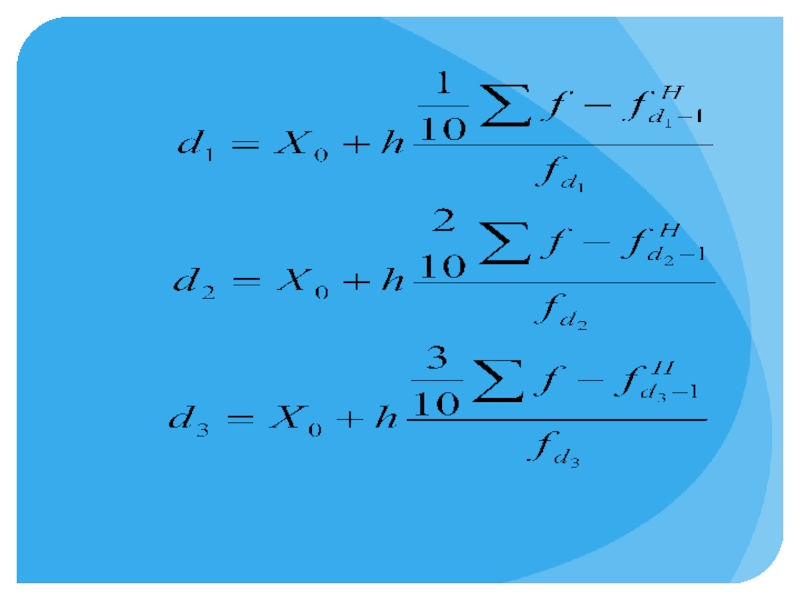- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Средние статистические показатели презентация
Содержание
- 1. Средние статистические показатели
- 2. Статистический показатель - это объективная, обобщающая
- 3. Статистические показатели по форме выражения: Абсолютные Относительные Средние
- 4. Средним показателем называется величина, которая выражает типичные
- 5. Виды средних показателей: Средняя арифметическая Средняя гармоническая Средняя хронологическая Средняя геометрическая Средняя квадратическая (степенная средняя)
- 6. Исходное соотношение средней (ИСС)
- 7. Средняя арифметическая простая взвешенная
- 8. Средняя Арифметическая простая
- 9. Иванов 5 Смирнов 4 Сотникова 3 Петров 4 Рыбаков 3 Курочкин 5
- 12. Средняя арифметическая взвешенная
- 13. По данным о заработной плате рабочих промышленного предприятия рассчитайте среднюю заработную плату:
- 16. Средняя гармоническая: простая взвешенная
- 17. Средняя гармоническая простая:
- 18. Например: В отделе заказов торговой фирмы занято
- 19. Решение:
- 21. Средняя гармоническая взвешенная: Где wi=xifi
- 22. Имеются следующие данные об урожайности зерновых культур
- 25. Средняя квадратическая (степенная средняя) или
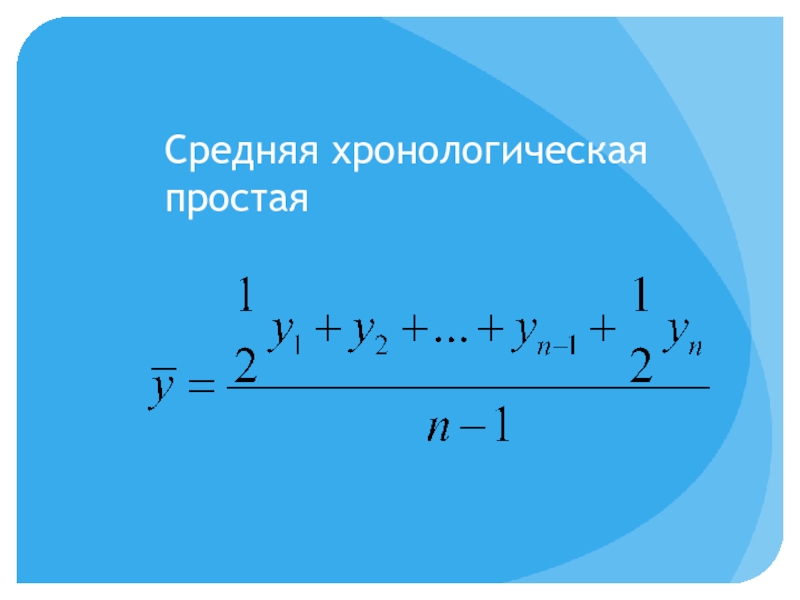
- 26. Средняя хронологическая Простая взвешенная
- 27. Средняя хронологическая простая
- 28. Средняя хронологическая взвешенная
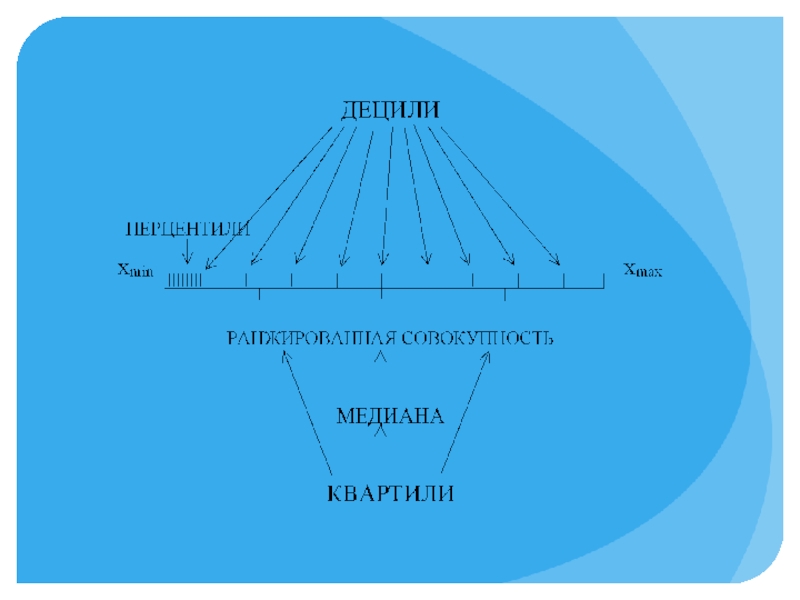
- 29. Структурные средние Мода Медиана Квартили Децили перцили
- 30. Мода – это значение признака, которое наиболее часто встречается в совокупности
- 31. 1. Если исходные данные не сгруппированы, то
- 32. Например: Результаты сдачи экзамена по статистики одной из студенческих групп: 5,2,4,2,3,2,2,2 Мо=2
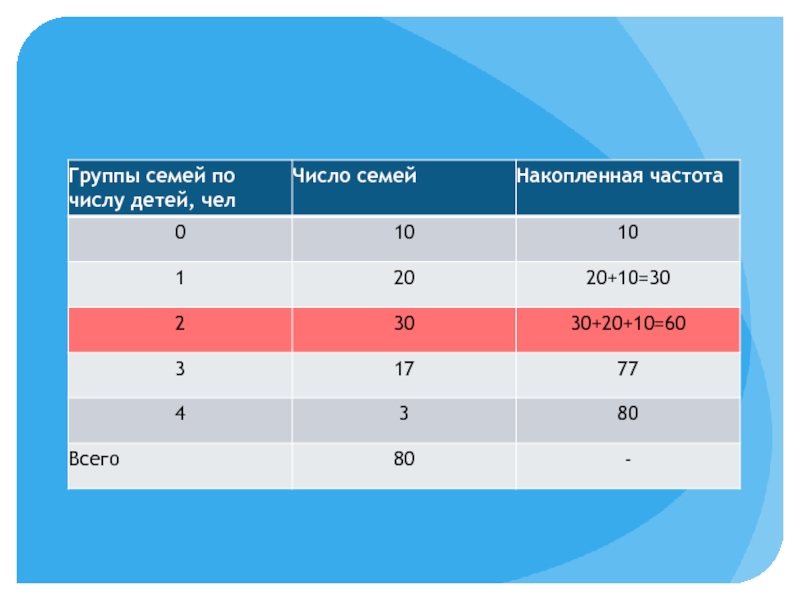
- 33. 2. Если исходные данные представлены в виде
- 35. Если исходные данные представлены в виде интервального вариационного ряда распределения Мода
- 38. Медиана – это значение признака, которое стоит в середине упорядоченной совокупности
- 39. Если исходные данные не сгруппированы и представлены
- 40. Например: Результаты сдачи экзамена по статистики одной
- 41. Например: Результаты сдачи экзамена по статистики одной
- 42. 2. Если исходные данные представлены в виде
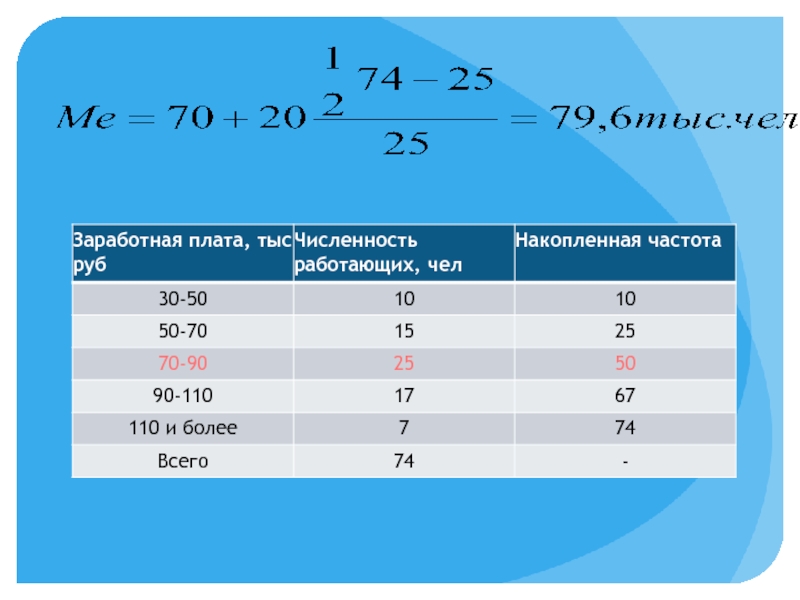
- 44. 3. Если исходные данные представлены в виде интервального вариационного ряда распределения
- 48. Квартили – это значение признака, которое делят совокупность на четыре равные части
- 49. Если исходные данные не сгруппированы и представлены
- 50. 2. Если исходные данные представлены в виде
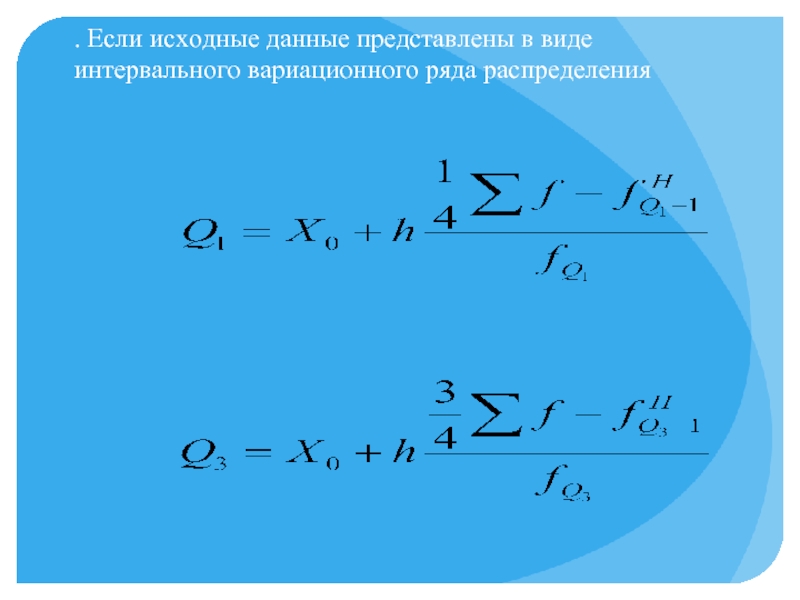
- 51. . Если исходные данные представлены в виде интервального вариационного ряда распределения
- 52. Децили – это значение признака, которое делят совокупность на десять равных частей
Слайд 2Статистический показатель -
это объективная, обобщающая количественная характеристика явления или процесса
в его качественном определении, т.е. с социально-экономическим содержанием, в конкретных условиях места и времени.
Слайд 4Средним показателем
называется величина, которая выражает типичные черты и дает обобщающую количественную
характеристику социально-экономического явления по одному варьирующему признаку
Слайд 5Виды средних показателей:
Средняя арифметическая
Средняя гармоническая
Средняя хронологическая
Средняя геометрическая
Средняя квадратическая (степенная средняя)
Слайд 9
Иванов 5
Смирнов 4
Сотникова 3
Петров 4
Рыбаков 3
Курочкин 5
Селезнев 5
По результатам сдачи экзаменов по Теории статистики рассчитайте средний балл:
Слайд 13По данным о заработной плате рабочих промышленного предприятия рассчитайте среднюю заработную
плату:
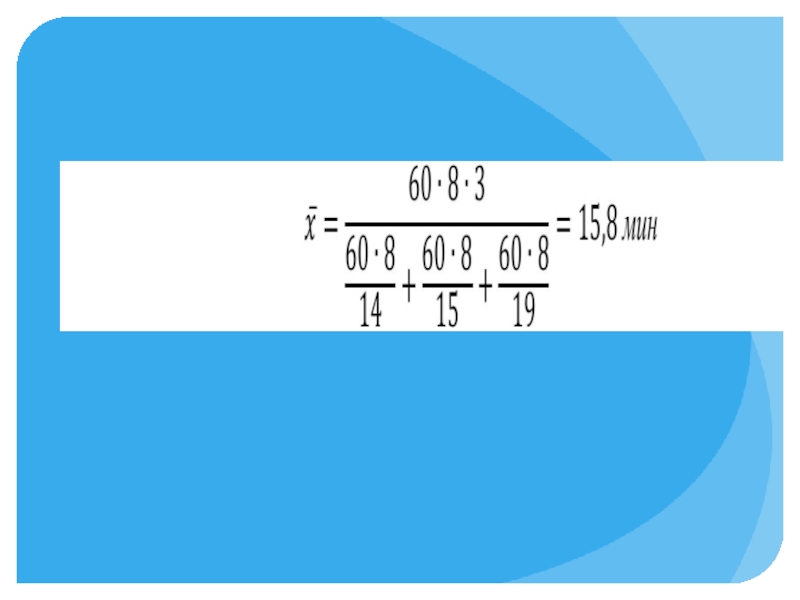
Слайд 18Например:
В отделе заказов торговой фирмы занято трое работников, имеющих 8-часовой рабочий
день. Первый работник на оформление одного заказа в среднем затрачивает 14 мин., второй - 15 мин., третий - 19 мин. Определите средние затраты времени на 1 заказ в целом по отделу.
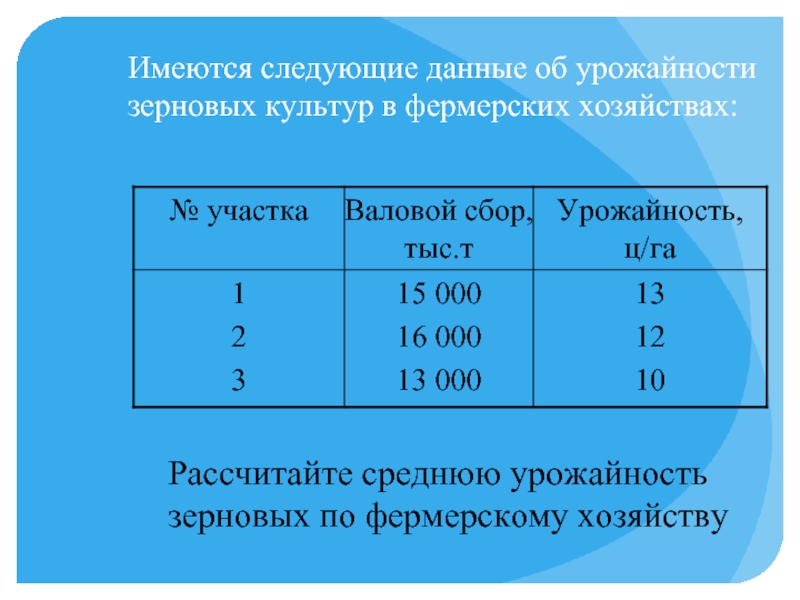
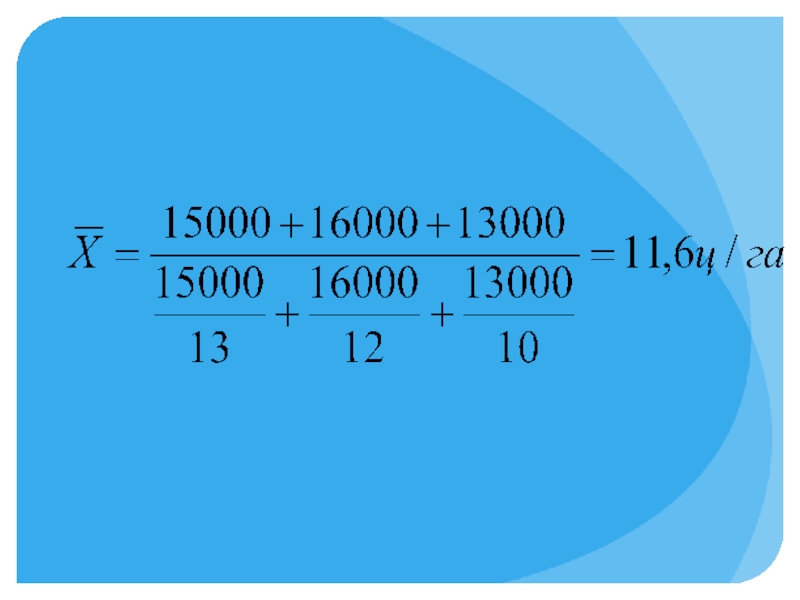
Слайд 22Имеются следующие данные об урожайности зерновых культур в фермерских хозяйствах:
Рассчитайте среднюю
урожайность
зерновых по фермерскому хозяйству
зерновых по фермерскому хозяйству
Слайд 311. Если исходные данные не сгруппированы, то модальным будет называться значение
признака, наиболее часто встречающееся в совокупности
Слайд 32Например:
Результаты сдачи экзамена по статистики одной из студенческих групп:
5,2,4,2,3,2,2,2
Мо=2
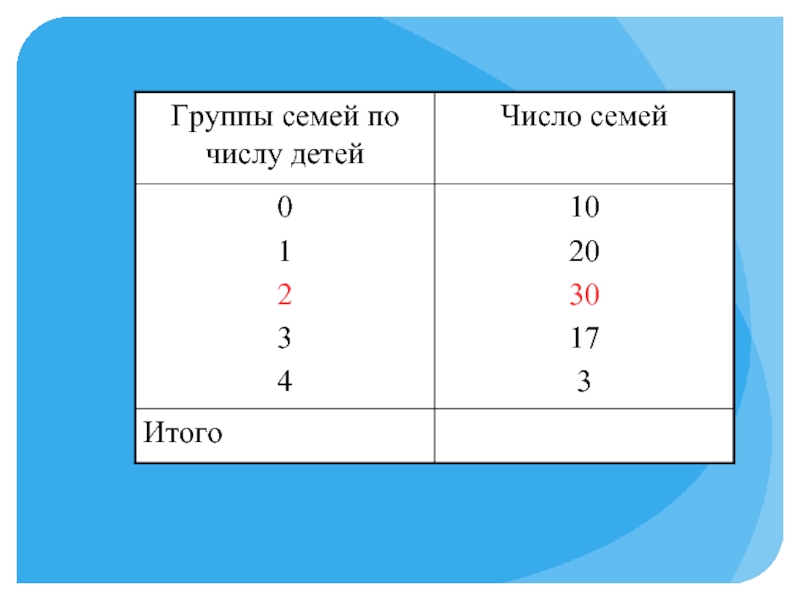
Слайд 332. Если исходные данные представлены в виде дискретного вариационного ряда распределения,
то модальным будет называться значение признака с максимальной частотой.
Слайд 39Если исходные данные не сгруппированы и представлены в виде числовой последовательности,
то:
- Если нечетное количество единиц совокупности, то медианой будет называться значение стоящее в середине упорядоченной совокупности
- Если четное количество единиц совокупности, то медиана определяется как среднее значение из двух в середине стоящих значений упорядоченной совокупности
- Если нечетное количество единиц совокупности, то медианой будет называться значение стоящее в середине упорядоченной совокупности
- Если четное количество единиц совокупности, то медиана определяется как среднее значение из двух в середине стоящих значений упорядоченной совокупности
Слайд 40Например:
Результаты сдачи экзамена по статистики одной из студенческих групп:
5,2,4,2,3,2,2,2,5
Необходимо упорядочить
совокупность
2 2 2 2 2 3 4 5 5
Ме=2
2 2 2 2 2 3 4 5 5
Ме=2
Слайд 41Например:
Результаты сдачи экзамена по статистики одной из студенческих групп:
5,2,4,2,3,2,2,2,5,5
Необходимо упорядочить
совокупность
2 2 2 2 2 3 4 5 5 5
Ме=2,5
2 2 2 2 2 3 4 5 5 5
Ме=2,5
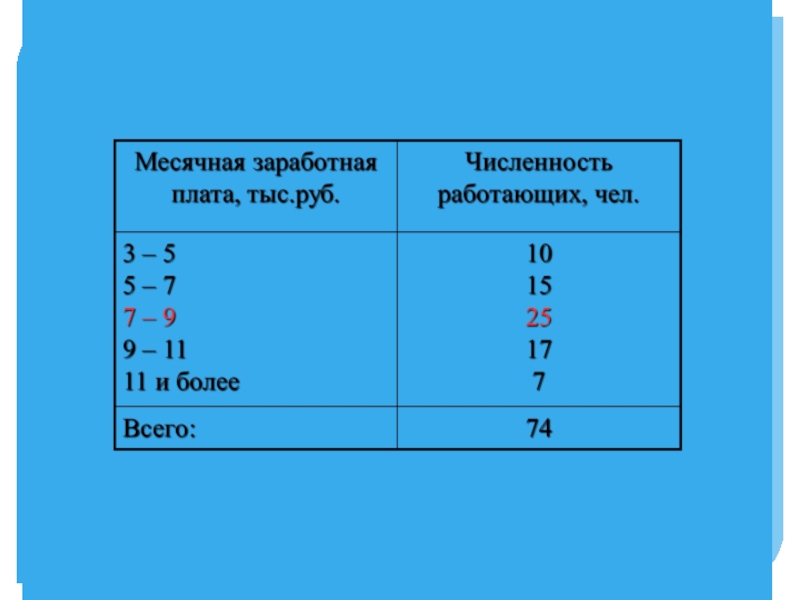
Слайд 422. Если исходные данные представлены в виде дискретного вариационного ряда распределения,
то
медианным называется значение, у которого накопленная частота первой превысит половину суммы частот
медианным называется значение, у которого накопленная частота первой превысит половину суммы частот
Слайд 49Если исходные данные не сгруппированы и представлены в виде числовой последовательности,
то первой квартилей будет называться значение отделяющие ¼ упорядоченной совокупности. Третей квартилей будет называться значение признака отделяющее ¾ упорядоченной совокупности.
Слайд 502. Если исходные данные представлены в виде дискретного вариационного ряда распределения,
то
Первым квартильным называется значение, у которого накопленная частота первой превысит ¼ суммы частот.
Третим квартильным называется значение, у которого накопленная частота первой превысит ¾ суммы частот.
Первым квартильным называется значение, у которого накопленная частота первой превысит ¼ суммы частот.
Третим квартильным называется значение, у которого накопленная частота первой превысит ¾ суммы частот.