- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение технологии Cilk для решения СЛАУ презентация
Содержание
- 1. Применение технологии Cilk для решения СЛАУ
- 2. Содержание Постановка задачи Разложение Холецкого Обратный ход
- 3. Рассмотрим систему из n линейных алгебраических уравнений
- 4. Разложение Холецкого Разложение Холецкого – представление матрицы
- 5. Последовательный алгоритм Элементы матрицы L вычисляются по
- 6. Обратный ход Ly=b, LTx=y Решение этих систем
- 7. Трудоемкость Общее время работы метода оценивается кубической
- 8. Оценка эффективности На практике часто необходимо решить:
- 9. Блочный алгоритм Применение технологии Cilk для решения
- 10. Блочный алгоритм Фактор матрицы A вычисляется
- 11. Параллельный алгоритм В основу положен принцип распараллеливания
- 12. Вычисление диагонального элемента L Распараллеливание: Применение технологии Cilk для решения СЛАУ , где
- 13. Вычисление элементов i-ой строки , если j
- 14. Блочное умножение где Пусть дано блочное
- 15. Выполнение матричного умножения Распараллеливание: -
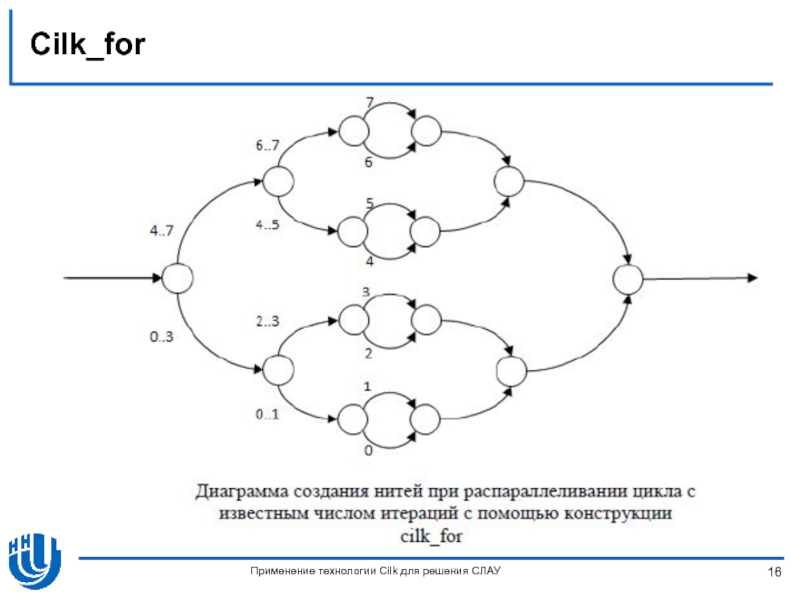
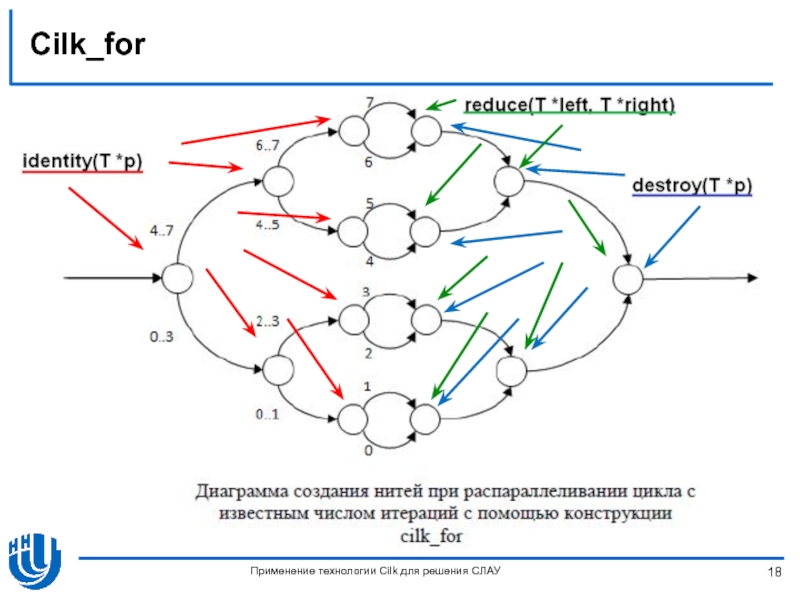
- 16. Сilk_for Применение технологии Cilk для решения СЛАУ
- 17. Reducer Класс Monoid, реализующий моноид, для работы
- 18. Сilk_for Применение технологии Cilk для решения СЛАУ
- 19. Reducer Базовый тип, определяющий необходимые параметры для
- 20. Reducer Реализация функции reduce (T *left, T *right) Применение технологии Cilk для решения СЛАУ
- 21. Reducer Класс – оболочка, для упрощенной работы
- 22. Reducer Объявление и начальная инициализация редьюсера: reducerAddMatrix C(size, A); Применение технологии Cilk для решения СЛАУ
- 23. Reducer Реализация функции Op (): Применение технологии Cilk для решения СЛАУ
- 24. Reducer Использование редьюсера на примере нахождения диагонального
- 25. Результаты экспериментов Применение технологии Cilk для решения СЛАУ
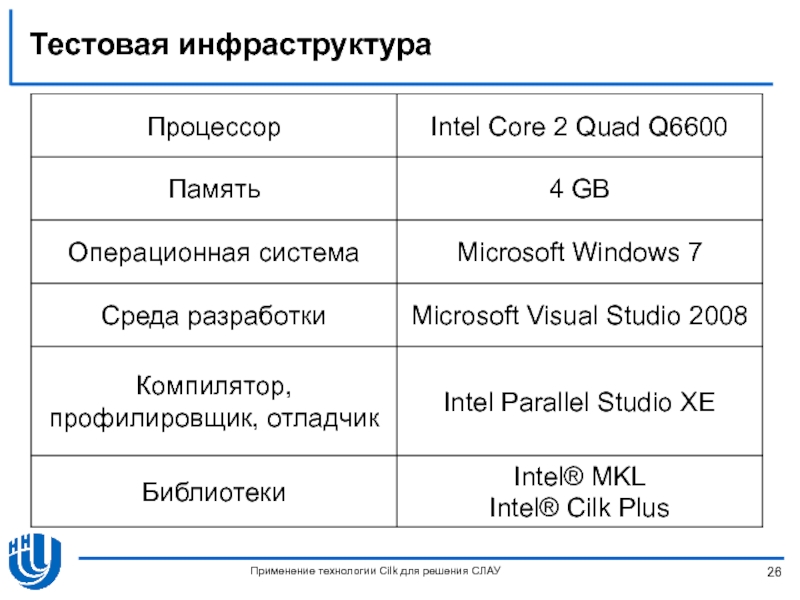
- 26. Тестовая инфраструктура Применение технологии Cilk для решения СЛАУ
- 27. Методы тестирования программной реализации Анализ
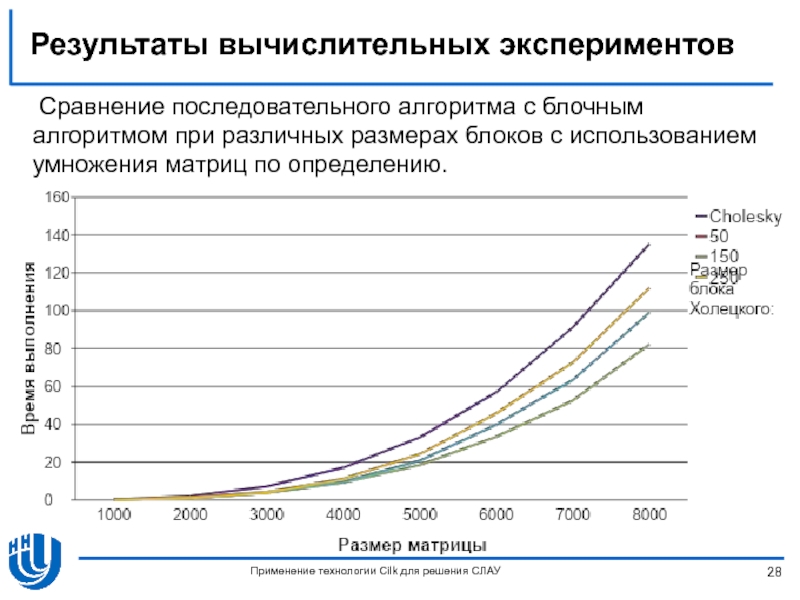
- 28. Результаты вычислительных экспериментов Применение технологии Cilk для
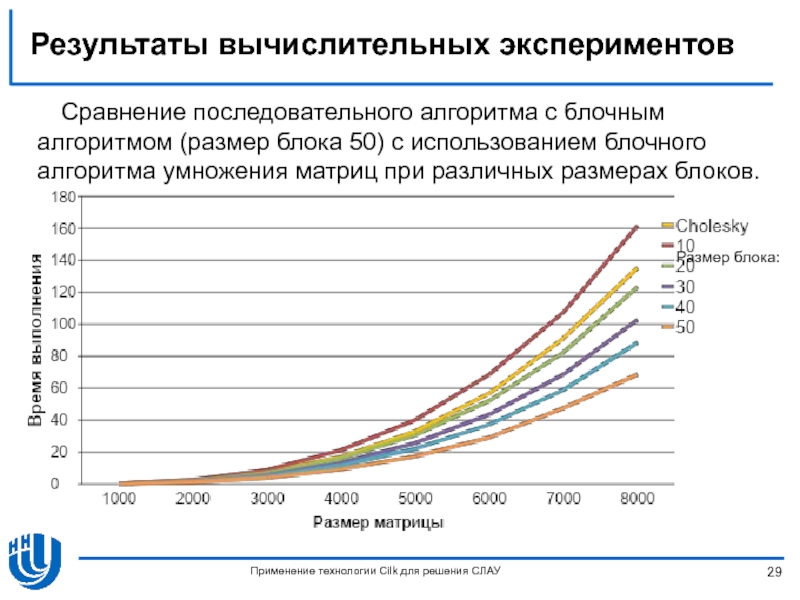
- 29. Результаты вычислительных экспериментов Применение технологии Cilk для
- 30. Результаты вычислительных экспериментов Применение технологии Cilk для
- 31. Результаты вычислительных экспериментов Применение технологии Cilk для
- 32. Заключение Применение технологии Cilk для решения СЛАУ
- 33. Вопросы ? Применение технологии Cilk для решения СЛАУ
Слайд 1Применение технологии Cilk для решения СЛАУ
Параллельные численные методы
Кутилов Е., Генералова Е.
Слайд 2Содержание
Постановка задачи
Разложение Холецкого
Обратный ход
Трудоемкость
Оценка эффективности
Блочный алгоритм
Параллельный алгоритм
Результаты вычислительных экспериментов
Заключение
Применение технологии Cilk
Слайд 3Рассмотрим систему из n линейных алгебраических уравнений вида:
В матричном виде:
А -
b, x - вектора размерности n.
Постановка задачи
Применение технологии Cilk для решения СЛАУ
Слайд 4Разложение Холецкого
Разложение Холецкого – представление матрицы A в виде A =
Необходимое условие:
Матрица A – симметричная:
Матрица А - положительно-определённая:
Применение технологии Cilk для решения СЛАУ
Слайд 5Последовательный алгоритм
Элементы матрицы L вычисляются по следующим формулам:
, если j < i.
Применение технологии Cilk для решения СЛАУ
Слайд 6Обратный ход
Ly=b, LTx=y
Решение этих систем находится по формулам обратного хода метода
Если разложение получено, то решение системы сводится к последовательному решению двух линейных систем уравнений с треугольными матрицами:
Применение технологии Cilk для решения СЛАУ
Слайд 7Трудоемкость
Общее время работы метода оценивается кубической трудоемкостью O(n3).
Обратный ход оценивается
Применение технологии Cilk для решения СЛАУ
Слайд 8Оценка эффективности
На практике часто необходимо решить: Ax=B,
где B матрица правых
Матрицу A необходимо факторизовать один раз для всех правых частей.
После факторизации решение каждой системы занимает квадратичное время.
Таким образом, трудоемкость становиться близкой к квадратичной (за счет многократного применения обратного хода).
Применение технологии Cilk для решения СЛАУ
Слайд 9Блочный алгоритм
Применение технологии Cilk для решения СЛАУ
Недостаток классического алгоритма – плохая
Избежать это можно использованием блочного алгоритма работы с матрицами.
Это позволяет добиться большей локализации данных, что в дальнейшем поможет в распараллеливании алгоритма.
Слайд 10Блочный алгоритм
Фактор матрицы A вычисляется по формулам:
, если j
Извлечение корня соответствует выполнению разложения Холецкого.
Операция Ljj-1 соответствует нахождению обратной матрицы для Ljj.
Применение технологии Cilk для решения СЛАУ
где q = n / r - количество блоков
Слайд 11Параллельный алгоритм
В основу положен принцип распараллеливания по данным.
Распараллеливание возможно для следующих
вычисление диагонального элемента Lii
вычисление элементов i-ой строки
выполнение матричного умножения
Параллельная версия выполнена с использованием технологии Intel® Cilk Plus.
Применение технологии Cilk для решения СЛАУ
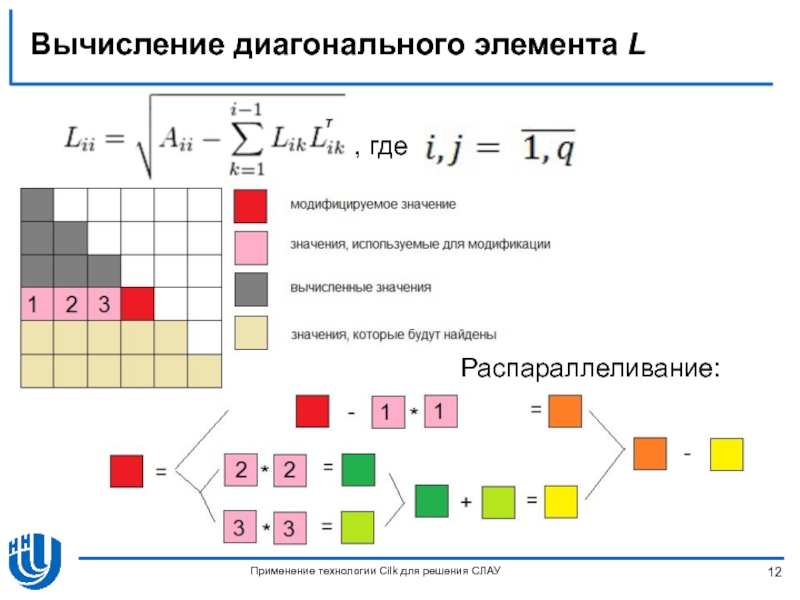
Слайд 12Вычисление диагонального элемента L
Распараллеливание:
Применение технологии Cilk для решения СЛАУ
, где
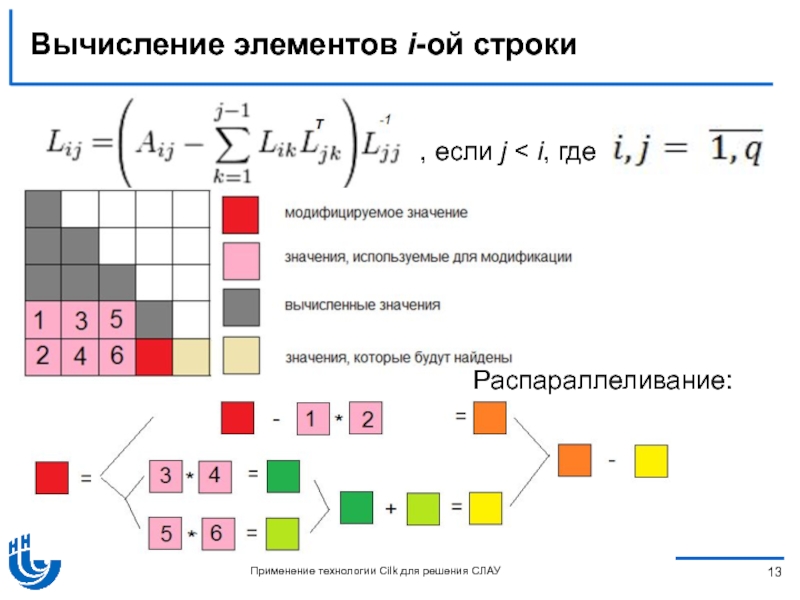
Слайд 13Вычисление элементов i-ой строки
, если j < i, где
Распараллеливание:
Применение
Слайд 14Блочное умножение
где
Пусть дано блочное представление матрицы A и матрицы B,
Применение технологии Cilk для решения СЛАУ
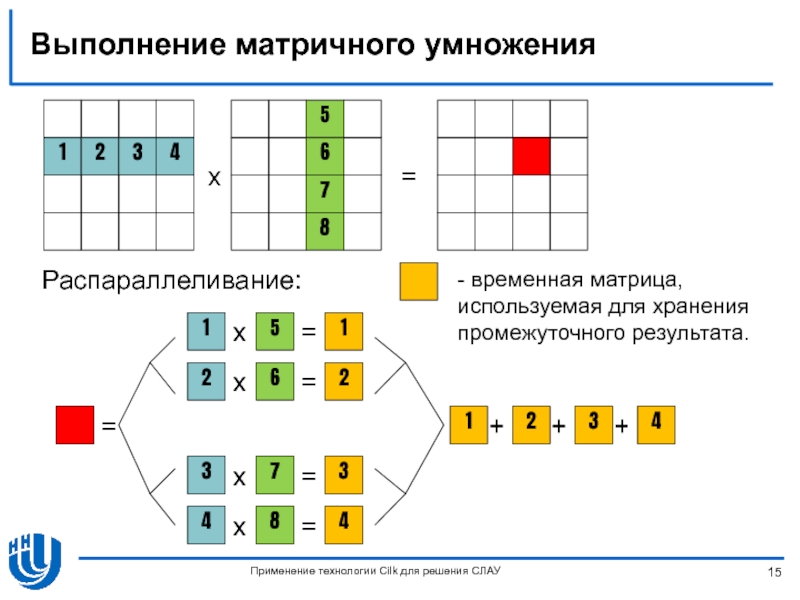
Слайд 15Выполнение матричного умножения
Распараллеливание:
- временная матрица, используемая для хранения промежуточного результата.
Применение
Слайд 17Reducer
Класс Monoid, реализующий моноид, для работы с редьюсером. Этот класс содержит
reduce (T *left, T *right) вычисляет *left = *left OP *right,
identity (T *p) создаёт нейтральный элемент в области памяти, на которую указывает p,
destroy (T *p) вызывает деструктор для объекта, на который указывает p,
Применение технологии Cilk для решения СЛАУ
Слайд 19Reducer
Базовый тип, определяющий необходимые параметры для исходной матрицы, - класс MyStruct.
Применение
Слайд 20Reducer
Реализация функции reduce (T *left, T *right)
Применение технологии Cilk для решения
Слайд 21Reducer
Класс – оболочка, для упрощенной работы с редьюсером, содержит :
cilk::reducer
Методы доступа и изменения:
reducerAddMatrix ( int size_A, double* &A );
void Op ( int sizeBlock, int startIndexA,
int numberRowsA, int numberColumnsA, double* temp_A );
Применение технологии Cilk для решения СЛАУ
Слайд 22Reducer
Объявление и начальная инициализация редьюсера:
reducerAddMatrix C(size, A);
Применение технологии Cilk для решения
Слайд 24Reducer
Использование редьюсера на примере нахождения диагонального элемента матрицы L:
Применение технологии Cilk
Слайд 27Методы тестирования
программной реализации
Анализ корректности разработанной программной реализации разложения Холецкого
Оценкой производительности является общее время решения поставленной задачи.
Применение технологии Cilk для решения СЛАУ
Слайд 28Результаты вычислительных экспериментов
Применение технологии Cilk для решения СЛАУ
Сравнение последовательного алгоритма
Слайд 29Результаты вычислительных экспериментов
Применение технологии Cilk для решения СЛАУ
Сравнение последовательного алгоритма
Размер блока:
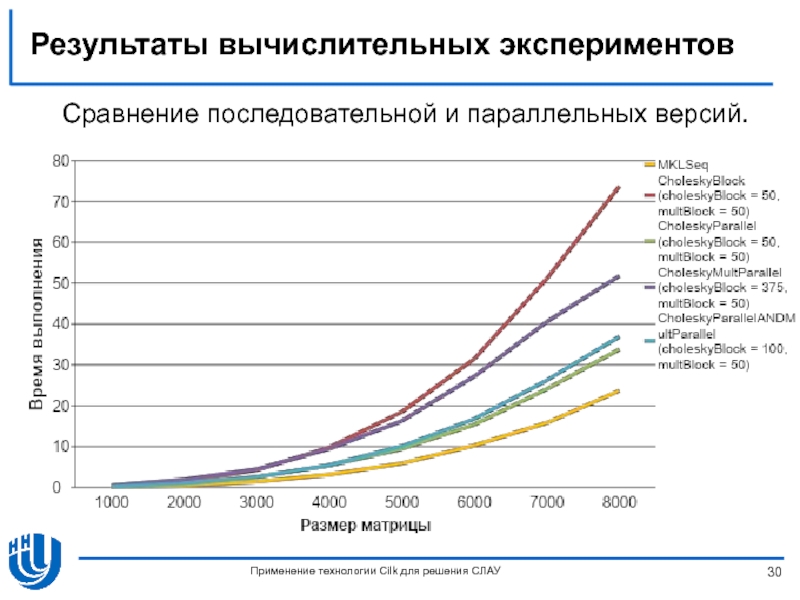
Слайд 30Результаты вычислительных экспериментов
Применение технологии Cilk для решения СЛАУ
Сравнение последовательной и
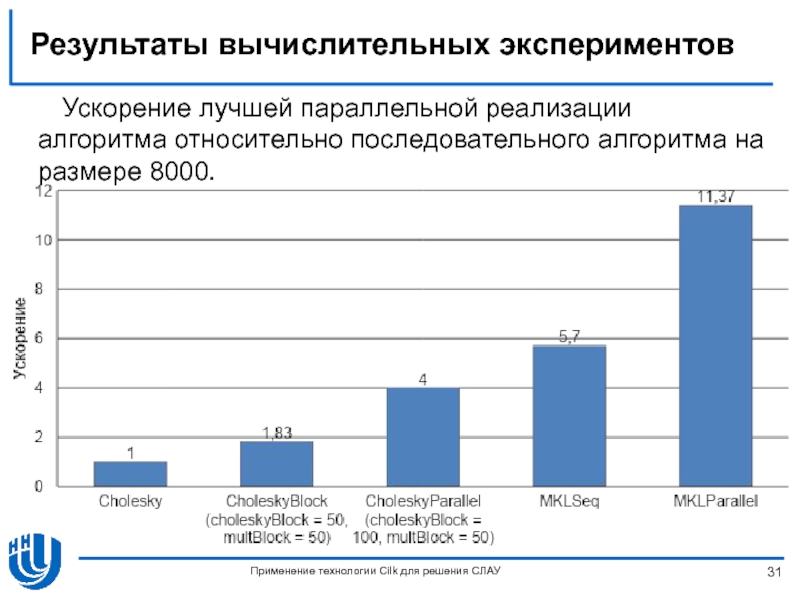
Слайд 31Результаты вычислительных экспериментов
Применение технологии Cilk для решения СЛАУ
Ускорение лучшей параллельной
Слайд 32Заключение
Применение технологии Cilk для решения СЛАУ
В ходе работы изучены расширенные
Реализовано несколько программных модификаций алгоритма разложения Холецкого.
Для параллельной модификации алгоритма Холецкого разработаны собственные редьюсеры.
Наиболее эффективная реализация алгоритма показала отставание от MKL в 3 раза.