- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Педагогическая технология - это такое построение деятельности учителя, в котором входящие в него действия представлены в определенной последовательности и предполагают достижения прогнозируемого результата. презентация
Содержание
- 1. Педагогическая технология - это такое построение деятельности учителя, в котором входящие в него действия представлены в определенной последовательности и предполагают достижения прогнозируемого результата.
- 2. Педагогическая технология отвечает на вопрос:
- 3. ПЕДАГОГИЧЕСКИЕ ТЕХНОЛОГИИ О Р И Е
- 4. технологию дистанционного обучения Идивидуализация обучения технологию модульного
- 5. Активные методы обучения методы обучения,
- 6. Деятельность учителя мотивирует управляет организует создает
- 7. технологии учебного процесса Проблемное
- 8. Проблемное обучение Суть проблемной интерпретации учебного материала
- 9. отбор актуальных, сущностных задач; определение
- 10. Задачи научно - исследовательской работы
- 11. В формировании исследовательской компетенции можно выделить три
- 12. • мотивация исследовательской
- 13. создание установки на необходимость использования математического моделирования;
- 14. этапы математического моделирования Построение модели Решение
- 15. средства достижения прикладной и практической направленности обучения
- 16. Особенностям учащихся, которые следует учитывать при
- 17. Преимущества модульной технологии Идея активности
- 18. Цели применения ИКТ в образовании 1. Поддержка
- 19. Целесообразность применения ИТ диагностическое тестирование качества усвоения
- 20. Проблемное обучение Тема «Теорема Пифагора».
- 21. Исследовательские работы. 9 класс.
- 22. Задание требующее составления математической модели по анализируемому
Слайд 1
Плохой учитель преподносит истину, хороший – учит ее находить.
А. Дистервег
«Педагогическая технология»
Слайд 2Педагогическая технология отвечает
на вопрос:
КАК УЧИТЬ РЕЗУЛЬТАТИВНО?
сущность педагогической технологии:
однозначное и
отбор и структура содержания (что);
оптимальная организация учебного процесса (как);
методы, приемы и средства обучения (с помощью чего);
а так же учет необходимого реального уровня квалификации учителя (кто);
и объективные методы оценки результатов обучения (так ли это).
Слайд 3ПЕДАГОГИЧЕСКИЕ ТЕХНОЛОГИИ
О
Р
И
Е
Н
Т
И
Р
О
В
А
Н
формирование положительной мотивации к учебному труду,
интенсификацию коммуникативной среды,
развитие личности, способной
охрану здоровья учащихся
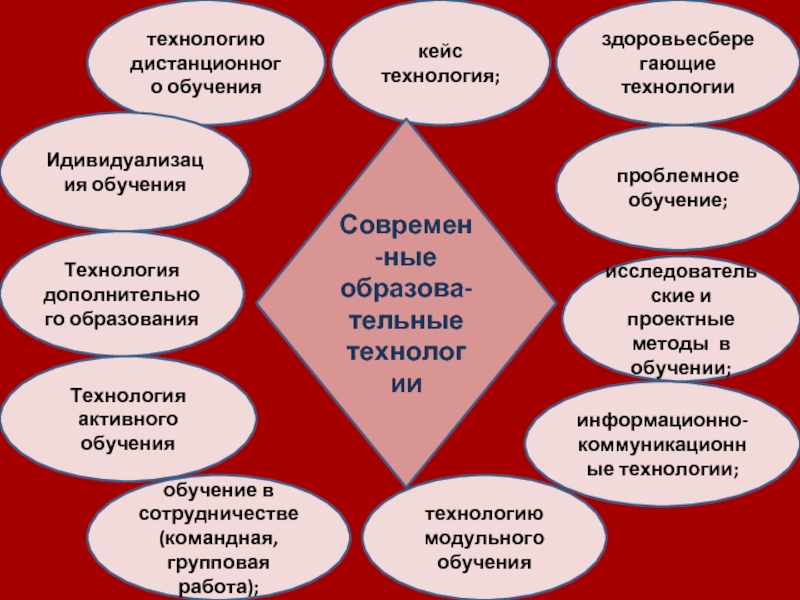
Слайд 4технологию дистанционного обучения
Идивидуализация обучения
технологию модульного обучения
информационно-коммуникационные технологии;
исследовательские и проектные методы в
проблемное обучение;
здоровьесберегающие технологии
Технология дополнительного образования
Технология активного обучения
обучение в сотрудничестве (командная, групповая работа);
кейс технология;
Современ-ные образова-тельные технологии
Слайд 5Активные методы обучения
методы обучения, при которых деятельность
методы, стимулирующие познавательную деятельность обучающегося и строящегося на диалогах, предполагающих свободный обмен мнениями о путях разрешения той или иной проблемы (Мирежиков В.А.).
Интерактивные* методы обучения - специальная форма организации познавательной деятельности, направленная на диалоговое обучение, в ходе которого осуществляется взаимодействие.
*Интерактивный - способный действовать или находиться в режиме диалога, беседы.
Слайд 7 технологии учебного процесса
Проблемное обучение
ТРИЗ (технология решения исследовательских задач)
Математическое
Прикладной и практический характер обучения
Модульная технология
Индивидуализация обучения.
Слайд 8Проблемное обучение
Суть проблемной интерпретации учебного материала состоит в том, что учитель
В результате последовательного и целенаправленного выдвижения познавательных задач и последовательного их разрешения, обучающие активно усваивают знания, развивая при этом познавательную активность и творческую самостоятельность.
Слайд 9 отбор актуальных, сущностных задач;
определение особенностей проблемного обучения в различных
построение оптимальной системы проблемного обучения, создание учебных и методических пособий и рекомендаций;
личностный подход и мастерство учителя.
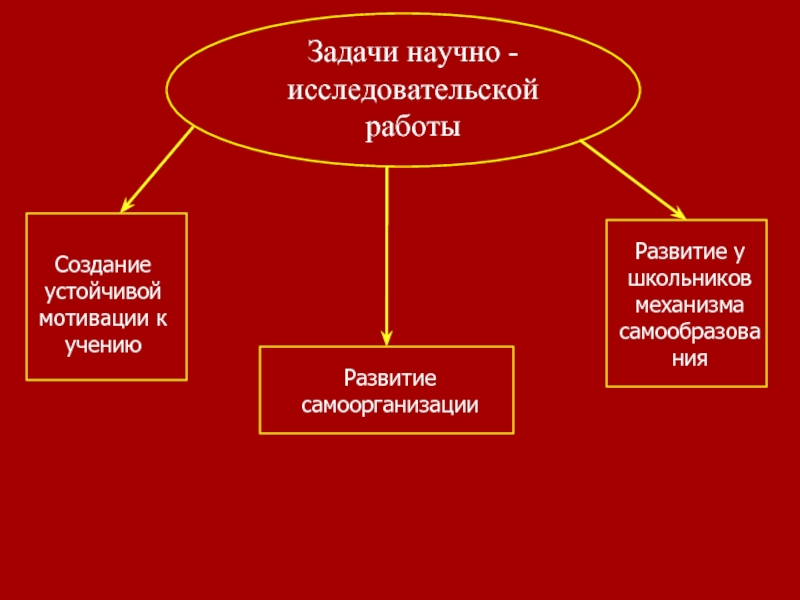
Слайд 10Задачи научно - исследовательской работы
Создание устойчивой мотивации к учению
Развитие самоорганизации
Развитие у
Слайд 11В формировании исследовательской компетенции можно выделить три этапа
Подготовительный
Развивающий 7 – 9 классы
Развитие творческих способностей. Формирование основ исследовательской деятельности
Завершающий 10 – 11 классы
Развитие умений и навыков исследовательской деятельности
Слайд 12• мотивация исследовательской деятельности; • постановка
Слайд 13создание установки на необходимость использования математического моделирования;
формирование математической модели;
исследование
последовательность работы по формированию математических моделей на уроках:
Слайд 14этапы математического моделирования
Построение модели
Решение математической задачи, к которой приводит модель
Интерпретация
Проверка адекватности модели
Модификация модели
Слайд 15средства достижения прикладной и практической направленности обучения математике
планомерное развитие у
построения и чтения графиков,
составления и применения таблиц,
пользования справочной литературой
Слайд 16
Особенностям учащихся, которые следует учитывать при индивидуализации учебной работы:
уровень умственного развития
индивидуально-типологические особенности;
познавательные интересы (на фоне общей учебной мотивации);
скорость прохождения и понимания учебных предметов: быстро, медленно.
Слайд 17
Преимущества модульной технологии
Идея активности ученика на основе:
самоконтроля
индивидуализированный темп учебно –
Ориентировочная основа деятельности
Гибкое управление, переходящее в самоуправление
Рефлективный подход
Слайд 18Цели применения ИКТ в образовании
1. Поддержка и развитие системности мышления обучаемого;
2.
3. Реализация принципа индивидуализации учебного процесса при сохранении его целостности.
Слайд 19Целесообразность применения ИТ
диагностическое тестирование качества усвоения учебного материала;
в тренировочном режиме
в обучающем режиме;
при работе с отстающими учениками;
в режиме самообучения;
в режиме графической иллюстрации изучаемого материала.
Слайд 20Проблемное обучение
Тема «Теорема Пифагора».
На охоте с двух отвесных скал два охотника
Тема «Пропорциональность отрезков хорд и секущих окружности».
Проблемная задача. Как далеко видно из самолета, летящего на высоте 4 км над Землей, если радиус Земли 6370км?
Тема « Сумма n первых членов арифметической прогрессии».
Для создания проблемной ситуации учащимся предлагается старинная задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками, разность же между каждым человеком и его соседом равняется 1/8 меры».
Слайд 21Исследовательские работы.
9 класс. Квадратичная функция.
Дана
При каких а уравнение f (x, a) = 0 (относительно х) имеет хотя бы один вещественный корень?
Вычислите сумму квадратов s(a) корней многочлена f (x, a) как функцию от параметра а.
При каком а сумма s(a) квадратов вещественных корней многочлена f (x, a) принимает наименьшее значение?
При каждом фиксированном значении параметра а вычислите наименьшее значение m=m(a) квадратичной функции у = f (x, a).
Определите, при каких а областью значений функции у = f (x, a) является промежуток [3; +∞).
Найдите наибольшее значение функции m=m(a).
При каких а многочлен f (x, a) имеет два положительных корня?
Из уравнения f (x, a) = 0 выразите а как функцию от х.
При больших (по модулю) значениях х значение функции а = а(х) близки к значениям некоторой линейной функции. Найдите эту функцию.
С помощью графика функции а = а(х) определите, при каких а неравенство f (x, a)≤ 0 верно при всех х из промежутка [1; 4]
Слайд 22Задание требующее составления математической модели по анализируемому тексту.
Например, в теме «Прямая
Кому многое дано,
С того многое взыщется. (Евангелие от Луки)
Чтоб более меня читали,
Я стану менее писать. (П. Вяземский)