- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы поиска в структурированных файлах презентация
Содержание
- 1. Методы поиска в структурированных файлах
- 2. Содержание Векторная модель TF-IDF Косинусная мера Структурированный
- 3. Векторная модель Векторная модель (англ. vector space
- 4. Векторная модель Более формально dj =
- 5. TF-IDF TF-IDF (от англ. TF — term
- 6. Косинусная мера
- 7. Косинусная мера
- 8. Структурированный файл на примере XML* Shakespeare
- 9. Лексические поддеревья Деревья, содержащие хотя бы один словарный терм
- 10. Лексические поддеревья С увеличением количества узлов в дереве растет число лексических поддеревьев.
- 11. Структурные термы Будем рассматривать только такие лексические
- 12. Расширение векторной модели на случай структурированных файлов
- 13. Схожесть контекстов 1 способ
- 14. Схожесть контекстов 2 способ Рассмотрим запрос в
- 15. Схожесть контекстов LCS(Q,A) Longest Common Subsequence
- 16. Критерии оценки Контекст А включает
- 17. Схожесть контекстов POS(Q,A) POS(Q,A) =
- 18. Схожесть контекстов GAPS(Q,A) GAPS(Q,A) =
- 19. Схожесть контекстов LD(Q,A) LD(Q,A)= (|A|-
- 20. Схожесть контекстов cr(Q,A) = αLCS(Q,A)
- 21. Примеры Показывают, как влияют оценки LCS(Q,A) ,
- 22. Пример A1. Влияние lcs(Q,A) на cr(Q,A) Пример A2. Влияние AP(Q,A) на cr(Q,A)
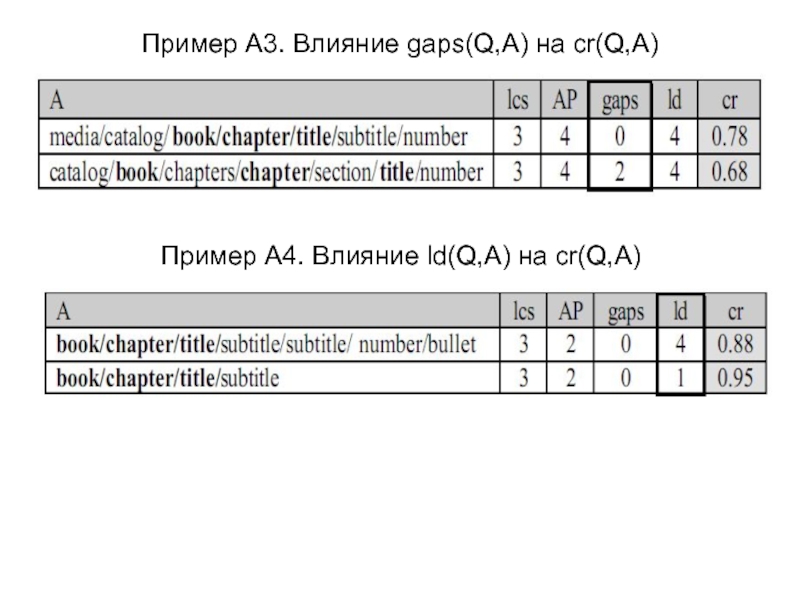
- 23. Пример A3. Влияние gaps(Q,A) на cr(Q,A) Пример A4. Влияние ld(Q,A) на cr(Q,A)
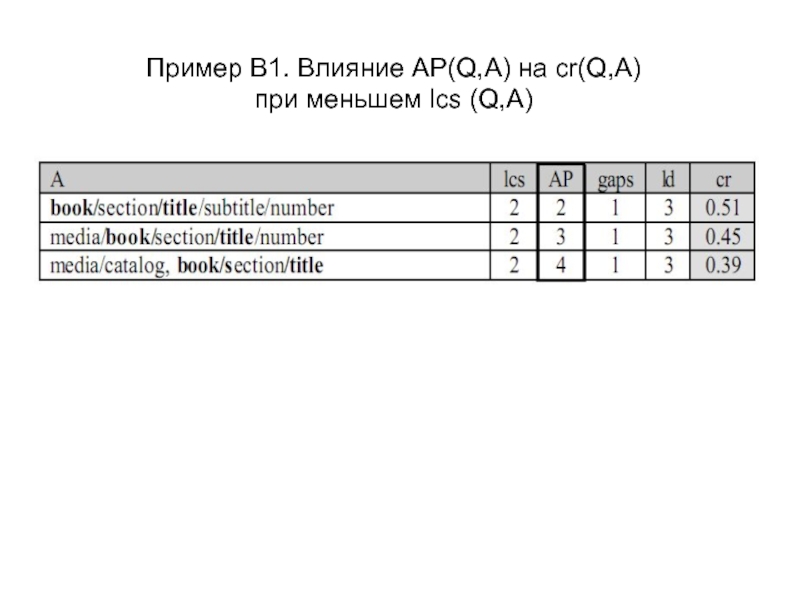
- 24. Пример B1. Влияние AP(Q,A) на cr(Q,A) при меньшем lcs (Q,A)
- 25. Okapi BM25 d -
- 26. Okapi BM25
- 27. BM25F модификация BM25, в которой документ рассматривается
- 28. BM25F Пусть имеется nF полей f =
- 29. BM25F Пусть имеется nF полей f =
- 30. BM25F Если считать, что полю f присвоен
- 31. BM25E В BM25F вместо частоты терма в
- 32. BM25E Пусть имеется nЕ элементов е =
- 33. ВМ25Е Соответственно, функция ВМ25Е:
- 34. BM25E Соответственно,
- 35. Литература Christopher D. Manning, Prabhakar Raghavan and
- 36. Спасибо за внимание!
Слайд 2Содержание
Векторная модель
TF-IDF
Косинусная мера
Структурированный файл
на примере XML
Лексические поддеревья
Структурные термы
Расширение векторной модели на
случай структурированных файлов
Схожесть контекстов
Okapi BM25
BM25F
BM25Е
Схожесть контекстов
Okapi BM25
BM25F
BM25Е
Слайд 3Векторная модель
Векторная модель (англ. vector space model) — представление коллекции документов
векторами из одного общего для всей коллекции векторного пространства.
Коллекция - неупорядоченное множество документов.
Документ - неупорядоченное множество термов.
Термы (словарные термы) - слова, из которых состоит текст (определение терма зависит от приложения)
В векторной модели термы – это измерения.
Вес терма – координата в данном измерении.
Коллекция - неупорядоченное множество документов.
Документ - неупорядоченное множество термов.
Термы (словарные термы) - слова, из которых состоит текст (определение терма зависит от приложения)
В векторной модели термы – это измерения.
Вес терма – координата в данном измерении.
Слайд 4Векторная модель
Более формально
dj = (w1j, w2j, …, wnj), где
dj —
векторное представление j-го документа,
wij — вес i-го терма в j-м документе,
n — общее количество различных термов во всех документах коллекции.
Запросы представляются в той же форме, что и документы. Т.е.
q = (w1q,w2q,...,wtq), где
q – векторное представление запроса,
wiq - вес i-го терма в запросе
wij — вес i-го терма в j-м документе,
n — общее количество различных термов во всех документах коллекции.
Запросы представляются в той же форме, что и документы. Т.е.
q = (w1q,w2q,...,wtq), где
q – векторное представление запроса,
wiq - вес i-го терма в запросе
Слайд 5TF-IDF
TF-IDF (от англ. TF — term frequency, IDF — inverse document
frequency) — статистическая мера, используемая для оценки важности слова в контексте документа, являющегося частью коллекции документов. TF-IDF = TF*IDF
ni - число вхождений терма в документ
k – общее число термов в документе
|D| — количество документов в коллекции
— количество документов, в которых встречается терм ti (когда ni≠0)
ni - число вхождений терма в документ
k – общее число термов в документе
|D| — количество документов в коллекции
— количество документов, в которых встречается терм ti (когда ni≠0)
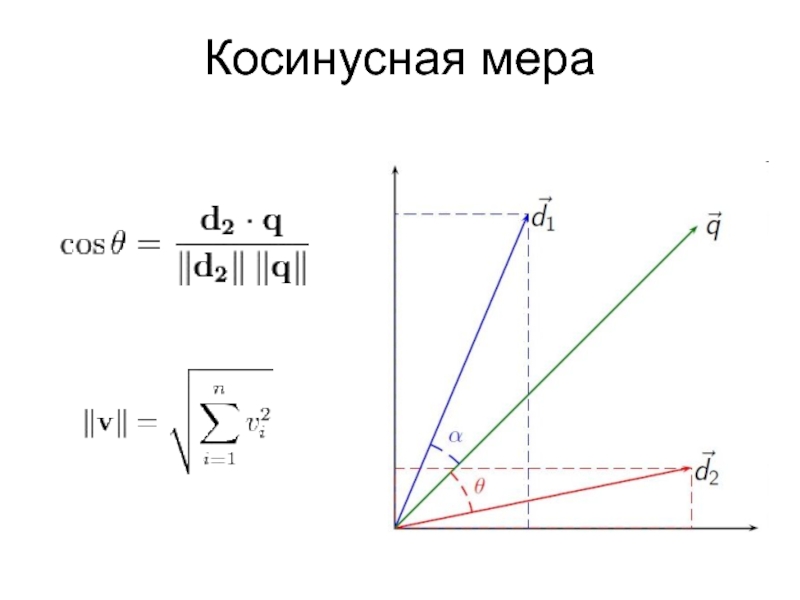
Слайд 7Косинусная мера
ρ(Q,D) – соответствие запроса Q документу D
ti – терм (измерение)
wQ(ti) – вес терма ti в запросе Q
wD(ti) – вес терма ti в документе D
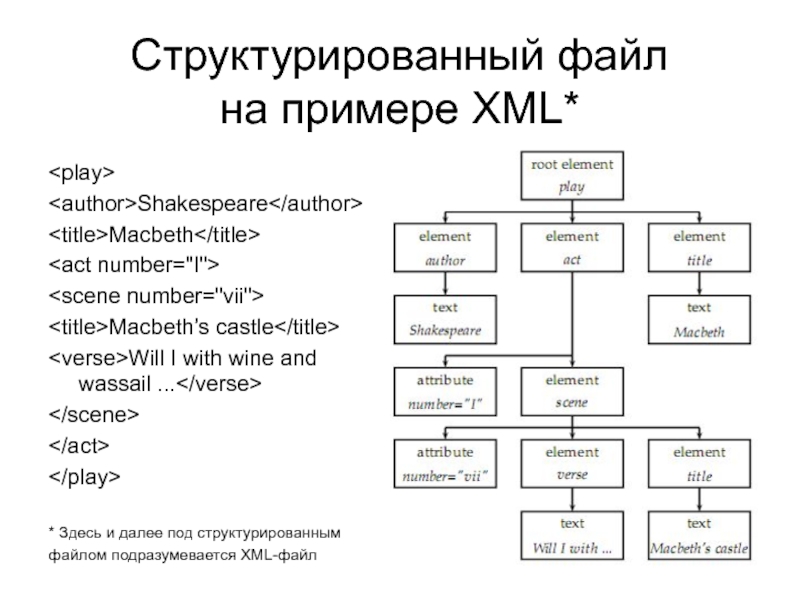
Слайд 8Структурированный файл
на примере XML*
Shakespeare
Macbeth
Macbeth’s castle
Will I with wine and
wassail ...
* Здесь и далее под структурированным
файлом подразумевается XML-файл
* Здесь и далее под структурированным
файлом подразумевается XML-файл
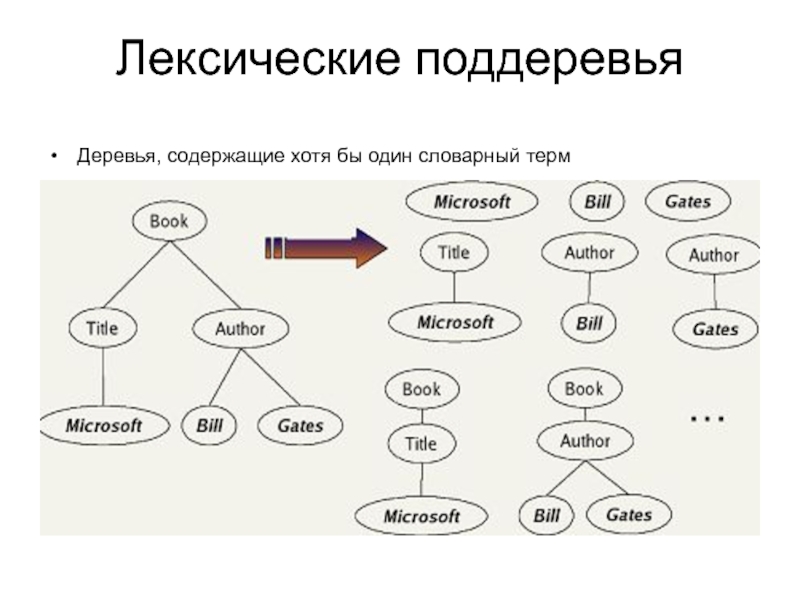
Слайд 10Лексические поддеревья
С увеличением количества узлов в дереве
растет число лексических поддеревьев.
Слайд 11Структурные термы
Будем рассматривать только такие лексические поддеревья, которые оканчиваются единственным словарным
термом
Такие поддеревья называются структурными термами и обозначаются парой (t,c), где t – это терм, c - его XML-контекст.
Такие поддеревья называются структурными термами и обозначаются парой (t,c), где t – это терм, c - его XML-контекст.
Слайд 12Расширение векторной модели на случай структурированных файлов
ρ(Q,D) – соответствие запроса Q
документу D
(ti,c i) – структурный терм (измерение)
wQ(ti,c i) – вес структурного терма (ti,c i) в запросе Q
wD(ti,c i) – вес структурного терма (ti,c i) в документе D
cr(ci,ck) – схожесть контекстов (context resemblance) ci и ck, 0≤cr(ci,ck) ≤1
(ti,c i) – структурный терм (измерение)
wQ(ti,c i) – вес структурного терма (ti,c i) в запросе Q
wD(ti,c i) – вес структурного терма (ti,c i) в документе D
cr(ci,ck) – схожесть контекстов (context resemblance) ci и ck, 0≤cr(ci,ck) ≤1
Слайд 13Схожесть контекстов
1 способ
|cq| - число узлов в контексте, соответствующем терму
из запроса
|cd| - то же, но для документа
|cd| - то же, но для документа
если cq соответствует cd
иначе
Слайд 14Схожесть контекстов
2 способ
Рассмотрим запрос в форме T
Q = q1q2q3 – контекст
появления Т в запросе
А = а1а2…а8 – контекст появления Т в произвольном XML документе
Пример:
Q = language/book/title
A = language/media/book/chapter/section/subsection/title/number
А = а1а2…а8 – контекст появления Т в произвольном XML документе
Пример:
Q = language/book/title
A = language/media/book/chapter/section/subsection/title/number
Слайд 15Схожесть контекстов
LCS(Q,A)
Longest Common Subsequence
LCS(Q,A) = lcs(Q,A)/|Q|, где
lcs(Q,A) – длина наибольшей
общей подпоследовательности Q и А
0 ≤ LCS(Q,A) ≤ 1
0 ≤ LCS(Q,A) ≤ 1
Слайд 16
Критерии оценки
Контекст А включает больше элементов qi в правильном порядке. (В
примере - 3)
Элементы qi появляются ближе к началу А, чем к концу. (В примере – совпадение q1q2q3 с а1а3а7 предпочтительнее, чем с а1а3а8)
Элементы qi появляются в А ближе друг к другу. (В примере – совпадение q1q2q3 с а2а3а4 предпочтительнее, чем с а1а3а5)
Из двух контекстов документа, одинаково совпадающих с контекстом запроса, выше оценивается тот, который имеет меньшую длину.
Элементы qi появляются ближе к началу А, чем к концу. (В примере – совпадение q1q2q3 с а1а3а7 предпочтительнее, чем с а1а3а8)
Элементы qi появляются в А ближе друг к другу. (В примере – совпадение q1q2q3 с а2а3а4 предпочтительнее, чем с а1а3а5)
Из двух контекстов документа, одинаково совпадающих с контекстом запроса, выше оценивается тот, который имеет меньшую длину.
Слайд 17Схожесть контекстов
POS(Q,A)
POS(Q,A) = 1-((AP-AverOptimalPosition)/(|A|-2*AverOptimalPosition+1))
AverOptimalPosition - среднее положение оптимального совпадения Q
и А (если совпадение начинается с первого элемента и продолжается без пробелов)
АР - фактическое среднее положение совпадения Q и А
0 ≤ POS(Q,A) ≤ 1
(0 – в случае полного несовпадения, 1 – в случае «самого левого»
совпадения)
АР - фактическое среднее положение совпадения Q и А
0 ≤ POS(Q,A) ≤ 1
(0 – в случае полного несовпадения, 1 – в случае «самого левого»
совпадения)
Слайд 18Схожесть контекстов
GAPS(Q,A)
GAPS(Q,A) = gaps/(gaps + lcs(Q,A))
gaps - число «пробелов» (в примере
gaps = 4)
0 ≤ GAPS ≤ 1
( 0 – полное совпадение)
0 ≤ GAPS ≤ 1
( 0 – полное совпадение)
Слайд 20Схожесть контекстов
cr(Q,A) = αLCS(Q,A) + βPOS(Q,A) – γGAPS(Q,A) – δLD(Q,A)
0
≤ α ≤ 1, 0 ≤ β ≤ 1, 0 ≤ γ ≤ 1, 0 ≤ δ ≤ 1
α + β = 1 (т.к. cr(Q,A) = 1 в случае полного совпадения)
α + β = 1 (т.к. cr(Q,A) = 1 в случае полного совпадения)
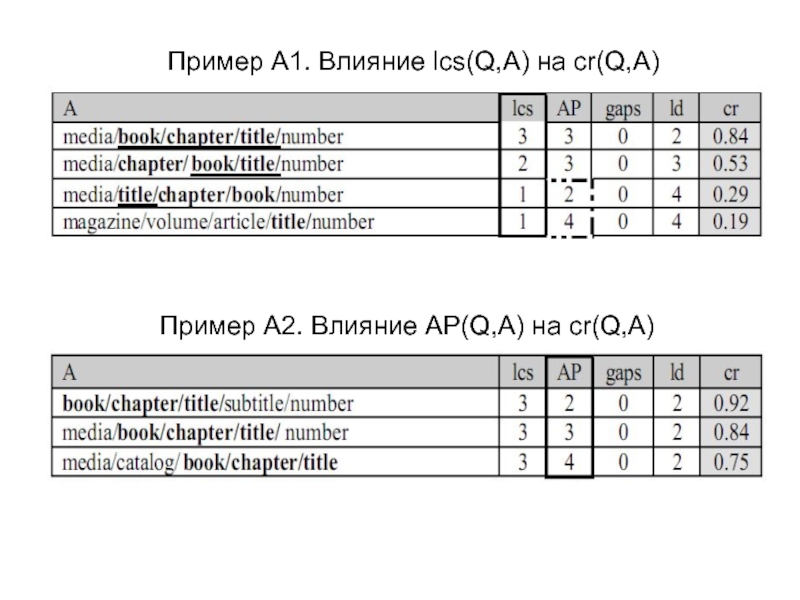
Слайд 21Примеры
Показывают, как влияют оценки LCS(Q,A) , POS(Q,A), GAPS(Q,A), LD(Q,A) на cr(Q,A)
Q = q1q2q3 = book/chapter/title
Положим α = 0.75, β = 0.25, γ = 0.25, δ = 0.2
Для простоты будем рассматривать lcs(Q,A) вместо LCS(Q,A),
АР вместо POS, gaps вместо GAPS, ld вместо LD
Слайд 25Okapi BM25
d - документ
C – коллекция документов
W(d,q,C) – релевантность документа d
из коллекции С запросу q
wj(d,C) – вес j-го терма в документе d коллекции С
qj – совпадание терма j из документа с термом запроса
wj(d,C) – вес j-го терма в документе d коллекции С
qj – совпадание терма j из документа с термом запроса
Слайд 26Okapi BM25
d - документ
C – коллекция документов
wj(d,C) – вес j-го терма
в документе d коллекции С
tfj – частота j-го терма в документе d коллекции С (TF)
dfj – количество документов коллекции, содержащих j-й терм
dl – длина документа
avdl – средняя длина документов в коллекции
k1, b – коэффициенты (обычно k1 = 2, b = 0.75)
tfj – частота j-го терма в документе d коллекции С (TF)
dfj – количество документов коллекции, содержащих j-й терм
dl – длина документа
avdl – средняя длина документов в коллекции
k1, b – коэффициенты (обычно k1 = 2, b = 0.75)
Слайд 27BM25F
модификация BM25, в которой документ рассматривается как совокупность нескольких полей (таких
как, например, заголовки, основной текст, ссылочный текст), длины которых независимо нормализуются, и каждому из которых может быть назначена своя степень значимости в итоговой функции ранжирования.
tf’j – взвешенная частота j-го терма в документе d
dl’ – взвешенная длина документа
avdl’ – взвешенная средняя длина документа
k’1 – взвешенный параметр
tf’j – взвешенная частота j-го терма в документе d
dl’ – взвешенная длина документа
avdl’ – взвешенная средняя длина документа
k’1 – взвешенный параметр
Слайд 28BM25F
Пусть имеется nF полей f = 1, …, nF
В данном поле
f документа d терм t имеет частоту tfd,t,f
Пусть V – это словарь (набор термов). Тогда
Длина поля f в документе d
Частота терма t в документе d
Пусть V – это словарь (набор термов). Тогда
Длина поля f в документе d
Частота терма t в документе d
Слайд 29BM25F
Пусть имеется nF полей f = 1, …, nF
В данном поле
f документа d терм t имеет частоту tfd,t,f
Пусть V – это словарь (набор термов). Тогда
Длина документа d
Средняя длина документа
Пусть V – это словарь (набор термов). Тогда
Длина документа d
Средняя длина документа
Слайд 30BM25F
Если считать, что полю f присвоен вес wf , получим:
N –
мощность коллекции
atf – средняя частота терма
atf – средняя частота терма
Слайд 31BM25E
В BM25F вместо частоты терма в документе используется линейная комбинация взвешенных
частот терма в полях
Этот метод можно применить к поиску элементов.
Элементы можно обрабатывать так же, как и документы. Но каждый элемент может иметь ещё и дополнительные, унаследованные поля
Этот метод можно применить к поиску элементов.
Элементы можно обрабатывать так же, как и документы. Но каждый элемент может иметь ещё и дополнительные, унаследованные поля
Слайд 32BM25E
Пусть имеется nЕ элементов е = 1, …, nЕ в коллекции
С
В элементе е терм t имеет частоту tfd,t,e
el – длина элемента
avel – средняя длина элемента
Тогда расширение ВМ25 на случай поиска элементов:
В элементе е терм t имеет частоту tfd,t,e
el – длина элемента
avel – средняя длина элемента
Тогда расширение ВМ25 на случай поиска элементов:
Слайд 33ВМ25Е
Соответственно, функция ВМ25Е:
tf’e,j – взвешенная частота j-го терма в элементе е
еl’
– взвешенная длина элемента
avеl’ – взвешенная средняя длина элемента в коллекции
k’1 – взвешенный параметр
avеl’ – взвешенная средняя длина элемента в коллекции
k’1 – взвешенный параметр
Слайд 35Литература
Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze, Introduction to Information
Retrieval, Cambridge University Press. 2008.
David Carmel, Nadav Efraty, Gad M. Landau, Yoelle S. Maarek, Yosi Mass, An Extension of the Vector Space Model for Querying XML Documents via XML Fragments, ACM SIGIR'2002 Workshop on XML and IR, Tampere, Finland , Aug 2002
Wei Lu, Stephen Robertson, Andrew Macfarlane, Advances in XML Information Retrieval and Evaluation (INEX 2005). LNCS 3977, Springer 2006 (pp 161-171).
David Carmel, Nadav Efraty, Gad M. Landau, Yoelle S. Maarek, Yosi Mass, An Extension of the Vector Space Model for Querying XML Documents via XML Fragments, ACM SIGIR'2002 Workshop on XML and IR, Tampere, Finland , Aug 2002
Wei Lu, Stephen Robertson, Andrew Macfarlane, Advances in XML Information Retrieval and Evaluation (INEX 2005). LNCS 3977, Springer 2006 (pp 161-171).