- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Автоматизированное построение математических моделей систем по эквивалентным схемам презентация
Содержание
- 1. Автоматизированное построение математических моделей систем по эквивалентным схемам
- 2. Цель Разработать программное обеспечение автоматизированного построения математических
- 3. Алгоритмы на графах Алгоритм Краскала Алгоритм Краскала
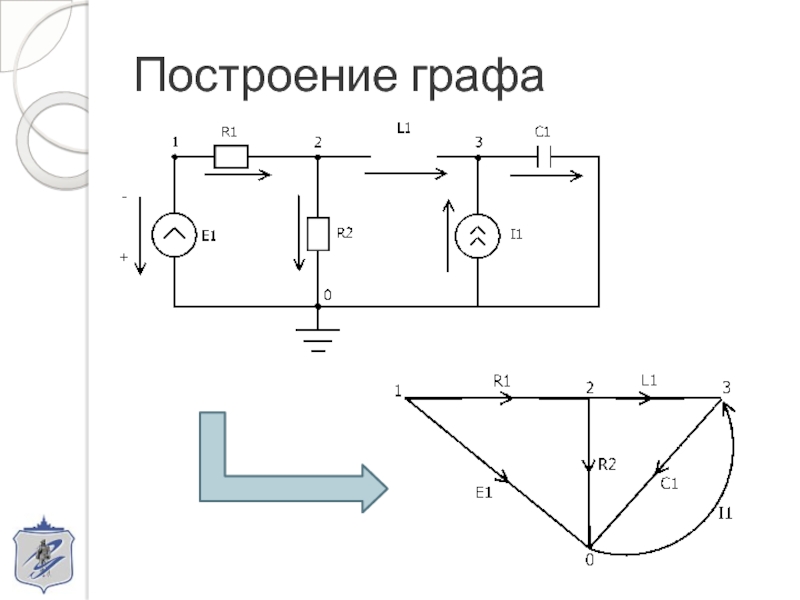
- 4. Построение графа
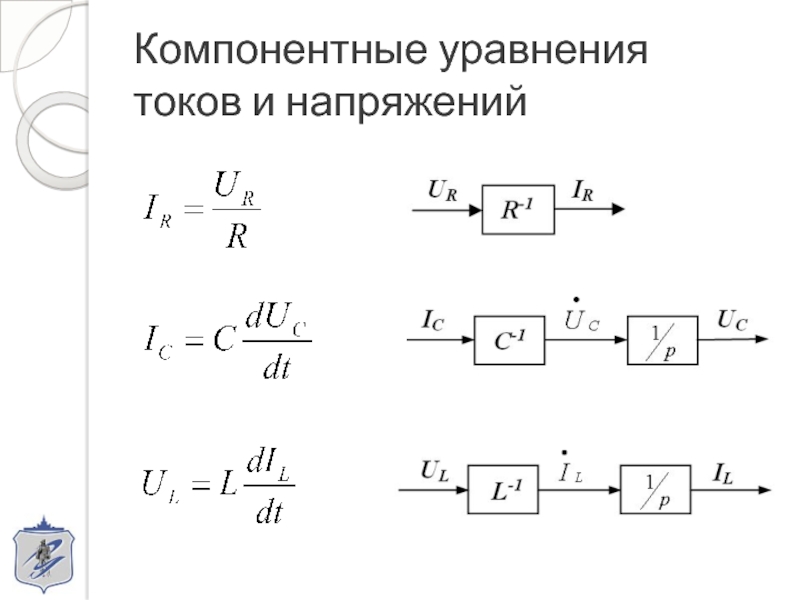
- 5. Компонентные уравнения токов и напряжений
- 6. Топологические уравнения токов и напряжений M = Uх = –M·Uв Iв = MT·Iх
- 7. Матрица «М»
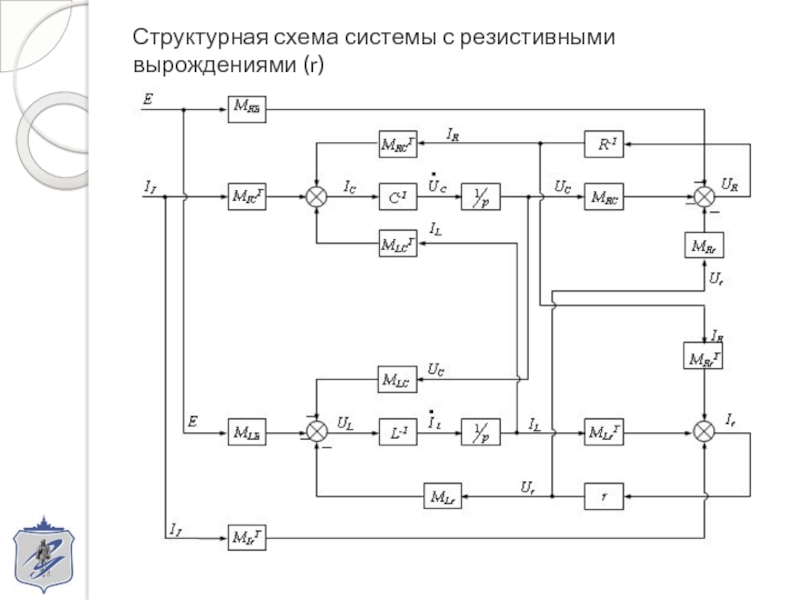
- 8. Структурная схема системы с резистивными вырождениями (r)
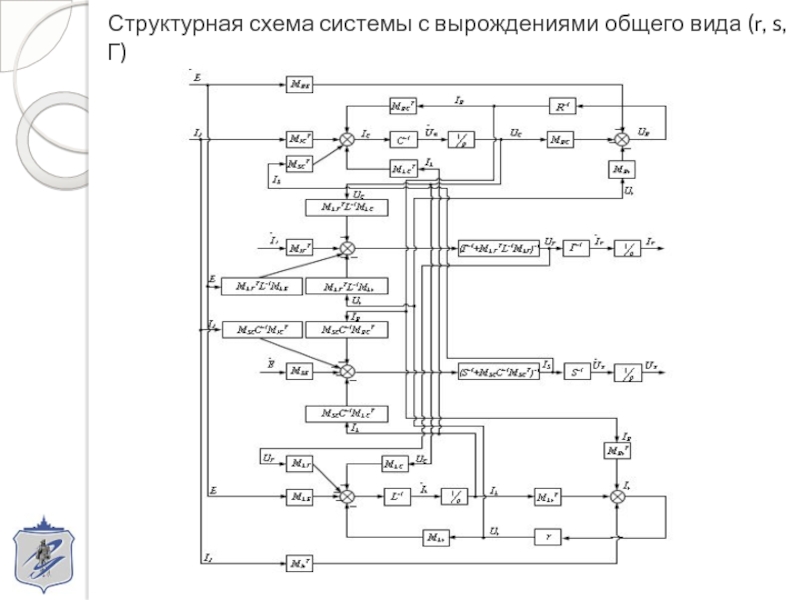
- 9. Структурная схема системы с вырождениями общего вида (r, s, Г)
- 10. Получение математической модели Построение графа по эквивалентной
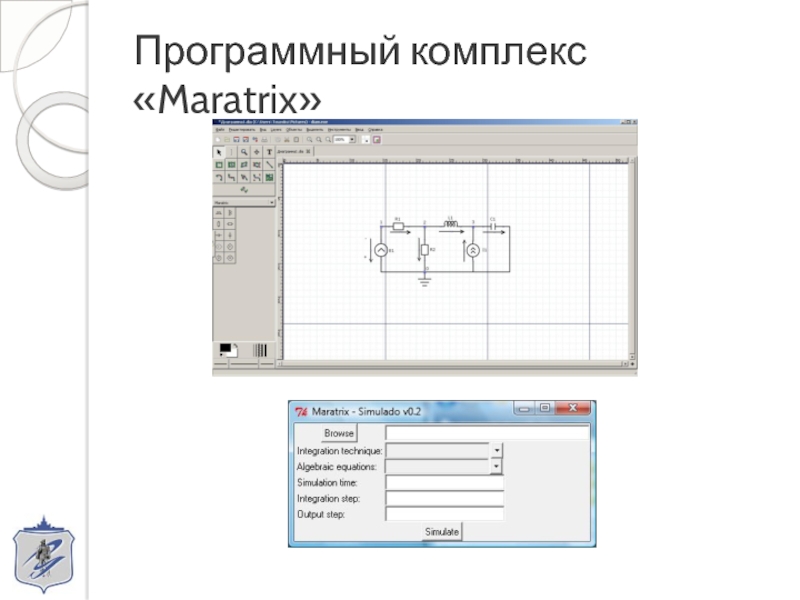
- 11. Программный комплекс «Maratrix»
- 12. Достигнутые результаты Разработано алгоритмическое обеспечение моделирования систем
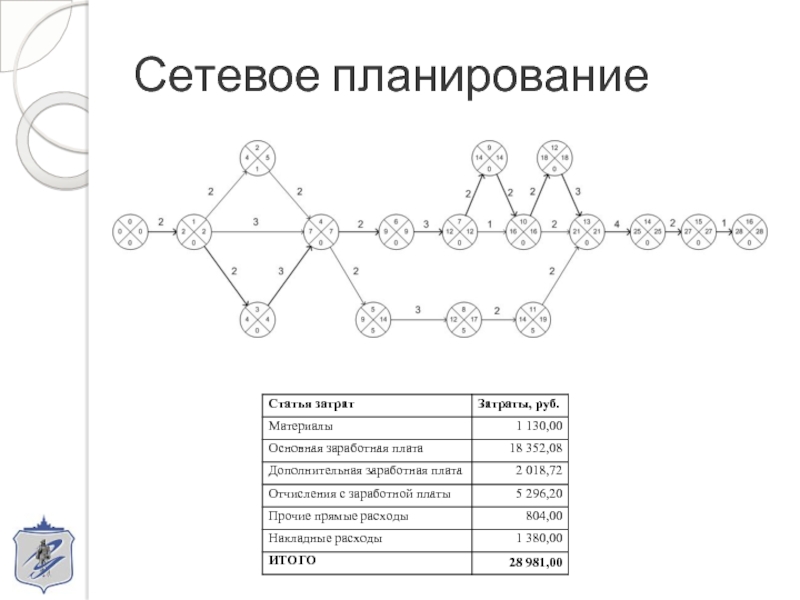
- 13. Сетевое планирование
Слайд 1Автоматизированное построение математических моделей систем по эквивалентным схемам
Вышегородцев М.Е.
Научный руководитель, д.т.н.,
Устюгов М.Н.
Слайд 2Цель
Разработать программное обеспечение автоматизированного построения математических моделей электрических подсистем по эквивалентным
Задачи
Анализ методов и алгоритмов построения фундаментальной матрицы с использованием теории графов
Разработка программного комплекса для решения задач моделирования
Получение и анализ результатов
Слайд 3Алгоритмы на графах
Алгоритм Краскала
Алгоритм Краскала находит остовный лес минимального веса в
Алгоритм Прима
Алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Войцех Ярник (1930), Прим (1961).
Волновой алгоритм
Алгоритм, позволяющий найти минимальный путь в графе с рёбрами единичной длины. Основан на алгоритме поиска в ширину. Применяется для нахождения кратчайшего пути в графе.
Поиск в ширину
Метод обхода и разметки вершин графа
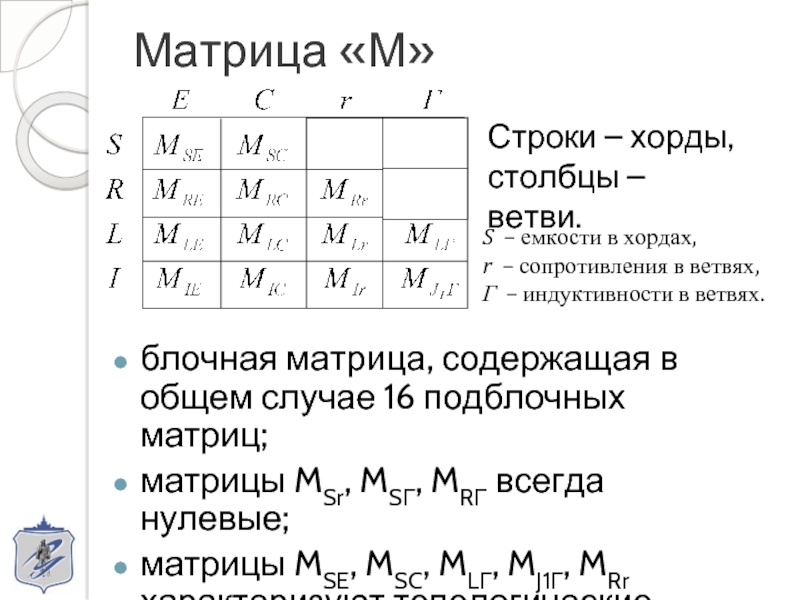
Слайд 7Матрица «М»
,
Строки –
столбцы – ветви.
S – емкости в хордах,
r – сопротивления в ветвях,
Г – индуктивности в ветвях.
блочная матрица, содержащая в общем случае 16 подблочных матриц;
матрицы MSr, MSГ, MRГ всегда нулевые;
матрицы MSE, MSC, MLГ, MJ1Г, MRr характеризуют топологические вырождения.
Слайд 10Получение математической модели
Построение графа по эквивалентной схеме
Выделение минимального остовного дерева и
Получение системы алгебраических и дифференциальных уравнений
Решение системы уравнений численными методами
Слайд 12Достигнутые результаты
Разработано алгоритмическое обеспечение моделирования систем на основе матрицы «М», матрицы
Разработан программный комплекс «Maratrix» для автоматизированного решения задач моделирования
Продолжение работы
Разработать расширения комплекса для моделирования систем различной физической природы, содержащих нелинейные и нестационарные элементы, с учетом взаимовлияния подсистем.