- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
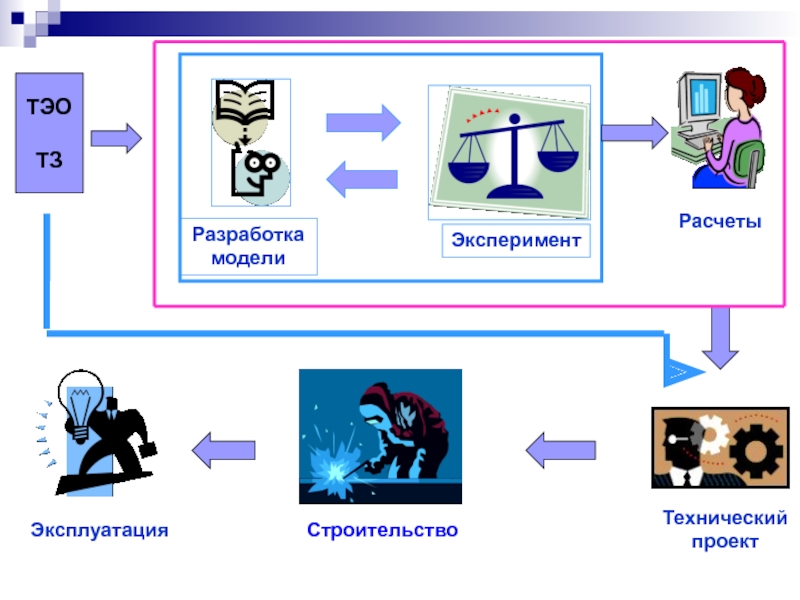
Методы математического моделирования для проектирования защиты пролетов ЛЭП от эоловых вибраций презентация
Содержание
- 1. Методы математического моделирования для проектирования защиты пролетов ЛЭП от эоловых вибраций
- 2. Объект моделирования пролет ЛЭП
- 5. Факторы, учитываемые при моделировании: длина пролета, тяжение
- 6. Провод и спиральная арматура: Модель A
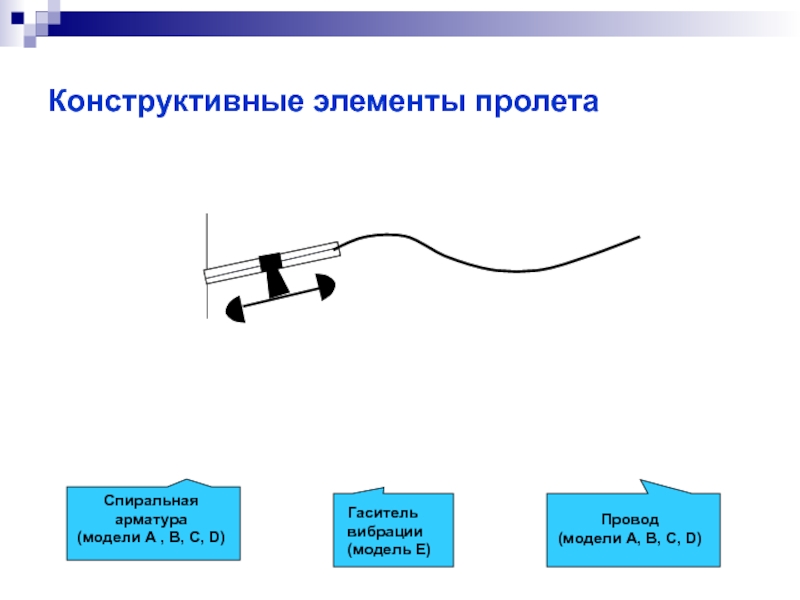
- 7. Конструктивные элементы пролета
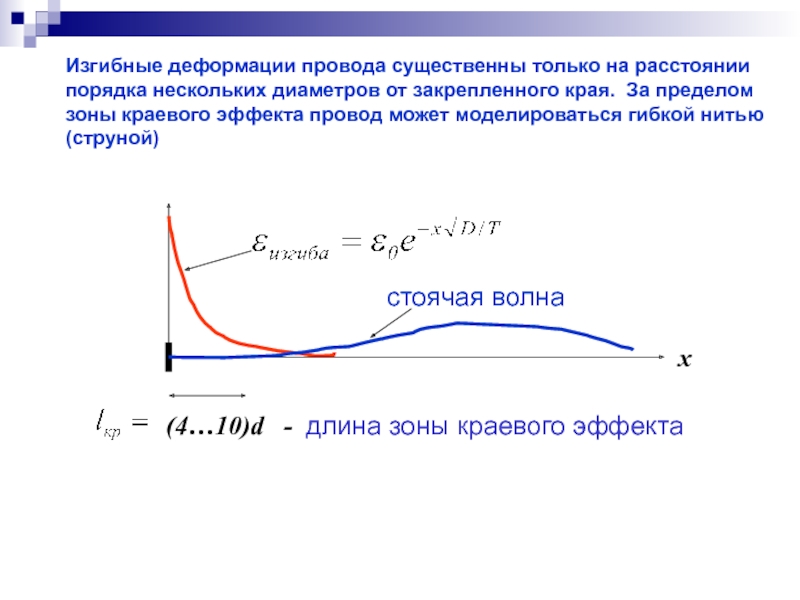
- 8. Изгибные деформации провода существенны только на расстоянии
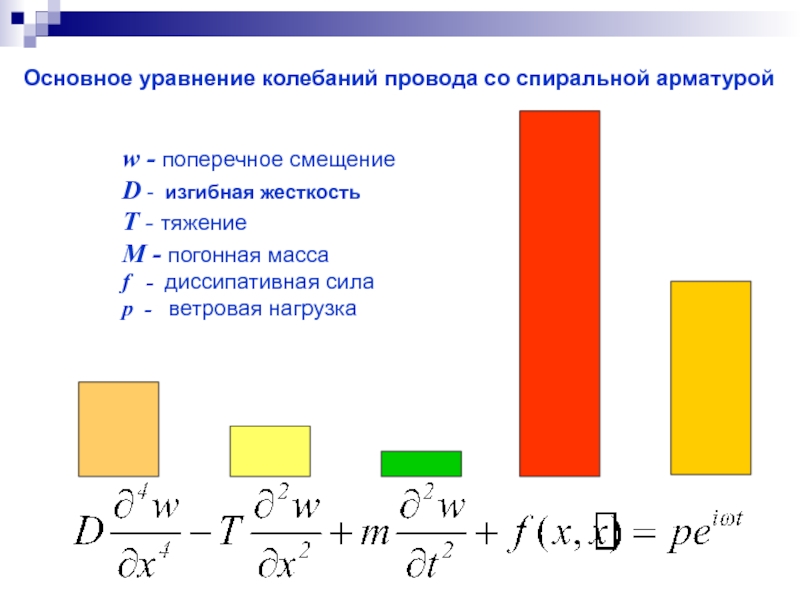
- 9. Основное уравнение колебаний провода со спиральной арматурой
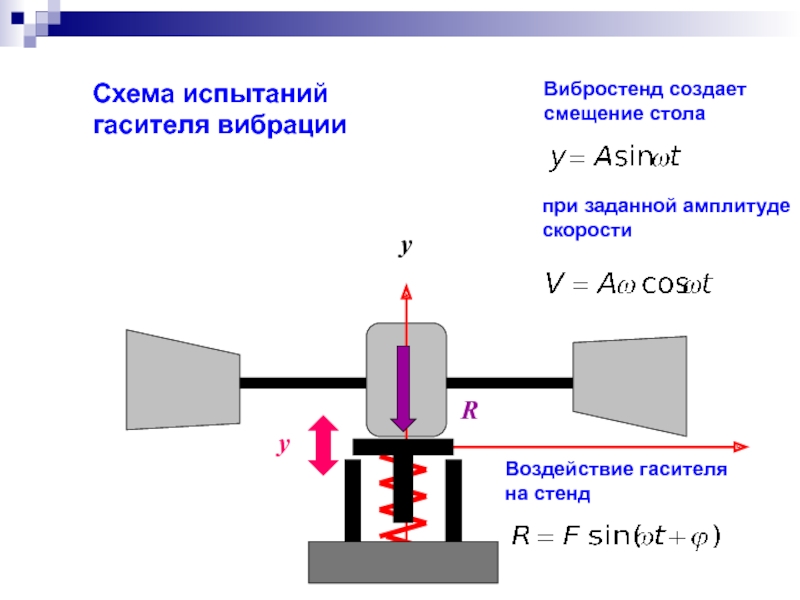
- 10. Гаситель вибрации типа Стокбриджа
- 11. Модель гасителя колебаний Основные
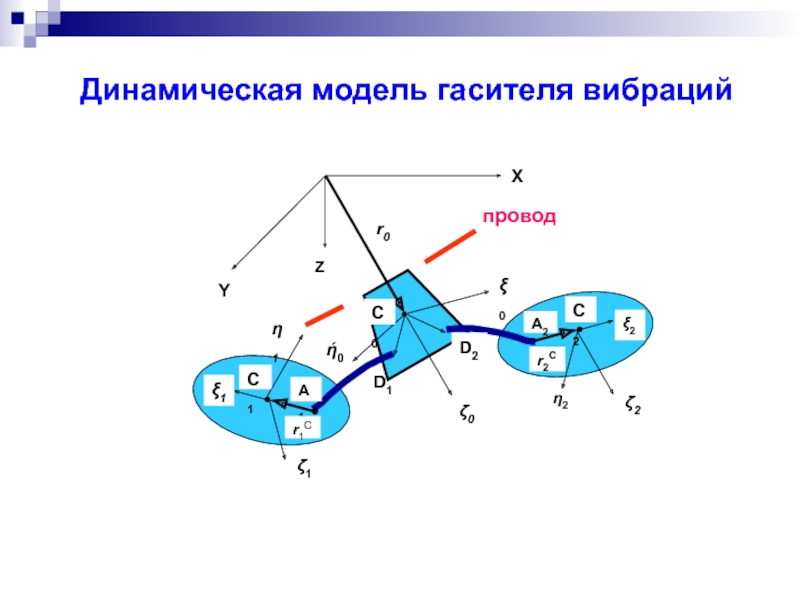
- 12. Динамическая модель гасителя вибраций
- 13. Уравнения колебаний гасителя Кинетическая и потенциальная энергии
- 14. Система сил и моментов, действующих на гаситель
- 16. Сравнение результатов расчетов и испытаний
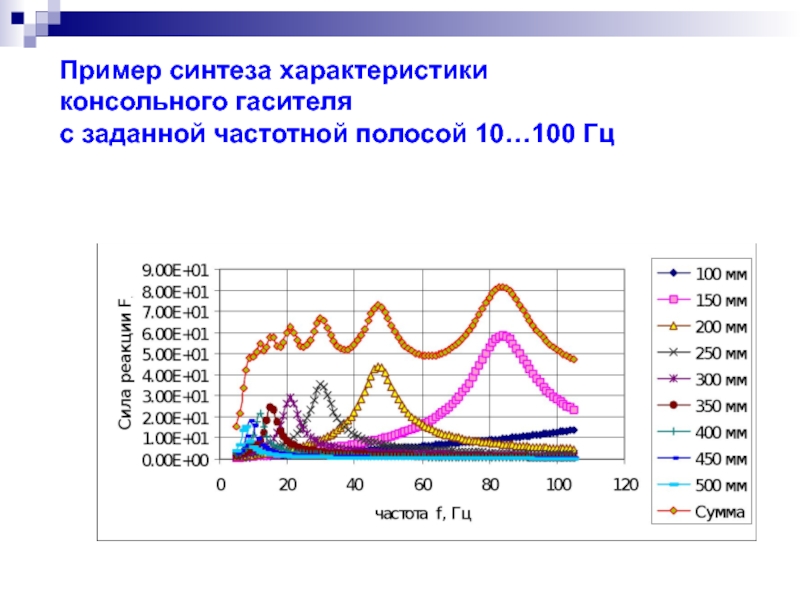
- 18. Пример синтеза характеристики консольного гасителя с заданной частотной полосой 10…100 Гц
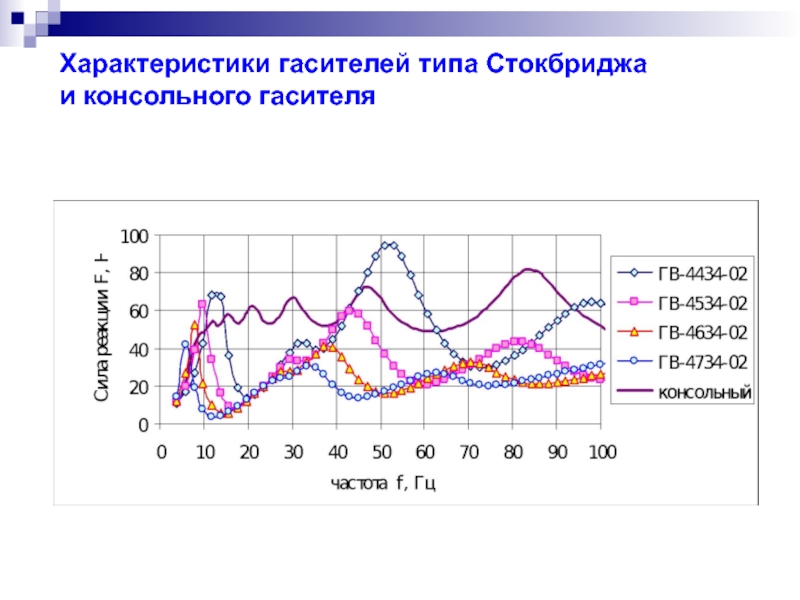
- 19. Характеристики гасителей типа Стокбриджа и консольного гасителя
- 20. Арматура натяжных зажимов
- 21. Модель гирлянды изоляторов z yn-1 B
- 22. Метод решения уравнений: метод начальных параметров в
- 24. Динамические свойства четырехполюсников задаются их переходными
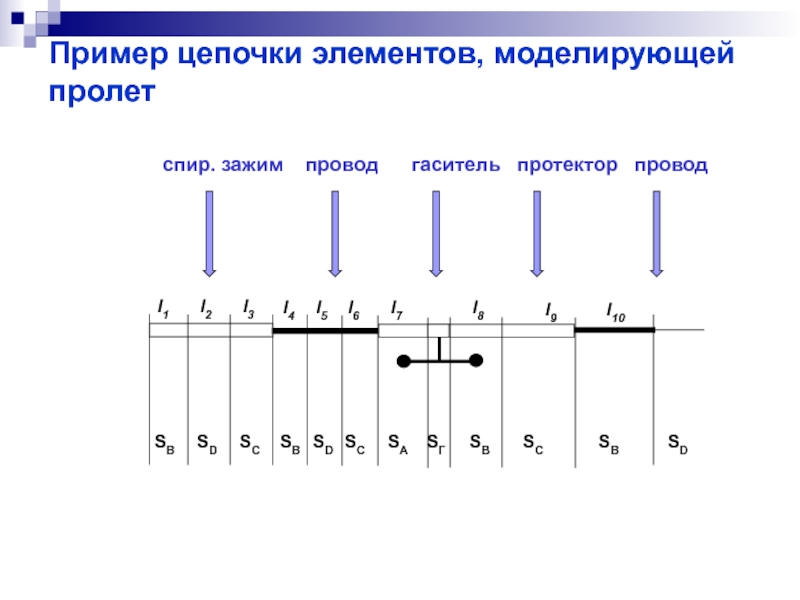
- 26. Пример цепочки элементов, моделирующей пролет
- 27. Расщепленная фаза
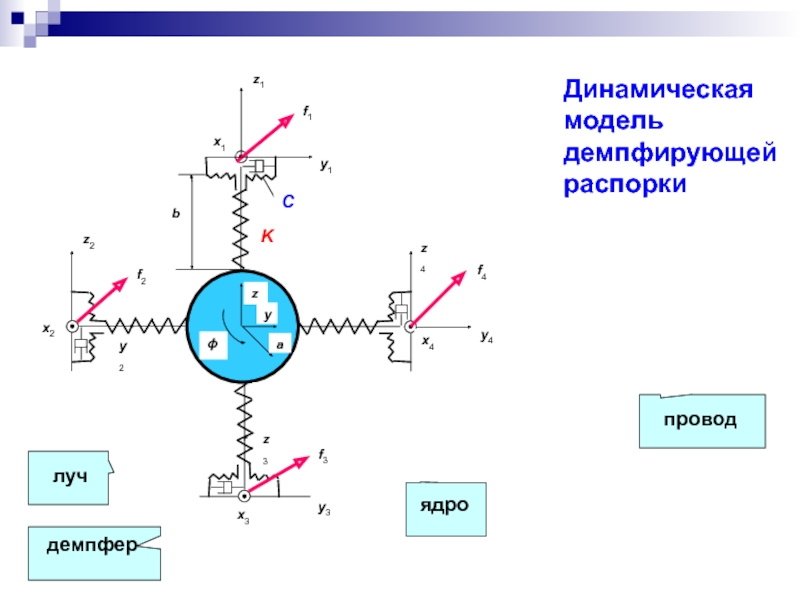
- 29. Динамическая модель демпфирующей распорки
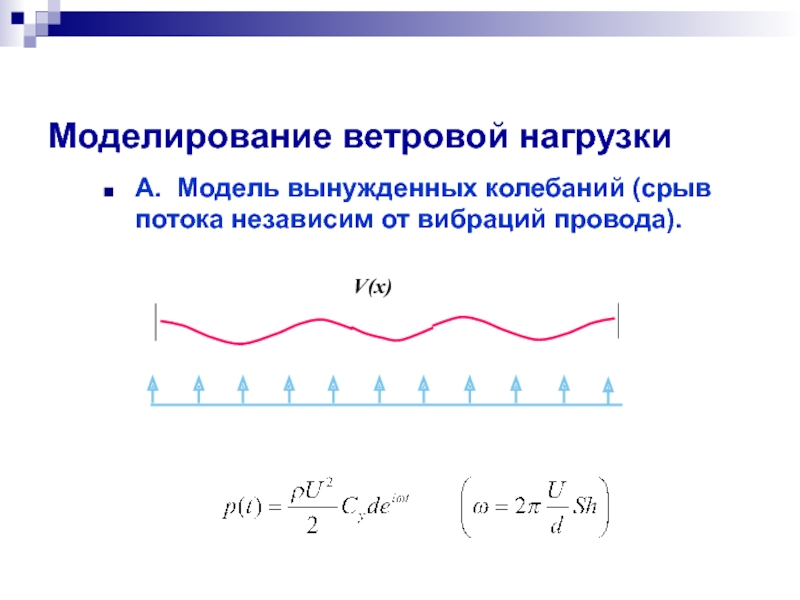
- 30. Моделирование ветровой нагрузки А. Модель вынужденных колебаний (срыв потока независим от вибраций провода).
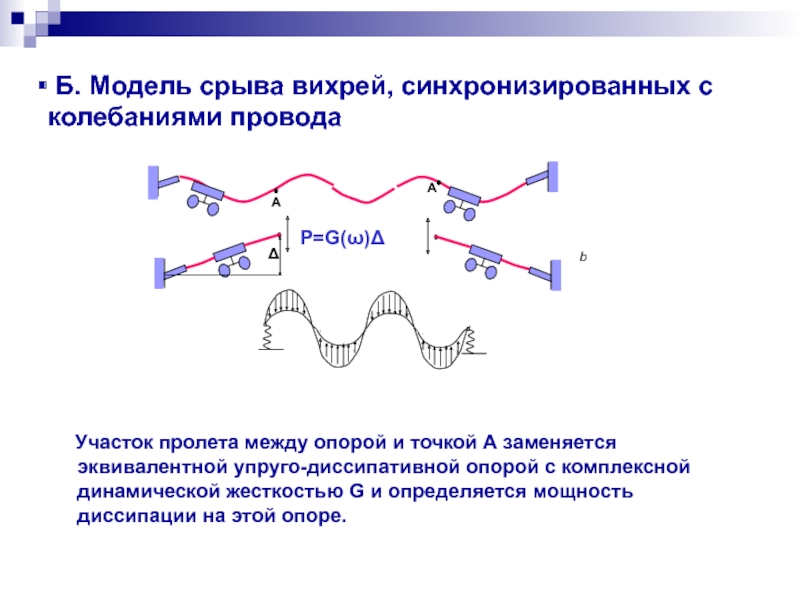
- 31. Б. Модель срыва вихрей, синхронизированных с
- 32. Моделирование диссипативных сил имеет определяющее
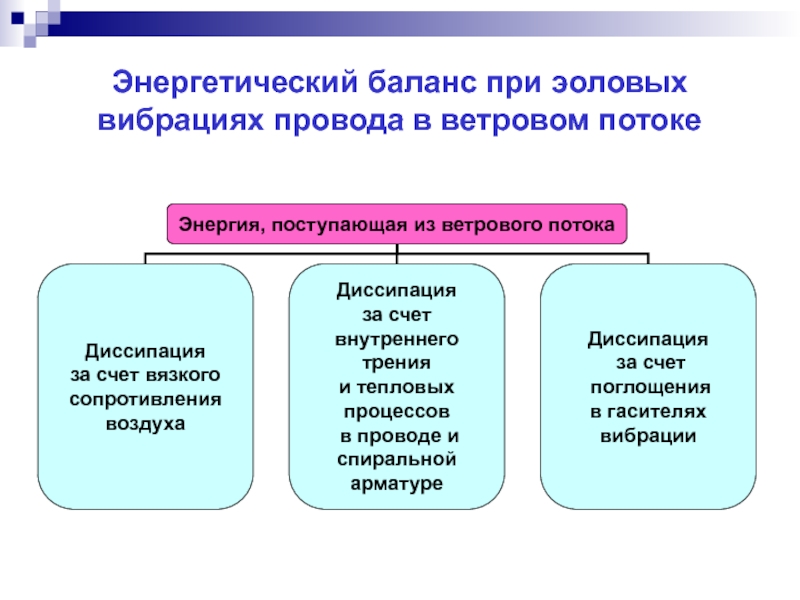
- 33. Энергетический баланс при эоловых вибрациях провода в ветровом потоке
- 34. Энергетический баланс
- 36. Компоненты энергетического баланса А. Скорость притока энергии,
- 37. Б. Мощность диссипации за счет сопротивления воздуха
- 38. Скорость убывания кинетической энергии вследствие перехода в
- 39. Г. Мощность самодемпфирования провода
- 40. Д. Диссипация в гасителях вибрации и спиральной
- 41. Уравнение для определения амплитуды колебаний провода в пролете на основе энергетического баланса
- 42. А. Метод, основанный на регистрации затухания амплитуды
- 43. Связь коэффициента внутреннего трения с декрементом колебаний
- 44. Затухание амплитуды при удалении от источника возбуждения
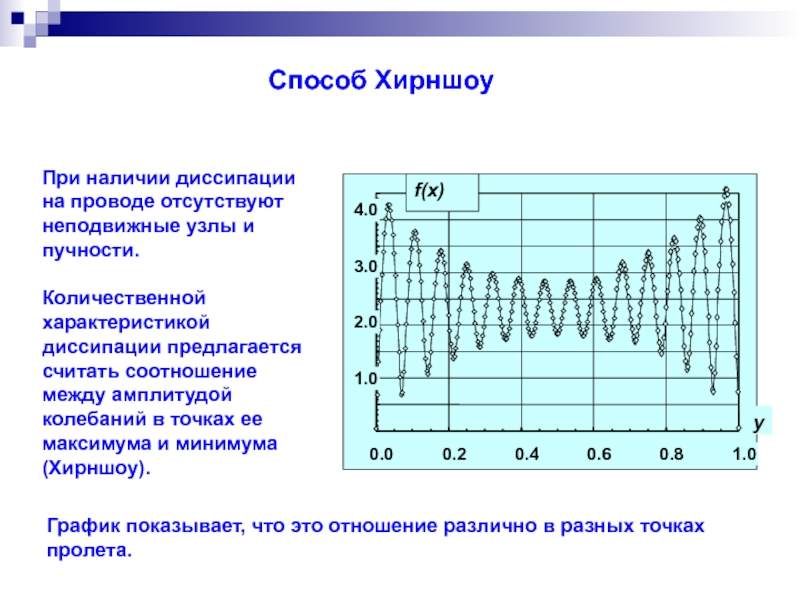
- 45. Способ Хирншоу
- 46. Характеристика диссипации провода по Хирншоу и ее
- 47. Энергетически эквивалентная модель колебаний при амплитудно-зависимом демпфировании Исходная модель: Эквивалентная модель:
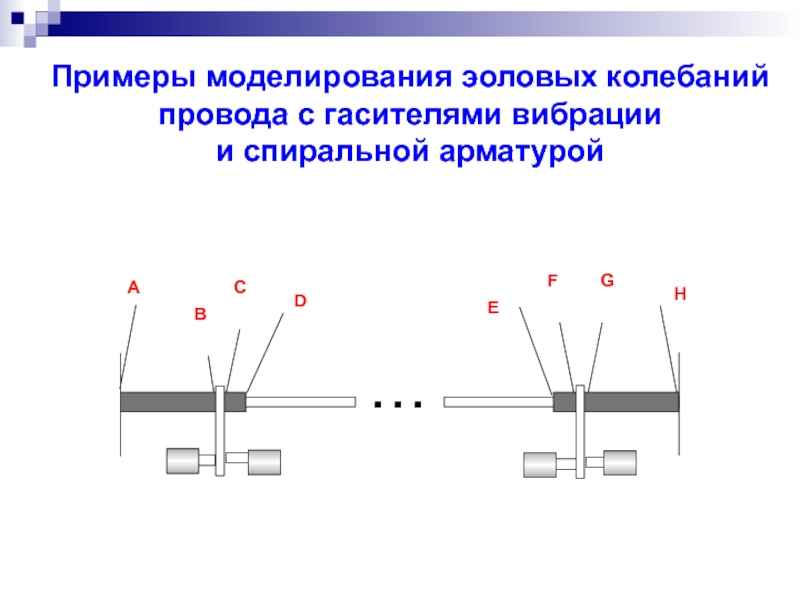
- 48. Примеры моделирования эоловых колебаний провода с гасителями вибрации и спиральной арматурой
- 49. Спиральная арматура и гасители колебаний существенно
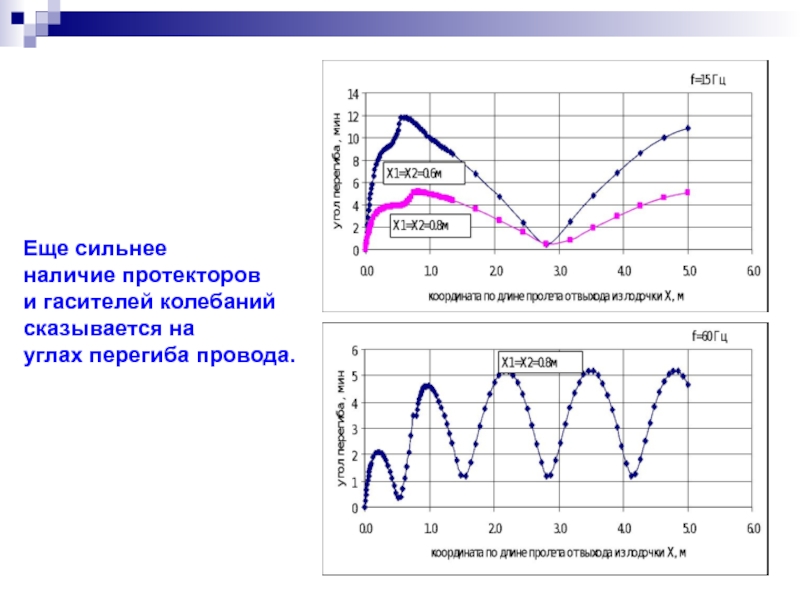
- 50. Еще сильнее наличие протекторов и
- 51. Наиболее чувствительны к установке гасителей
- 52. Зависимость изгибной деформации провода
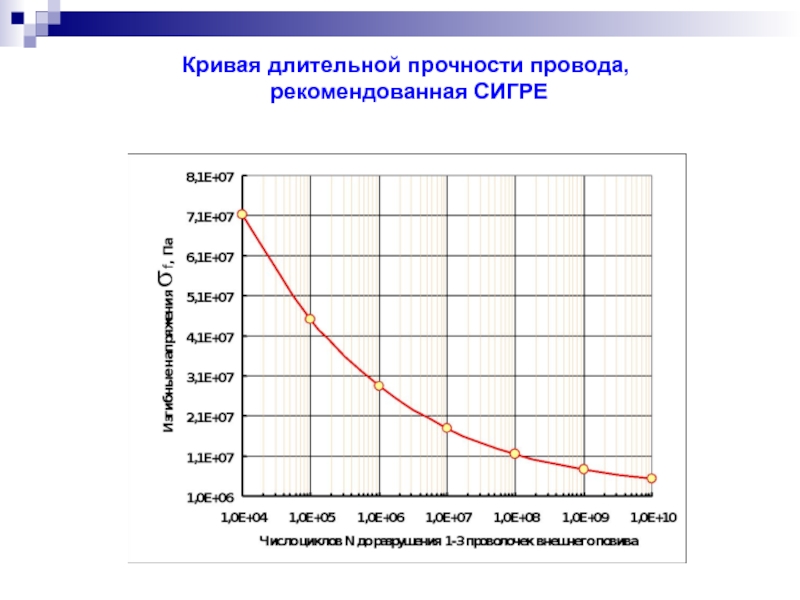
- 53. Кривая длительной прочности провода, рекомендованная СИГРЕ
- 54. Минимизация изгибных деформаций провода путем
- 56. Число циклов до разрушения при улучшенной
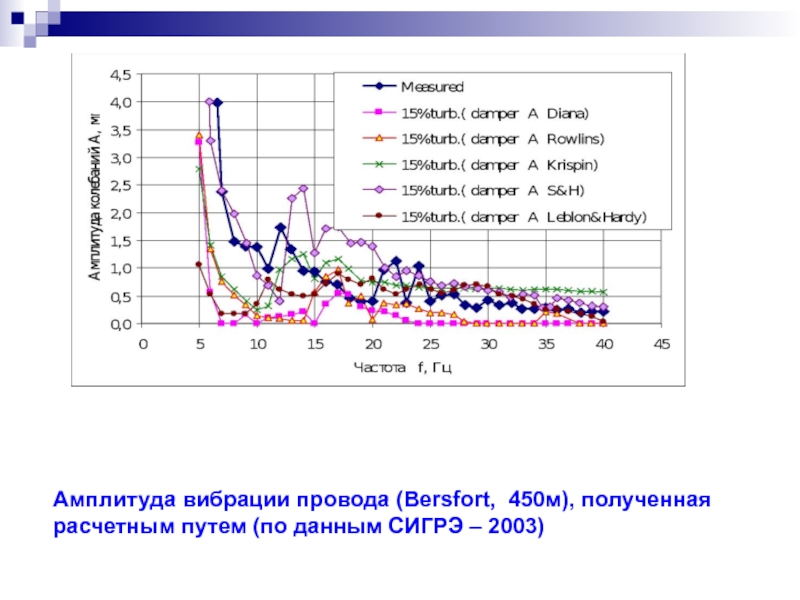
- 57. Амплитуда вибрации провода (Bersfort, 450м), полученная расчетным путем (по данным СИГРЭ – 2003)
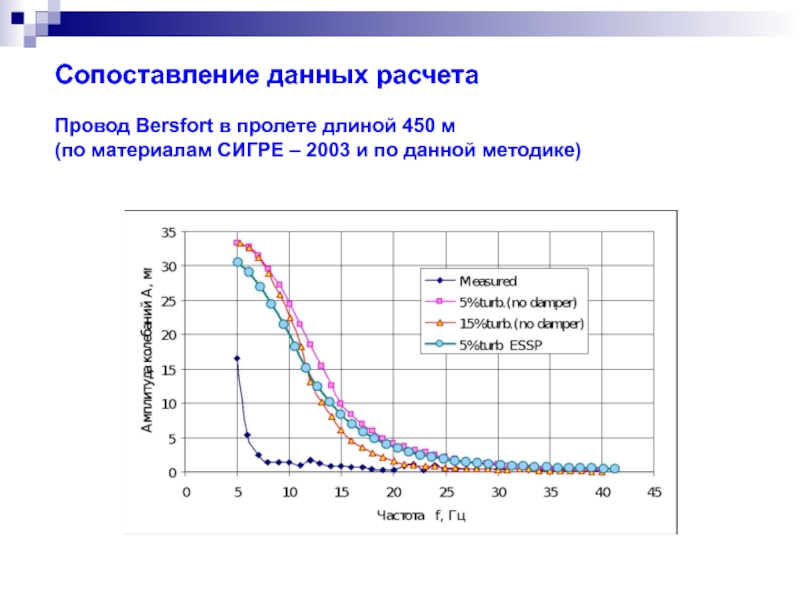
- 58. Сопоставление данных расчета Провод
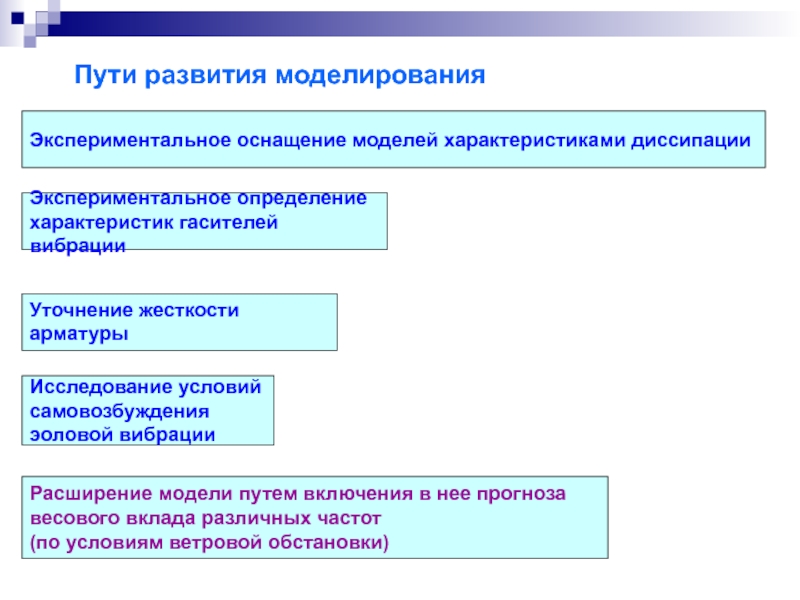
- 59. Пути развития моделирования
Объект моделирования пролет ЛЭП провод, спиральная арматура, гасители вибрации, гирлянды изоляторов
Слайд 1Методы
математического моделирования
для проектирования
защиты пролетов ЛЭП
от эоловых вибраций
Слайд 2Объект моделирования
пролет ЛЭП
провод,
спиральная арматура,
гасители
вибрации,
гирлянды изоляторов
гирлянды изоляторов
Слайд 5Факторы, учитываемые при моделировании: длина пролета, тяжение провода, тип провода (погонная масса, диаметр,
изгибная жесткость, характеристики демпфирования),
спиральная арматура (погонная масса, изгибная жесткость,
характеристики демпфирования),
гасители вибрации (конструктивная схема, массы конструктивных элементов, тензор инерции грузов, длина и изгибная жесткость тросиков, характеристики демпфирования),
натяжные или поддерживающие зажимы, гирлянды изоляторов,
скорость ветра, аэродинамические характеристики провода.
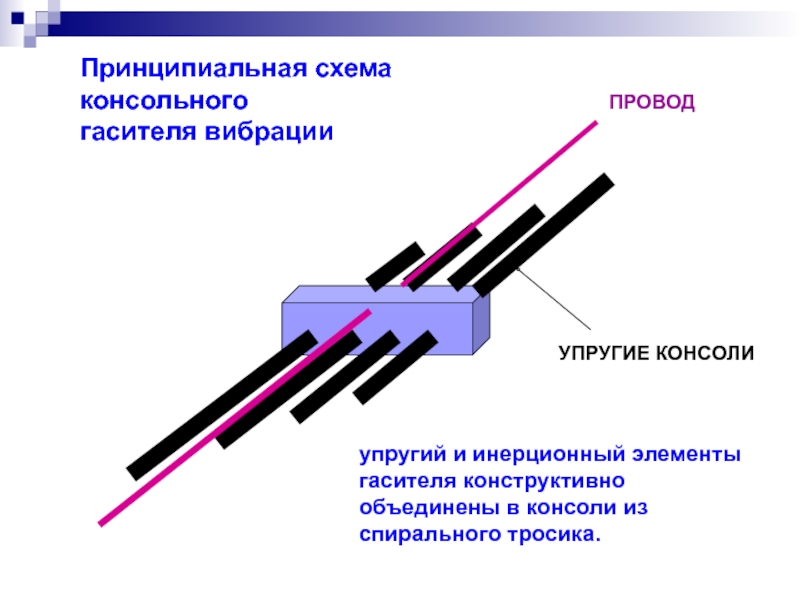
Слайд 6Провод и спиральная арматура:
Модель A - упругая балка. Используется для коротких
участков провода, спиральных протекторов и зажимов.
Модель D - гибкая нить (струна). Используется для длинных участков провода, расположенных вдали от границ пролета.
Модели B и С - упругая «односторонняя балка» - переходные модели, связывающие балочные к струнные участки.
Другие конструктивные элементы:
Модель E - гасители вибрации.
Модель G - гирлянды изоляторов.
Модель D - гибкая нить (струна). Используется для длинных участков провода, расположенных вдали от границ пролета.
Модели B и С - упругая «односторонняя балка» - переходные модели, связывающие балочные к струнные участки.
Другие конструктивные элементы:
Модель E - гасители вибрации.
Модель G - гирлянды изоляторов.
Модели конструктивных элементов пролета
Слайд 8Изгибные деформации провода существенны только на расстоянии порядка нескольких диаметров от
закрепленного края. За пределом зоны краевого эффекта провод может моделироваться гибкой нитью (струной)
Слайд 11Модель гасителя колебаний
Основные предположения , положенные в основу
модели гасителя вибрации:
модель относится к гасителям типа Стокбриджа, у которых упругие элементы выполнены в виде упругих тросиков, а инерционные – в виде массивных грузов
тросики моделируются безынерционными консольными линейно-упругими балками с внутренним трением, изгибающимися в двух ортогональных плоскостях
упругие характеристики тросиков заданы матрицей, связывающей кинематический вектор (прогибы и углы поворота) с динамическим вектором (изгибающие моменты и поперечные силы)
диссипация в тросиках учитывается на основе теории внутреннего трения (жесткости тросиков – комплексные)
грузы и узел крепления гасителя к проводу моделируются твердыми телами с 6 степенями свободы; инерционные характеристики заданы их тензорами инерции
модель относится к гасителям типа Стокбриджа, у которых упругие элементы выполнены в виде упругих тросиков, а инерционные – в виде массивных грузов
тросики моделируются безынерционными консольными линейно-упругими балками с внутренним трением, изгибающимися в двух ортогональных плоскостях
упругие характеристики тросиков заданы матрицей, связывающей кинематический вектор (прогибы и углы поворота) с динамическим вектором (изгибающие моменты и поперечные силы)
диссипация в тросиках учитывается на основе теории внутреннего трения (жесткости тросиков – комплексные)
грузы и узел крепления гасителя к проводу моделируются твердыми телами с 6 степенями свободы; инерционные характеристики заданы их тензорами инерции
Слайд 13Уравнения колебаний гасителя
Кинетическая и потенциальная энергии гасителя вибрации как системы с
18 степенями свободы:
Уравнения колебаний системы
(С- ω2А) q = р
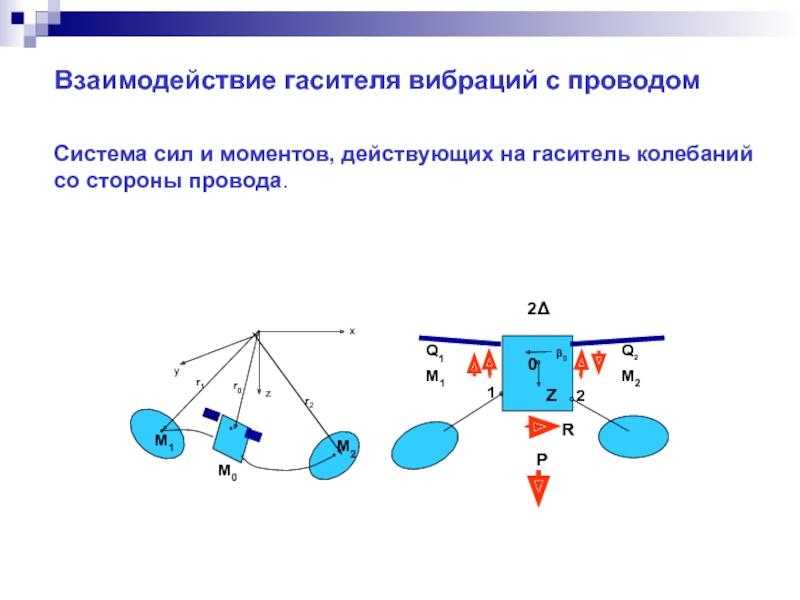
Слайд 14Система сил и моментов, действующих на гаситель колебаний со стороны провода.
2Δ
M1
M0
М2
x
y
z
r1
r0
r2
0
Z
β0
M1
M2
Q1
Q2
R
P
1
2
Взаимодействие гасителя вибраций с проводом
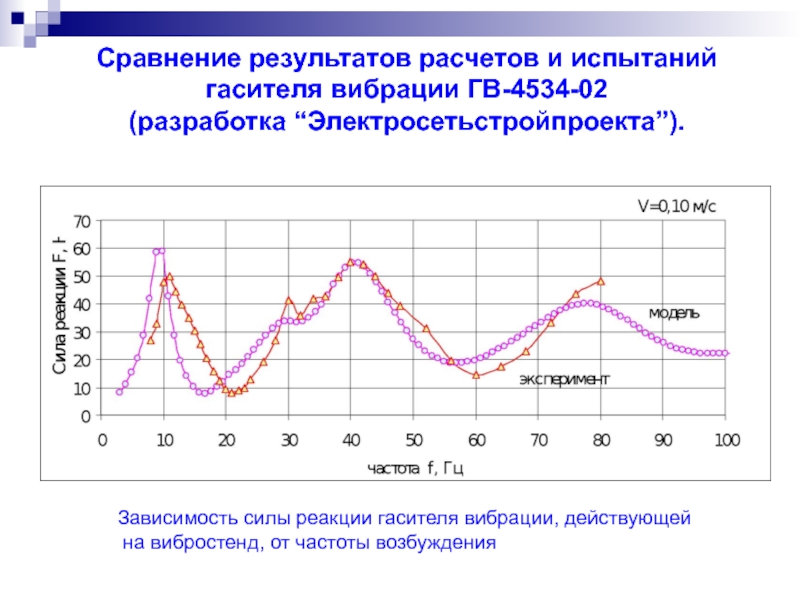
Слайд 16
Сравнение результатов расчетов и испытаний
гасителя вибрации ГВ-4534-02
(разработка “Электросетьстройпроекта”).
Зависимость силы
реакции гасителя вибрации, действующей
на вибростенд, от частоты возбуждения
на вибростенд, от частоты возбуждения
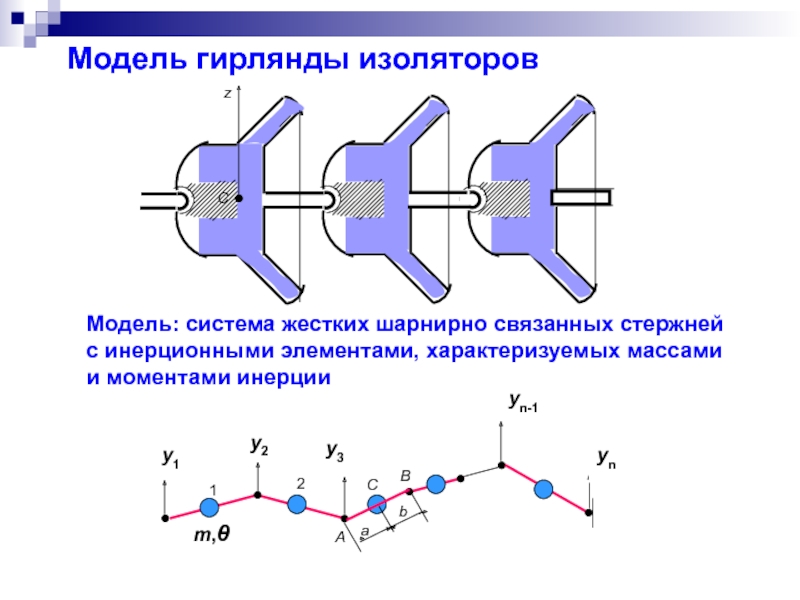
Слайд 21Модель гирлянды изоляторов
z
yn-1
B
C
b
a
y3
A
m,θ
y2
2
1
yn
y1
Модель: система жестких шарнирно связанных стержней
с инерционными элементами,
характеризуемых массами
и моментами инерции
и моментами инерции
Слайд 22Метод решения уравнений:
метод начальных параметров в матричной форме
Аргументы в пользу выбора
метода:
решение задачи остается в классе “точных”
размерность задачи не зависит от числа конструктивных элементов пролета (протекторов, гасителей, промежуточных участков провода)
алгоритм расчета не усложняется при включении дополнительного элемента
решение задачи остается в классе “точных”
размерность задачи не зависит от числа конструктивных элементов пролета (протекторов, гасителей, промежуточных участков провода)
алгоритм расчета не усложняется при включении дополнительного элемента
Слайд 23
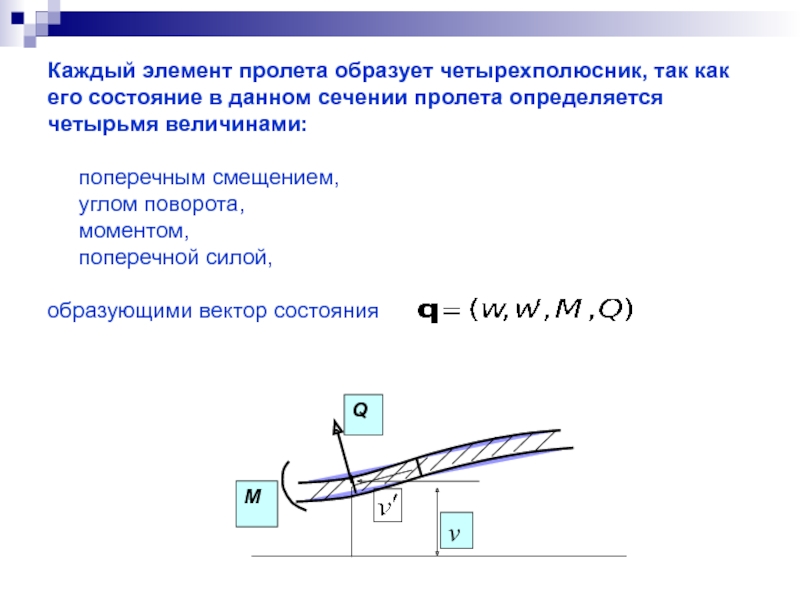
Каждый элемент пролета образует четырехполюсник, так
как его состояние в данном сечении пролета определяется четырьмя величинами:
поперечным смещением,
углом поворота,
моментом,
поперечной силой,
образующими вектор состояния
поперечным смещением,
углом поворота,
моментом,
поперечной силой,
образующими вектор состояния
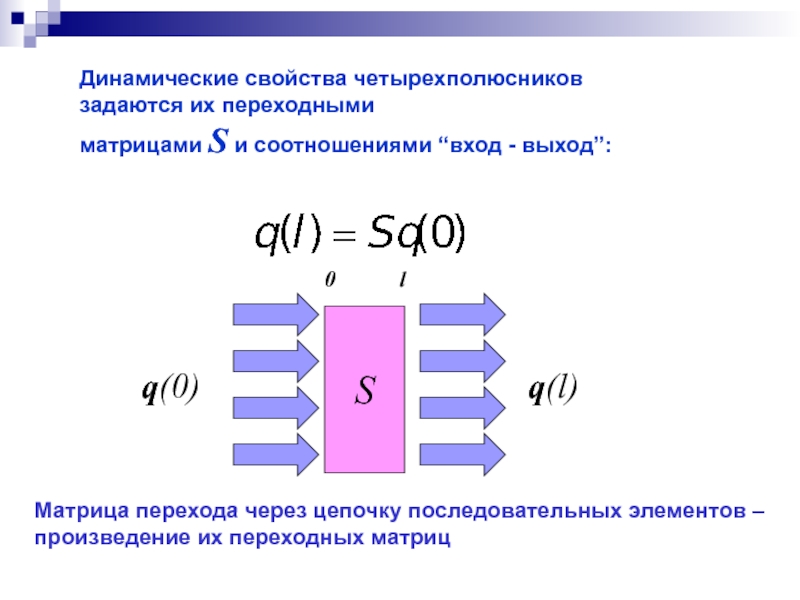
Слайд 24Динамические свойства четырехполюсников
задаются их переходными
матрицами S и соотношениями “вход
- выход”:
Матрица перехода через цепочку последовательных элементов –
произведение их переходных матриц
Слайд 25
…
=
=
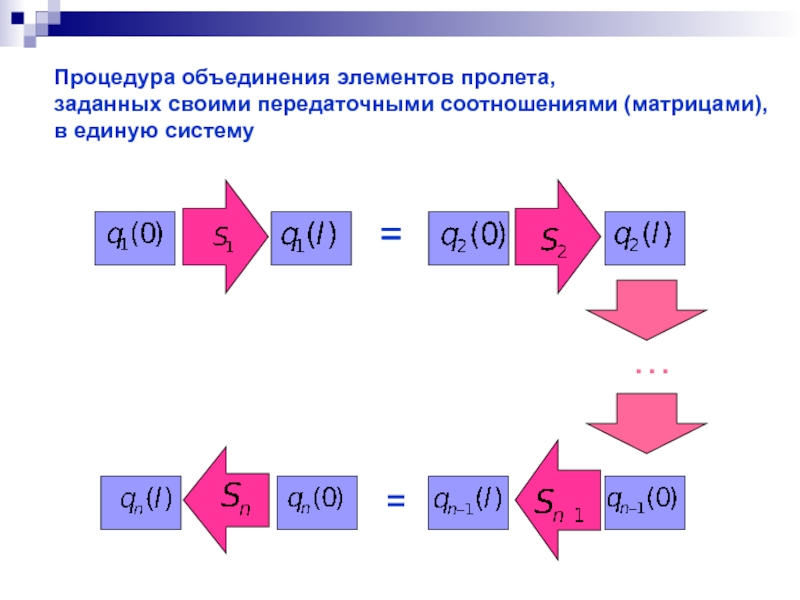
Процедура объединения элементов пролета,
заданных своими передаточными соотношениями (матрицами),
в единую систему
Слайд 28
A
C
B
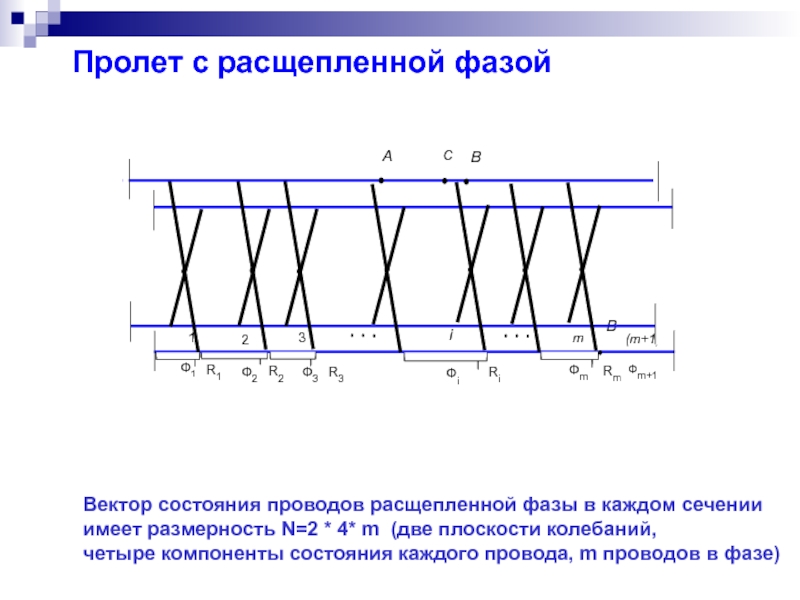
Пролет с расщепленной фазой
Вектор состояния проводов расщепленной фазы в каждом сечении
имеет
размерность N=2 * 4* m (две плоскости колебаний,
четыре компоненты состояния каждого провода, m проводов в фазе)
четыре компоненты состояния каждого провода, m проводов в фазе)
Слайд 30Моделирование ветровой нагрузки
А. Модель вынужденных колебаний (срыв потока независим от вибраций
провода).
Слайд 31 Б. Модель срыва вихрей, синхронизированных с колебаниями провода
Участок пролета между опорой и точкой А заменяется эквивалентной упруго-диссипативной опорой с комплексной динамической жесткостью G и определяется мощность диссипации на этой опоре.
Слайд 32Моделирование
диссипативных сил
имеет определяющее значение для
моделирования эоловых вибраций
проводов.
Определение диссипативных характеристик
–
задача экспериментальная, но она
“должна быть передана экспериментаторам
как можно позже” (К. Трусделл).
задача экспериментальная, но она
“должна быть передана экспериментаторам
как можно позже” (К. Трусделл).
Слайд 36Компоненты энергетического баланса
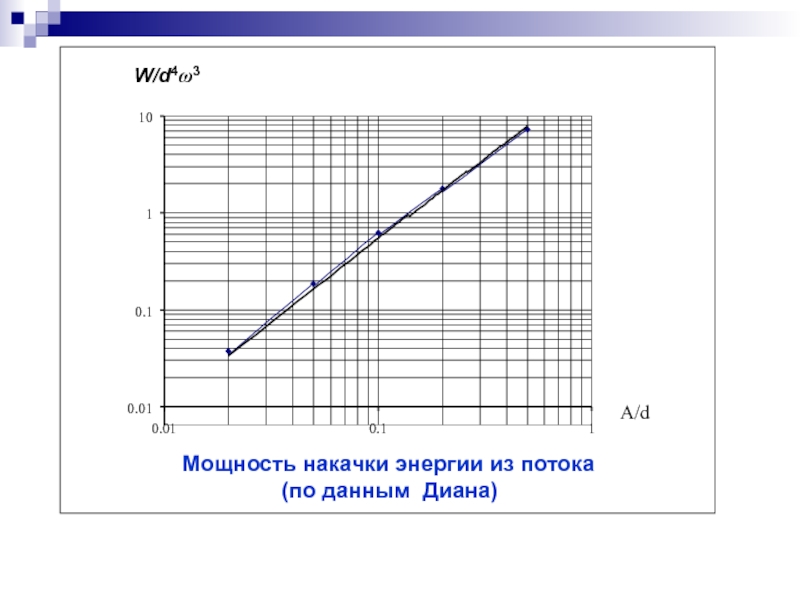
А. Скорость притока энергии,
поглощаемой проводом из ветрового потока
на одну полуволну (по Диана)
Слайд 37Б. Мощность диссипации за счет сопротивления воздуха
справедлив при низкочастотных колебаниях, характеризуемых
малыми значениями числа Рейнольдса
Закон сопротивления Стокса
Применительно к вибрации провода уже при d > 10 мм ,
ω > 10 рад/с и ν = 0,15⋅10-4 , Re > 60
и закон сопротивления Стокса не имеет места.
Возникает режим обтекания, характерный тем,
что завихренность потока, обусловленная вязкостью воздуха,
существенна только вблизи поверхности провода
и экспоненциально убывает при удалении от него.
Коэффициент вязкого сопротивления зависит от частоты (Л.Д. Ландау):
Слайд 38Скорость убывания кинетической энергии вследствие перехода в тепло равна (Л.Д. Ландау):
В.
Термодинамический механизм диссипации
Слайд 39Г. Мощность самодемпфирования провода
Диссипативная составляющая изгибающего момента в
проводе равна
Мощность диссипации на одной полуволне:
Слайд 40Д. Диссипация в гасителях вибрации и спиральной арматуре
Участок
пролета между опорой и точкой А заменяется эквивалентной упруго-диссипативной опорой с комплексной динамической жесткостью G и определяется мощность диссипации участка пролета от опоры до точки А:
Слайд 41 Уравнение для определения амплитуды колебаний провода в пролете на основе энергетического
баланса
Слайд 42А. Метод, основанный на регистрации затухания амплитуды свободных колебаний во времени.
В. Метод, основанный на определении
затухания амплитуды вынужденных колебаний
по мере удаления от источника их возбуждения.
С. Метод, основанный на сравнении
амплитуд колебаний в точках их максимумов
и минимумов (Хирншоу).
Основные экспериментальные
методы определения характеристик диссипации
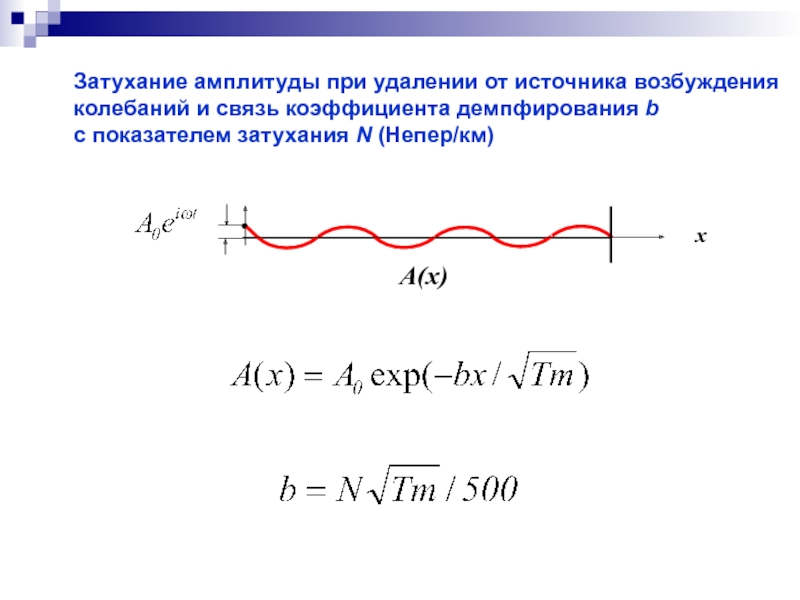
Слайд 44Затухание амплитуды при удалении от источника возбуждения колебаний и связь коэффициента
демпфирования b
с показателем затухания N (Непер/км)
x
A(x)
Слайд 46Характеристика диссипации провода по Хирншоу и ее связь с коэффициентом демпфирования
(линейное частотнозависимое демпфирование)
Закон изменения максимальных и минимальных амплитуд по пролету:
Параметр Хирншоу:
Коэффициент демпфирования,
выраженный через параметр Хирншоу в центре пролета
Слайд 47Энергетически эквивалентная модель колебаний при амплитудно-зависимом демпфировании
Исходная модель:
Эквивалентная модель:
Слайд 49
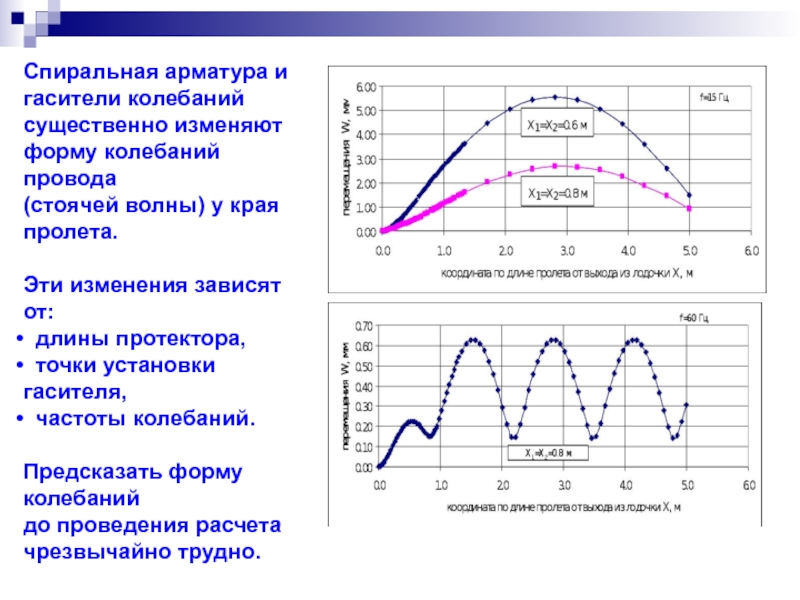
Спиральная арматура и
гасители колебаний
существенно изменяют
форму колебаний провода
(стоячей волны) у края
пролета.
Эти
изменения зависят от:
длины протектора,
точки установки гасителя,
частоты колебаний.
Предсказать форму колебаний
до проведения расчета
чрезвычайно трудно.
длины протектора,
точки установки гасителя,
частоты колебаний.
Предсказать форму колебаний
до проведения расчета
чрезвычайно трудно.
Слайд 51
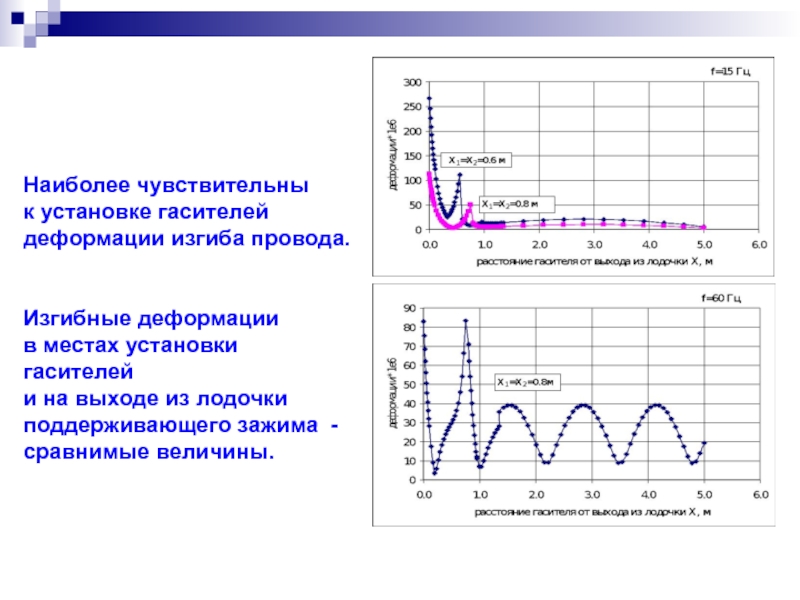
Наиболее чувствительны
к установке гасителей
деформации изгиба провода.
Изгибные деформации
в местах установки гасителей
и
на выходе из лодочки
поддерживающего зажима -
сравнимые величины.
поддерживающего зажима -
сравнимые величины.
Слайд 52
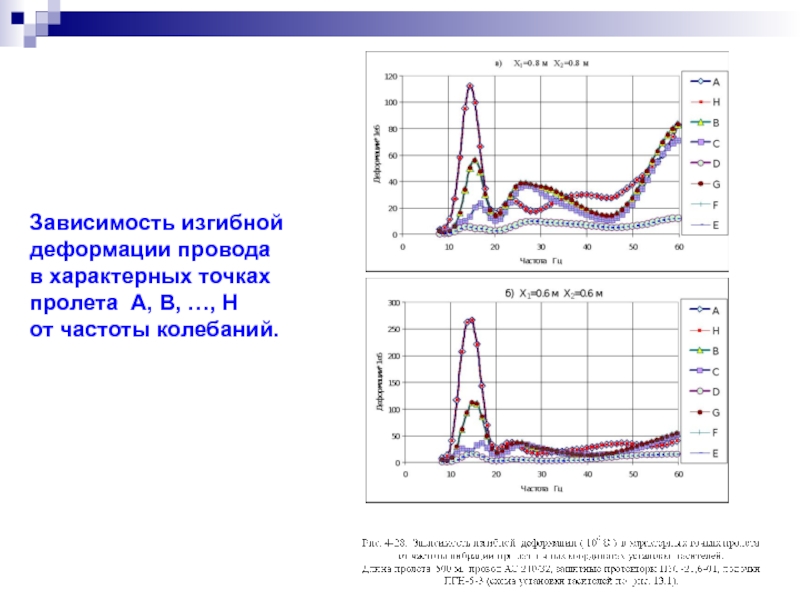
Зависимость изгибной
деформации провода
в характерных точках
пролета A, B, …, H
от
частоты колебаний.
Слайд 54
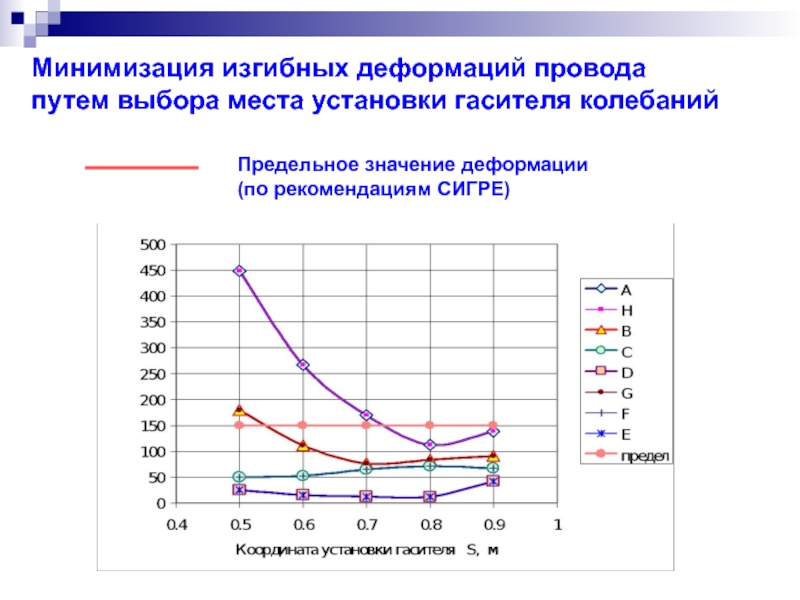
Минимизация изгибных деформаций провода
путем выбора места установки гасителя колебаний
Предельное значение
деформации
(по рекомендациям СИГРЕ)
(по рекомендациям СИГРЕ)
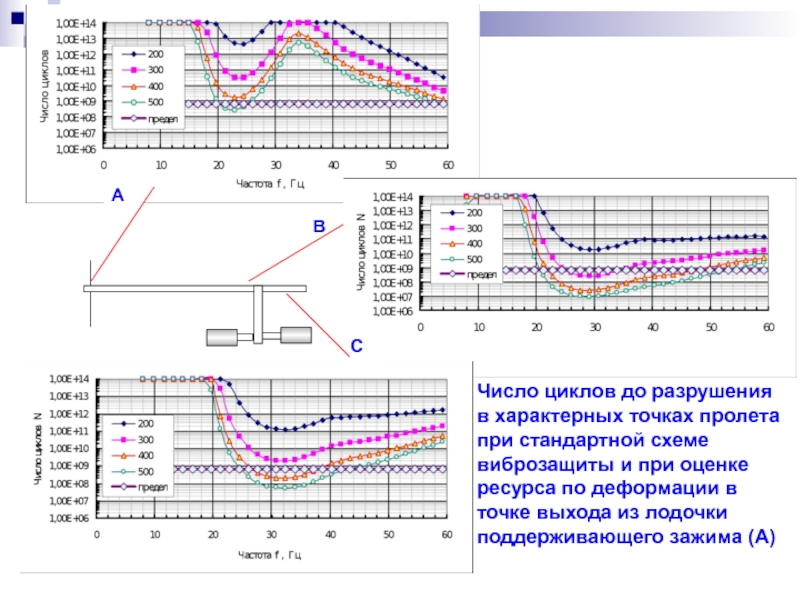
Слайд 55
Число циклов до разрушения
в характерных точках пролета
при стандартной схеме
виброзащиты и при оценке
ресурса по деформации в
точке выхода из лодочки
поддерживающего зажима (А)
А
C
B
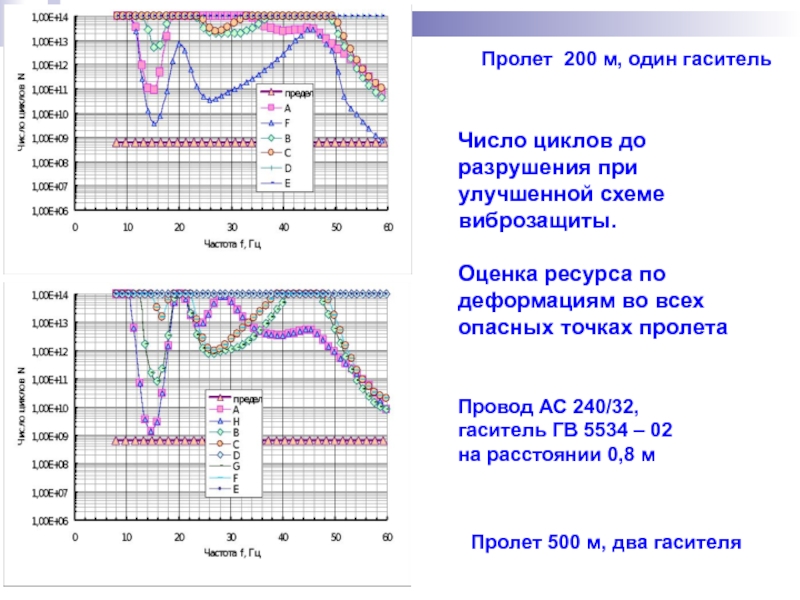
Слайд 56
Число циклов до разрушения при улучшенной схеме
виброзащиты.
Оценка ресурса по
деформациям
во всех опасных точках пролета
Провод АС 240/32,
гаситель ГВ 5534 – 02
на расстоянии 0,8 м
Провод АС 240/32,
гаситель ГВ 5534 – 02
на расстоянии 0,8 м
Пролет 200 м, один гаситель
Пролет 500 м, два гасителя
Слайд 57
Амплитуда вибрации провода (Bersfort, 450м), полученная
расчетным путем (по данным СИГРЭ –
2003)
Слайд 58
Сопоставление данных расчета
Провод Bersfort в пролете длиной 450 м
(по
материалам СИГРЕ – 2003 и по данной методике)
