ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального
образования
"ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра ГРНМ
Презентация
«ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»
Выполнил студент
группы 2Б780 Корнилов З.М.
Руководитель: доцент кафедры
высшей математики
Тарбокова Т.В.
Томск 2010
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования "ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ" презентация
Содержание
- 2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 1.1 Распределения случайные величины
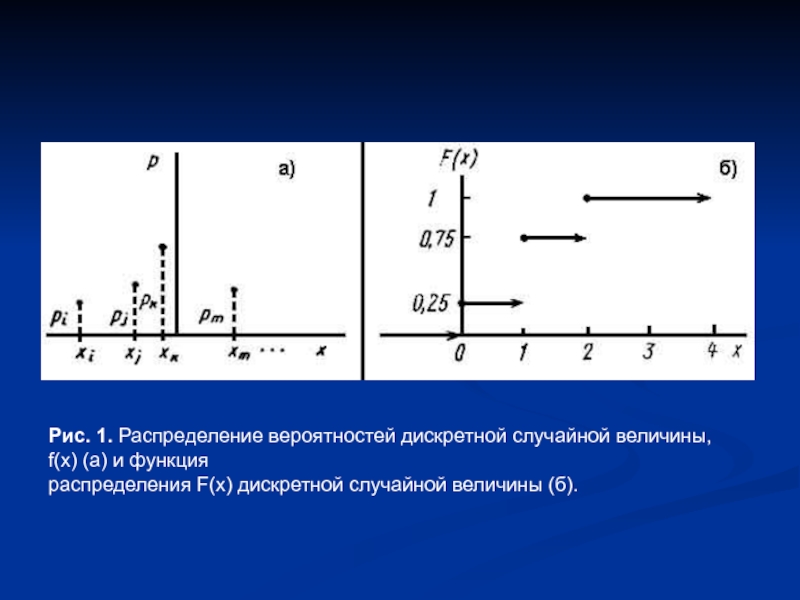
- 3. Рис. 1. Распределение вероятностей дискретной случайной величины,
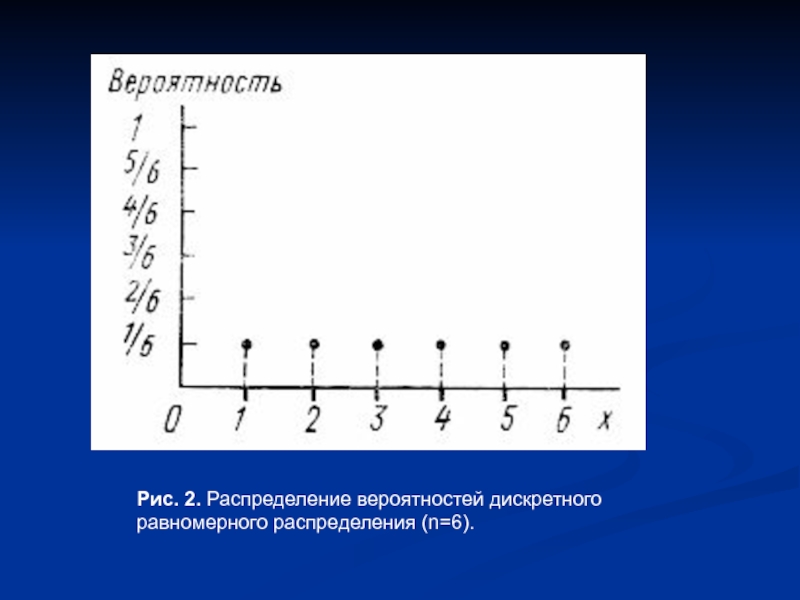
- 4. Рис. 2. Распределение вероятностей дискретного равномерного распределения (n=6).
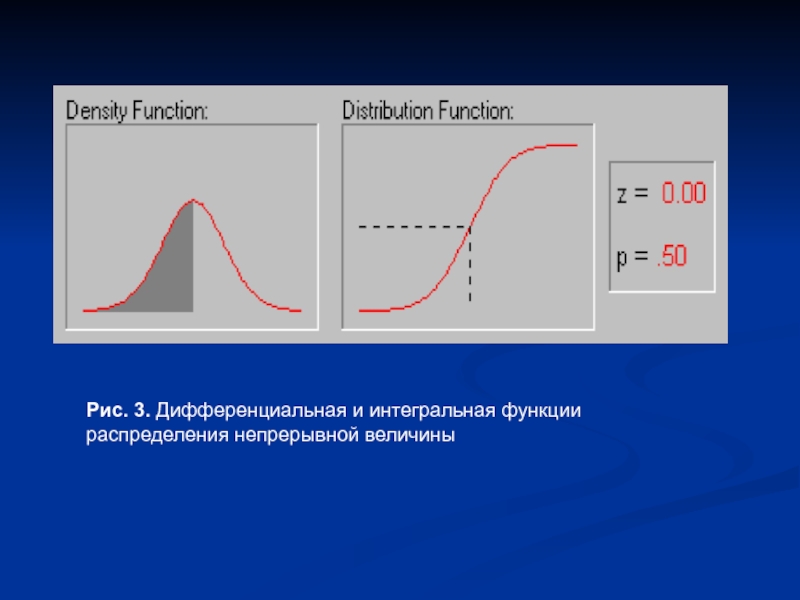
- 5. Рис. 3. Дифференциальная и интегральная функции распределения непрерывной величины
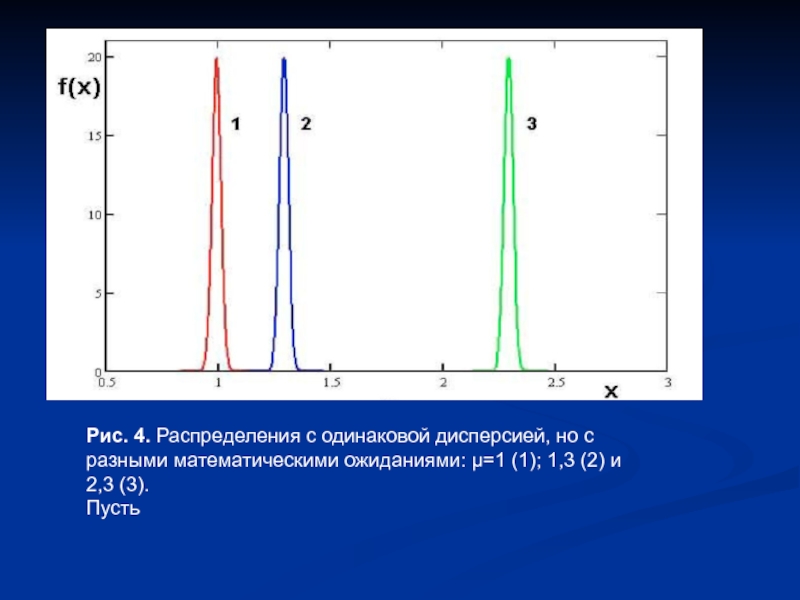
- 6. Рис. 4. Распределения с одинаковой дисперсией, но
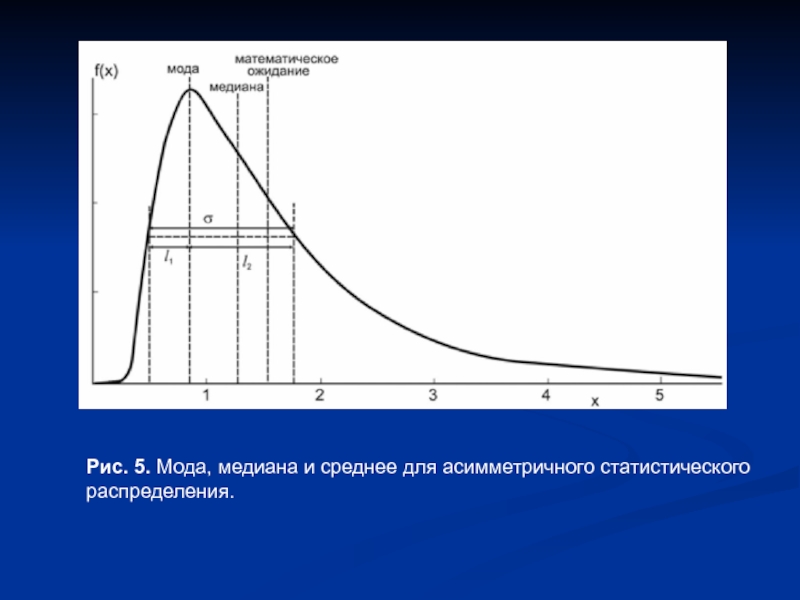
- 7. Рис. 5. Мода, медиана и среднее для асимметричного статистического распределения.
- 8. Рис. 6. а) Первая и третья квартили распределения. б) Графическая иллюстрация определения квантили.
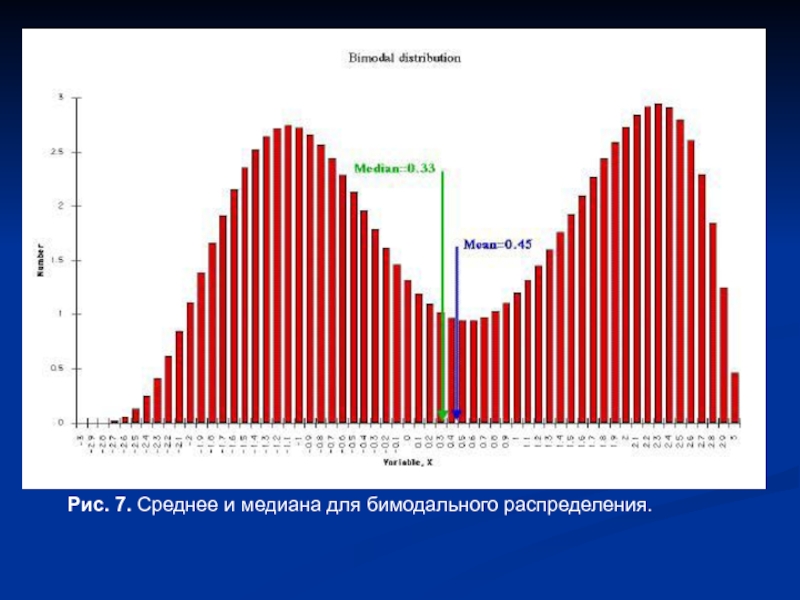
- 9. Рис. 7. Среднее и медиана для бимодального распределения.
- 10. Рис. 8. Распределения случайных величин с одинаковым средним значением, но различной дисперсией.
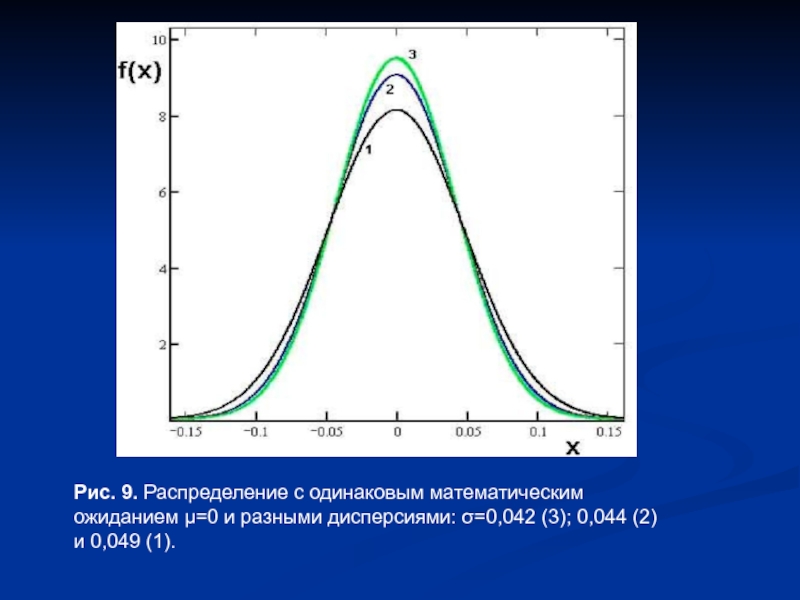
- 11. Рис. 9. Распределение с одинаковым математическим ожиданием
- 12. Рис. 10. Асимметрия (skewness).
- 13. Рис. 11. Эксцесс (kurtosis)
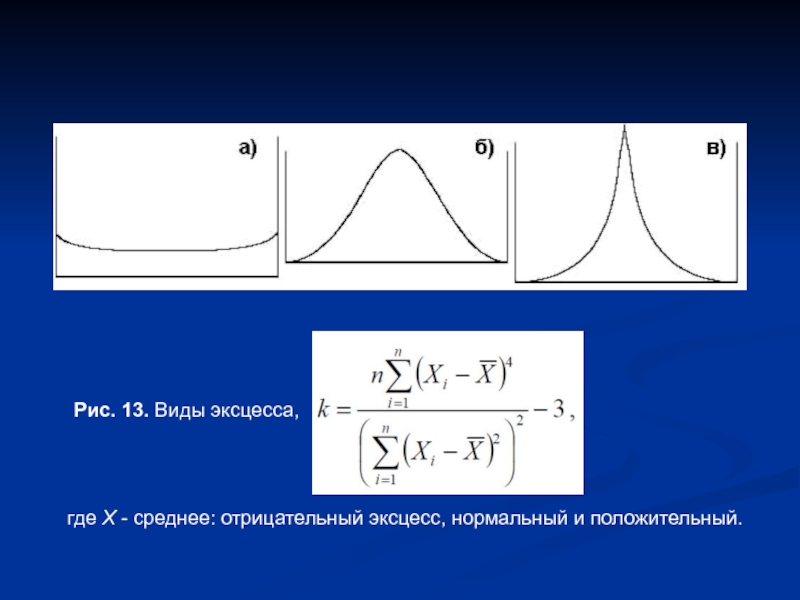
- 14. Рис. 13. Виды эксцесса, где X - среднее: отрицательный эксцесс, нормальный и положительный.
- 15. Рис. 15. Примеры Leptokurtic распределения: Лапласа, Логистическое,
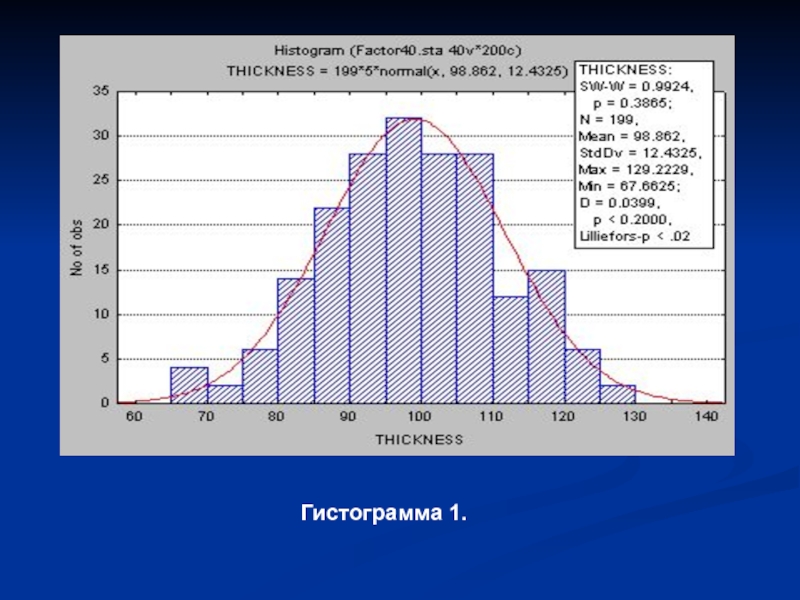
- 16. Гистограмма 1.
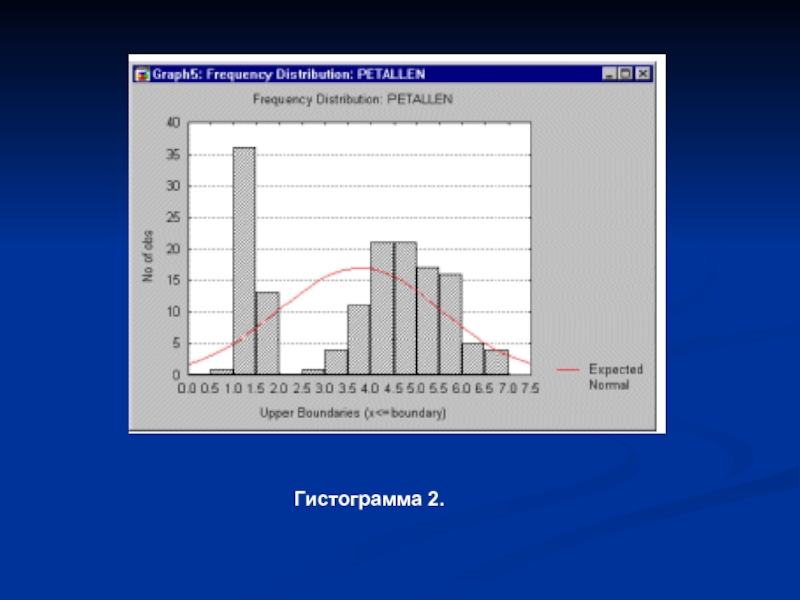
- 17. Гистограмма 2.
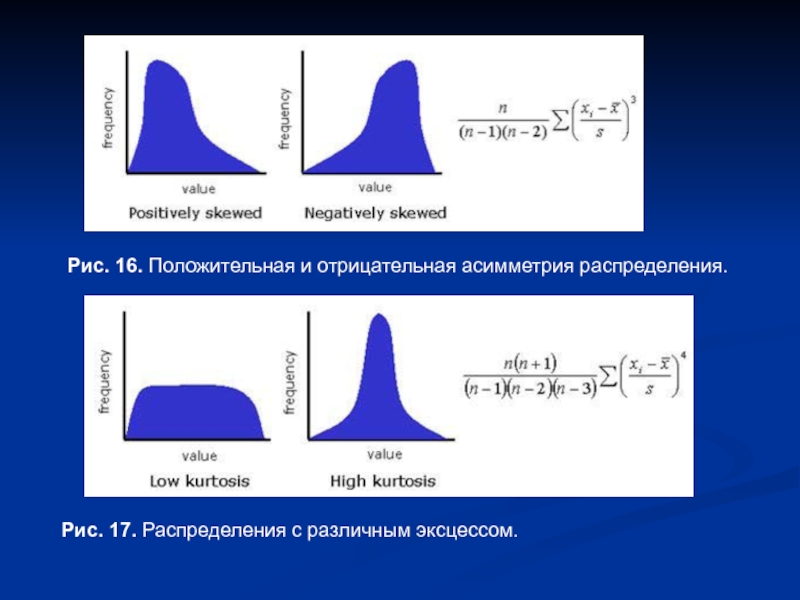
- 18. Рис. 16. Положительная и отрицательная асимметрия распределения. Рис. 17. Распределения с различным эксцессом.
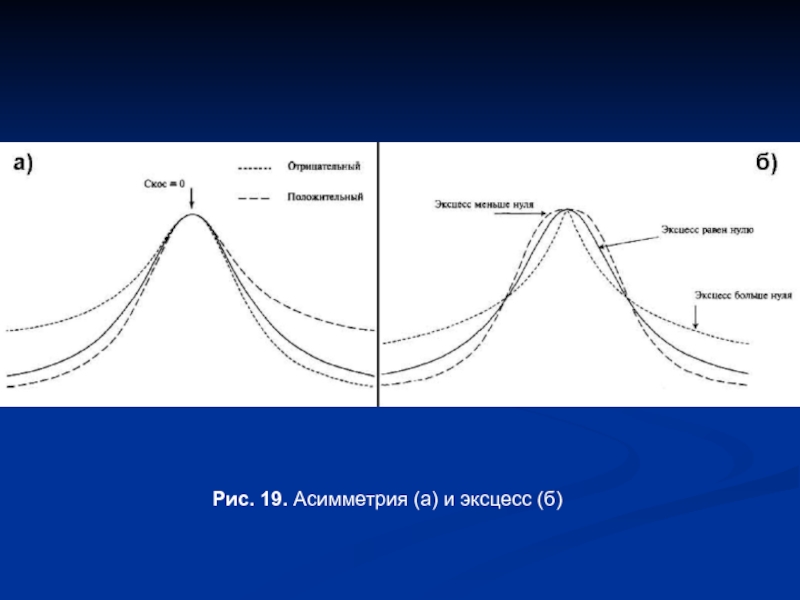
- 19. Рис. 19. Асимметрия (а) и эксцесс (б)
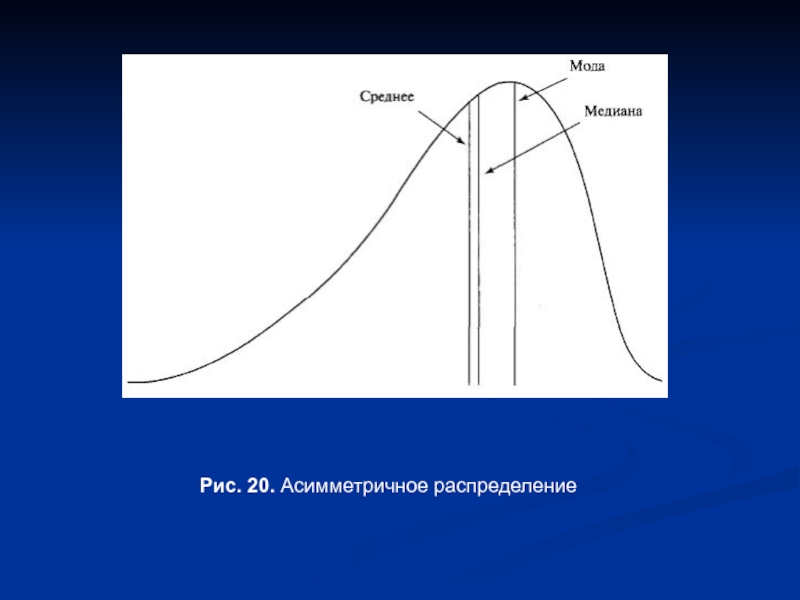
- 20. Рис. 20. Асимметричное распределение
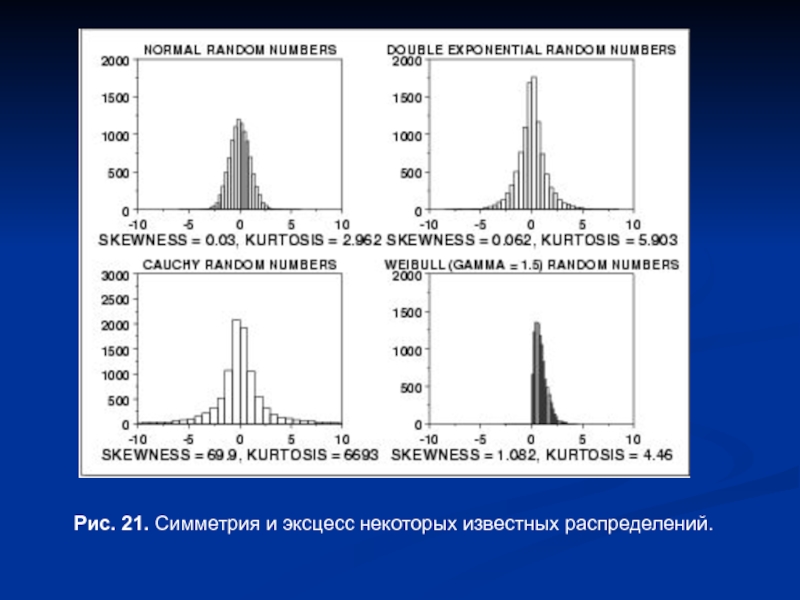
- 21. Рис. 21. Симметрия и эксцесс некоторых известных распределений.
Слайд 2ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1.1 Распределения случайные величины
1.2 Характеристики распределений
1.2.1 Математическое ожидание (среднее арифметическое)
1.2.2 Медиана и мода
1.2.3 Квартили и квантили
1.2.4 Дисперсия
1.2.5 Моменты
1.2.6 Гистограмма
1.2.7 Моменты многомерной случайной величины
1.3 Функции от случайных величин
1.4 Характеристические функции
Слайд 3Рис. 1. Распределение вероятностей дискретной случайной величины, f(x) (а) и функция
распределения
F(x) дискретной случайной величины (б).
Слайд 6Рис. 4. Распределения с одинаковой дисперсией, но с
разными математическими ожиданиями: μ=1
(1); 1,3 (2) и
2,3 (3).
Пусть
2,3 (3).
Пусть
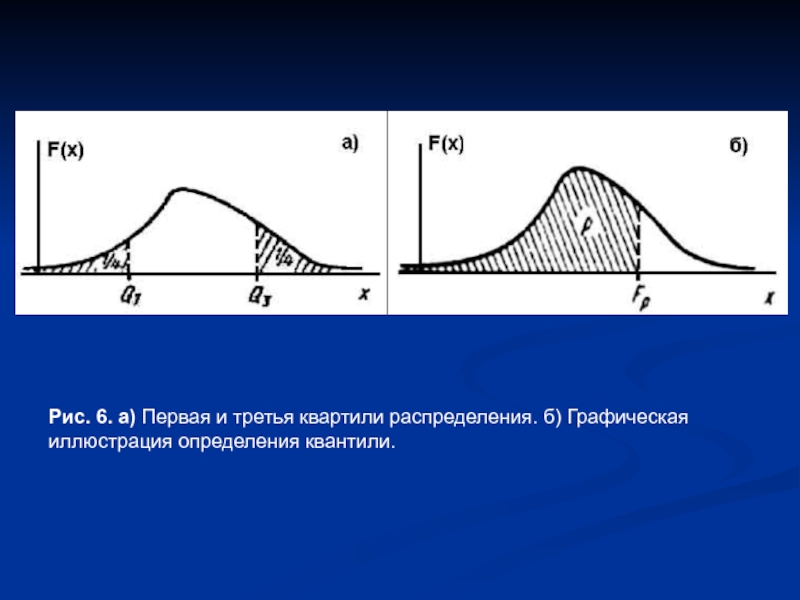
Слайд 8Рис. 6. а) Первая и третья квартили распределения. б) Графическая иллюстрация
определения квантили.
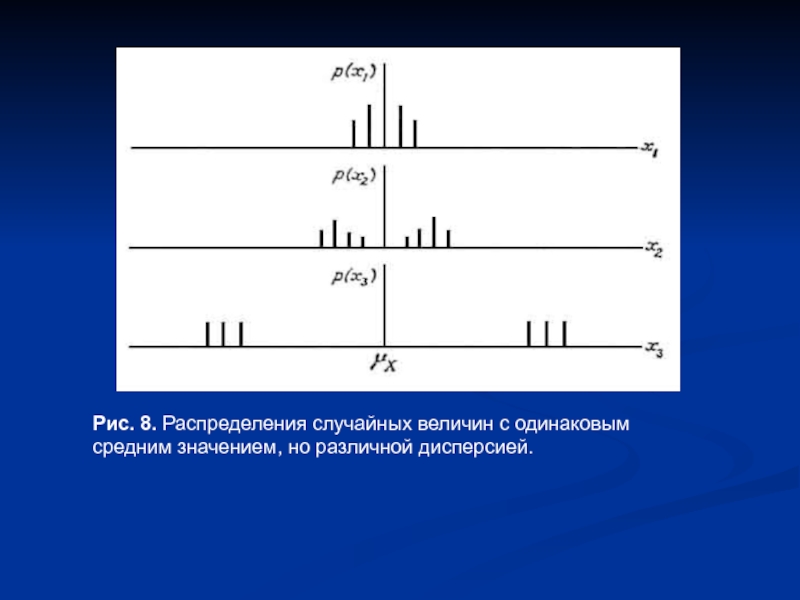
Слайд 10Рис. 8. Распределения случайных величин с одинаковым средним значением, но различной
дисперсией.
Слайд 11Рис. 9. Распределение с одинаковым математическим
ожиданием μ=0 и разными дисперсиями: σ=0,042
(3); 0,044 (2)
и 0,049 (1).
и 0,049 (1).
Слайд 15Рис. 15. Примеры Leptokurtic распределения: Лапласа, Логистическое, пример Mesokurtic распределения: нормальное
распределение, пример
Platykurtic распределения: однородное (непрерывное или дискретное)
Platykurtic распределения: однородное (непрерывное или дискретное)
Слайд 18Рис. 16. Положительная и отрицательная асимметрия распределения.
Рис. 17. Распределения с различным
эксцессом.