Методы оптимизации технических объектов. (Тема 3) презентация

ОПРЕДЕЛЕНИЯ

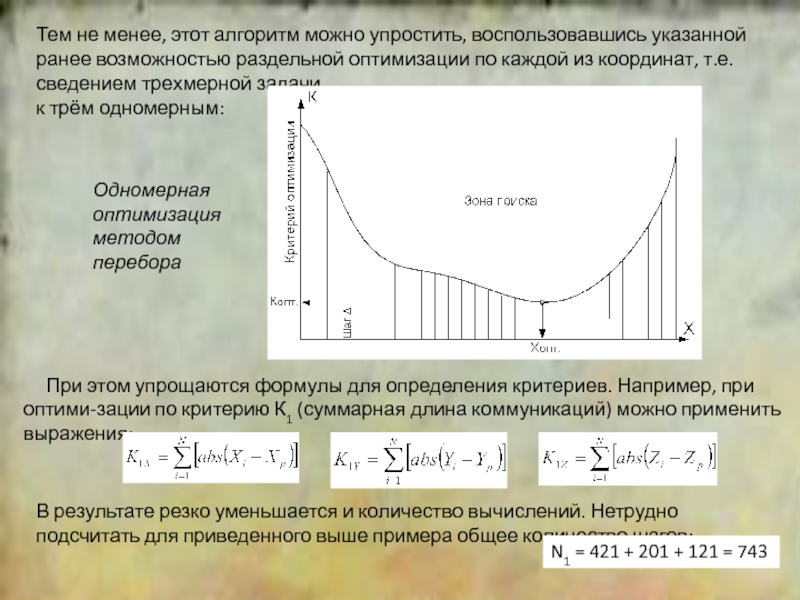
Одним из типовых приёмов системного анализа является представление исследуе-мого объекта в виде кибернетической системы, называемой «чёрным ящиком»:

Входные параметры,
характеризующие
воздействие на объект,
принято называть
факторами

Параметры, характеризу-
ющие реакцию объекта
на изменения факторов,
принято называть
откликами

Если речь идёт о технических объектах, факторами являются проектные параметры объекта, которые мы можем изменять, стремясь улучшить качество объекта: размеры, конфигурацию и взаимное расположение деталей, свойства конструкционных материалов и рабочих сред, режимные параметры и т.п.).

В качестве откликов мы будем рассматривать функциональные параметры,
характеризующие качество выполнения объектом заданного назначения.
Эти показатели называют критериями оптимизации.

предполагается изменять один из проектных параметров объекта − задача называется однопараметрической оптимизацией.
Если изменяемых параметров два и более − задача многопараметрическая.

Если в процессе оптимизации предполагается улучшать один показатель качества объекта − задача называется однокритериальной оптимизацией.
Если ставится задача параллельно улучшить несколько характеристик объекта − задача многокритериальная.

3.2. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ

Если задача однокритериальная, она формулируется следующим образом:
− найти такое сочетание значений варьируемых факторов (y1*, Y2*, . . . Yк*), которое
обеспечивает максимальное (или минимальное) значение критерия, т.е.

К→Кmax или К→Кmin

Выбор направления поиска оптимума зависит от физической природы критерия:
если это показатель, увеличение которого желательно (например, удельная мощность,
коэффициент полезного действия и т.п.), выбирается движение к максимуму, если
желательно уменьшение показателя (например, масса, стоимость, виброактивность), то
выбирается движение к минимуму.

Если задача многокритериальная, то точного математического решения она, как
правило, не имеет в связи с противоречивостью критериев. Речь может идти только о поиске и обосновании компромиссного решения.

выражается качественной мерой, необходимо специальное кодирование.
Факторы должны быть управляемыми, т.е. значения факторов должны подчиняться воле лица, выполняющего оптимизацию. Если все факторы являются управляемыми - можно проводить активную оптимизацию.
Факторы должны быть совместимыми – т.е. никакое из запланированных сочетаний значений факторов не должно приводить к аварии объекта, опасности для персонала, заражению окружающей среды и т.п., а также к физически нереальным значениям параметров объекта.
Факторы должны быть независимы друг от друга.

Последнее указание требует некоторых пояснений:
Допустим, мы имеем дело с машиной, рабочий процесс которой осуществляется с помощью порции газа массой G, химический состав которого определяется коэффициентом R. Можем ли мы добиваться улучшения характеристик машины путём одновременного воздействия на 3 термодинамических параметра газа:
объём V, давление P и абсолютную температуру T?
Люди, не знакомые с основами термодинамики газов, могут ответить: почему бы и нет? Но мы-то с Вами, разумеется, знаем об уравнении Менделеева-Клапейрона, связывающего эти параметры:
P∙V = G∙R∙T
Из него следует, что задав два из указанной тройки параметров, третий мы получим в строгом соответствие с этим уравнением, поэтому число произвольно варьируемых факторов для этой порции газа не может быть больше двух.

оптимизации обратимся за советом к Иоганну
Вольфгангу Гёте, которому принадлежит такая
мудрая фраза: «Суха теория, мой друг, но древо
жизни пышно зеленеет!»
Исходя из этого, будем рассматривать методики
оптимизации применительно к конкретным
практическим примерам.

4.1 О методологии
В этом разделе речь будет идти о методах, представленных в левой части
классификации, приведённой на предыдущем слайде.

4.2 Описание объекта оптимизации
Объект оптимизации - техническая система с центрально-лучевой топологией, т.е. состоящая из одного распределителя и нескольких потребителей, соединенных с рас-пределителем индивидуальными коммуникациями.

Возможные виды оборудования и коммуникаций

в производственном помещении, имеющем форму параллелепипеда длиной L, шириной B и высотой H.
Коммуникации состоят из прямолинейных участков, параллельных продольной (X), поперечной (Y) и вертикальной (Z) осям координат, и не имеют петель:

Условные обозначения:
Р – центральный распределитель;
П – потребители.

Габаритные размеры помещения:
длина L= 42 м; ширина B = 20 м; высота H =12 м

4.3 Формулировка цели оптимизации

Целью оптимизации является поиск наилучшего
расположения распределителя, при котором
минимальна суммарная длина коммуникаций
(критерий К1), суммарная масса коммуникаций
(критерий К2) или суммарная стоимость
коммуникаций (критерий К3).

Кроме того, может быть выполнена комплексная
оптимизация, учитывающая все три критерия.
Заданная точность оптимизации – 0,1 м
(по всем координатам).

мы уже выяснили, оптимизация заключается в поиске условий, при которых
критерий оптимизации достигает экстремального (максимального или минимального)
значения.
Поиск координаты экстремума является вполне тривиальной математической задачей.
Её аналитическое решение заключается в том, что, если известна функция, описывающая
зависимость исследуемого критерия от варьируемого параметра К = f(X), нужно эту
функцию продифференцировать, приравнять производную нулю и,
решив полученное уравнение, найти искомое значение параметра Х*.

Однако, эта операция возможна только в том случае, если функция К = f(X) является
дифференцируемой на всё интервале определения параметра Х. Для этого она должна
быть «гладкой», т.е. не иметь разрывов и перегибов. Увы, в рассматриваемом примере
она таковой не является (позже Вы это увидите, а пока просто примите на веру).

 

Что же делать в этом случае? А в этом случае придётся перейти к дискретному способу решения задачи, который принято называть математическим экспериментом.

4.5 Особенности дискретного поиска оптимального расположения распределителя

Алгоритм оптимизации должен предусматривать дискретное изменение координат распределителя, т.е. имитацию его перемещения в заданных габаритах пространства в соответствии с выбранным способом оптимизации.

от положения распределителя позволяет применить принцип суперпозиции, т.е. разбить трёхмерную задачу на три одномерных: - сначала выполнить продольный этап оптимизации, изменяя координату распределителя Xp, затем двигать распределитель поперек и по вертикали. В результате будет получена тройка координат, определяющая оптимальное положение распределителя.

На каждом шаге следует вычислять критерии оптимизации. Поскольку все участки коммуникаций параллельны осям координат и петли отсутствуют, можно применить следующие формулы:

где: К1 – суммарная длина коммуникаций (м);
К2 – суммарная масса коммуникаций (кг);
К3 – суммарная стоимость коммуникаций ($);
N – количество потребителей;

i – му потребителю (кг/м);
сi – удельная стоимость коммуникации к i – му потребителю ($/м);
Xi , Yi , Zi – координаты i – го потребителя (м);
Xp , Yp , Zp – координаты распределителя (м).

4.6 Выбор методов дискретной (экспериментальной) оптимизации
Рассмотрим особенности применения методов, представленных в левой части классификации (см. слайд 4).

4.6.1 Метод перебора

Суть метода заключается в том, что на факторное пространство, в котором производится поиск оптимума, накладывается сетка с заданным шагом, определяются значения критерия оптимизации в каждом из узлов сетки
и оптимальным сочетанием значений факторов считаются координаты узла, давшего наилучшее значение критерия.

Преимуществом такого приёма является возможность уменьшать риск пропуска оптимума за счёт регулирования шага сетки.

координаты помещения). Если рассмотреть заданный вариант габаритов помещения (L=42м; B=20м; H=12м), то нетрудно подсчитать, что для шага сетки по всем координатам Δ=0,1м (в соответствии с заданной точностью) общее число узлов сетки (а следовательно, и количество определений соответствующих значений критериев оптимизации) будет равно:

Недостатком метода перебора является большое количество процедур
определения числовых значений критериев оптимизации.

N = 421×201×121 = 10 239 141

Понятно, что для экспериментальной оптимизации с использованием натурных объектов или их физических моделей такой способ мало пригоден.

Однако в данной задаче речь идет о математическом эксперименте. Учитывая быстро-действие современных ПЭВМ, в принципе можно организовать эти вычисления с помощью достаточно несложной программы. Определённые технические трудности с выделением необходимого объема памяти могут возникнуть при попытке сохранения всего массива данных для последующего анализа. Однако для решения именно оптими-зационной задачи нет необходимости разделять оптимизацию на 2 этапа: формирование массива и поиск наилучшего узла. Эти процедуры вполне можно совместить, если выделить две ячейки памяти (для хранения номера узла и соответствующего значения критерия) и обновлять их содержимое всякий раз, когда вычисленное значение критерия окажется лучшим, чем предыдущего.

раздельной оптимизации по каждой из координат, т.е. сведением трехмерной задачи
к трём одномерным:

Одномерная
оптимизация
методом
перебора

При этом упрощаются формулы для определения критериев. Например, при оптими-зации по критерию К1 (суммарная длина коммуникаций) можно применить выражения:

В результате резко уменьшается и количество вычислений. Нетрудно подсчитать для приведенного выше примера общее количество шагов:

N1 = 421 + 201 + 121 = 743

специальные методы, предусматривающие минимизацию числа процедур при поиске оптимума.

4.6.2 Метод половинного деления

Идея метода заключается в том, что оптимизация выполняется рядом последовательных дискретных этапов:
− весь диапазон изменения параметра Х делят пополам;
− в каждой из половин определяют среднюю точку и вычисляют или экспериментально определяют для этих точек значения критерия оптимизации;
− ту половину, в середине которой значение критерия оказалось хуже, отбрасывают, уменьшая, таким образом, ширину зоны поиска в 2 раза.

Процедуры деления повторяют до тех пор, пока ширина зоны поиска не станет меньше заданной точности оптимизации

Для заданного примера поиск оптимума
с точностью до 0,1 м. потребовал 10 шагов
в продольном направлении, 8 шагов в
поперечном направлении и 7 шагов в
вертикальном направлении, т.е. всего
25 шагов для одного критерия.
Для оптимизации по всем трём критериям
потребуется 75 шагов:

оптимуму, поскольку уменьшение ширины зоны поиска определяется степенной функцией 2n , где n – число шагов.

Недостатком метода является возможность сбоя при наличии в зоне поиска нескольких минимумов (или максимумов) критерия. В этом случае метод не гарантирует выход на самый меньший из минимумов (или самый больший из максимумов).

4.6.3 Метод Фибоначчи (золотого сечения)

Так же, как и метод половинного деления, этот метод предусматривает пошаговое сужение зоны поиска оптимума, только на каждом шаге зону надо делить не пополам,
а в пропорции «золотого сечения» (0,618 : 0,382).

Кстати, с «золотым сечением» связано много удивительного − покопайтесь в Интернете.
А я прощаюсь с Вами до следующей недели. А. Равин

Итальянским учёным Фибоначчи было доказано, что именно такой способ деления диапазона поиска обеспечивает самый быстрый выход к оптимуму. В этом состоит преимущество данного метода.

Недостаток − тот же, что и у метода половинного деления.