- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методика оценки организационной структуры управления организации презентация
Содержание
- 1. Методика оценки организационной структуры управления организации
- 2. 1. Методика оценки организационной структуры организации
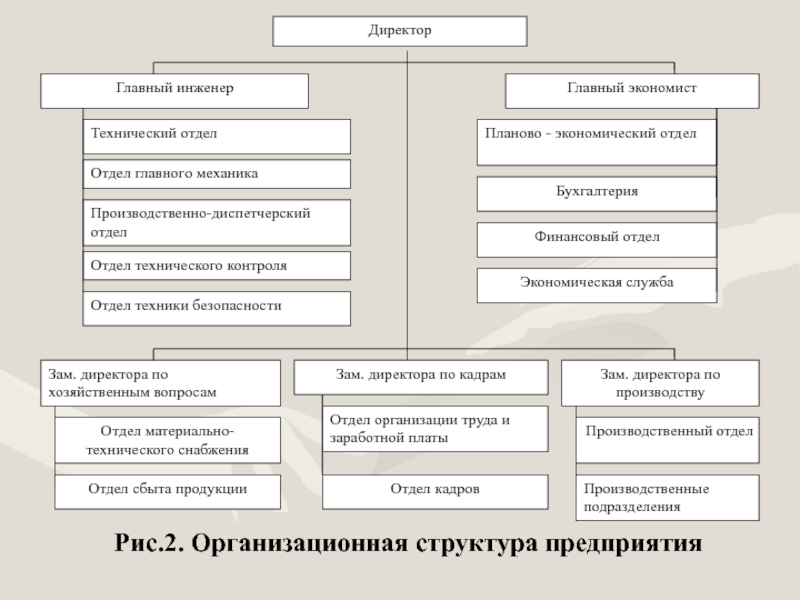
- 3. Рис.2. Организационная структура предприятия
- 4. Аппарат управления предприятием построен таким образом, что
- 5. Граф G, соответствующий данному предприятию, показан на
- 6. a ij = 1 – при наличии
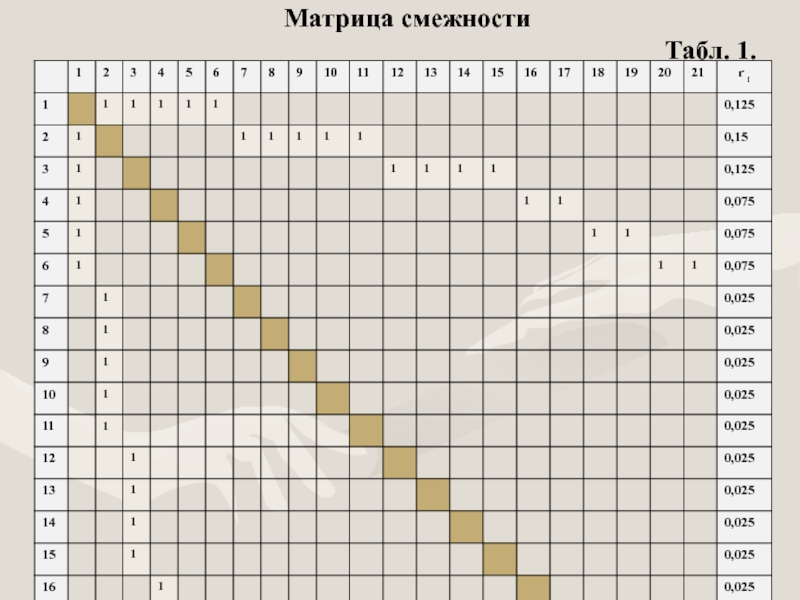
- 7. Матрица смежности
- 8. 1. По матрице смежности определим ранг каждого
- 9. 2. Проверим связность структуры. Для связных
- 10. 3. Проведем оценку структурной избыточности R, отражающей
- 11. Данная характеристика является косвенной оценкой экономичности и
- 12. 4. Определим структурную компактность структуры Q,которая отражает
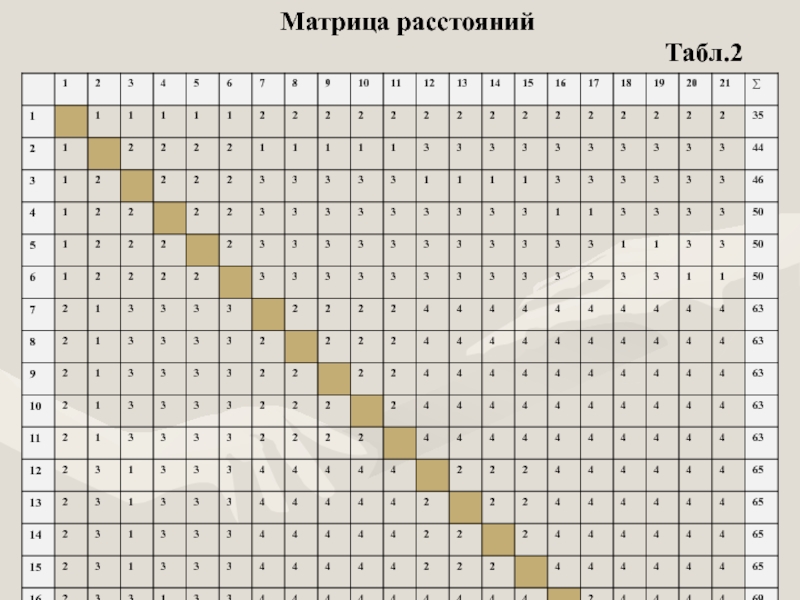
- 13. Матрица расстояний
- 14. По таблице определяем – Q = 1264.
- 15. Структурную компактность можно характеризовать и другой характеристикой
- 16. 5. Для характеристики степени централизации системы используется
- 17. Для нашего случая, высокое значение степени центральности
Слайд 21. Методика оценки организационной структуры организации
При проведении структурного анализа систем очень
Целесообразность определения таких характеристик состоит в том, что уже на ранних стадиях проектирования организаций появляется необходимость оценивать качество структуры проектируемой организации и ее элементов с позиций системного анализа, а также сравнивать различные предлагаемые варианты организационных структур между собой.
Например:
Предприятие является открытым акционерным обществом, относится к электротехнической промышленности и производит светотехническое оборудование для автомобильной промышленности. Численность персонала предприятия на конец 2009 года составляла 3045 человек. Организационная структура предприятия представлена на рис.2
Слайд 4Аппарат управления предприятием построен таким образом, что бы обеспечить в техническом,
Предварительный анализ показывает, что на предприятии применена линейно-функциональная структура управления. При этом, каждый структурный элемент выполняет конкретные задачи и обладает определенными правами и обязанностями.
Для проведения структурного анализа организационной структуры предприятия представим ее в виде
графа G = {X, U},
где :
X - множество вершин (|X | = n), соответствующее множеству структурных элементов;
U - множество ребер (|U| = m), соответствующее множеству связей между структурными элементами предприятия.
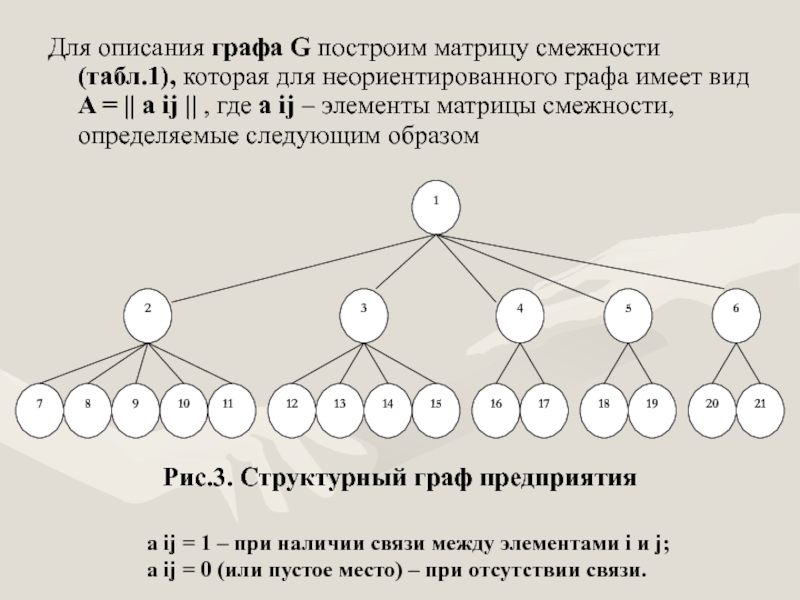
Слайд 5Граф G, соответствующий данному предприятию, показан на рис.3, где цифры обозначают:
1 – директор;
2 – главный инженер;
3 – главный экономист;
4 – зам. директора по хозяйственным вопросам;
5 – зам. директора по кадрам;
6 – зам. директора по производству;
7 – технический отдел;
8 – отдел главного механика;
9 – производственно-диспетчерский отдел;
10 – отдел технического контроля;
11 – отдел техники безопасности;
12 – планово - экономический отдел;
13 – бухгалтер;
14 – финансовый отдел;
15 – экономическая служба;
16 – отдел материально-технического снабжения;
17 – отдел сбыта;
18 – отдел организации труда и заработной платы;
19 – отдел кадров;
20 – производственный отдел;
21 – производственные подразделения.
Слайд 6a ij = 1 – при наличии связи между элементами i
Для описания графа G построим матрицу смежности (табл.1), которая для неориентированного графа имеет вид A = || a ij || , где a ij – элементы матрицы смежности, определяемые следующим образом
Рис.3. Структурный граф предприятия
Слайд 81. По матрице смежности определим ранг каждого элемента
Для
Чем выше ранг элемента, тем более сильно он связан с другими элементами и тем более тяжелыми будут последствия при качества его функционирования. В нашем случае наиболее высокий ранг (0,15) имеет второй элемент структуры (главный инженер).
Слайд 92. Проверим связность структуры.
Для связных структур (не имеющих обрывов и
Правая часть неравенства определяет необходимое минимальное число связей в структуре графа, содержащего n вершин.
Для нашего случая n (количество структурных элементов) равно 21 и условие ½ • 40 ≥ 21 – 1, выполняется , то есть структура является связной.
Слайд 103. Проведем оценку структурной избыточности R, отражающей превышение общего числа связей
где m – множество ребер графа (1/2 количества связей в матрице смежности;
n – количество вершин (элементов) структуры.
где a ij – элементы матрицы смежности.
Слайд 11Данная характеристика является косвенной оценкой экономичности и надежности исследуемой структуры и
Если R< 0, то система несвязная;
R = 0, система обладает минимальной избыточностью;
R > 0, система имеет избыточность;
чем выше R, тем выше избыточность.
Для нашего случая R = ½ • 40 • 1/(21-1) – 1 = 0, то есть структура имеет минимальную избыточность.
Слайд 124. Определим структурную компактность структуры Q,которая отражает общую структурную близость элементов
где d ij – расстояние от элемента i до элемента j, то есть минимальное число связей, соединяющих элементы i и j.
Для определения величины общей структурной компактности построим матрицу расстояний
D = || d ij || - (табл.2).
Слайд 14По таблице определяем – Q = 1264.
Однако для количественной оценки структурной
где Q min = n (n-1) – минимальное значение компактности для структуры типа “полный граф” (каждый элемент соединен с каждым).
Для нашей структуры Q min =21· (21 – 1) = 420.
Тогда Qотн = 1264/420 – 1 = 2,01.
Слайд 15Структурную компактность можно характеризовать и другой характеристикой – диаметром структуры:
равным максимальному значению расстояния d ij в матрице расстояний. Для нашей структуры d = 4.
С увеличением Qотн и d увеличиваются средние временные задержки при обмене информацией между подразделениями, что вызывает снижение общей надежности. С этой точки зрения структура исследуемого предприятия имеет надежность среднего уровня (максимальную надежность имеет с полный граф, для которой Qотн =0, а d =1).
Слайд 165. Для характеристики степени централизации системы используется показатель центральности структурного элемента,
Чем меньше удален i- й элемент от других, тем больше его центральность и тем большее количество связей осуществляется через него. В нашем случае наиболее центральным является первый элемент (директор), для которого ∑ d ij = 35 = min, то есть он обладает максимальным коэффициентом центральности
Z max = 1264 / (2 · 35) = 18, 06
Степень центральности в структуре в целом может быть охарактеризована индексом центральности:
Значение степени центральности находится в диапазоне 1 ≥ δ ≥ 0,
при этом для структур с равномерным распределением связей δ = 0,
для структур, имеющих максимальную степень централизации δ = 1.
Слайд 17Для нашего случая, высокое значение степени центральности структуры (δ = 0,88)
Если в структуре есть центральный элемент, т.е. δ близко к 1, то целесообразно продумать меры по дублированию данного центрального элемента для повышения надежности структуры организации.