- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
8. Управление запасами презентация
Содержание
- 1. 8. Управление запасами
- 2. Концепция логистического подхода к управлению запасами
- 3. Более подробное рассмотрение движения материальных и информационных
- 4. Запасы представляют собой вторую по значимости после
- 5. Запасы относятся к типу объектов, требующих
- 6. Исследование логистической системы управления запасами (ЛСУЗ) отвечает
- 7. Каковы общие уровни запасов на данном
- 8. Суть концепции управления запасами во взаимосвязи ЛСУЗ
- 9. Критерий оптимальности Критерием оптимизации запасов как правило
- 10. Виды запасов Запасы сырья, материалов, комплектующих
- 11. Классификация во времени позволяет выделять различные
- 12. Системы управления запасами и условия их применимости
- 13. Способы решения поставленных задач определяются в зависимости
- 14. Условие применимости: Применение основных СУЗ возможно только
- 15. Модели управления запасами (МУЗ) Для решения
- 16. Обобщенная модель управления запасами Природа задачи
- 17. Ответ на первый вопрос определяет экономичный размер
- 18. Модели управления запасами классифицируются как статические
- 19. Изменение уровня запаса δ (t) во времени
- 20. dкр – уровень запасов, соответствующий точке
- 21. Однопродуктовая статическая модель управления запасами Эта
- 22. Введем обозначения: δ - объем заказа
- 23. Изменение уровня запаса при постоянной интенсивности спроса
- 24. Для построения функции затрат требуется два стоимостных
- 25. Суммарные затраты в единицу времени TCU (“Total
- 26. Решение Решение описанной выше математической модели можно
- 27. Предполагая, что δ является непрерывной переменной, получаем
- 28. Отсюда оптимальное значение размера запаса определяется выражением,
- 29. Оптимальная стратегия управления запасами для рассмотренной модели
- 30. Пример 1. Еженедельный спрос на товар составляет
- 31. Решение с помощью формул
- 32. В действительности пополнение запаса не может произойти
- 33. Пусть t1=15 нед.
- 34. Если t1 > t*, то определяем эффективный
- 35. Пусть t1 = 22 недели, тогда возобновление
- 36. δкр
- 37. Однопродуктовая статическая модель с «разрывами» цен
- 38. Следовательно, затраты на приобретение продукции в единицу времени равны:
- 39. Учтем затраты на приобретение продукции и задача управления запасами будет иметь вид:
- 40. Решение Решение описанной выше математической модели можно
- 41. Так как функции F1(d) и F2(d) отличаются
- 42. y δm затраты F2 F1
- 43. График функции затрат F(y), если идти от
- 44. и определяется следующим образом:
- 46. Пример Автомобильная мастерская специализируется на быстрой замене
- 47. Многопродуктовая статическая модель управления запасами с ограничениями на емкость склада См. методичку.
Слайд 2Концепция логистического подхода к управлению запасами
С позиций логистики процесс производства
Слайд 3Более подробное рассмотрение движения материальных и информационных потоков в рамках отдельного
Предметы труда как перед, так и после каждого этапа обработки сосредотачиваются в виде запасов.
Таким образом запас – это форма существования МП.
Слайд 4Запасы представляют собой вторую по значимости после обработки составляющую производственного процесса.
Именно запасы сырья, материалов, комплектующих и готовой продукции непосредственно увязывают организацию с ее поставщиками и потребителями, формируя цепи логистической системы экономики в целом.
Слайд 5
Запасы относятся к типу объектов, требующих больших капиталовложений
Следовательно, это один
Слайд 6Исследование логистической системы управления запасами (ЛСУЗ) отвечает на следующие вопросы:
Какой уровень
В чем состоит компромисс между уровнем обслуживания потребителя и уровнем запасов в логистической системе?
Какие объемы запасов должны быть созданы на каждой стадии логистического и производственного процессов?
Слайд 7
Каковы общие уровни запасов на данном предприятии связаны со специфическим уровнем
Каково значение компромисса между выбранным способом транспортировки и запасами?
Как меняются затраты на содержание запасов в зависимости от числа складов?
Слайд 8Суть концепции управления запасами во взаимосвязи ЛСУЗ с производством.
Практическая реализация
Сущность концепции УЗ
Слайд 9Критерий оптимальности
Критерием оптимизации запасов как правило являются суммарные издержки на пополнение
Слайд 10Виды запасов
Запасы сырья, материалов, комплектующих и готовой продукции представляют собой
Критериями классификации запасов могут быть два параметра движения МП – пространство (местонахождение) и время, а также функция запаса.
Слайд 11
Классификация во времени позволяет выделять различные количественные уровни запасов (рисунок А).
Классификация
Слайд 12Системы управления запасами и условия их применимости
Реализация логистической системы управления
определение характера спроса (статический или динамический, вероятностный – детерминированный);
учет текущего уровня запасов;
определение размеров гарантийного запаса;
расчет размера запаса;
определение интервала времени между поставками.
Слайд 13Способы решения поставленных задач определяются в зависимости от характера спроса и
Основными СУЗ являются следующие :
СУЗ с фиксированным размером заказа.
СУЗ с фиксированным интервалом времени между запасами.
СУЗ с установленной периодичностью пополнения запасов и меняющимся размером заказа.
Слайд 14Условие применимости:
Применение основных СУЗ возможно только когда отклонения от запланированных показателей
В более сложных случаях управление запасами используются другие СУЗ, элементами которых являются основные СУЗ.
Слайд 15Модели управления запасами (МУЗ)
Для решения задач УЗ используются различные математические
Вид используемых моделей определяется характером спроса и ЛСУЗ.
Для решения моделей управления запасами используют линейное, нелинейное, динамическое, стохастическое программирование и другие методы оптимизации.
Слайд 16Обобщенная модель управления запасами
Природа задачи УЗ определяется неоднократным размещением и
С этой точки зрения стратегия управления запасами должна отвечать на следующие два вопроса:
Какое количество хранимого запаса следует заказать?
Когда заказывать?
Слайд 17Ответ на первый вопрос определяет экономичный размер заказа путем минимизации следующей
Все эти стоимости должны быть выражены как функции искомого объема заказа и интервала времени между заказами.
Ответ на второй вопрос “Когда заказывать?” зависит от типа системы управления запасами, с которой мы имеем дело.
Слайд 18
Модели управления запасами классифицируются как статические и динамические:
В статических моделях
В динамических моделях объем спроса является функцией времени.
Слайд 19Изменение уровня запаса δ (t) во времени при переменном спросе и
dкр – уровень запасов, соответствующий точке заказа;
1 – точка заказа;
2 – точка получения заказа;
tg – время доставки.
Слайд 20
dкр – уровень запасов, соответствующий точке заказа;
1 – точка заказа;
2 – точка получения заказа;
tg – время доставки.
Слайд 21 Однопродуктовая статическая модель управления запасами
Эта модель характеризуется
постоянным во времени
мгновенным пополнением запаса (δ) и
отсутствием дефицита.
Слайд 22Введем обозначения:
δ - объем заказа (количество единиц продукции);
d - интенсивность
t0 - продолжительность цикла заказа или время расходования запаса (измеряется во временных единицах);
Продолжительность цикла заказа равна единиц времени.
Средний уровень запаса = единиц.
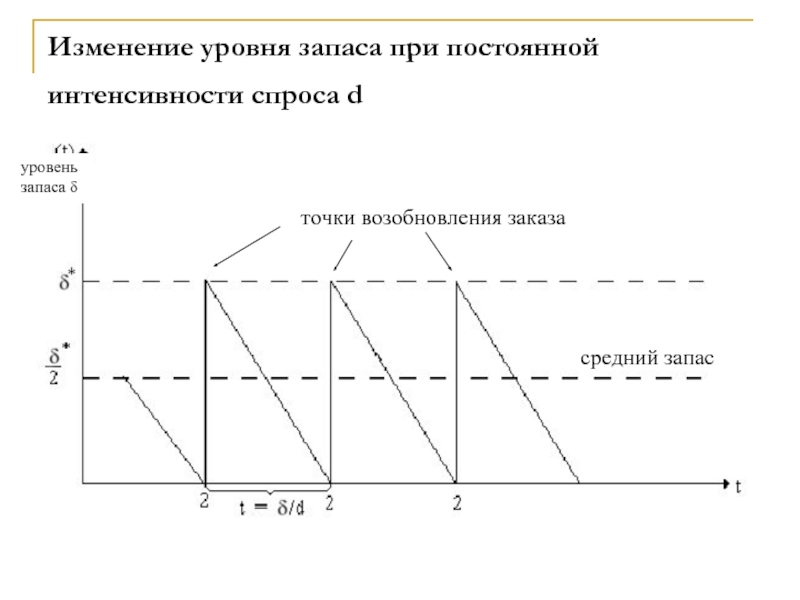
Слайд 23Изменение уровня запаса при постоянной интенсивности спроса d
запаса
уровень запаса δ
точки возобновления заказа
средний запас
Слайд 24Для построения функции затрат требуется два стоимостных параметра:
К – затраты на
h – затраты на хранение (затраты на единицу складируемой продукции в единицу времени).
Тогда затраты на пополнение запаса в единицах времени:
Затраты на хранение в единицах времени:
Слайд 25Суммарные затраты в единицу времени TCU (“Total Cost per Unit time”)
Окончательно однопродуктовая статитическая модель управления запасами будет иметь вид:
(δ >0)
Оптимальное значение объема заказа δ* определяется путем минимизации по δ функции F(δ).
Слайд 26Решение
Решение описанной выше математической модели можно реализовать с помощью надстройки «Поиск
Кроме того задача может быть решена с помощью формул выведенных далее.
Выбирайте любой удобный для вас способ.
Слайд 27Предполагая, что δ является непрерывной переменной, получаем необходимое условие минимума (
Так как TCU(y) – выпуклая, то данное условие является и достаточным.
Слайд 28Отсюда оптимальное значение размера запаса определяется выражением, называемым формулой Уилсона:
Оптимальные затраты
Слайд 29Оптимальная стратегия управления запасами для рассмотренной модели формулируется следующим образом:
заказывать единиц продукции
через каждые единиц времени.
Слайд 30Пример 1.
Еженедельный спрос на товар составляет 100 ед. Затраты на размещение
Слайд 32В действительности пополнение запаса не может произойти мгновенно в момент размещения
В этом случае точка возобновления заказа имеет место, когда уровень запаса опускается до
δкр = t1*d единиц.
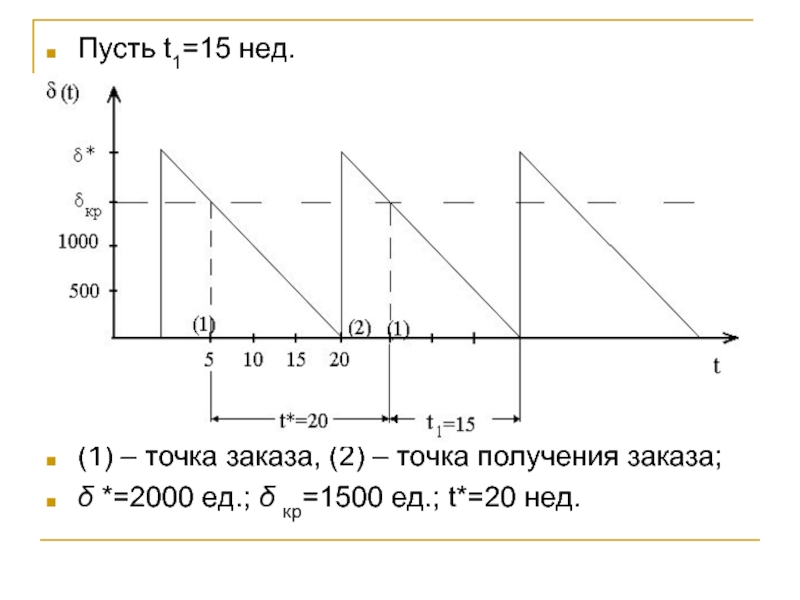
Слайд 33Пусть t1=15 нед.
(1) – точка заказа, (2) – точка получения заказа;
δ
Слайд 34Если t1 > t*, то определяем эффективный срок te выполнения заказа
,
где n – наибольшее целое, не превышающее .
Такое решение оправдывается тем, что после n циклов длиной t* ситуация управления запасами становится такой же, как если бы интервал между размещением одного заказа и получение другого был равен te. Следовательно, точка возобновления заказа имеет место при уровне запаса te·d единиц продукции, и стратегия управления запасами может быть переформулирована следующим образом: заказывать δ* единиц продукции, как только уровень запаса опускается до te·d единиц.
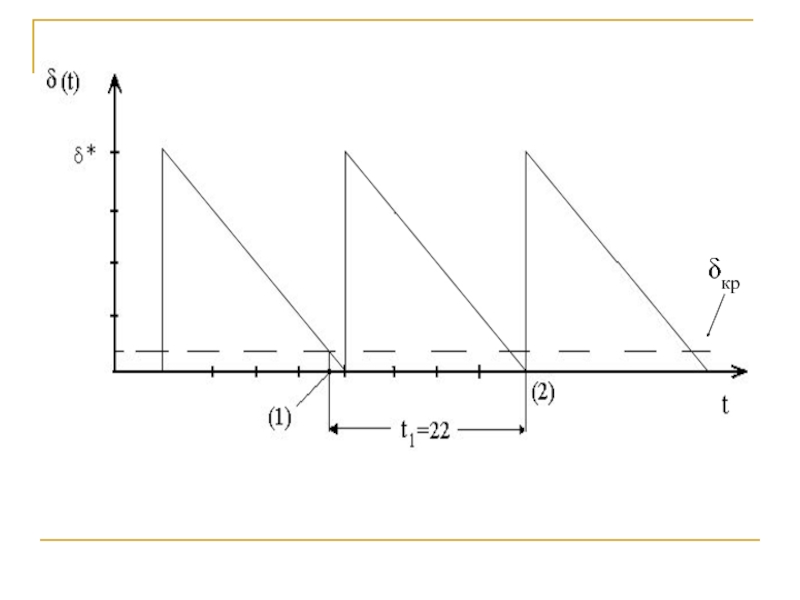
Слайд 35Пусть t1 = 22 недели, тогда возобновление заказа происходит когда уровень
Это возможно при стабилизации работы системы управления запасами. В этом случае в любой момент времени имеется более одного еще не выполненного заказа.
Слайд 37Однопродуктовая статическая модель с «разрывами» цен
Предположим, что продукция может быть
Таким образом, стоимость единицы продукции c определяется как
Слайд 40Решение
Решение описанной выше математической модели можно реализовать с помощью надстройки «Поиск
Кроме того задача может быть решена с помощью формул выведенных далее.
Выбирайте любой удобный для вас способ.
Слайд 41Так как функции F1(d) и F2(d) отличаются на постоянную величину, не
Слайд 43График функции затрат F(y), если идти от минимальных значений аргументов, совпадает
Решение задачи (δ *) будет зависеть от соотношения значений q, δmin и q1,
где q1 – решение уравнения
F1(δ min) = F2(q1); q1> δ min