- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
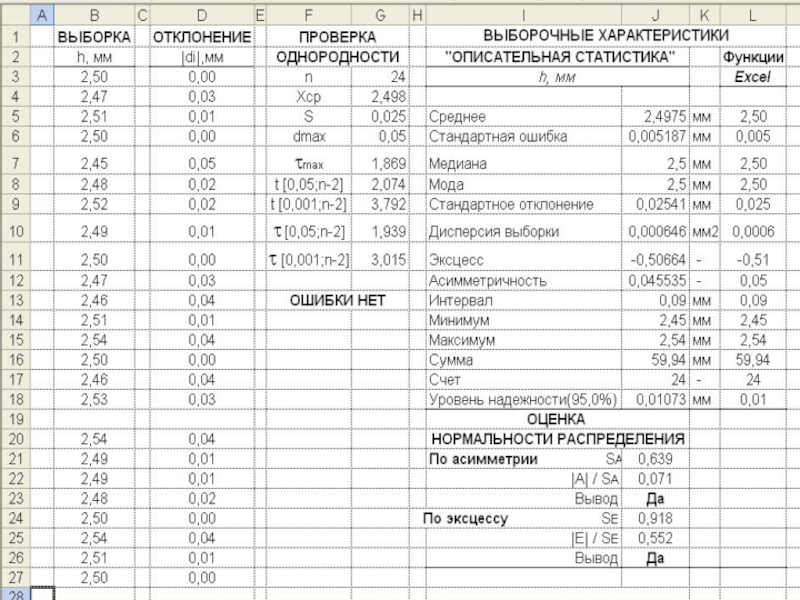
Стандартизованные методы обработки и анализа числовой информации презентация
Содержание
- 1. Стандартизованные методы обработки и анализа числовой информации
- 3. ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ Характеристики положения: Среднее выборочное
- 4. ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫБОРОЧНОГО ОЦЕНИВАНИЯ Обработка и анализ выборки. Построение выборочного распределения
- 5. ОБРАБОТКА И АНАЛИЗ ВЫБОРКИ
- 6. ЦЕЛИ ОБРАБОТКИ И АНАЛИЗА ВЫБОРКИ Выявление
- 8. ОЦЕНИВАНИЕ ИСТИННОГО ЗНАЧЕНИЯ Анализируемая случайная величина
- 9. ВЫВОД ОТНОСИТЕЛЬНО ИСТИННОГО ЗНАЧЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С
- 10. НЕОБХОДИМОСТЬ ПРОВЕРКИ ОДНОРОДНОСТИ Среди элементов выборки могут
- 11. АЛГОРИТМ ПРОВЕРКИ И ОБЕСПЕЧЕНИЯ ОДНОРОДНОСТИ
- 12. МЕТОДЫ ОЦЕНИВАНИЯ НОРМАЛЬНОСТИ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ по
- 13. АСИМЕТРИЯ И ЭКСЦЕСС НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ Асимметрия или
- 14. УСЛОВИЯ НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ ПО АСИММЕТРИИ И
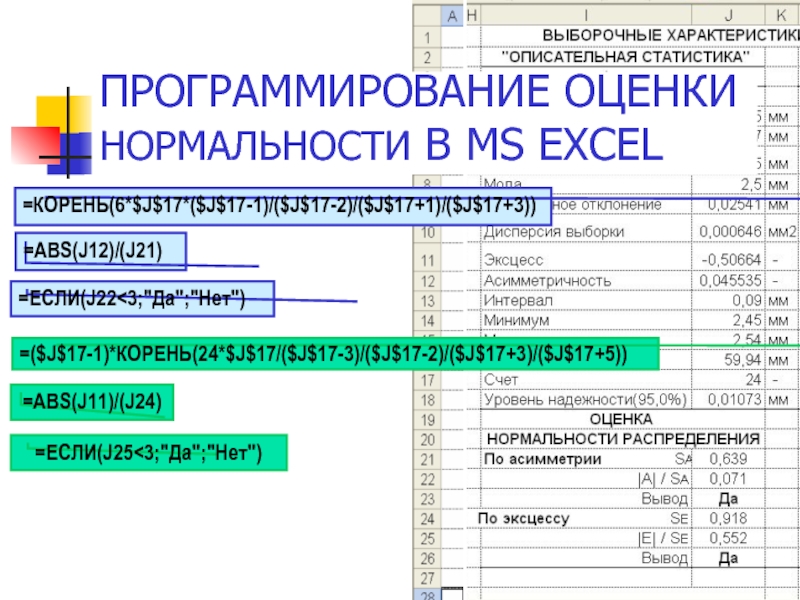
- 15. =КОРЕНЬ(6*$J$17*($J$17-1)/($J$17-2)/($J$17+1)/($J$17+3)) =ABS(J12)/(J21) =ЕСЛИ(J22
- 16. ВЫВОДЫ ОТНОСИТЕЛЬНО ТЕОРЕТИЧЕСКОЙ КРИВОЙ Отношение асимметрии (А=0,046)
- 17. ПОСТРОЕНИЕ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ
- 18. ПОСЛЕДОВАТЕЛЬНОСТЬ ПОСТРОЕНИЯ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ Построить вариационный
- 19. ПОСТРОЕНИЕ ВАРИАЦИОННОГО РЯДА Разбить интервал варьирования параметра
- 20. РАЗБИЕНИЕ ИНТЕРВАЛА ВАРЬИРОВАНИЯ НА КАРМАНЫ
- 21. ВАРИАНТА Значение случайной величины, которое считают характерным для j-го кармана
- 22. ТАБЛИЧНОЕ ПРЕДСТАВЛЕНИЕ ВАРИАЦИОННОГО РЯДА
- 23. ЧАСТОТА Число значений случайной величины, которые могут
- 24. ДИФФЕРЕНЦИАЛЬНАЯ ЧАСТОСТЬ (ЧАСТОСТЬ) Отношение частоты некоторого члена
- 25. КУМУЛЯТИВНАЯ ЧАСТОСТЬ Кумулятивная частость является выборочной оценкой
- 26. РАЗБИЕНИЕ ИНТЕРВАЛА НА КАРМАНЫ n
- 27. РАЗБИЕНИЕ ИНТЕРВАЛА НА КАРМАНЫ =МИН(B2:B25) =МАКС(B2:B25) =H3-G3 =I3/(F3-1) =1+3,322*LOG10(D3) С КЛАВИАТУРЫ С КЛАВИАТУРЫ
- 28. РАЗБИЕНИЕ ИНТЕРВАЛА НА КАРМАНЫ
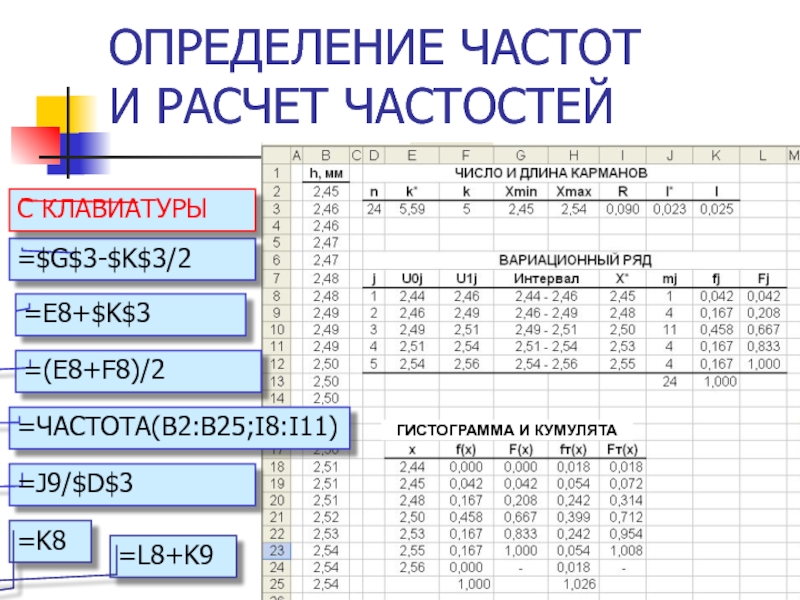
- 29. ОПРЕДЕЛЕНИЕ ЧАСТОТ И РАСЧЕТ ЧАСТОСТЕЙ
- 30. ОПРЕДЕЛЕНИЕ ЧАСТОТ И РАСЧЕТ ЧАСТОСТЕЙ =E8+$K$3 =(E8+F8)/2 =ЧАСТОТА(B2:B25;I8:I11) =J9/$D$3 =$G$3-$K$3/2 С КЛАВИАТУРЫ =K8 =L8+K9
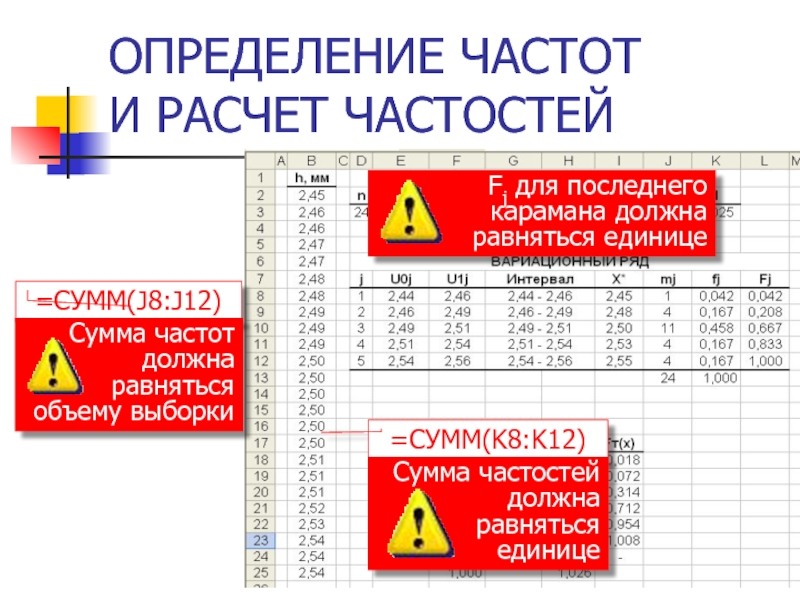
- 31. ОПРЕДЕЛЕНИЕ ЧАСТОТ И РАСЧЕТ ЧАСТОСТЕЙ Fj для последнего карамана должна равняться единице
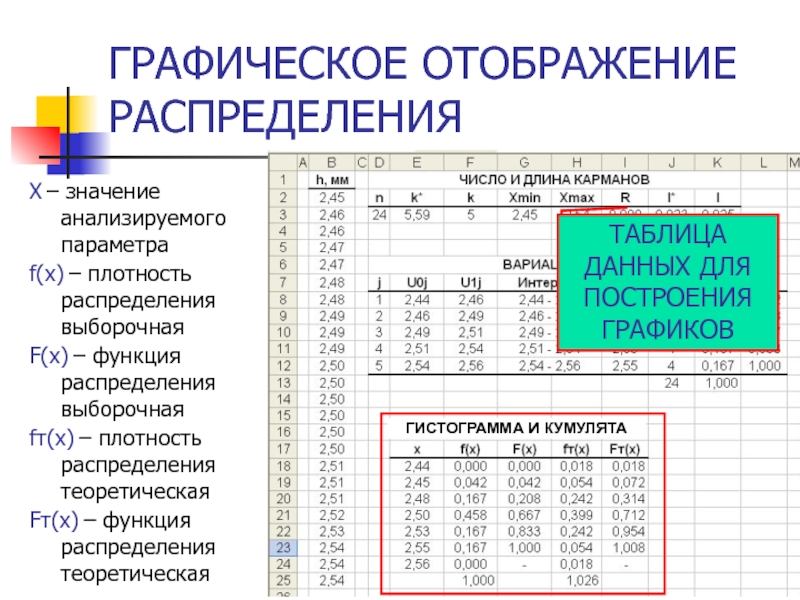
- 32. ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ Х – значение анализируемого
- 33. ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ =E8 =F12
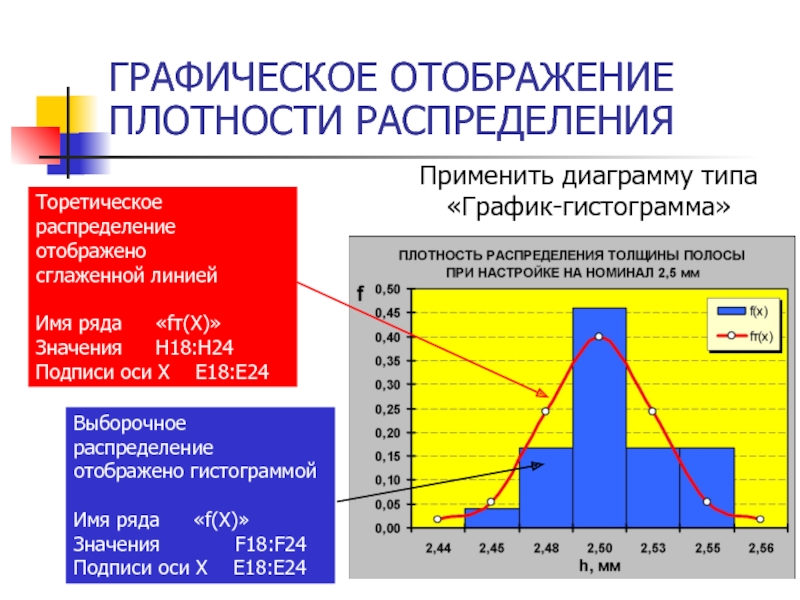
- 34. ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ Применить диаграмму типа «График-гистограмма»
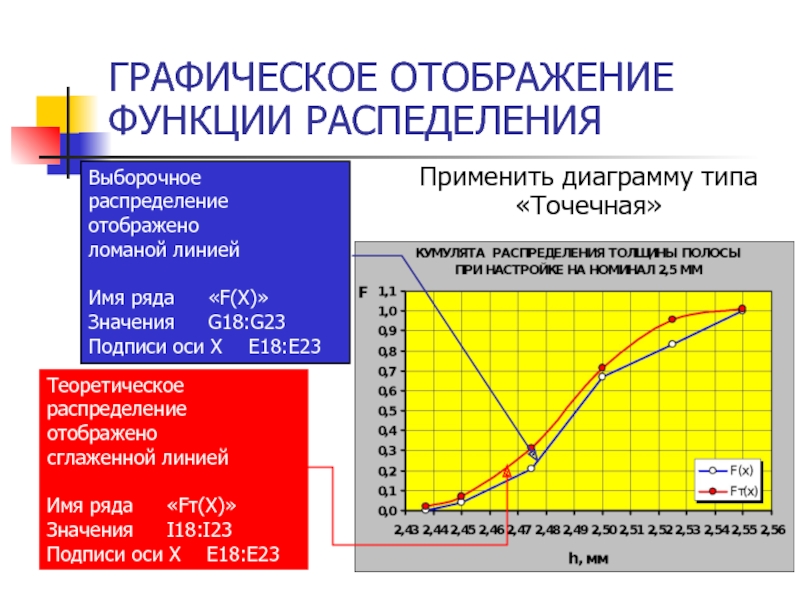
- 35. ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ ФУНКЦИИ РАСПЕДЕЛЕНИЯ Применить диаграмму типа «Точечная»
- 36. ВНЕШНИЕ ПРИЗНАКИ КАЧЕСТВА ВАРИАЦИОННОГО РЯДА
- 37. СООТНОШЕНИЕ ПРАВОЙ ГРАНИЦЫ ПОСЛЕДНЕГО КАРМАНА И Xmax
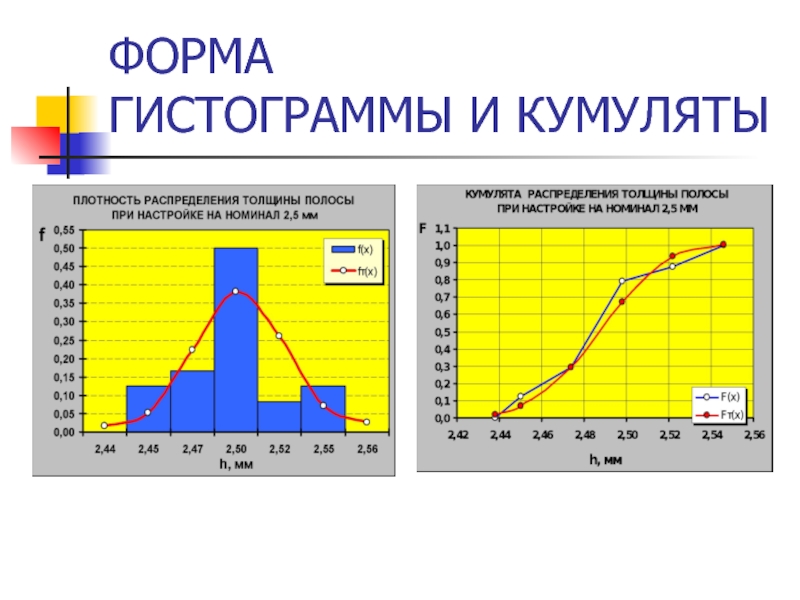
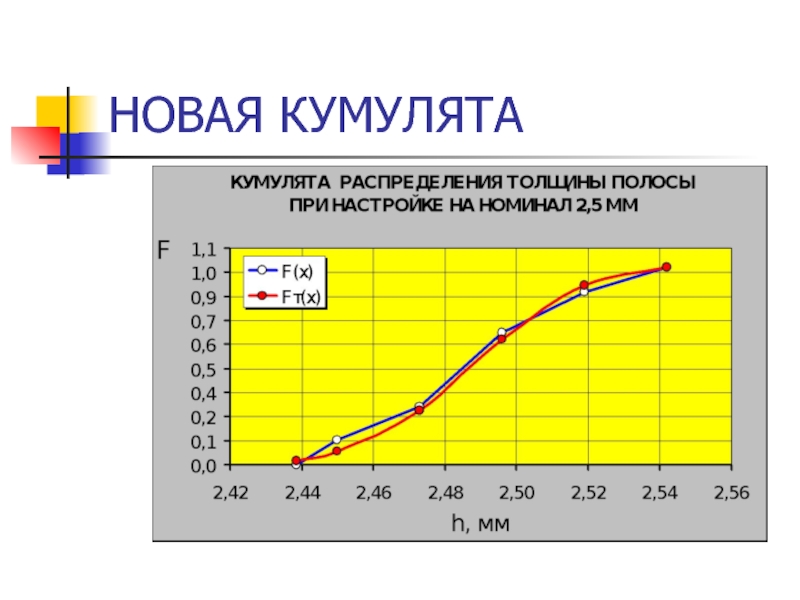
- 38. ФОРМА ГИСТОГРАММЫ И КУМУЛЯТЫ
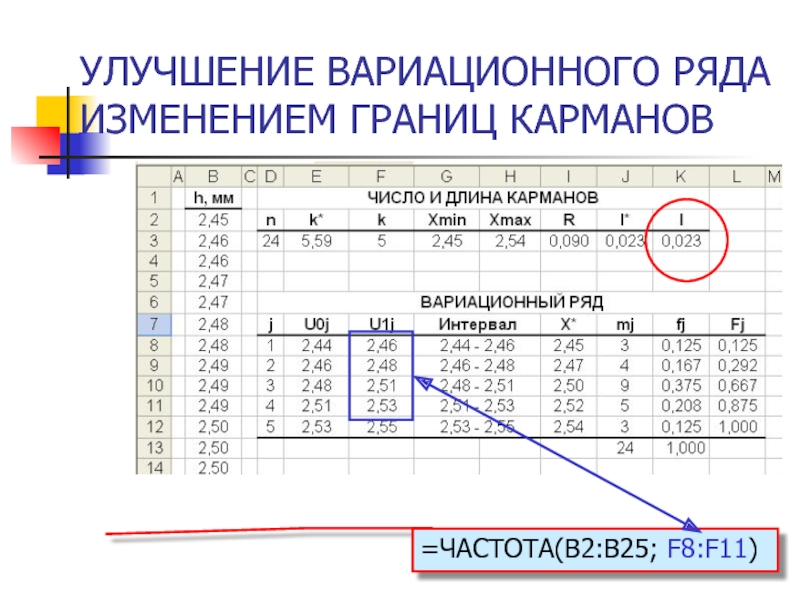
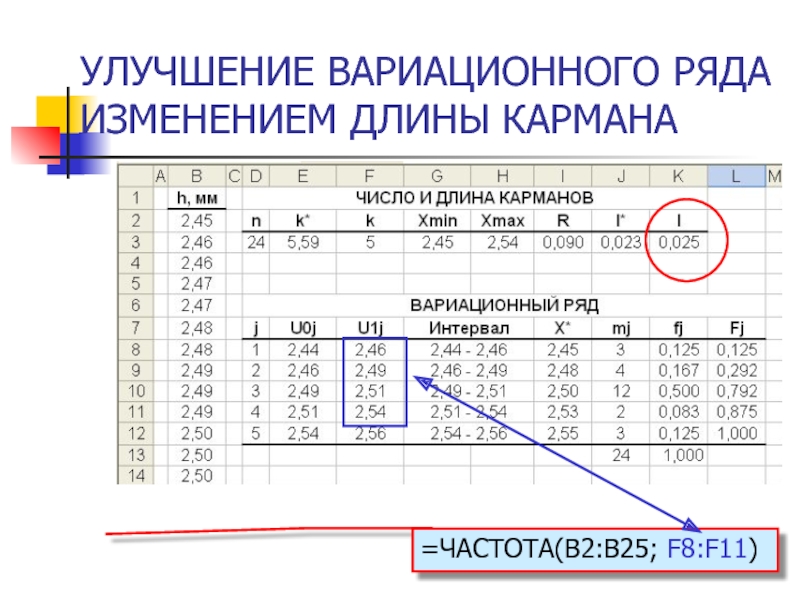
- 39. УЛУЧШЕНИЕ ВАРИАЦИОННОГО РЯДА ИЗМЕНЕНИЕМ ГРАНИЦ КАРМАНОВ =ЧАСТОТА(B2:B25; F8:F11)
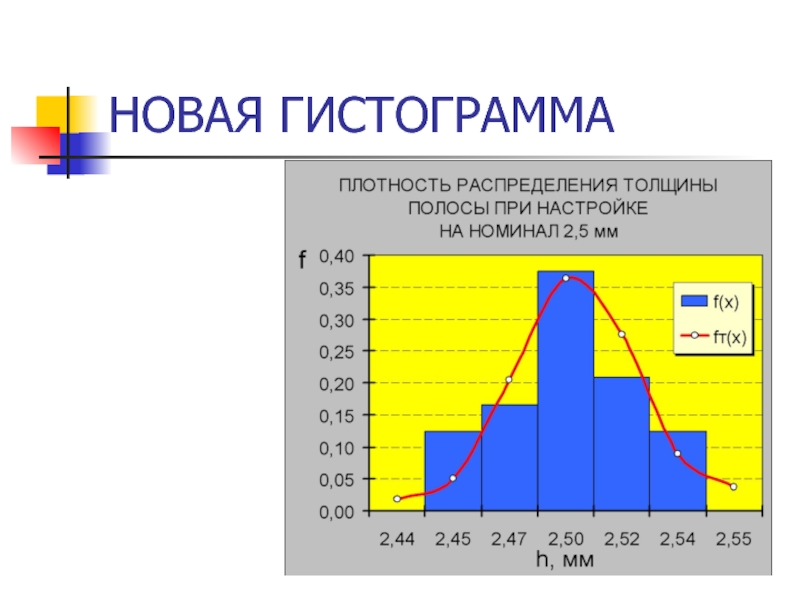
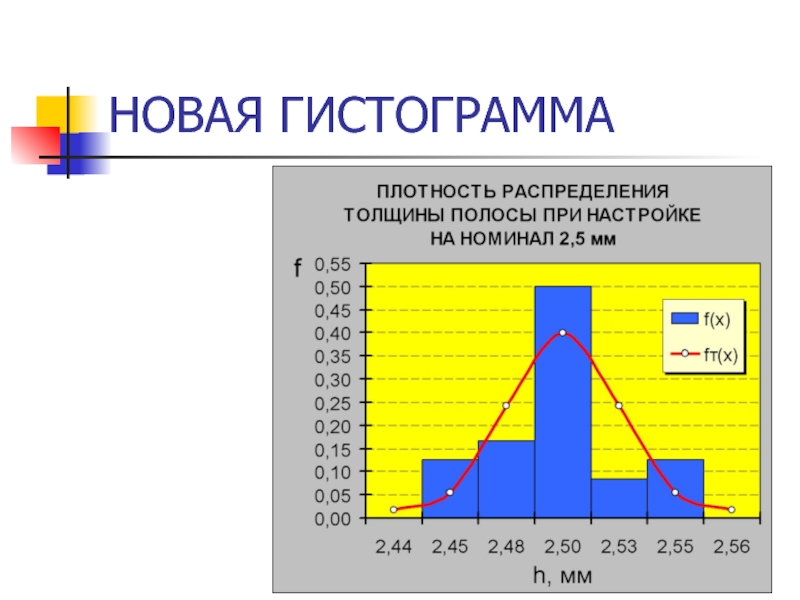
- 40. НОВАЯ ГИСТОГРАММА
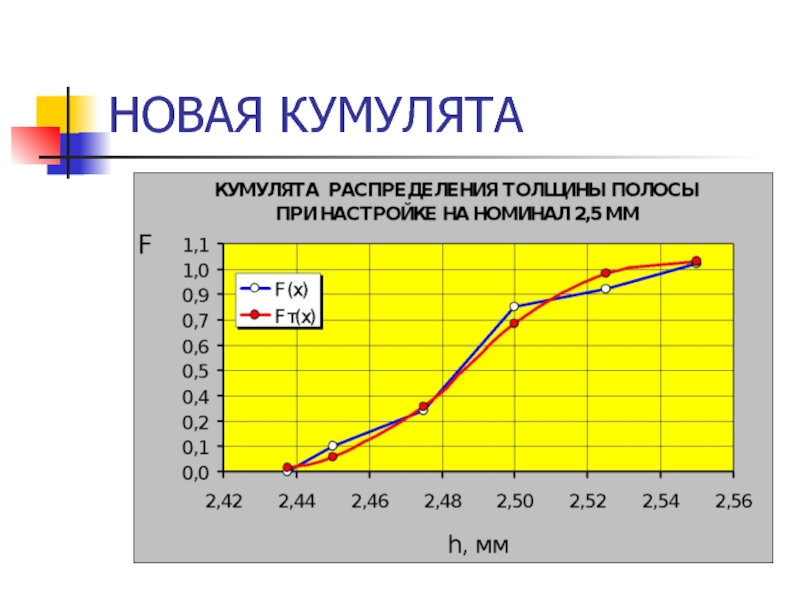
- 41. НОВАЯ КУМУЛЯТА
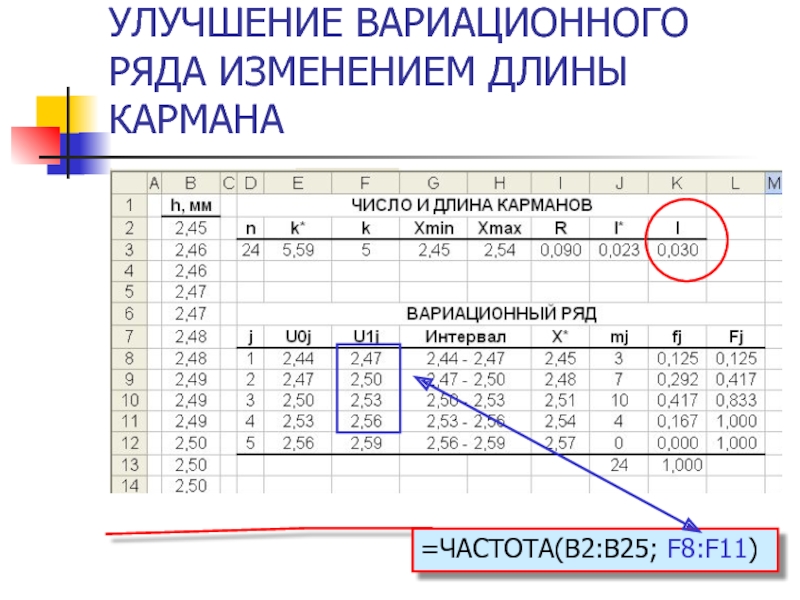
- 42. УЛУЧШЕНИЕ ВАРИАЦИОННОГО РЯДА ИЗМЕНЕНИЕМ ДЛИНЫ КАРМАНА =ЧАСТОТА(B2:B25; F8:F11)
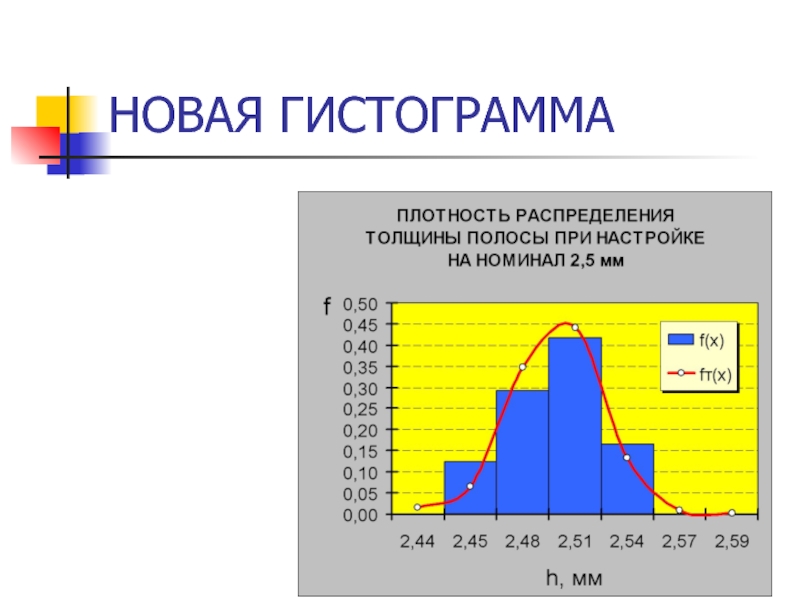
- 43. НОВАЯ ГИСТОГРАММА
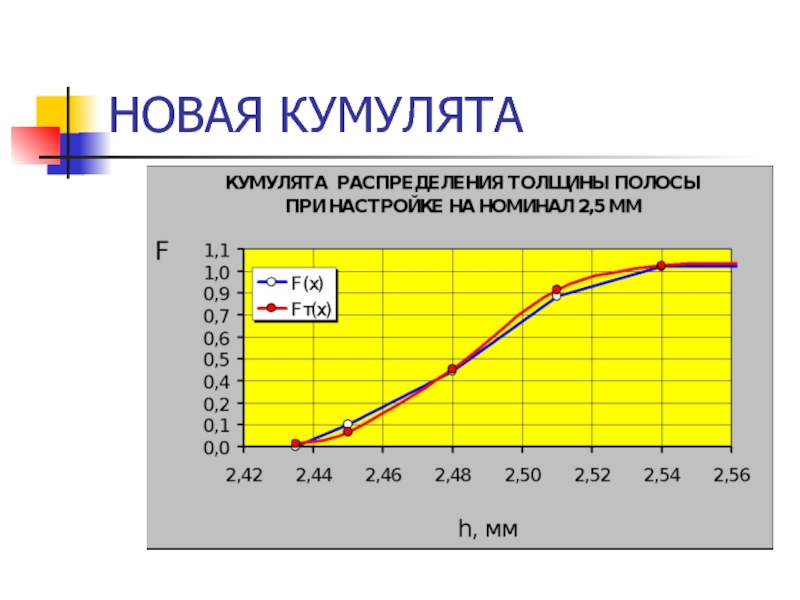
- 44. НОВАЯ КУМУЛЯТА
- 45. УЛУЧШЕНИЕ ВАРИАЦИОННОГО РЯДА ИЗМЕНЕНИЕМ ДЛИНЫ КАРМАНА =ЧАСТОТА(B2:B25; F8:F11)
- 46. НОВАЯ ГИСТОГРАММА
- 47. НОВАЯ КУМУЛЯТА
- 48. ПРИМЕНЕНИЕ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ ДЛЯ ОЦЕНКИ КАЧЕСТВА ПРОЦЕССА
- 49. СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 1) Допустимый разброс
- 50. СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 2) Наблюдается отклонение фактического
- 51. СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 3) Допустимый разброс
- 52. ПРИМЕР ИСПОЛЬЗОВАНИЯ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ ДЛЯ ОЦЕНИВАНИЯ КАЧЕСТВА ПРОЦЕССА
- 53. Распределение какого параметра было построено? Построено выборочное
- 54. ЧЕМУ РАВНЫ ДОПУСТИМЫЕ ОТКЛОНЕНИЯ АНАЛИЗИРУЕМОГО ПАРАМЕТРА? Допустимые
- 55. ЧЕМУ РАВНЫ ГРАНИЦЫ ДОПУСКА? Нижняя граница
- 56. ЧЕМУ РАВНЫ ФАКТИЧЕСКИЙ И ДОПУСТИМЫЙ РАЗБРОС?
- 57. ЧТО СЛЕДУЕТ ИЗ НАБЛЮДАЕМОГО СООТНОШЕНИЯ ФАКТИЧЕСКОГО
- 58. КАКОЙ ВЫХОД ГОДНОЙ ПРОДУКЦИИ? Так как фактический
- 59. Неободимо применить функцию распределения (кумулятивную кривую) КАК
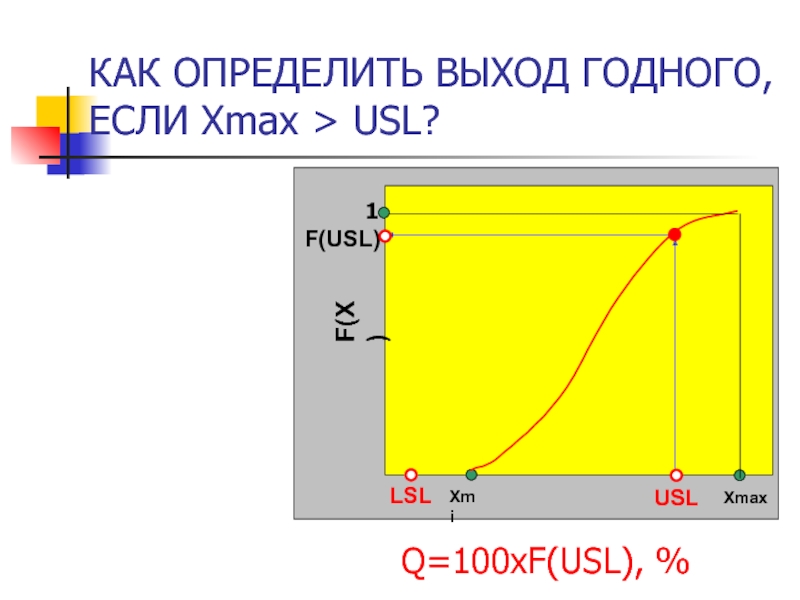
- 60. КАК ОПРЕДЕЛИТЬ ВЫХОД ГОДНОГО, ЕСЛИ Xmax >
- 61. КАК ОПРЕДЕЛИТЬ ВЫХОД ГОДНОГО, ЕСЛИ Xmin <
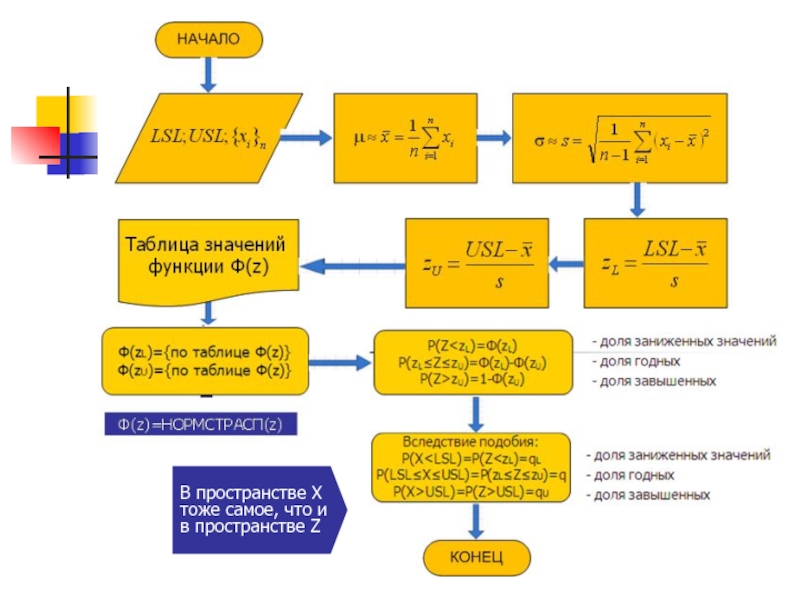
- 62. ПРИМЕНЕНИЕ СТАНДАРТНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ДЛЯ ОЦЕНКИ ОЖИДАЕМОГО
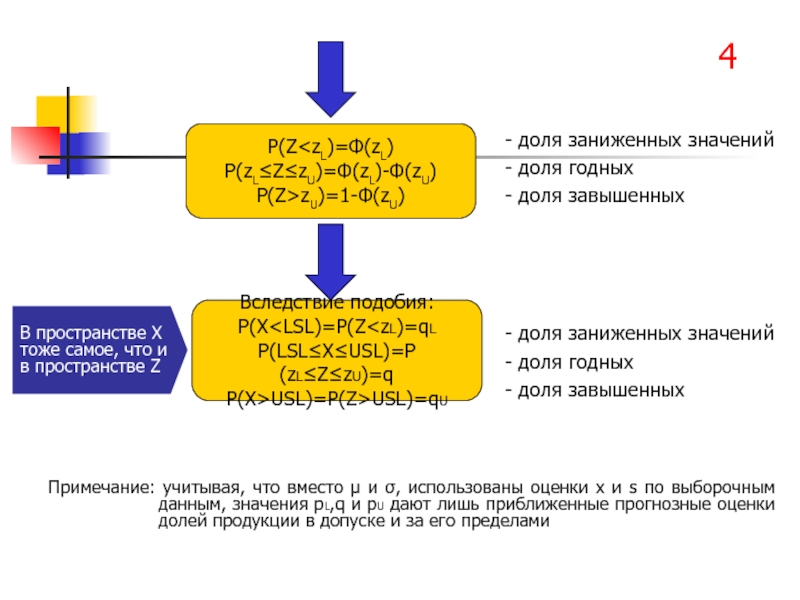
- 63. В пространстве Х тоже самое, что и в пространстве Z
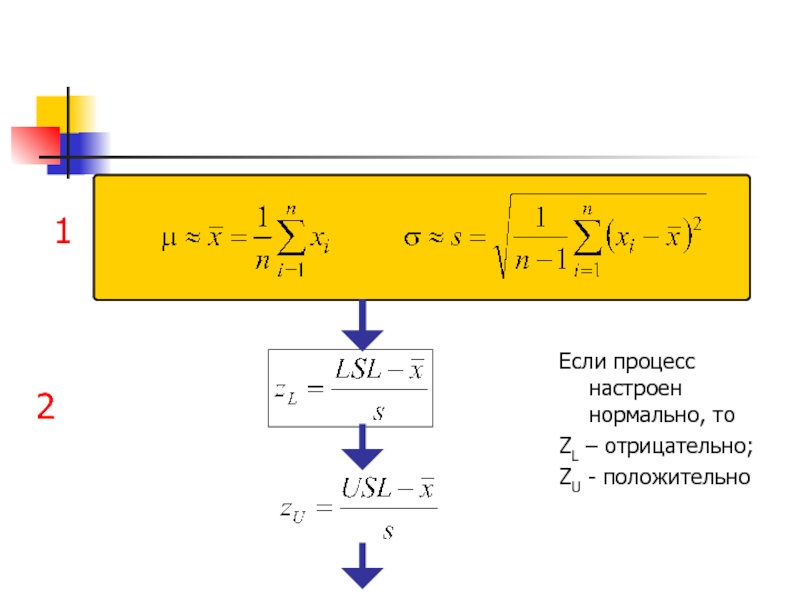
- 64. 1 2 Если процесс настроен нормально,
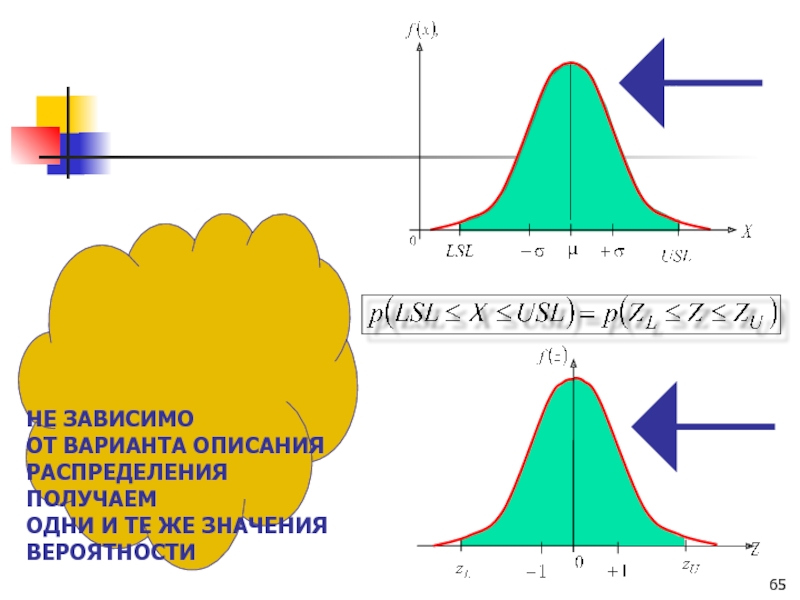
- 65. НЕ ЗАВИСИМО ОТ ВАРИАНТА
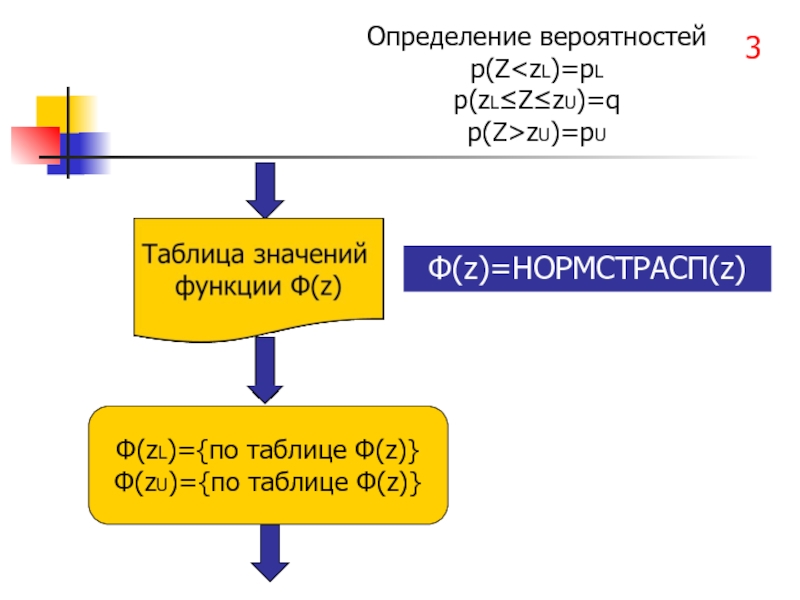
- 66. Определение вероятностей p(ZzU)=pU Ф(zL)={по таблице Ф(z)} Ф(zU)={по таблице Ф(z)} 3 Ф(z)=НОРМСТРАСП(z)
- 67. Примечание: учитывая, что вместо µ и σ,
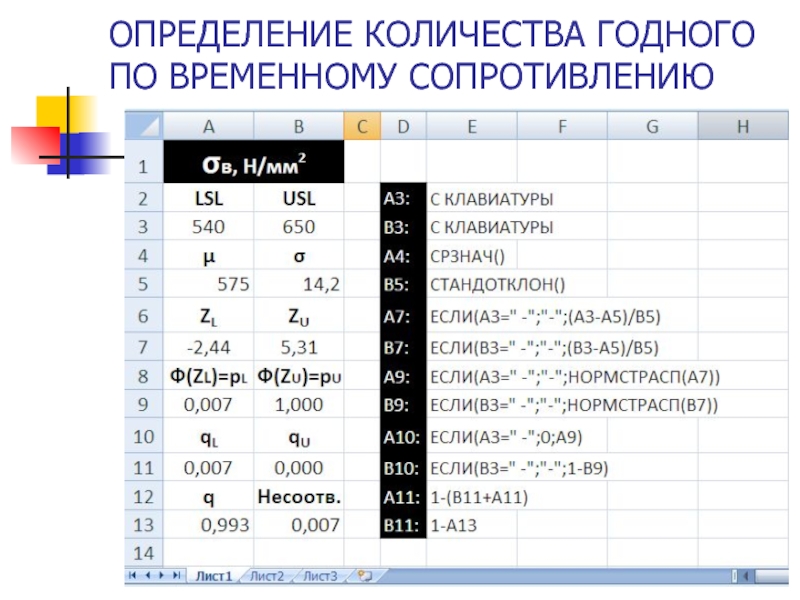
- 68. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ГОДНОГО ПО ВРЕМЕННОМУ СОПРОТИВЛЕНИЮ
- 69. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА Львовский Е.Н. Статистические методы построения
Слайд 1
СТАНДАРТИЗОВАННЫЕ МЕТОДЫ ОБРАБОТКИ
И АНАЛИЗА ЧИСЛОВОЙ ИНФОРМАЦИИ
ВЫБОРОЧНОЕ ОЦЕНИВАНИЕ
ВАРИАЦИИ ПАРАМЕТРА
Румянцев Михаил
Слайд 2
Значения параметра Х
Частота (частость) появления
Центр рассеяния
Классы значений параметра
Разброс параметра
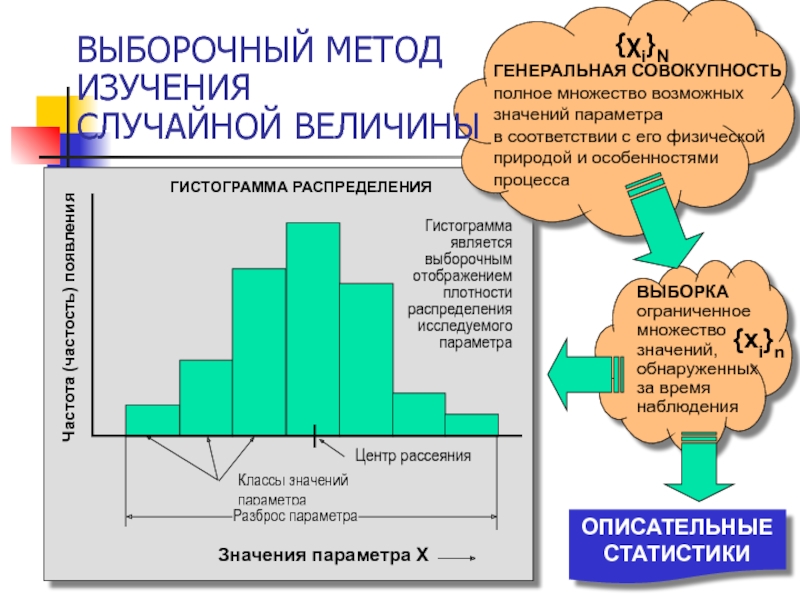
ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
полное
Гистограмма
является выборочным отображением плотности распределения исследуемого параметра
{χi}N
{xi}n
ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ
ВЫБОРОЧНЫЙ МЕТОД
ИЗУЧЕНИЯ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
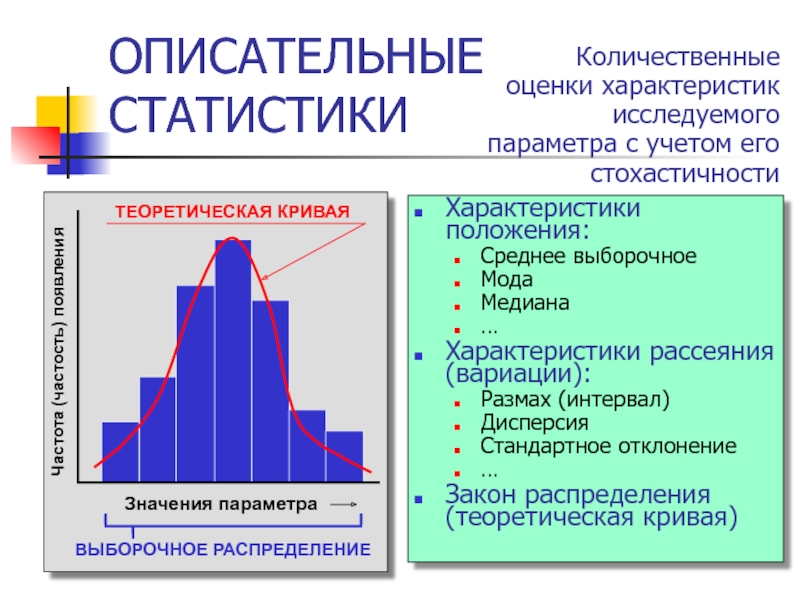
Слайд 3ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ
Характеристики положения:
Среднее выборочное
Мода
Медиана
…
Характеристики рассеяния (вариации):
Размах (интервал)
Дисперсия
Стандартное отклонение
…
Закон распределения
Количественные
оценки характеристик исследуемого параметра с учетом его стохастичности
Слайд 4ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫБОРОЧНОГО ОЦЕНИВАНИЯ
Обработка и анализ выборки.
Построение выборочного распределения
Слайд 6ЦЕЛИ ОБРАБОТКИ
И АНАЛИЗА ВЫБОРКИ
Выявление и отсеивание грубых погрешностей (проверка однородности)
Расчет
Проверка нормальности распределения
Записать уравнение теоретической кривой
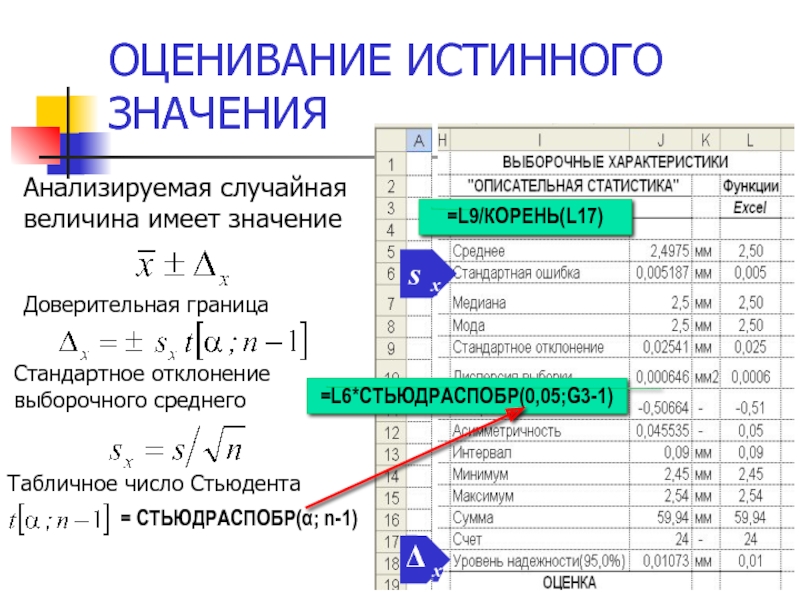
Слайд 8ОЦЕНИВАНИЕ ИСТИННОГО ЗНАЧЕНИЯ
Анализируемая случайная величина имеет значение
Доверительная граница
Стандартное
Табличное число Стьюдента
=L6*СТЬЮДРАСПОБР(0,05;G3-1)
=L9/КОРЕНЬ(L17)
Слайд 9ВЫВОД ОТНОСИТЕЛЬНО ИСТИННОГО ЗНАЧЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
С доверительной вероятностью
р=1-0,05=0,95 (т.е. 95%)
Слайд 10НЕОБХОДИМОСТЬ ПРОВЕРКИ ОДНОРОДНОСТИ
Среди элементов выборки могут оказаться результаты, содержащие грубую ошибку
Необходимо также иметь гарантию, что в полученной выборке сделана из генеральной совокупности именно того параметра, который интересует исследователя, и в ней отсутствуют элементы из какой-либо иной генеральной совокупности.
Выборку, которая содержит элементы только одной генеральной совокупности, принято называть однородной.
Слайд 12МЕТОДЫ
ОЦЕНИВАНИЯ НОРМАЛЬНОСТИ ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ
по среднему абсолютному отклонению
по размаху варьирования выборки
по
по критерию χ2
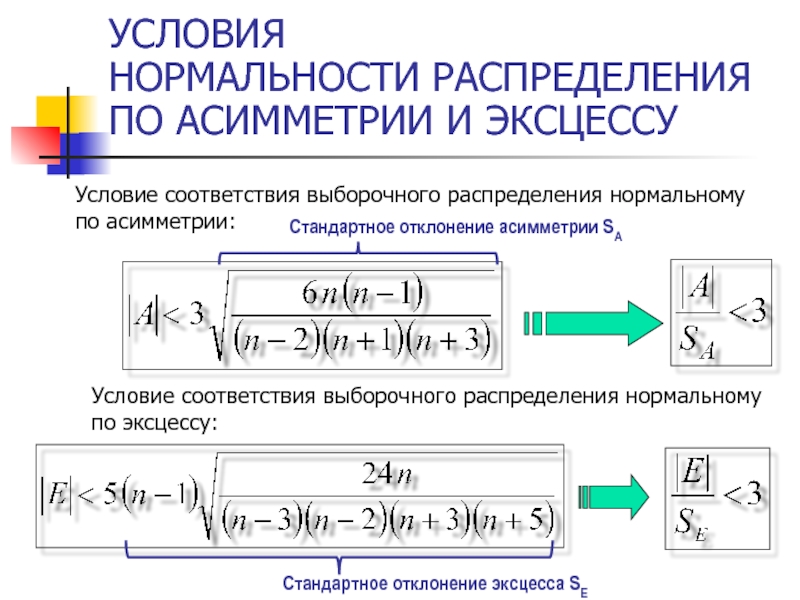
Слайд 13АСИМЕТРИЯ И ЭКСЦЕСС НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Асимметрия или коэффициент асимметрии (термин был впервые
Эксцесс (термин был впервые введен Пирсоном, 1905) или коэффициент эксцесса характеризует "пикообразность" плотности распределения. Выборочная оценка:
Для плотности нормального распределения Е = 0.
Для плотности нормального распределения А= 0.
Слайд 14УСЛОВИЯ
НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
ПО АСИММЕТРИИ И ЭКСЦЕССУ
Условие соответствия выборочного распределения нормальному по
Условие соответствия выборочного распределения нормальному по эксцессу:
Слайд 16ВЫВОДЫ ОТНОСИТЕЛЬНО ТЕОРЕТИЧЕСКОЙ КРИВОЙ
Отношение асимметрии (А=0,046) к ее стандартному отклонению (SA=0,639)
Отношение эксцесса (Е ≈ -0,507) к его стандартному отклонению (SЕ=0,918) меньше 5. Это означает, что эксцесс распределения статистически не отличается от нуля.
Таким образом, распределение анализируемого параметра можно считать нормальным.
Плотность распределения анализируемого параметра (теоретическая кривая) отображается уравнением:
Слайд 18ПОСЛЕДОВАТЕЛЬНОСТЬ ПОСТРОЕНИЯ
ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ
Построить вариационный ряд
Отобразить вариационный ряд графически в виде
Нанести на гистограмму и кумуляту теоретические кривые
Слайд 19ПОСТРОЕНИЕ ВАРИАЦИОННОГО РЯДА
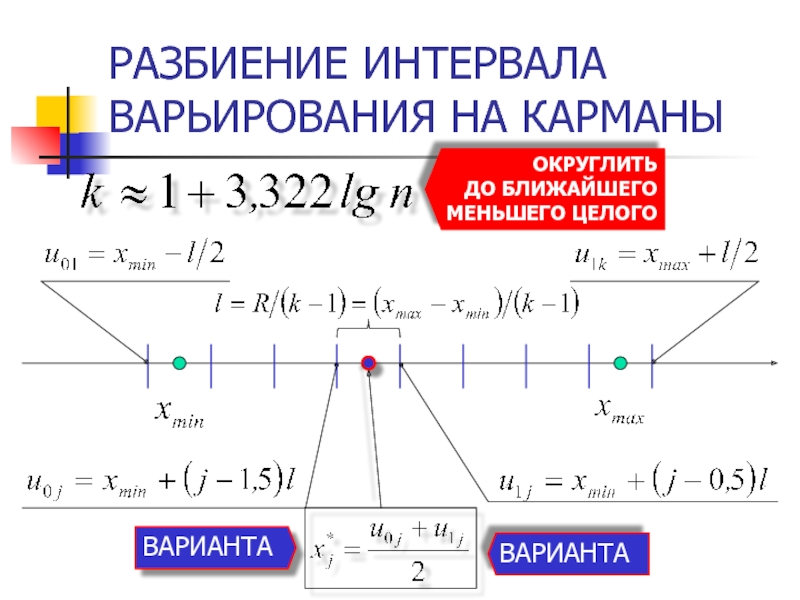
Разбить интервал варьирования параметра на классы (карманы)
Определить частоты попадания
Рассчитать дифференциальные и кумулятивные (накопленные ) частости
Слайд 20РАЗБИЕНИЕ ИНТЕРВАЛА ВАРЬИРОВАНИЯ НА КАРМАНЫ
ОКРУГЛИТЬ
ДО БЛИЖАЙШЕГО МЕНЬШЕГО ЦЕЛОГО
ВАРИАНТА
ВАРИАНТА
Слайд 23ЧАСТОТА
Число значений случайной величины, которые могут быть отнесены
к данному карману.
Возможные условия классификации значений параметра по карманам:
Сумма частот всех членов вариационного ряда равна объему исходной выборки:
Слайд 24ДИФФЕРЕНЦИАЛЬНАЯ ЧАСТОСТЬ (ЧАСТОСТЬ)
Отношение частоты некоторого члена вариационного ряда к общему количеству
Сумма частостей всех членов вариационного ряда равна единице
Слайд 25КУМУЛЯТИВНАЯ ЧАСТОСТЬ
Кумулятивная частость является выборочной оценкой
функции распределения вероятности
для значения
Для последнего кармана
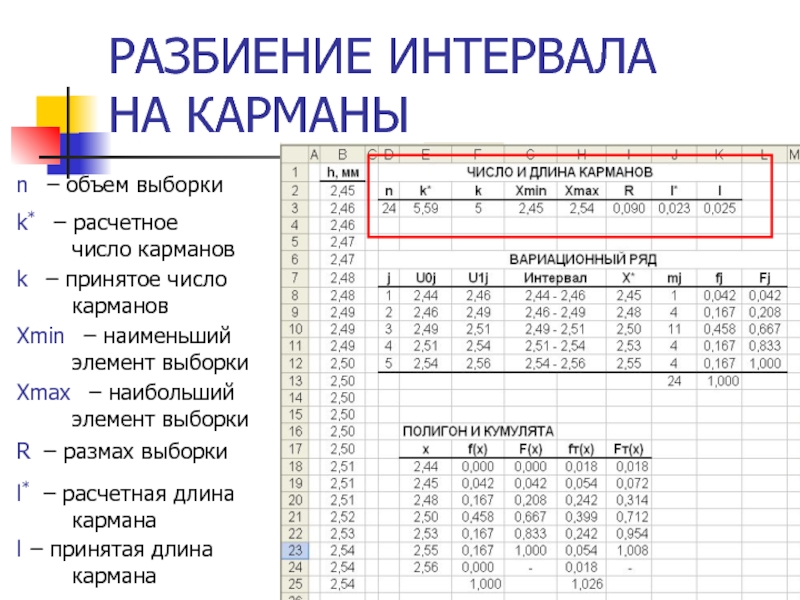
Слайд 26РАЗБИЕНИЕ ИНТЕРВАЛА
НА КАРМАНЫ
n – объем выборки
k* – расчетное
k – принятое число карманов
Xmin – наименьший элемент выборки
Xmах – наибольший элемент выборки
R – размах выборки
l* – расчетная длина кармана
l – принятая длина кармана
Слайд 27РАЗБИЕНИЕ ИНТЕРВАЛА
НА КАРМАНЫ
=МИН(B2:B25)
=МАКС(B2:B25)
=H3-G3
=I3/(F3-1)
=1+3,322*LOG10(D3)
С КЛАВИАТУРЫ
С КЛАВИАТУРЫ
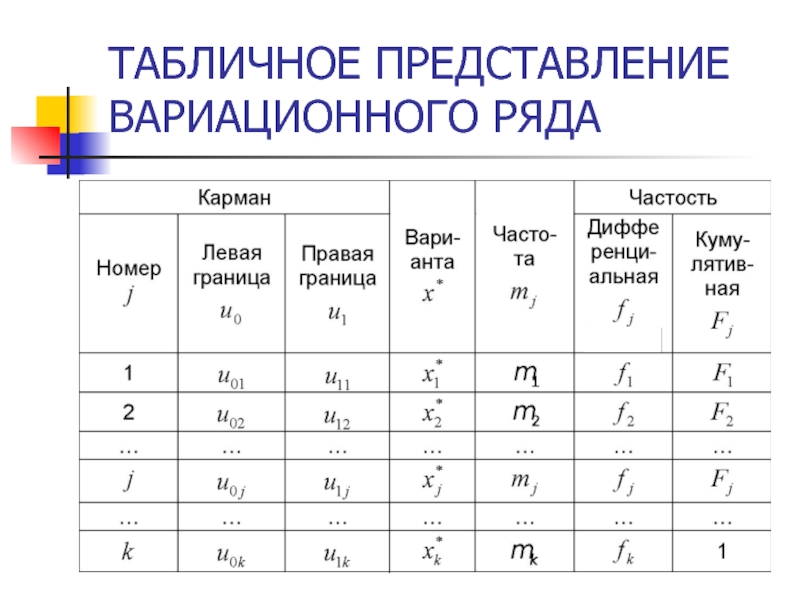
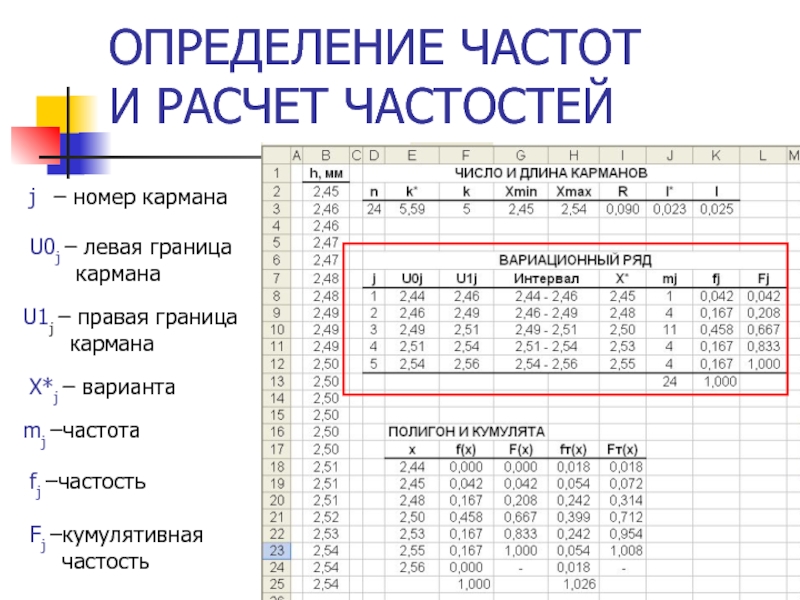
Слайд 29ОПРЕДЕЛЕНИЕ ЧАСТОТ
И РАСЧЕТ ЧАСТОСТЕЙ
U0j – левая граница кармана
U1j – правая
Х*j – варианта
mj –частота
fj –частость
Fj –кумулятивная частость
j – номер кармана
Слайд 30ОПРЕДЕЛЕНИЕ ЧАСТОТ
И РАСЧЕТ ЧАСТОСТЕЙ
=E8+$K$3
=(E8+F8)/2
=ЧАСТОТА(B2:B25;I8:I11)
=J9/$D$3
=$G$3-$K$3/2
С КЛАВИАТУРЫ
=K8
=L8+K9
Слайд 32ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ
Х – значение анализируемого параметра
f(x) – плотность распределения выборочная
F(x)
fт(x) – плотность распределения теоретическая
Fт(x) – функция распределения теоретическая
ТАБЛИЦА ДАННЫХ ДЛЯ ПОСТРОЕНИЯ ГРАФИКОВ
Слайд 33ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ
=E8
=F12
F19=K8 … F23=K12
G19=L8 … G23=L12
=(15,959*EXP(-800*(E18-2,5)^2))*$K$3
=H18
=I18+H19
Слайд 34ГРАФИЧЕСКОЕ ОТОБРАЖЕНИЕ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
Применить диаграмму типа «График-гистограмма»
Слайд 37СООТНОШЕНИЕ ПРАВОЙ ГРАНИЦЫ ПОСЛЕДНЕГО КАРМАНА И Xmax
ПРАВАЯ ГРАНИЦА ПОСЛЕДНЕГО КАРМАНА МЕНЬШЕ
ДАННЫЙ ВАРИАНТ ВАРИАЦИОННОГО РЯДА ОТОБРАЖАЕТ ЛИШЬ ЧАСТЬ ИНТЕРВАЛА ВАРЬИРОВАНИЯ АНАЛИЗИРУЕМОГО ПАРАМЕТРА.
НЕОБХОДИМО УВЕЛИЧИТЬ ДЛИНУ КАРМАНА
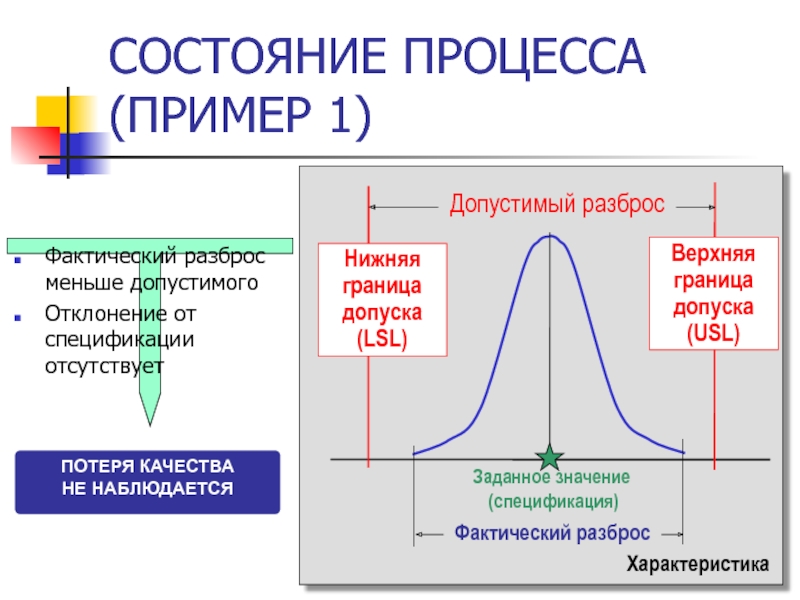
Слайд 49СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 1)
Допустимый разброс
Характеристика
Заданное значение
(спецификация)
Фактический разброс
Фактический разброс меньше допустимого
Отклонение
ПОТЕРЯ КАЧЕСТВА
НЕ НАБЛЮДАЕТСЯ
Нижняя граница допуска
(LSL)
Верхняя граница допуска
(USL)
Слайд 50СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 2)
Наблюдается отклонение фактического значения от заданного
Фактический разброс не
Допустимый разброс
Характеристика
Фактический разброс
Фактическое значение
Заданное
значение
ОТКЛОНЕНИЕ
ОТ ЗАДАННОЙ СПЕЦИФИКАЦИИ
ТЕНДЕНЦИЯ
К ПОТЕРЕ КАЧЕСТВА
LSL
USL
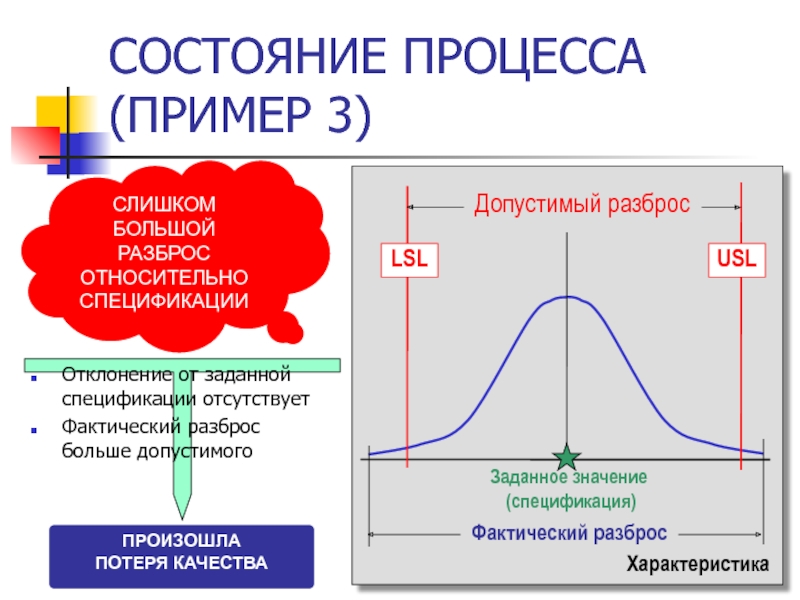
Слайд 51СОСТОЯНИЕ ПРОЦЕССА (ПРИМЕР 3)
Допустимый разброс
Характеристика
Заданное значение
(спецификация)
Фактический разброс
СЛИШКОМ БОЛЬШОЙ РАЗБРОС ОТНОСИТЕЛЬНО
Отклонение от заданной спецификации отсутствует
Фактический разброс больше допустимого
ПРОИЗОШЛА
ПОТЕРЯ КАЧЕСТВА
LSL
USL
Слайд 53Распределение какого параметра было построено?
Построено выборочное распределение толщины горячекатаной полосы шириной
Слайд 54ЧЕМУ РАВНЫ ДОПУСТИМЫЕ ОТКЛОНЕНИЯ АНАЛИЗИРУЕМОГО ПАРАМЕТРА?
Допустимые отклонения толщины горячекатаной полосы установлены
δh=±0,18 мм
Слайд 55ЧЕМУ РАВНЫ
ГРАНИЦЫ ДОПУСКА?
Нижняя граница допуска:
LSL=hном- δh=2,5-0,18=2,32 мм.
Верхняя граница допуска:
USL=hном+ δh=2,5+0,18=2,68
Слайд 56ЧЕМУ РАВНЫ ФАКТИЧЕСКИЙ
И ДОПУСТИМЫЙ РАЗБРОС?
Фактический разброс толщины
6*s=6*0,025=0,15 мм.
Допустимый разброс
Слайд 57ЧТО СЛЕДУЕТ ИЗ НАБЛЮДАЕМОГО СООТНОШЕНИЯ ФАКТИЧЕСКОГО
И ДОПУСТИМОГО РАЗБРОСА?
Так как фактический
Слайд 58КАКОЙ ВЫХОД ГОДНОЙ ПРОДУКЦИИ?
Так как фактический разброс толщины меньше допустимого, выход
Слайд 59Неободимо применить функцию распределения (кумулятивную кривую)
КАК ОПРЕДЕЛИТЬ ВЫХОД ГОДНОГО, ЕСЛИ ФАКТИЧЕСКИЙ
1
F(LSL)
USL
F(USL)
F(Х)
Q=100x[F(USL)-F(LSL)], %
Слайд 62ПРИМЕНЕНИЕ СТАНДАРТНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ДЛЯ ОЦЕНКИ ОЖИДАЕМОГО ВЫХОДА ГОДНОЙ ПРОДУКЦИИ
Имеем:
-
- Известно поле допуска с границами LSL, USL
- Получена выборка Х1, Х2,…, Хn
Требуется:
Оценить доли распределения показателя качества Х:
- за нижней границей допуска Р (Х < LSL) = qL
- в допуске Р (LSL ≤ Х ≤ USL) = q
- за верхней границей допуска Р (Х > USL) = qU
Слайд 65
НЕ ЗАВИСИМО
ОТ ВАРИАНТА ОПИСАНИЯ РАСПРЕДЕЛЕНИЯ ПОЛУЧАЕМ
ОДНИ И ТЕ ЖЕ
Нормальная
кривая
Кривая
Гаусса
Слайд 66Определение вероятностей
p(ZzU)=pU
Ф(zL)={по таблице Ф(z)}
Ф(zU)={по таблице Ф(z)}
3
Ф(z)=НОРМСТРАСП(z)
Слайд 67Примечание: учитывая, что вместо µ и σ, использованы оценки x и
- доля заниженных значений
- доля годных
- доля завышенных
Слайд 69РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Львовский Е.Н. Статистические методы построения эмпирических формул: Учебн. пособие для
Минько А.А. Статистический анализ в MS Excel. М., Изд. дом «Вильямс», 2004. 448 с.
Румянцев М.И. Обработка и анализ выборки. Магнитогорск, МГТУ, 2003.































![Неободимо применить функцию распределения (кумулятивную кривую)КАК ОПРЕДЕЛИТЬ ВЫХОД ГОДНОГО, ЕСЛИ ФАКТИЧЕСКИЙ РАЗБРОС БОЛЬШЕ ДОПУСТИМОГО? 1F(LSL)USLF(USL)F(Х)Q=100x[F(USL)-F(LSL)], %](/img/tmb/5/414484/821aed2d2afb6f9fdd4f9ed3ec05d929-800x.jpg)
![КАК ОПРЕДЕЛИТЬ ВЫХОД ГОДНОГО, ЕСЛИ Xmin < LSL? 1USLF(Х)Q=100x[1-F(LSL)], %F(LSL)](/img/tmb/5/414484/9844edeb5a2d3aed7a6e282204b06bf5-800x.jpg)