- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обернені задачі моделювання. Моделювання фізичних процесів презентация
Содержание
- 1. Обернені задачі моделювання. Моделювання фізичних процесів
- 2. кафедра медичної радіофізики Практичні задачі моделювання Є
- 3. кафедра медичної радіофізики Де таке виникає? Томографічна реконструкція Спектроскопія Надрозрізнення Непрямі вимірювання Локація …
- 4. кафедра медичної радіофізики Нехай є математична модель
- 5. кафедра медичної радіофізики Пряма задача Пряма задача
- 6. кафедра медичної радіофізики Пряма задача термодеструкції
- 7. кафедра медичної радіофізики Пряма задача переносу рентгенівського випромінювання
- 8. кафедра медичної радіофізики Не прямі задачі Обернена задача Задача синтезу Задача оптимізації
- 9. кафедра медичної радіофізики Обернена задача Знайти вхідні параметри, при яких досягаються задані вихідні значення
- 10. кафедра медичної радіофізики Обернена задача Знайти функцію
- 11. кафедра медичної радіофізики Задача синтезу Знайти модель,
- 12. кафедра медичної радіофізики Задача синтезу для переносу
- 13. кафедра медичної радіофізики Задача синтезу для ЯМР
- 14. кафедра медичної радіофізики Задача оптимізації Знайти всі параметри, при яких заданий цільовий функціонал має екстремум
- 15. кафедра медичної радіофізики Оптимізація При яких параметрах
- 16. кафедра медичної радіофізики Особливості не прямих задач
- 17. кафедра медичної радіофізики Цікавий факт Прямі задачі
- 18. кафедра медичної радіофізики Приклади нестійких задач Часто
- 19. кафедра медичної радіофізики Задача спектроскопії
- 20. кафедра медичної радіофізики Чому ця задача нестійка?
- 21. кафедра медичної радіофізики Які ще задачі нестійкі?
- 22. кафедра медичної радіофізики Коректно та некоректно поставлені
- 23. кафедра медичної радіофізики Страшна проблема Питання: що
- 24. кафедра медичної радіофізики Розв’язання некоректних задач Звести
- 25. кафедра медичної радіофізики Співставлення за точністю
- 26. кафедра медичної радіофізики Деякі методи для задач
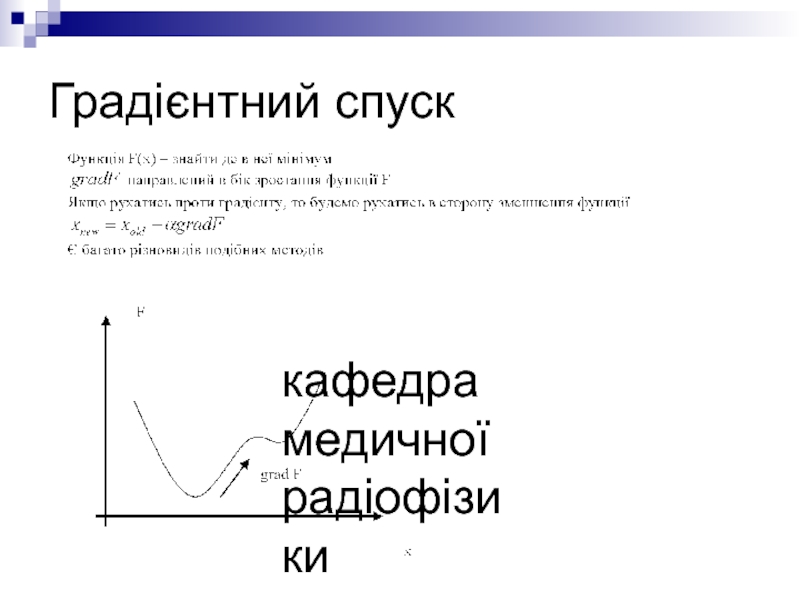
- 27. кафедра медичної радіофізики Градієнтний спуск
- 28. кафедра медичної радіофізики Деякі методи для зворотних
- 29. кафедра медичної радіофізики Регуляризація за Тихоновим Теорема
- 30. кафедра медичної радіофізики Регуляризація за Тихоновим Задача
- 31. кафедра медичної радіофізики Приклади регуляризації за Тихоновим
- 32. кафедра медичної радіофізики Метод підбору
- 33. кафедра медичної радіофізики Метод псевдорозв’язку
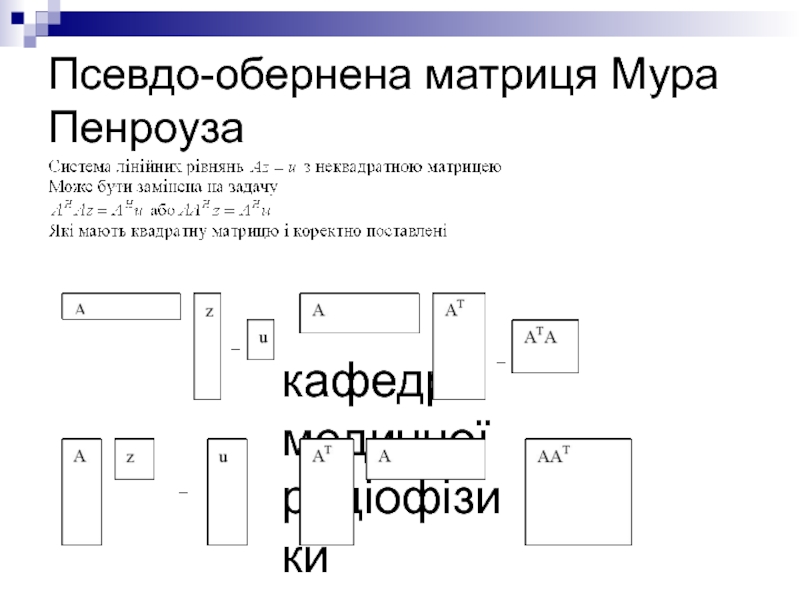
- 34. кафедра медичної радіофізики Псевдо-обернена матриця Мура Пенроуза
- 35. кафедра медичної радіофізики Метод заміни рівняння близьким до нього
- 36. кафедра медичної радіофізики Метод урізаного сингулярного розвинення
- 37. кафедра медичної радіофізики Метод Лагранжа Задача замінюється варіаційної
- 38. кафедра медичної радіофізики Нормальний розв’язок системи лінійних рівнянь
- 39. кафедра медичної радіофізики Метод ітерацій
- 40. кафедра медичної радіофізики Метод параметричної регресії Створюється
- 41. кафедра медичної радіофізики Задача При томографії твердого
- 42. кафедра медичної радіофізики Реконструкція спінової густини і
- 43. кафедра медичної радіофізики Дискретизація задачі Час і
- 44. кафедра медичної радіофізики Розв’язок Рівняння замінюємо варіаційною
- 45. кафедра медичної радіофізики Метод Проні Прямий розв’язок
- 46. кафедра медичної радіофізики Метод Проні
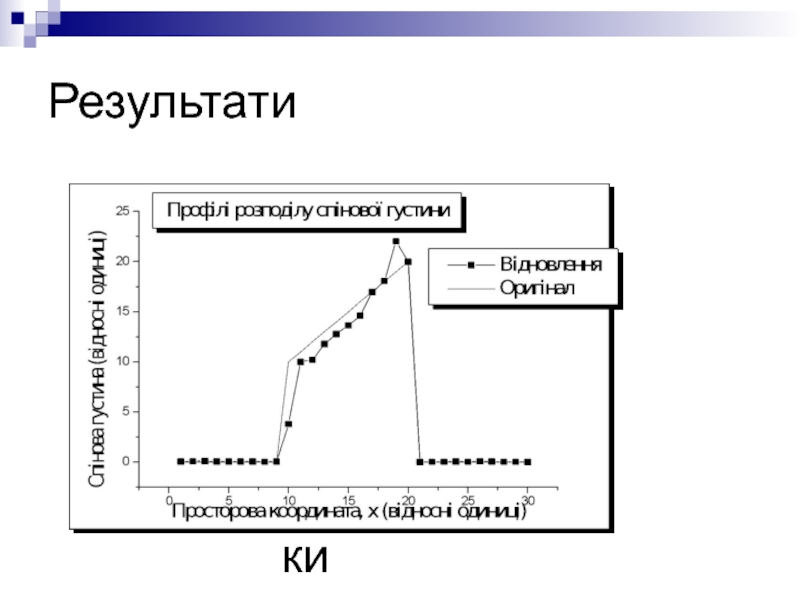
- 47. кафедра медичної радіофізики Результати
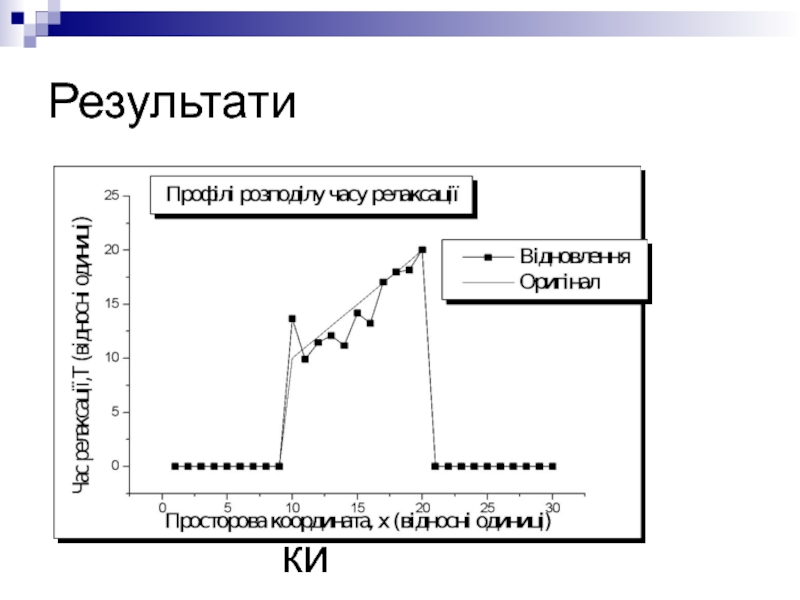
- 48. кафедра медичної радіофізики Результати
- 49. кафедра медичної радіофізики Висновки Зворотні задачі та
- 50. кафедра медичної радіофізики Питання
Слайд 1кафедра медичної радіофізики
Обернені задачі моделювання
“Моделювання фізичних процесів ”Лекція 2
Судаков О.О.
Слайд 2кафедра медичної радіофізики
Практичні задачі моделювання
Є модель, є вхідні дані, є вихідні
Ми розглядали: як при заданих вхідних даних знайти вихідні дані на основі моделі
На практиці частіше цікавить інше:
при яких вхідних даних та заданій моделі отримаємо задані вихідні дані?
Яка модель, що відповідає заданим вхідним та вихідним даним?
При яких параметрах задачі досягається найкращий результат і що це за результат?
Слайд 3кафедра медичної радіофізики
Де таке виникає?
Томографічна реконструкція
Спектроскопія
Надрозрізнення
Непрямі вимірювання
Локація
…
Слайд 5кафедра медичної радіофізики
Пряма задача
Пряма задача моделювання – знайти значення характеристики при
Слайд 9кафедра медичної радіофізики
Обернена задача
Знайти вхідні параметри, при яких досягаються задані вихідні
Слайд 10кафедра медичної радіофізики
Обернена задача
Знайти функцію джерела термодетрукції, яка задає заданий розподіл
Знайти значення параметрів речовини, що відповідають заданому розподілу інтенсивності – задача томографічної реконструкції
Слайд 11кафедра медичної радіофізики
Задача синтезу
Знайти модель, яка для заданих вхідних значень дає
Слайд 12кафедра медичної радіофізики
Задача синтезу для переносу рентгенівського випромінювання
Знайти яка повинна бути
Слайд 13кафедра медичної радіофізики
Задача синтезу для ЯМР томографії
Знайти розподіл магнітного поля (імпульсну
Слайд 14кафедра медичної радіофізики
Задача оптимізації
Знайти всі параметри, при яких заданий цільовий функціонал
Слайд 15кафедра медичної радіофізики
Оптимізація
При яких параметрах задачі, що реалізуються на практиці, розподіл
При яких умовах, що практично реалізуються, доза не виходить за допустимі межі і досягається найкращий ефект
Слайд 16кафедра медичної радіофізики
Особливості не прямих задач
Може не існувати розв’язку
Може існувати багато
Розв’язок (розв’язки) бути не стійкі, або не відповідати здоровому глузду
Слайд 17кафедра медичної радіофізики
Цікавий факт
Прямі задачі та задачі оптимізації найчастіше розв’язуються так,
Обернені та задачі синтезу частіше не розв’язуються так, як хотілось
Слайд 18кафедра медичної радіофізики
Приклади нестійких задач
Часто задача має розв’язок, але нестійка до
Задача спектроскопії
Задача проективної томографії
Розв’язання погано обумовлених та великих систем лінійних рівнянь
Слайд 21кафедра медичної радіофізики
Які ще задачі нестійкі?
Інтегральні рівняння першого роду
Системи лінійних рівнянь
Числове диференціювання
Слайд 22кафедра медичної радіофізики
Коректно та некоректно поставлені задачі
Задача називається коректно поставленою (за
Задача має розв’язок
Розв’язок єдиний
Задача стійка за вхідними параметрами
Всі інші задачі – некоректно поставлені
Слайд 23кафедра медичної радіофізики
Страшна проблема
Питання: що робити, якщо виникла некоректна задача, яка
Не має розв’язку
Має багато розв’язків
Розв’язок не стійкий, або не має смислу
Відповідь: брати і все одно розв’язувати задачу
Слайд 24кафедра медичної радіофізики
Розв’язання некоректних задач
Звести задачу до коректно поставленої, розв’язок якої
Часто дуже важка проблема: не скільки наука, скільки мистецтво
Слайд 25кафедра медичної радіофізики
Співставлення за точністю
Зміна задачі змінює розв’язок
Реальні вхідні дані
Співставлення за точністю
Слайд 26кафедра медичної радіофізики
Деякі методи для задач оптимізації (коректних)
Зворотне керування
Лінійне та нелінійне
Методи градієнтного спуску
Слайд 28кафедра медичної радіофізики
Деякі методи для зворотних задач, задач синтезу та інших
Розв’язання прямої задачі шляхом підбору параметрів
Регуляризація за Тихоновим
Параметрична регресія
Штучні нейронні мережі
Слайд 29кафедра медичної радіофізики
Регуляризація за Тихоновим
Теорема Тихонова
Якщо розв’язок заданий на компакті (обмежена,
Слайд 30кафедра медичної радіофізики
Регуляризація за Тихоновим
Задача змінюється так, щоб розв’язок був заданий
Штучні обмеження на розв’зок:
Неперервний
Обмежений
Мінімальна енергія
Обмежений спектр
Обмежена похідна
Слайд 31кафедра медичної радіофізики
Приклади регуляризації за Тихоновим
Метод підбору
Метод квазі (псевдо) розв’язку
Псевдо-обернена матриця
Метод заміни рівняння близьким до нього
Метод урізаного сингулярного розвинення
Метод знаходження регуляризуючого оператора
Метод Лагранжа
Метод ітерацій
Слайд 36кафедра медичної радіофізики
Метод урізаного сингулярного розвинення (метод головних компонент)
Потужний метод для
Слайд 40кафедра медичної радіофізики
Метод параметричної регресії
Створюється проста модель з невідомими параметрами
Параметри підбираються
Підходить як для зворотних задач так і для задач синтезу
Слайд 41кафедра медичної радіофізики
Задача
При томографії твердого тіла час поперечної релаксації дуже малий
Чи
Чи можна за одним сигналом відновити як час поперечної релаксаціі так і спінову густину?
Слайд 42кафедра медичної радіофізики
Реконструкція спінової густини і часу поперечної релаксації за сигналом
Є сигнал томографа. Чи можна за одним сигналом відновити як час поперечної релаксаціі так і спінову густину?
Слайд 43кафедра медичної радіофізики
Дискретизація задачі
Час і просторові координати замінюємо дискретним набором параметрів
За
Слайд 44кафедра медичної радіофізики
Розв’язок
Рівняння замінюємо варіаційною задачею на екстремум
Знайти ρ та z
Для достовірного розв’язку треба, щоб кількість вхідних відліків була більше, або рівна кількості параметрів
Слайд 45кафедра медичної радіофізики
Метод Проні
Прямий розв’язок варіаційної задачі складний, оскільки рівняння нелінійні
Треба
Метод Проні (1796 р)
Слайд 49кафедра медичної радіофізики
Висновки
Зворотні задачі та задачі синтезу – некоректні
Для розв’язку таких
Розв’язок некоректної задачі може бути дуже наближеним
Отримання хороших результатів – не скільки наука, скільки мистецтво