- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Зв’язаність графів. Шляхи, цикли ізоморфізм презентация
Содержание
- 1. Зв’язаність графів. Шляхи, цикли ізоморфізм
- 2. Зміст Вступ…………………………………………………. 3 Шлях…………………….………………………….. 4 Цикл.................................... …………………………..6 Теорема............................................................... ……..7 Орієнтований граф …………………………………..8
- 3. Вступ Теорія графів — одна з істотних
- 4. Шлях Шляхом довжиною r [52] із вершини
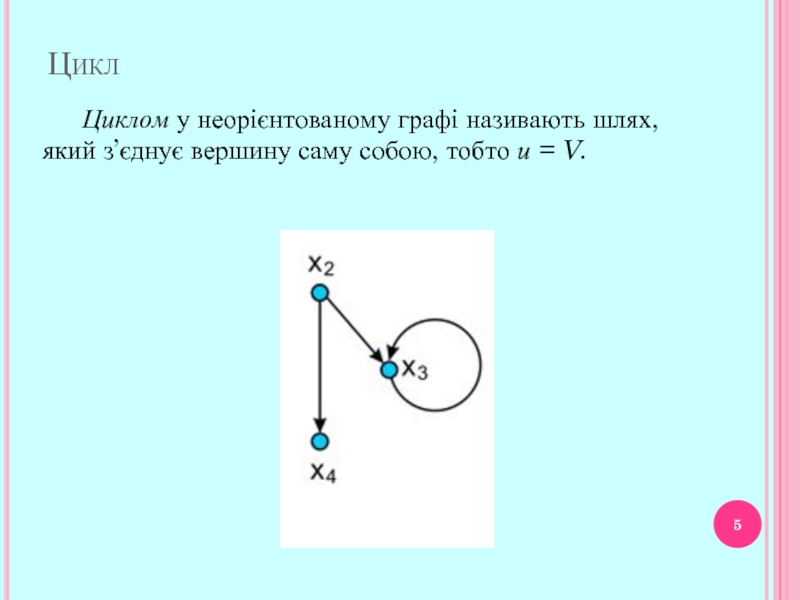
- 5. Циклом у неорієнтованому графі називають шлях,
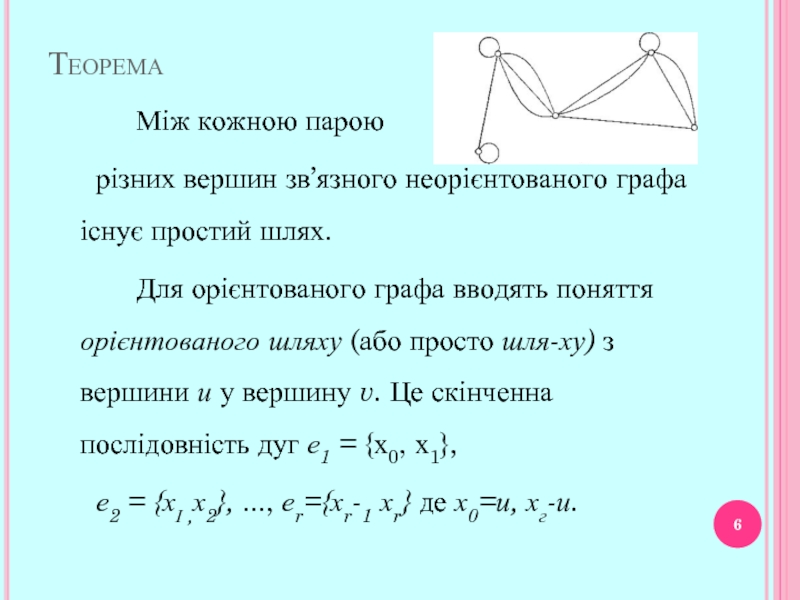
- 6. Теорема Між кожною парою
- 7. Орієнтований
- 8. Зв’язаність графів
- 9. Ізоморфізм графів
- 10. Нехай
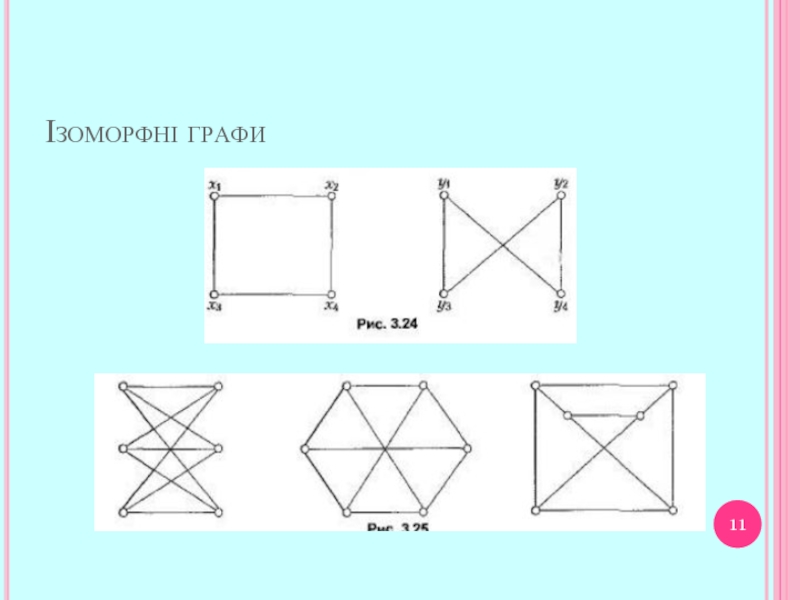
- 11. Ізоморфні графи
- 12. Теорема
- 13. Проблема визначення
- 14. Висновки Отже, не існує набору інваріантів для
- 15. Список літератури 1. Нікольський Ю. В. Дискретна
Слайд 2Зміст
Вступ…………………………………………………. 3
Шлях…………………….………………………….. 4
Цикл.................................... …………………………..6
Теорема............................................................... ……..7
Орієнтований граф …………………………………..8
Зв’язаність графів................................ ……………….9
Ізоморфізм графів................................................... …10
Ізоморфні графи.........……………………...……..11
Теорема............... ……………………………………12
Проблеми визначення……….……………………...13
Висновки …………………………………………....14
Список літератури ……………………………….....15
Слайд 3Вступ
Теорія графів — одна з істотних частин математичного апарату інформатики та
кібернетики. У термінах теорії графів можна сформулювати багато задач, пов’язаних із дискретними об’єктами. Такі задачі виникають у проектуванні інтегральних схем і схем управління, у дослідженні автоматів, в економіці й статистиці, теорії розкладів і дискретній оптимізації.
Слайд 4Шлях
Шляхом довжиною r [52] із вершини и в вершину v в
неорієнтованому графі називають послідовність ребер е1 = {х0, х1}, е2 = {хІ ,х2}, ..., еr={хr-1 хr} де хr = v, r — натуральне число. Отже, шлях довжиною r має r ребер, причому ребро враховують стільки разів, скільки воно міститься в шляху. Вершини v та e називають крайніми, а решту вершин шляху — внутрішніми.
Слайд 5
Циклом у неорієнтованому графі називають шлях, який з’єднує вершину саму собою,
тобто и = V.
Цикл
Слайд 6
Теорема
Між кожною парою
різних вершин зв’язного неорієнтованого графа існує простий шлях.
Для
орієнтованого графа вводять поняття орієнтованого шляху (або просто шляху) з вершини и у вершину v. Це скінченна послідовність дуг е1 = {х0, х1},
е2 = {хІ ,х2}, ..., еr={хr-1 хr} де х0=и, хг-и.
е2 = {хІ ,х2}, ..., еr={хr-1 хr} де х0=и, хг-и.
Слайд 7
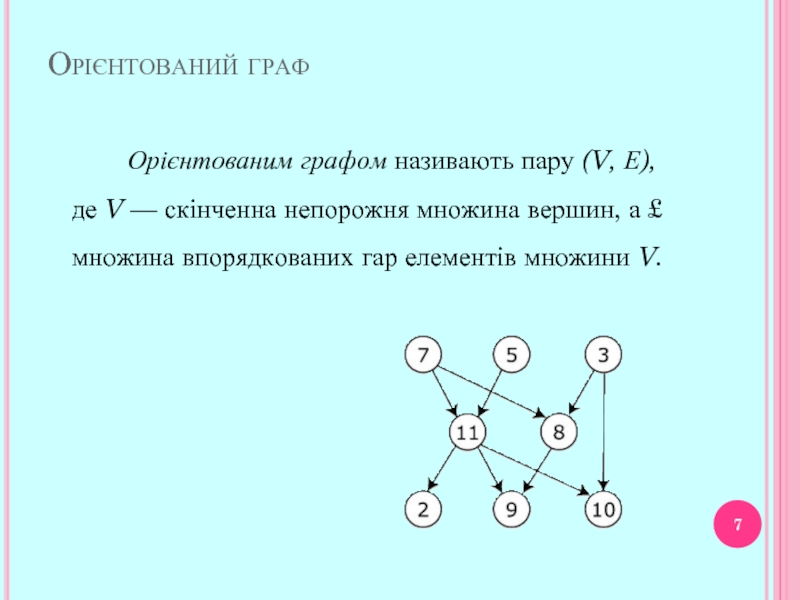
Орієнтований граф
Орієнтованим графом називають пару (V, Е), де
V — скінченна непорожня множина вершин, а £ множина впорядкованих гар елементів множини V.
Слайд 8Зв’язаність графів
Орієнтований граф називають сильно зв’язним, якщо для
будь-яких його різних вершин и та V існують орієнтовані шляхи від и до V та від її до и. Позначають так: A=B
Орієнтований граф називають слабко зв’язним, якшо існує шлях між будь-якими двома різними вершинами у відповідному йому неорієнтованому графі (тобто без урахування напрямку дуг).
Орієнтований граф називають слабко зв’язним, якшо існує шлях між будь-якими двома різними вершинами у відповідному йому неорієнтованому графі (тобто без урахування напрямку дуг).
Слайд 9Ізоморфізм графів
У теорії графів і її застосуваннях істотно,
що існують об’єкти (вершини графа) і зв’язки між ними (ребра). Тому доцільно не розрізняти графи, котрі можна одержати один з одного зміною позначень вершин. Сформулюємо ці міркування у вигляді наступного означення.
Слайд 10
Нехай G1 = (VІ, Е1) і G2=(V2, Е2)
прості графи, а φ: Vх → V2 — бієкція. Якщо для будь-яких вершин u та v графа G1 їх образи φ(u) та φ(v) суміжні в G2 тоді й лише тоді, коли и та v суміжні в G1 то цю бієкцію називають ізоморфізмом графа G1 на граф G2, а графи G1 G2 — ізоморфними.
Отже,
V и, v ≡ v1 ({и, v} ≡ Е1 тоді й лише тоді, коли {φ(u), φ(v)} ≡ Е2)
Отже,
V и, v ≡ v1 ({и, v} ≡ Е1 тоді й лише тоді, коли {φ(u), φ(v)} ≡ Е2)
Слайд 12Теорема
Прості графи ізоморфні тоді й лише тоді, коли
їх матриці суміжності можна отримати одну з одної однаковими перестановками рядків і стовпців.
Виявити ізоморфізм дуже складно. Теоретично алгоритм перевірки пари простих графів на ізоморфізм існує, але він не зручний.
Виявити ізоморфізм дуже складно. Теоретично алгоритм перевірки пари простих графів на ізоморфізм існує, але він не зручний.
Слайд 13Проблема визначення
Часто неважко довести, що два прості графи
не ізоморфні, якщо порушується ачастивість, інваріантна щодо ізоморфізму, наприклад:
кількість вершин;
кількість ребер;
кількість вершин конкретного степеня (вершині
v ≡ V1, deg(v) = d, має відпо відати вершина
u = φ(v) ≡ V2, deg(u) = d.
Є й інші інваріанти, але порушення інваріантності — це лише достатня умовг неізоморфності графів.
кількість вершин;
кількість ребер;
кількість вершин конкретного степеня (вершині
v ≡ V1, deg(v) = d, має відпо відати вершина
u = φ(v) ≡ V2, deg(u) = d.
Є й інші інваріанти, але порушення інваріантності — це лише достатня умовг неізоморфності графів.
Слайд 14Висновки
Отже, не існує набору інваріантів для виявлення ізоморфізму.
Для сильної зв’язності орієнтованого
графа має існувати послідовність дуг з урахуванням орієнтації від будь-якої вершини графа до будь-якої іншої.
Шлях, буквально, - це послідовність ребер
Між кожною парою різних вершин зв’язного неорієнтованого графа існує простий шлях.
Шлях, буквально, - це послідовність ребер
Між кожною парою різних вершин зв’язного неорієнтованого графа існує простий шлях.
Слайд 15Список літератури
1. Нікольський Ю. В. Дискретна математика/ Ю. В. Нікольський, В.
В. Пасічник, Ю. М. Щербина. – Київ: Видавнича група BHV, 2007. – 367 с.



![Шлях Шляхом довжиною r [52] із вершини и в вершину v в неорієнтованому графі називають послідовність](/img/tmb/3/225310/e5790c684eba18f7b929b4e581670e11-800x.jpg)