- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Зеркальная симметрия презентация
Содержание
- 1. Зеркальная симметрия
- 2. Определение Зеркальная симметрия. Это симметрия в
- 3. Виды симметрии: а) Лучевая симметрия б) Осевая симметрия в) Центральная симметрия г) Зеркальная симметрия
- 4. Фигуры, симметричные относительно плоскости Фигуры, симметричные
- 5. Это математическое понятие описывает соотношение в
- 6. Геометрическая фигура называется симметричной относительно плоскости S , если для
- 7. Система в пирамиде Симметрия в пирамиде
- 8. Симметрия правильной пирамиды Ось симметри: при четном
- 9. Термин зеркальная симметрия употребляется также для
- 10. Источники: http://dic.academic.ru https://ru.wikipedia.org/wiki/Заглавная_страница http://works.doklad.ru/view/l2RHBdcyf0k/2.html
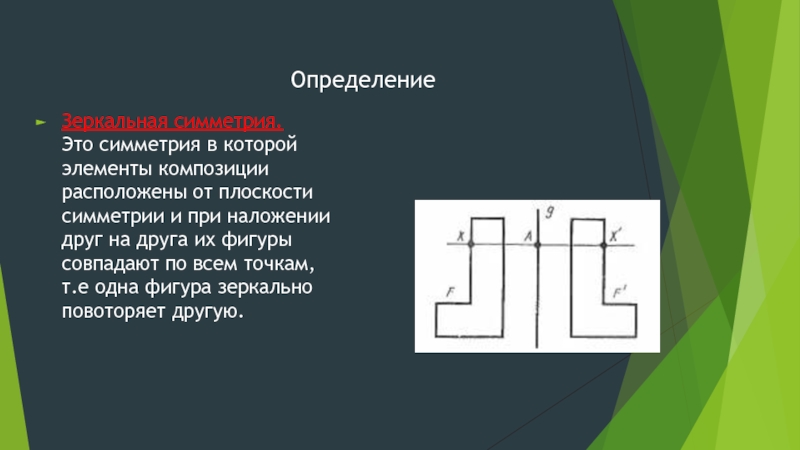
Слайд 2Определение
Зеркальная симметрия.
Это симметрия в которой
элементы композиции
расположены от плоскости
симметрии и при
наложении
друг на друга их фигуры
совпадают по всем точкам,
т.е одна фигура зеркально
повоторяет другую.
Слайд 3
Виды симметрии:
а) Лучевая симметрия
б) Осевая симметрия
в) Центральная симметрия
г) Зеркальная симметрия
Слайд 4Фигуры, симметричные относительно плоскости
Фигуры, симметричные относительно плоскости. Фигура ( тело) называется
симметричной относительно некоторой плоскости, если эта плоскость разбивает фигуру на две равные симметричные части.
Слайд 5
Это математическое понятие описывает соотношение в оптике объектов и их (мнимых)
изображений при отражении в плоском зеркале, а также многие законы симметрии.
Слайд 6
Геометрическая фигура называется симметричной относительно плоскости S , если для каждой точки E этой фигуры может быть найдена
точка E1 этой же фигуры, так что отрезок EE1 перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE1 ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова. Они называются зеркально равными.
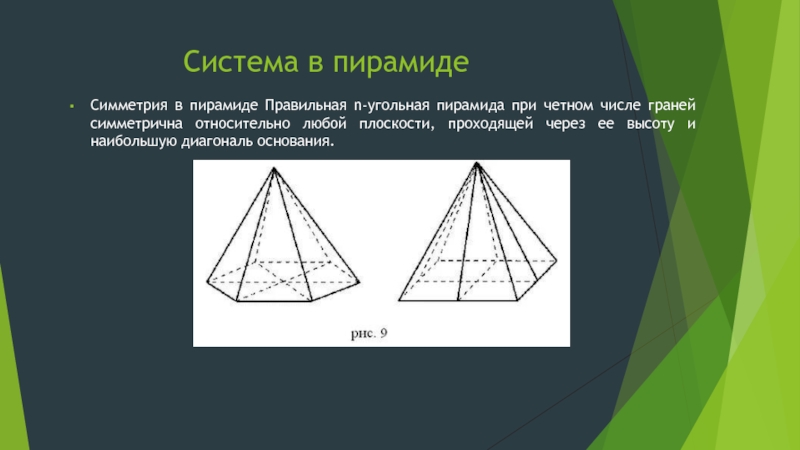
Слайд 7Система в пирамиде
Симметрия в пирамиде Правильная n-угольная пирамида при четном числе
граней симметрична относительно любой плоскости, проходящей через ее высоту и наибольшую диагональ основания.
Слайд 8Симметрия правильной пирамиды
Ось симметри: при четном числе сторон основания- ось симметрии,
проходящая через вершину правильной пирамиды и цент основания.
Слайд 9
Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта,
то есть, когда объект при операции отражения переходят в себя. Это математическое понятие описывает соотношение в объектов и их изображений при отражении в плоском зеркале, а также многие законы симметрии (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении)