- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
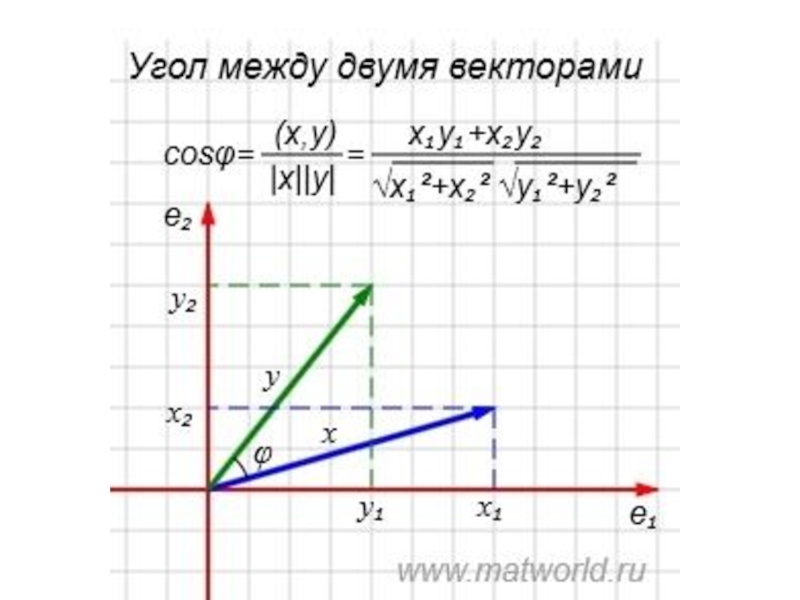
Задачи в координатах II презентация
Содержание
Содержание Радиус-вектор Связь между координатами вектора и координатами его начала и конца Координаты середины отрезка Вычисление длины вектора по его координатам Расстояние между двумя точками
Слайд 2Содержание
Радиус-вектор
Связь между координатами вектора и координатами его начала и конца
Координаты середины отрезка
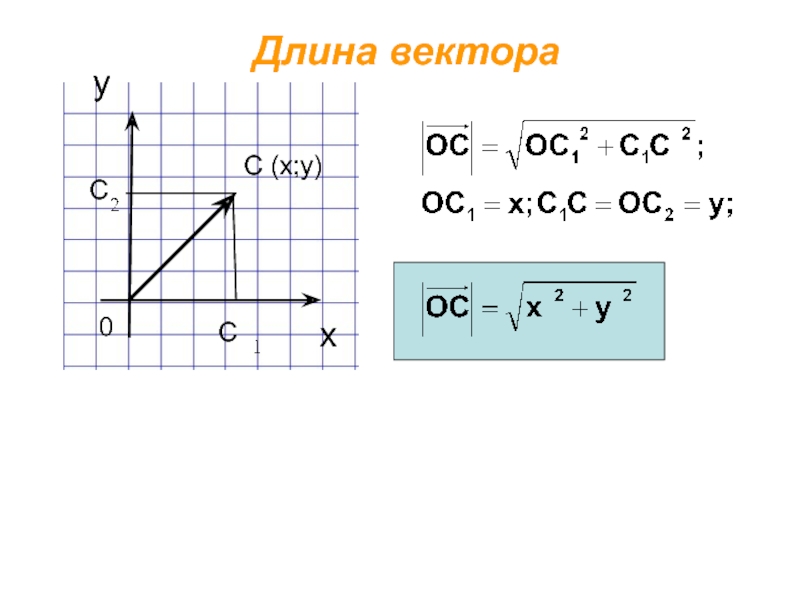
Вычисление длины вектора по его координатам
Расстояние между двумя точками
Слайд 3
х
у
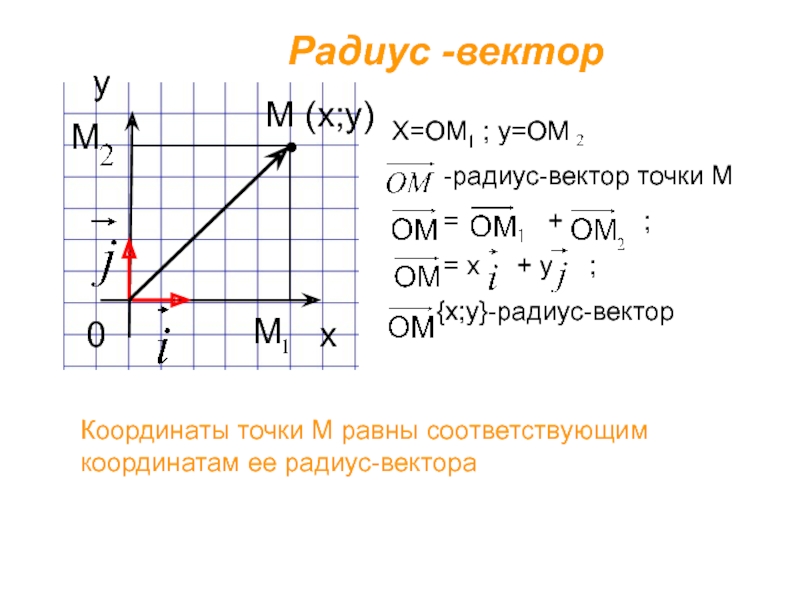
Радиус -вектор
М (х;у)
0
М
М
Х=ОМ ; у=ОМ
-радиус-вектор точки М
= + ;
= х + у ;
{х;у}-радиус-вектор
= + ;
= х + у ;
{х;у}-радиус-вектор
Координаты точки М равны соответствующим координатам ее радиус-вектора
Слайд 4
х
у
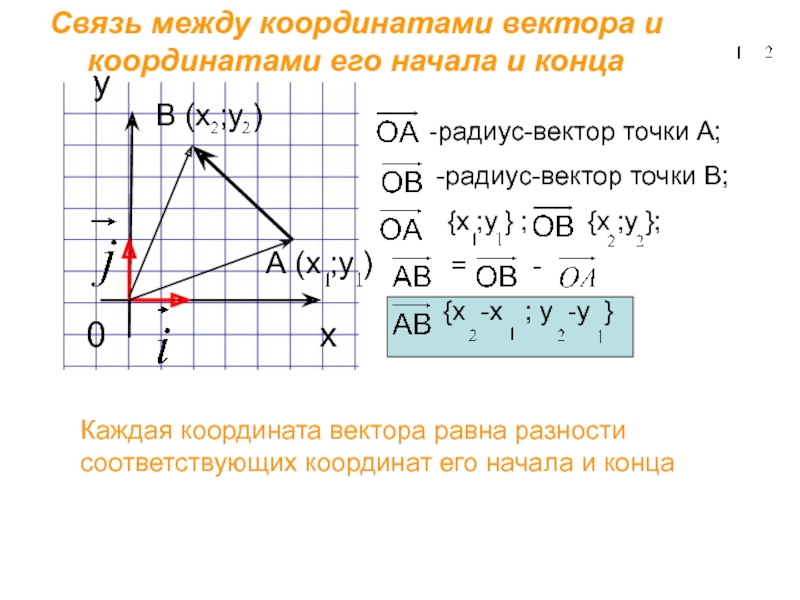
Связь между координатами вектора и координатами его начала и конца
А (х
;у )
0
-радиус-вектор точки А;
-радиус-вектор точки В;
{х ;у } ; {х ;у };
= -
{х -х ; у -у }
Каждая координата вектора равна разности соответствующих координат его начала и конца
В (х ;у )
Слайд 5
х
у
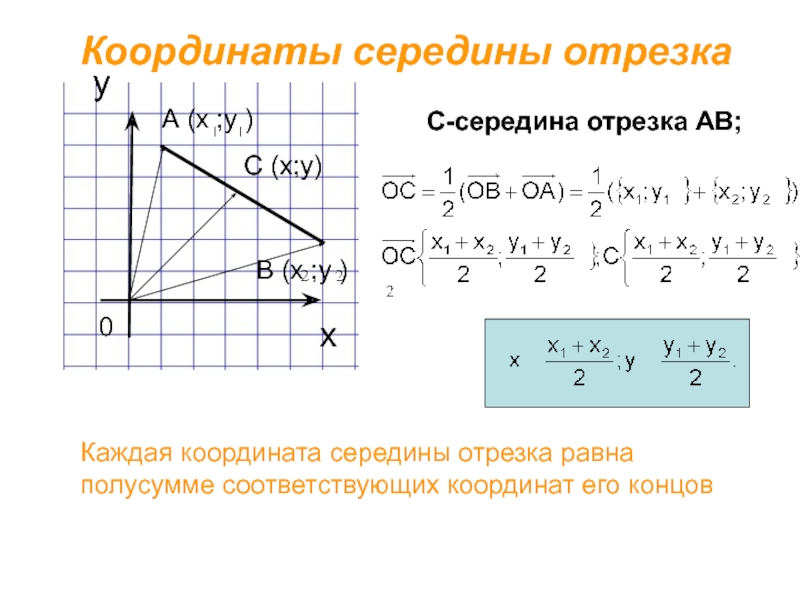
Координаты середины отрезка
С (х;у)
0
Каждая координата середины отрезка равна полусумме соответствующих координат
его концов
В (х ;у )
А (х ;у )
С-середина отрезка АВ;
Слайд 10Проверь свои знания
Что такое радиус-вектор точки?
Как вычислить координаты вектора по координатам
его начала и конца?
Как вычислить координаты середины отрезка по координатам его начала и конца?
Как найти длину отрезка по его координатам?
Как вычислить расстояние между двумя точками по их координатам?
Как вычислить координаты середины отрезка по координатам его начала и конца?
Как найти длину отрезка по его координатам?
Как вычислить расстояние между двумя точками по их координатам?
