движение, при котором все точки тела движутся в плоскостях, параллельных одной неподвижной плоскости, которая называется основной плоскостью.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Плоскопараллельное движение твердого тела (плоское) презентация
Содержание
- 1. Плоскопараллельное движение твердого тела (плоское)
- 2. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ Основная
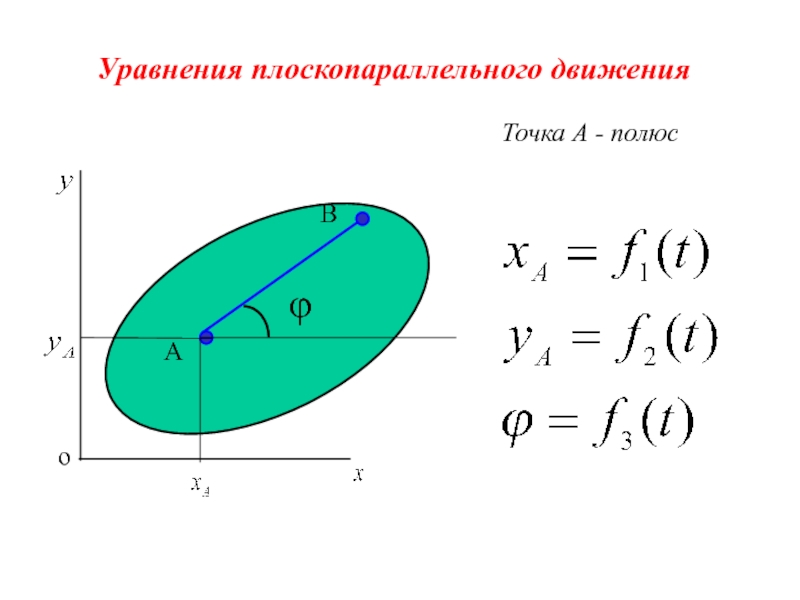
- 3. Уравнения плоскопараллельного движения A φ B Точка А - полюс
- 4. Пример плоскопараллельного движения твердого тела
- 5. Разложение плоскопараллельного движения на простейшие виды движения
- 6. Геометрическая интерпретация теоремы А В
- 7. Теорема о проекциях скоростей двух точек тела
- 8. P A B Точка P –
- 9. Соотношения между скоростями точек тела и угловой
- 10. Скорости двух точек тела параллельны друг другу,
- 11. Скорости двух точек параллельны, но не перпендикулярны
- 12. 4. Тело катится без скольжения по неподвижной поверхности. ω
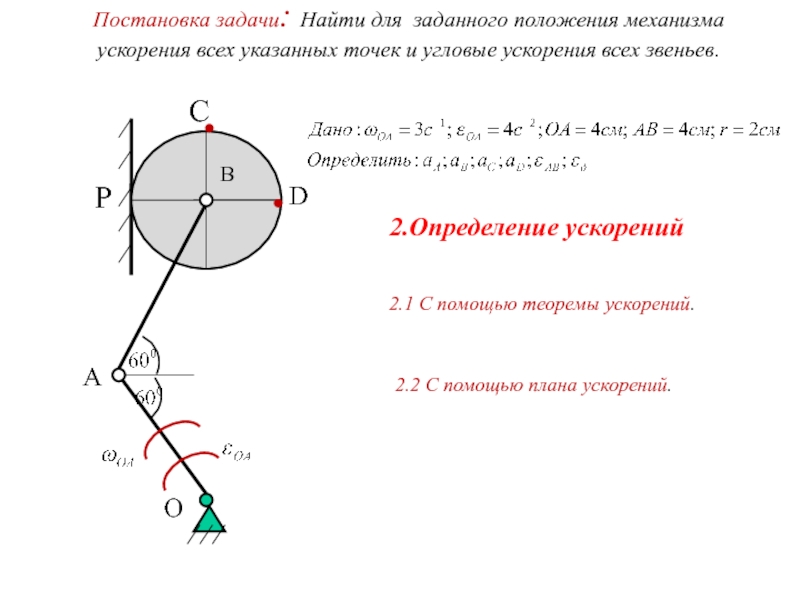
- 14. Постановка задачи: Найти для заданного положения
- 15. Для заданного положения механизма определить скорости
- 16. 3.Определение скоростей с помощью мгновенного центра
- 17. A D O
- 18. Свойства плана скоростей Одноименные отрезки плана скоростей
- 19. Правило оформления ИДЗ К.
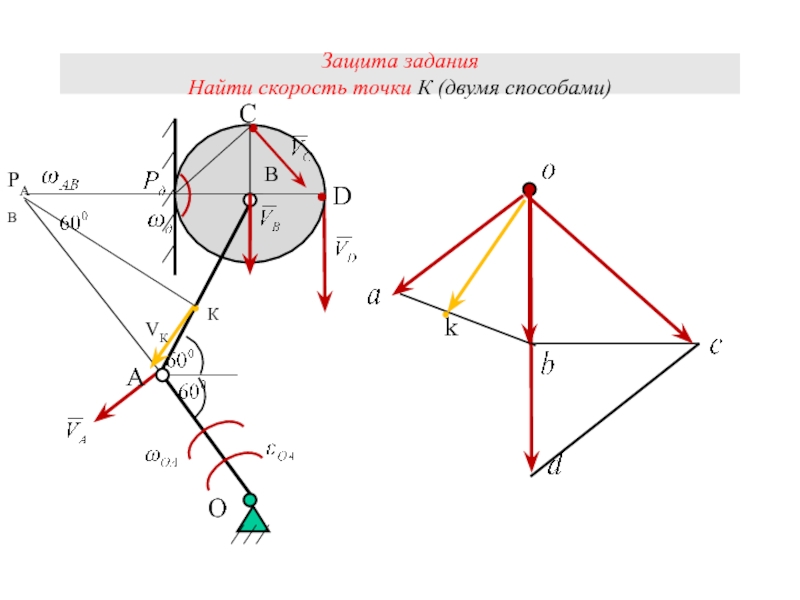
- 20. Защита задания Найти скорость точки К (двумя
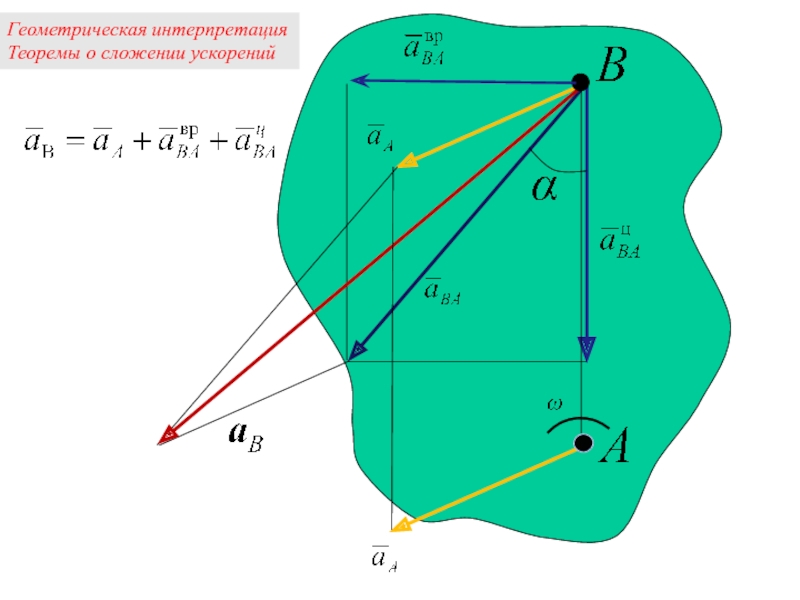
- 21. Теорема о сложении ускорений точек при плоскопараллельном
- 22. Геометрическая интерпретация Теоремы о сложении ускорений
- 23. Постановка задачи: Найти для заданного положения механизма
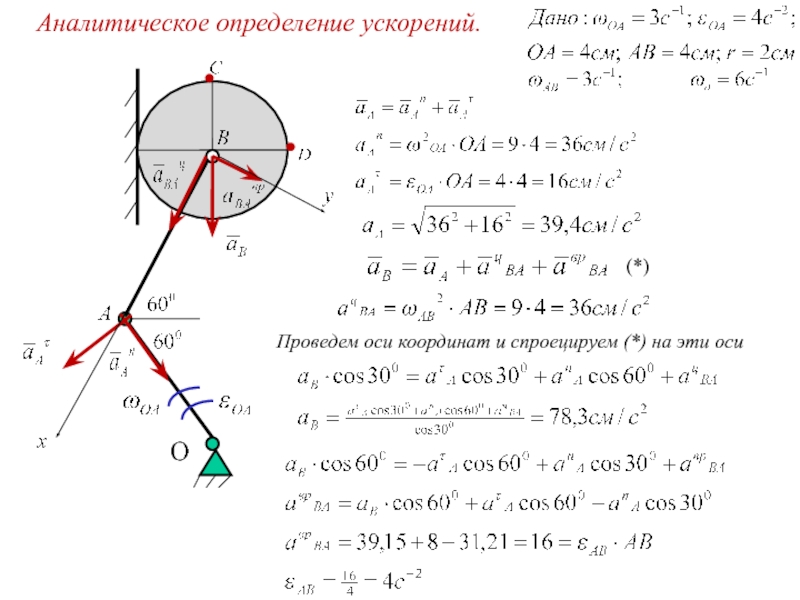
- 24. Аналитическое определение ускорений.
- 25. Найти ускорения всех указанных точек и угловое
- 26. Пример определения ускорения точки В, когда не
- 27. Свойства плана ускорений 1. Одноименные отрезки плана
- 28. План ускорений Графическое изображение векторов ускорений точек
- 29. Защита. Найти ускорение точки М или точки
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ Основная плоскость A B C А1 В1 D Рассмотрим произвольное сечение. Произвольные точки сечения А и B спроецируем
Слайд 1Плоскопараллельное движение твердого тела (плоское)
Плоскопараллельным (плоским) движением твердого тела называется такое
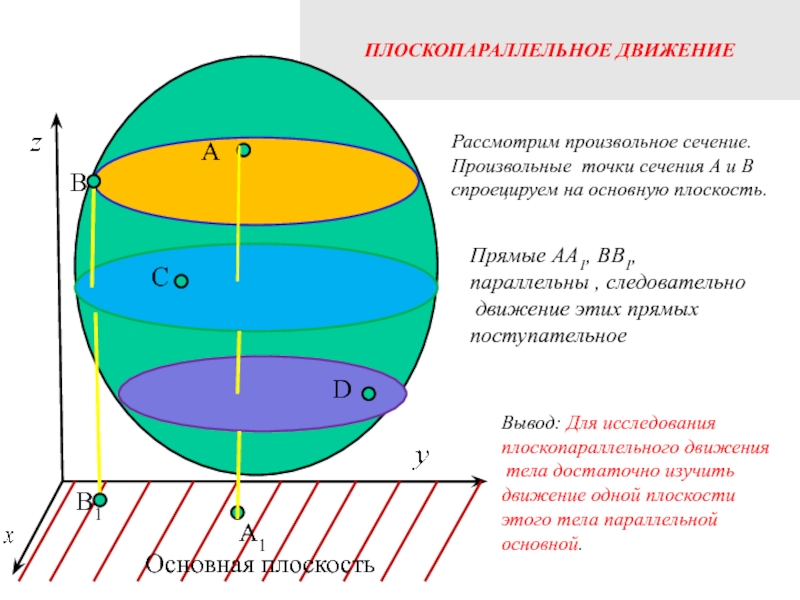
Слайд 2ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
Основная плоскость
A
B
C
А1
В1
D
Рассмотрим произвольное сечение.
Произвольные точки сечения А и B
спроецируем на основную плоскость.
Вывод: Для исследования
плоскопараллельного движения
тела достаточно изучить
движение одной плоскости
этого тела параллельной основной.
Прямые АА1, ВВ1,
параллельны , следовательно
движение этих прямых
поступательное
Слайд 5Разложение плоскопараллельного движения на простейшие виды движения
φ
φ
А
В
А1
В1
В2
А2
Было АВ
k
Угол φ не зависит
от выбора полюса
Стало А1В1
Плоскопараллельное движение можно разложить на поступательное
движение вместе с полюсом и вращательное вокруг оси,
проходящей через полюс.
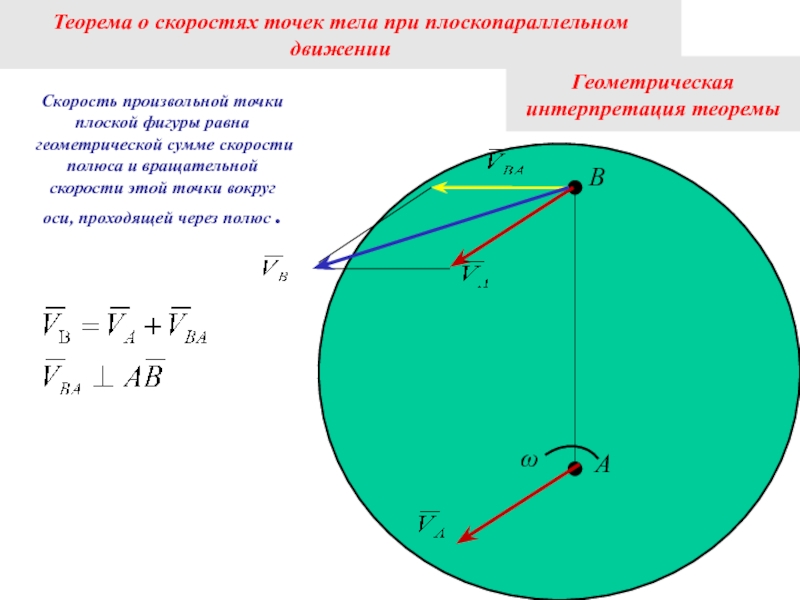
Слайд 6Геометрическая интерпретация теоремы
А
В
ω
Скорость произвольной точки плоской фигуры равна геометрической сумме
скорости полюса и вращательной скорости этой точки вокруг оси, проходящей через полюс .
Теорема о скоростях точек тела при плоскопараллельном движении
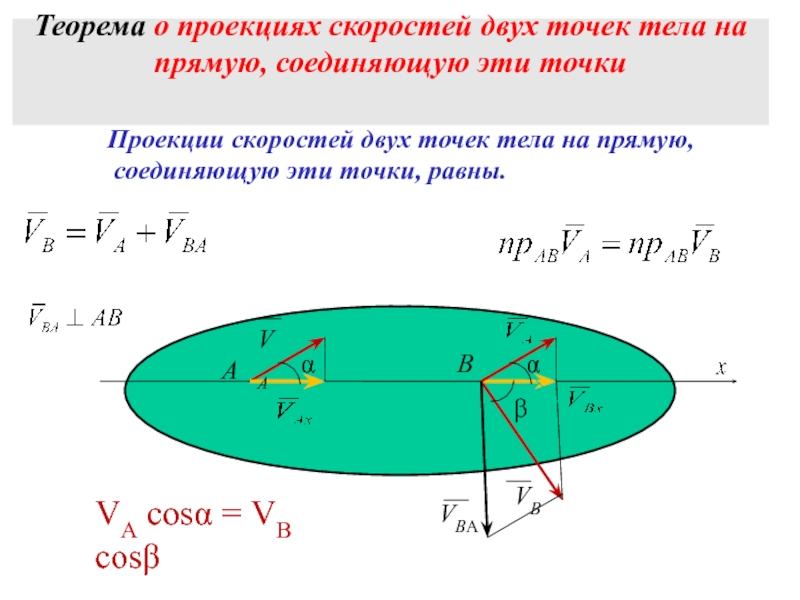
Слайд 7Теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти
точки
A
B
VA
VB
VBA
α
β
VA cosα = VB cosβ
Проекции скоростей двух точек тела на прямую,
соединяющую эти точки, равны.
α
Слайд 8
P
A
B
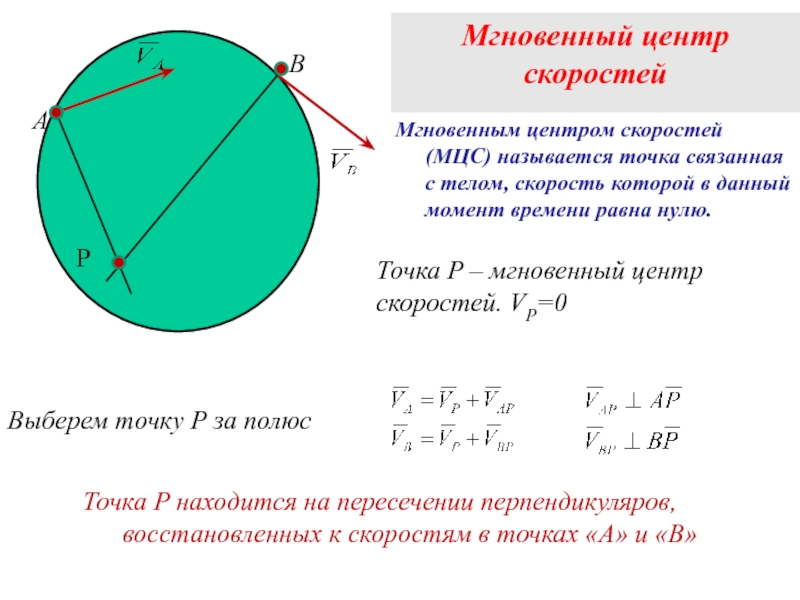
Точка P – мгновенный центр
скоростей. VP=0
Точка P находится на пересечении перпендикуляров,
восстановленных к скоростям в точках «А» и «В»
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка связанная с телом, скорость которой в данный момент времени равна нулю.
Выберем точку P за полюс
Слайд 9Соотношения между скоростями точек тела и угловой скоростью
Вывод
Плоскопараллельное движение можно рассматривать
как
мгновенное вращение вокруг мгновенной оси
(ось, проходящая через МЦС).
(ось, проходящая через МЦС).
P
A
B
VB
С
Скорости точек прямо пропорциональны расстояниям от точек до МЦС
Угловая скорость тела равна отношению
скорости любой точки тела на расстояние
от этой точки до МЦС.
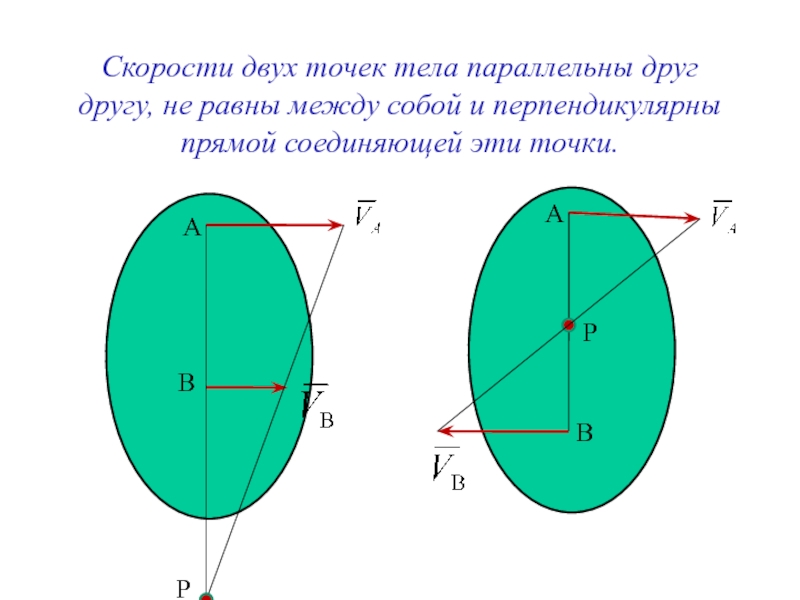
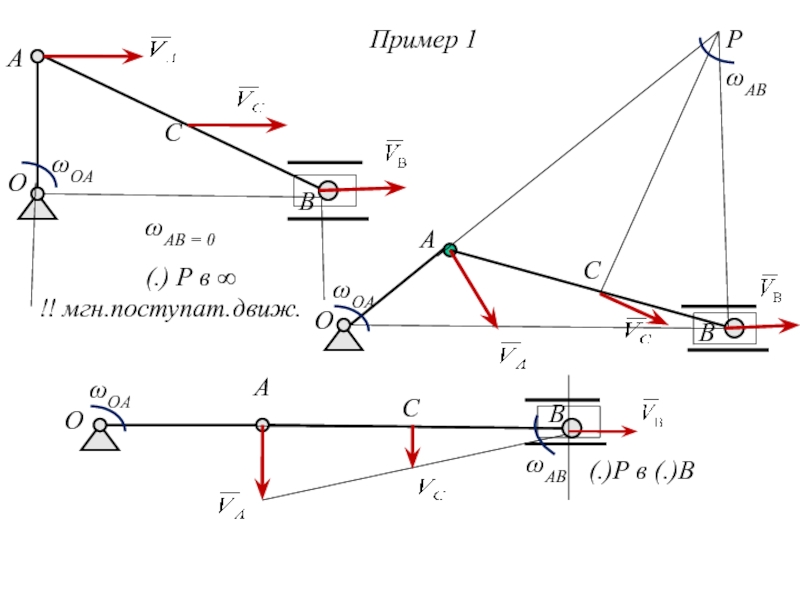
Слайд 10Скорости двух точек тела параллельны друг другу, не равны между собой
и перпендикулярны прямой соединяющей эти точки.
А
В
А
В
Р
Р
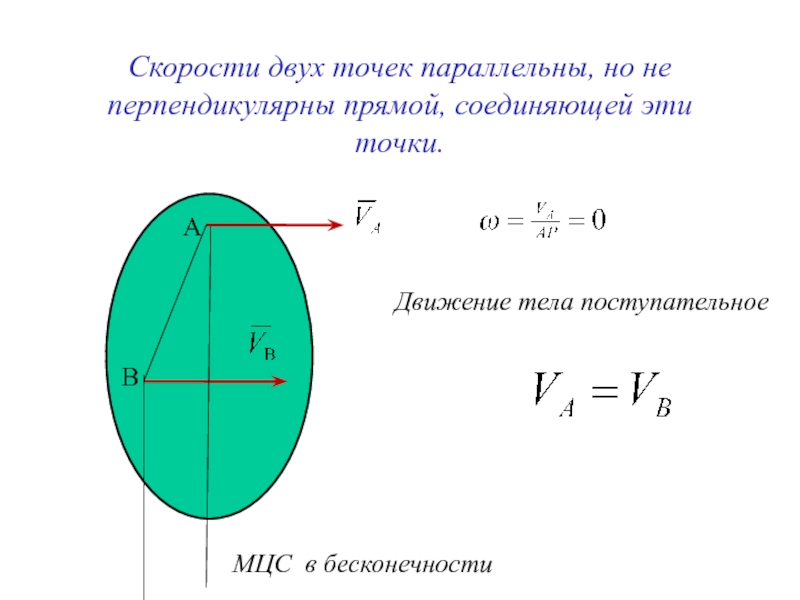
Слайд 11Скорости двух точек параллельны, но не перпендикулярны прямой, соединяющей эти точки.
А
В
МЦС
в бесконечности
Движение тела поступательное
Слайд 14Постановка задачи: Найти для заданного положения механизма скорости, указанных точек, угловые
скорости всех звеньев и ускорения двух точек.
A
D
O
В
с
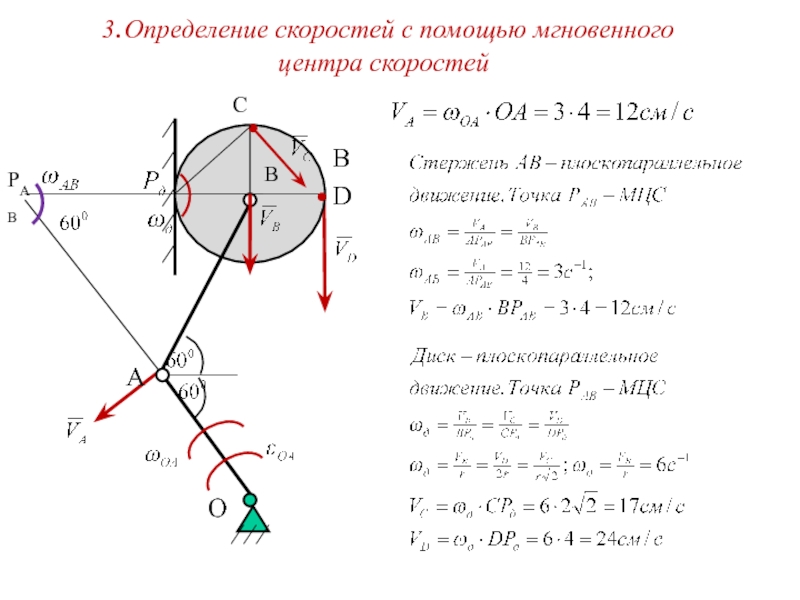
1.1 С помощью мгновенного центра скоростей.
1.Определение скоростей
1.2 С помощью плана скоростей.
2.Определение ускорений
2.1 С помощью теоремы ускорений.
В
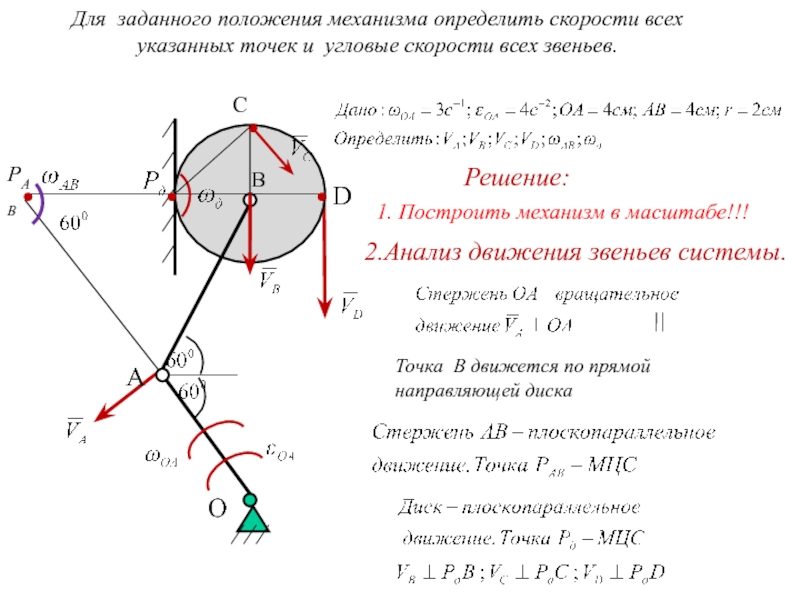
Слайд 15 Для заданного положения механизма определить скорости всех указанных точек и угловые
скорости всех звеньев.
С
PAB
Решение:
2.Анализ движения звеньев системы.
A
D
O
В
В
Точка В движется по прямой
направляющей диска
1. Построить механизм в масштабе!!!
Слайд 17
A
D
O
В
В
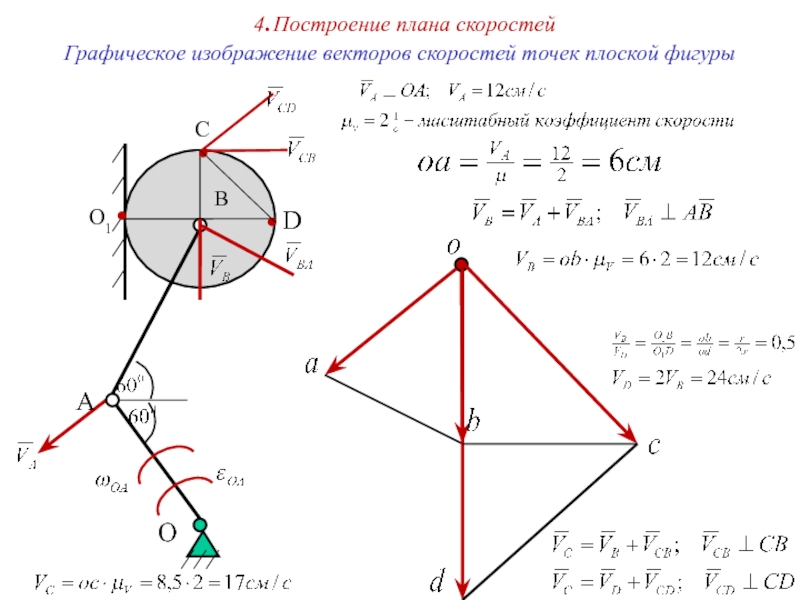
4.Построение плана скоростей
Графическое изображение векторов скоростей точек плоской фигуры
О1
С
Слайд 18Свойства плана скоростей
Одноименные отрезки плана скоростей и механизма
взаимно перпендикулярны.
2. Одноименные
отрезки плана скоростей и механизма
прямо пропорциональны.
прямо пропорциональны.
3. Одноименные фигуры плана скоростей и механизма подобны
и повернуты друг относительно друга на угол 900
Слайд 19Правило оформления ИДЗ К.
Титульный лист.
«Кинематический анализ плоского механизма.»
Формат отчета: А4
Лист 1. Схема механизма. Постановка задачи. Дано.
Лист 2. Схема механизма в масштабе.
Аналитическое определение скоростей (МЦС) и ускорений.
4. Лист 3. Схема механизма в масштабе.
Графическое определение скоростей (план скоростей).
«Кинематический анализ плоского механизма.»
Формат отчета: А4
Лист 1. Схема механизма. Постановка задачи. Дано.
Лист 2. Схема механизма в масштабе.
Аналитическое определение скоростей (МЦС) и ускорений.
4. Лист 3. Схема механизма в масштабе.
Графическое определение скоростей (план скоростей).
Слайд 21Теорема о сложении ускорений точек при плоскопараллельном движении тела
Ускорение произвольной точки
тела
при его плоскопараллельном движении равно
векторной сумме ускорения полюса, вращательного и центростремительного ускорений этой точки при вращении вокруг полюса.
при его плоскопараллельном движении равно
векторной сумме ускорения полюса, вращательного и центростремительного ускорений этой точки при вращении вокруг полюса.
Слайд 23Постановка задачи: Найти для заданного положения механизма ускорения всех указанных точек
и угловые ускорения всех звеньев.
A
D
O
В
С
2.Определение ускорений
2.1 С помощью теоремы ускорений.
2.2 С помощью плана ускорений.
В
P
Слайд 25Найти ускорения всех указанных точек и угловое ускорение диска.
В
Спроецируем (*) на
оси координат
(*)
Аналогично определяем ускорение (.) С
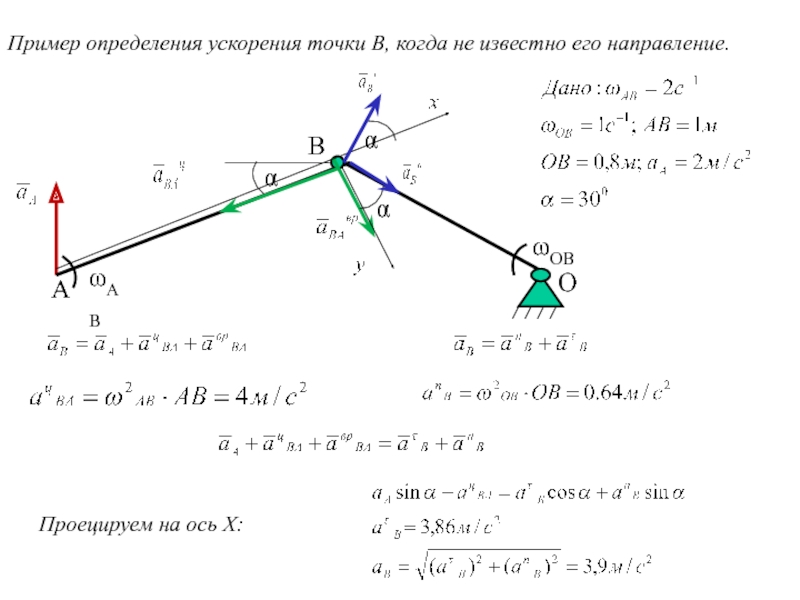
Слайд 26Пример определения ускорения точки В, когда не известно его направление.
α
ωAB
А
В
α
ωOB
Проецируем
на ось X:
α
О
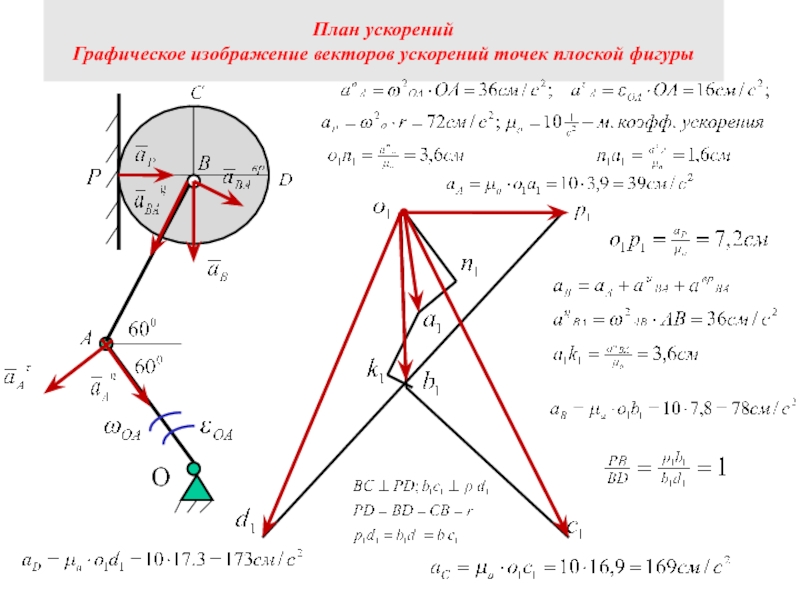
Слайд 27Свойства плана ускорений
1. Одноименные отрезки плана ускорений и механизма прямо пропорциональны.
2. Одноименные фигуры плана ускорений и механизма подобны.
Одноименные отрезки плана ускорений и механизма подобны и одноименные фигуры плана ускорений и механизма повернуты друг относительно друга на угол α = arctg(ԑ/ω2) , где ԑ и ω соответствующего звена механизма
Построение плана ускорений.
