- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи №№ 5-21. Геометрия презентация
Содержание
- 1. Задачи №№ 5-21. Геометрия
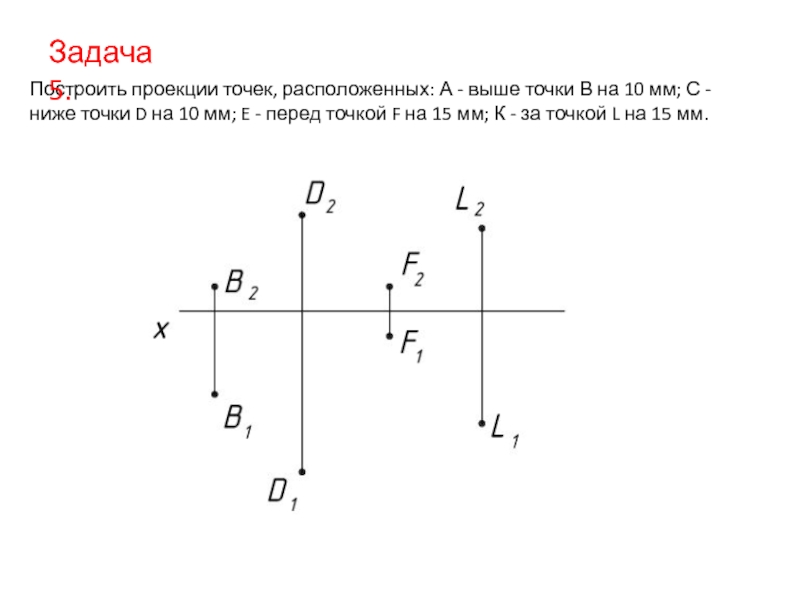
- 2. Построить проекции точек, расположенных: А - выше
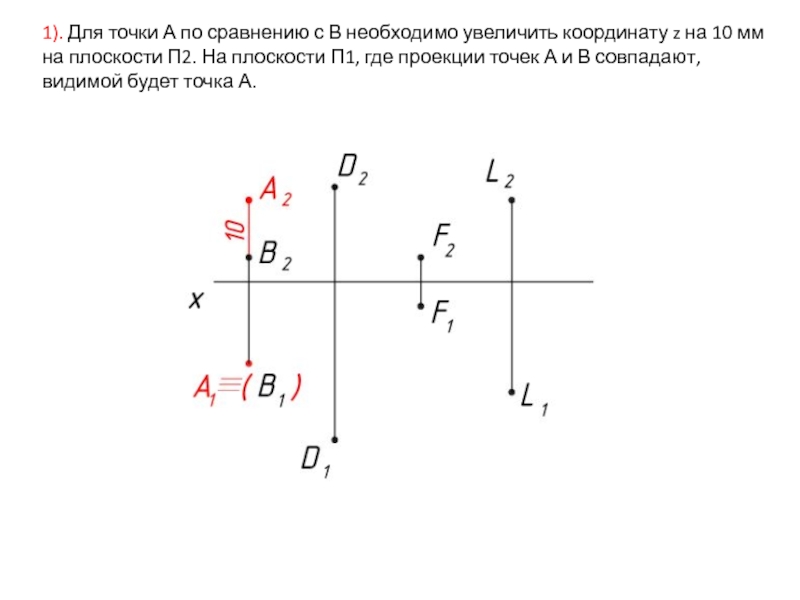
- 3. 1). Для точки А по сравнению с
- 4. 2). Для точки С по сравнению с
- 5. 3). Для точки E по сравнению с
- 6. 4). Для точки K по сравнению с
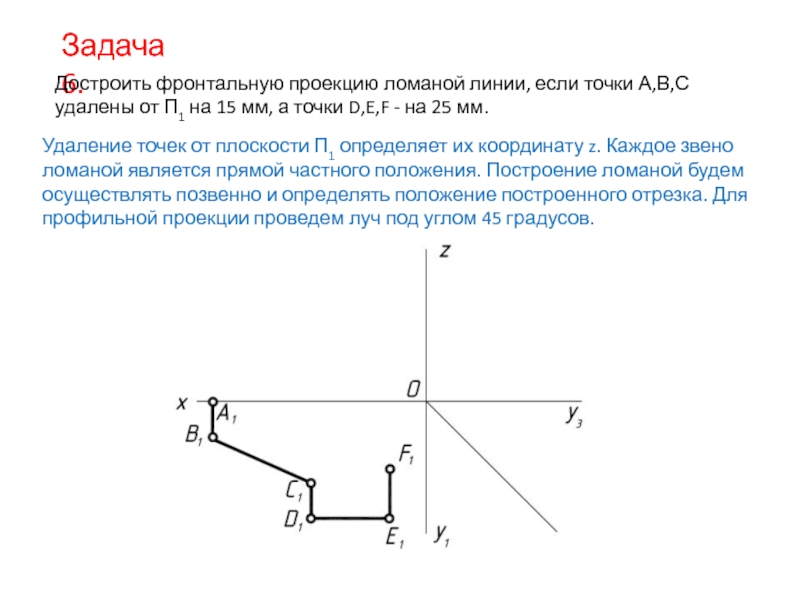
- 7. Задача 6. Достроить фронтальную проекцию ломаной линии,
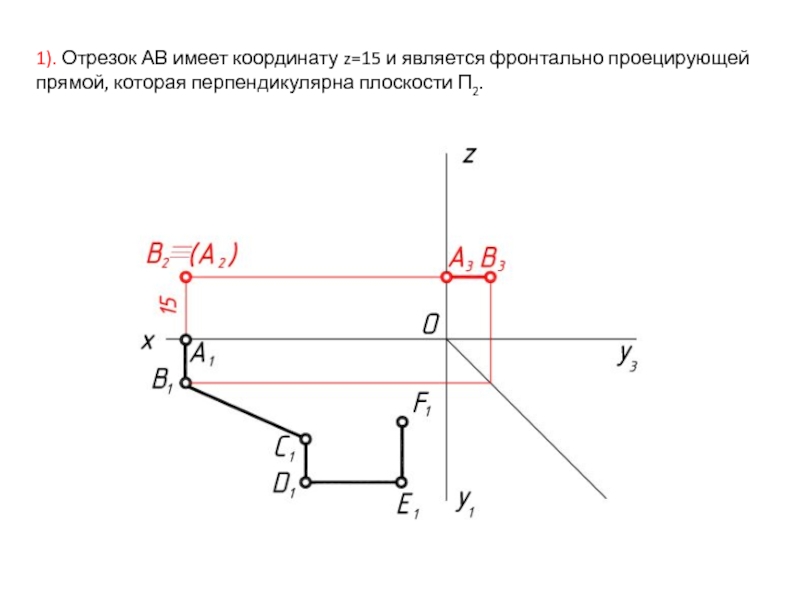
- 8. 1). Отрезок АВ имеет координату z=15 и является фронтально проецирующей прямой, которая перпендикулярна плоскости П2.
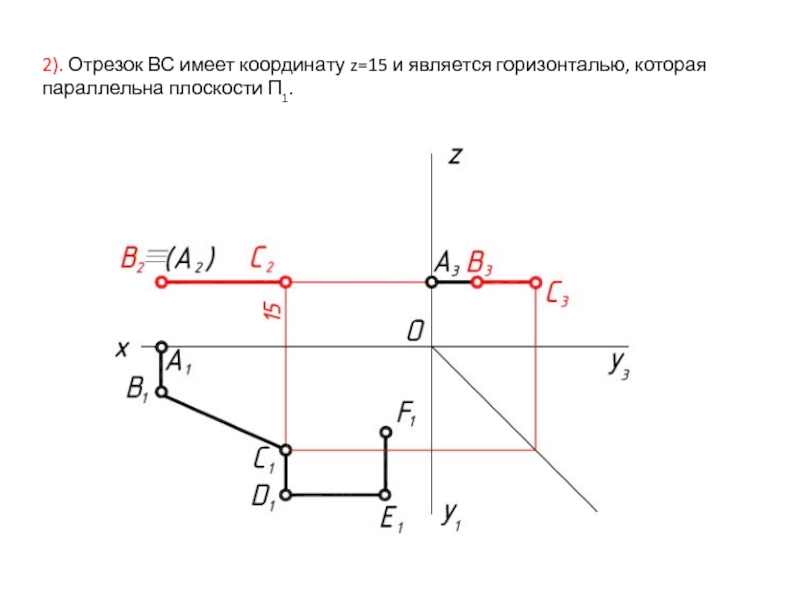
- 9. 2). Отрезок ВС имеет координату z=15 и является горизонталью, которая параллельна плоскости П1.
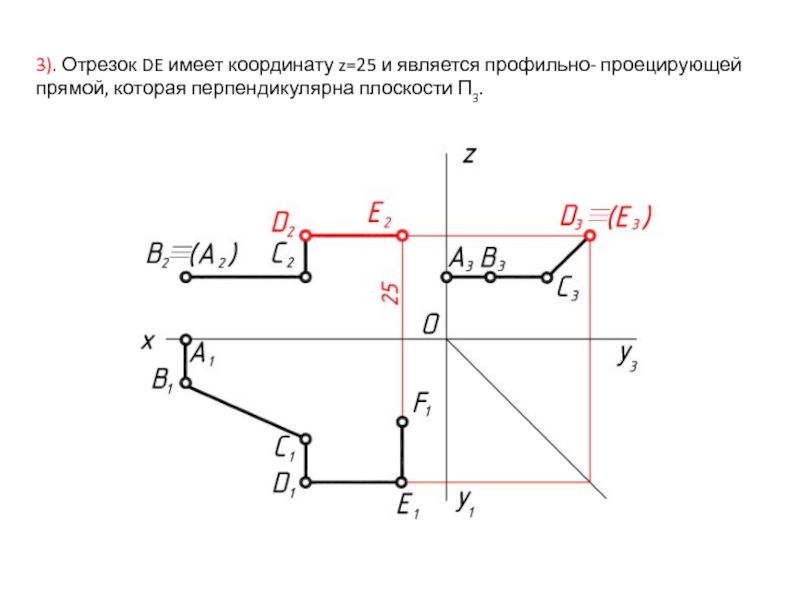
- 10. 3). Отрезок DE имеет координату z=25 и является профильно- проецирующей прямой, которая перпендикулярна плоскости П3.
- 11. 4). Отрезок EF имеет координату z=25 и является фронтально проецирующей прямой, которая перпендикулярна плоскости П2.
- 12. Задача 7. Через точку А провести отрезок
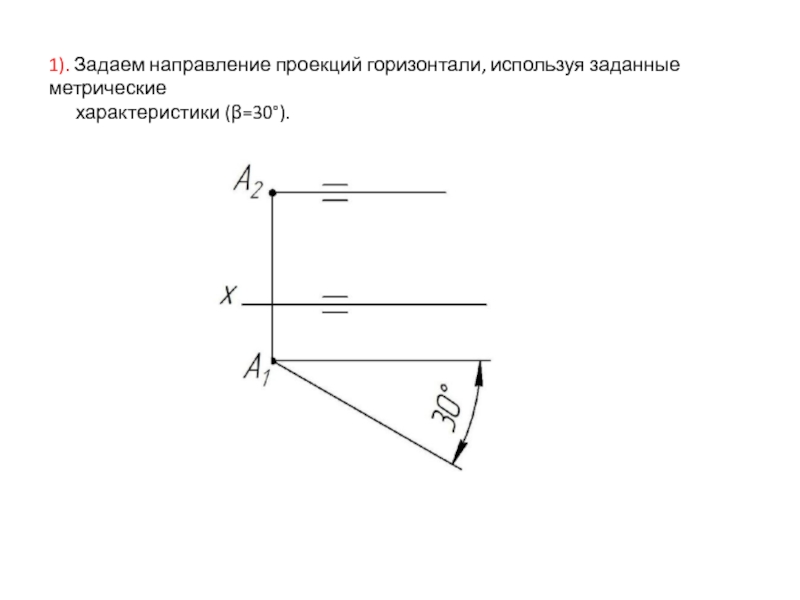
- 13. 1). Задаем направление проекций горизонтали, используя заданные метрические характеристики (β=30°).
- 14. 2). На горизонтальной проекции откладываем натуральную величину
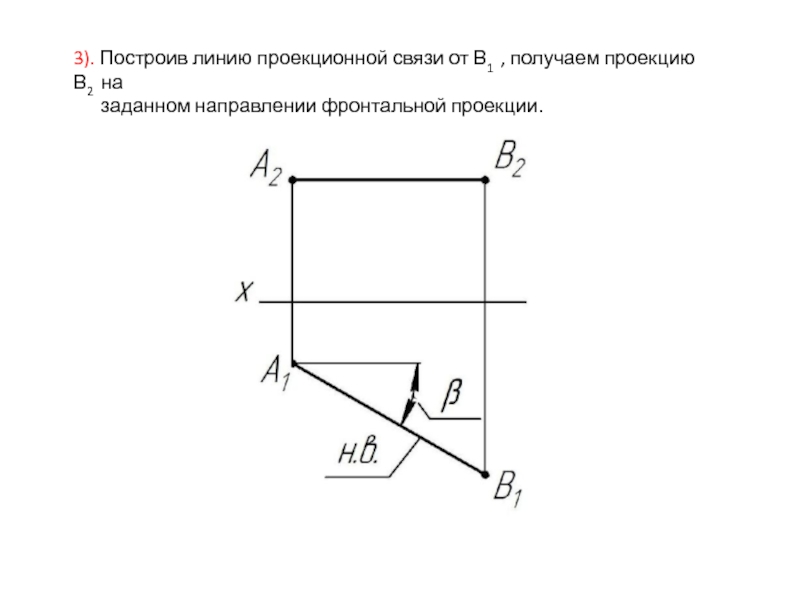
- 15. 3). Построив линию проекционной связи от В1
- 16. Задача 10. Определить длину отрезка АВ прямой
- 17. 1). Введем дополнительную плоскость проекций П4 перпендикулярно
- 18. 2). В силу ортогональности метода проецирования линии
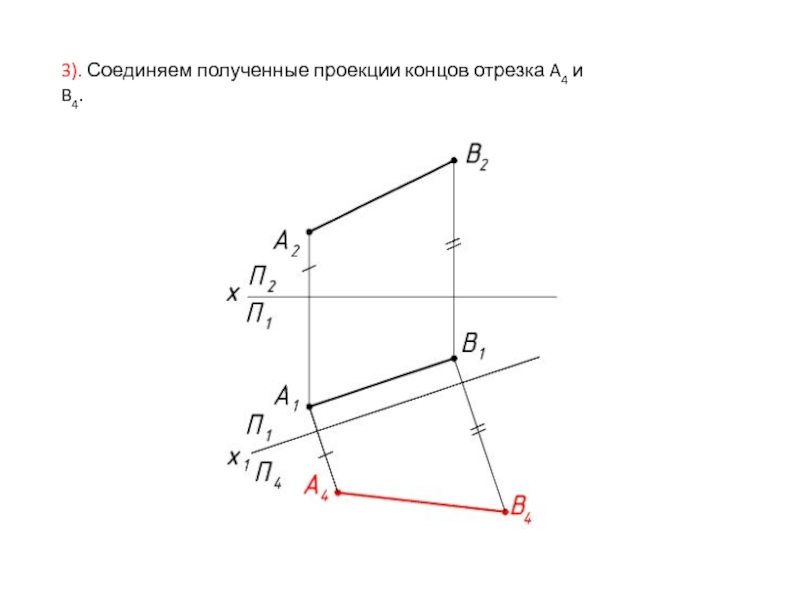
- 19. 3). Соединяем полученные проекции концов отрезка A4 и B4.
- 20. 4). На плоскости П4 имеем натуральную величину
- 21. 5). Введем новую дополнительную плоскость П5 перпендикулярно
- 22. 6). Линии связи проводим перпендикулярно x2 и
- 23. 7). Соединяем проекции концов отрезка A5 и
- 24. Переменой плоскости проекций перевести отрезок АВ горизонтали в проецирующее положение. Задача 12.
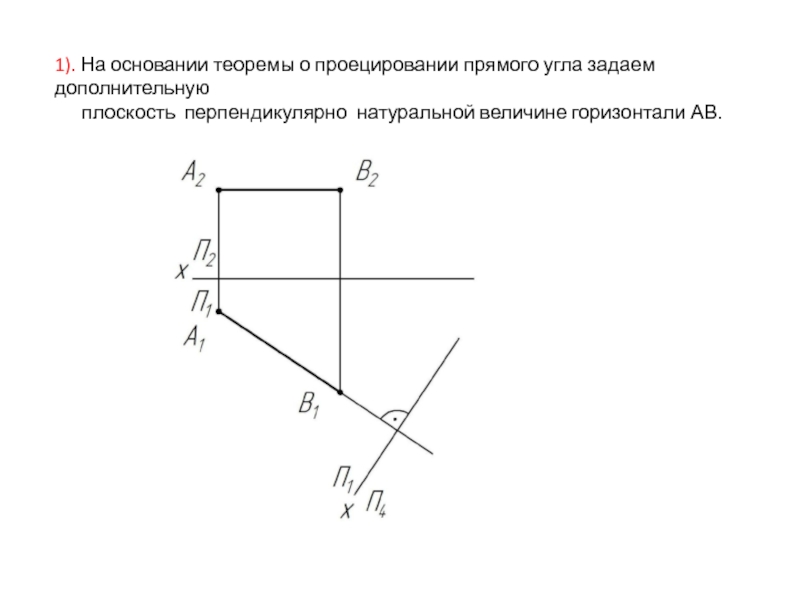
- 25. 1). На основании теоремы о проецировании прямого
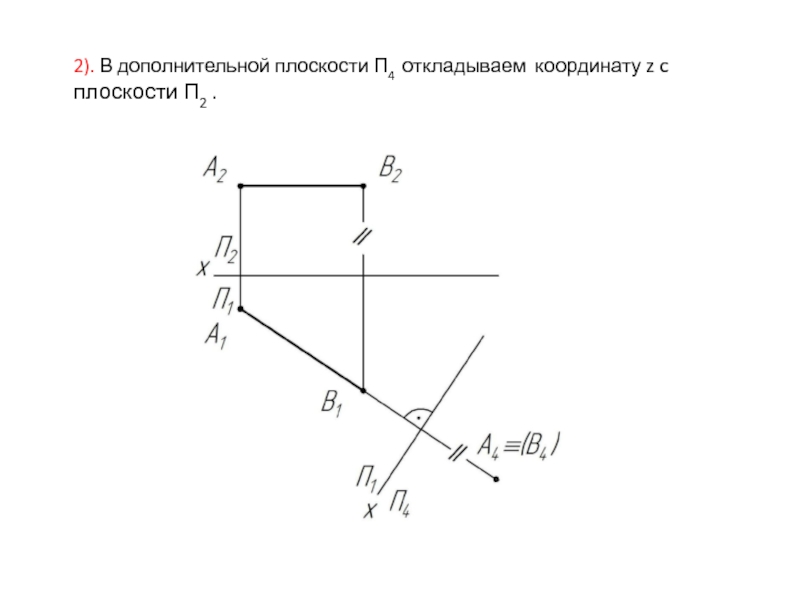
- 26. 2). В дополнительной плоскости П4 откладываем координату z c плоскости П2 .
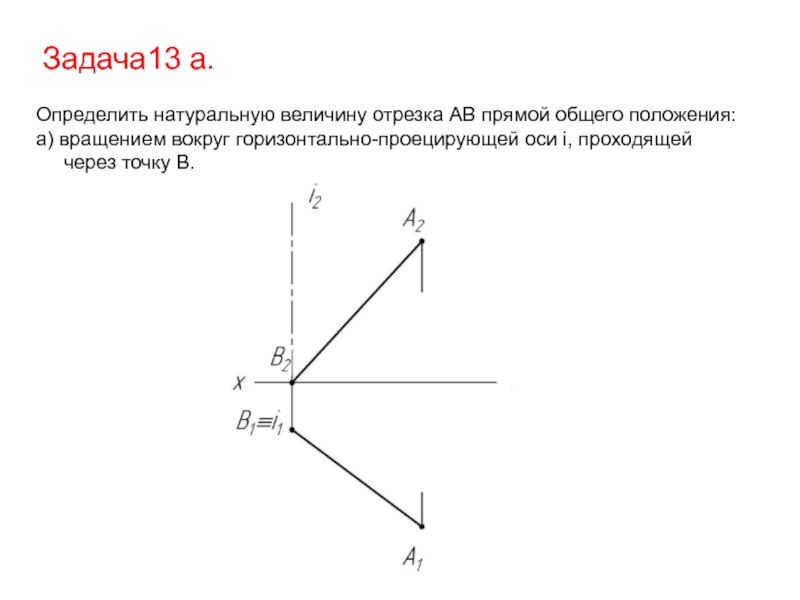
- 27. Задача13 а. Определить натуральную величину отрезка АВ
- 28. 1). Вращаем прямую общего положения до
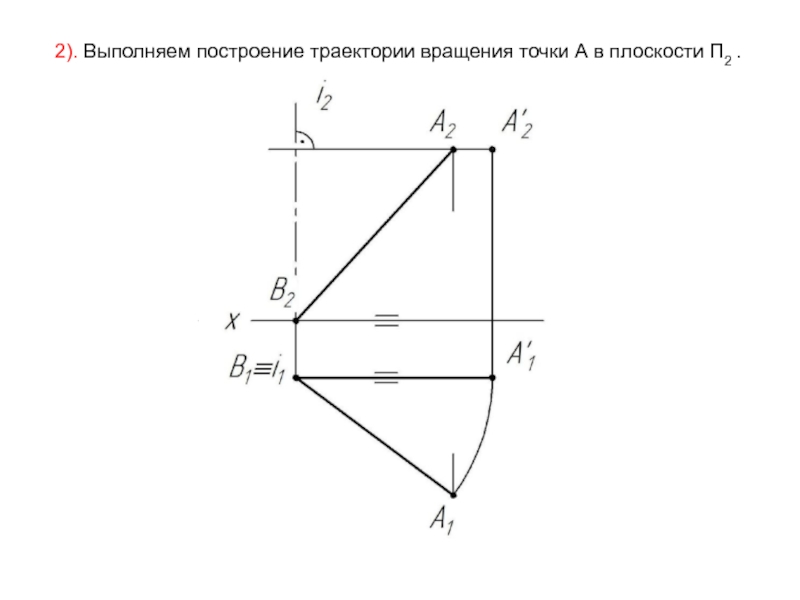
- 29. 2). Выполняем построение траектории вращения точки А в плоскости П2 .
- 30. 3). Соединяем полученные проекции точки А с
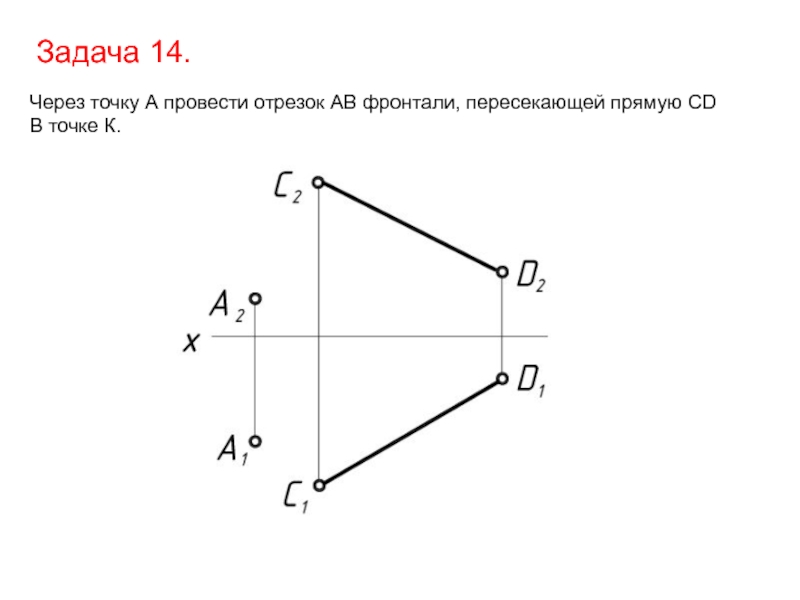
- 31. Задача 14. Через точку А провести отрезок АВ фронтали, пересекающей прямую СD В точке К.
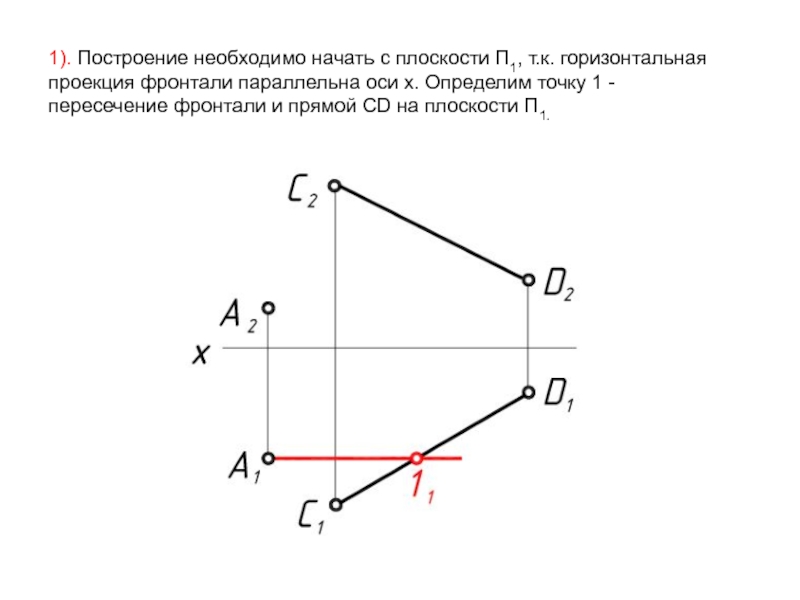
- 32. 1). Построение необходимо начать с плоскости П1,
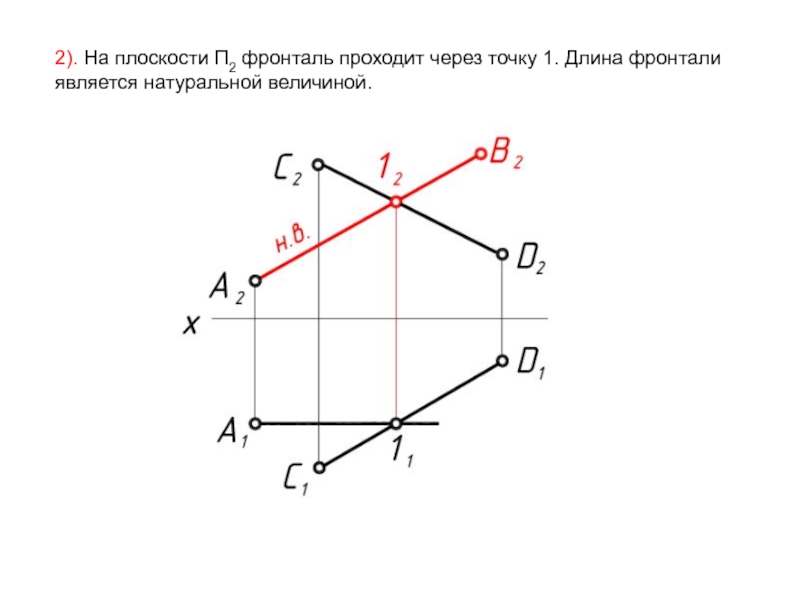
- 33. 2). На плоскости П2 фронталь проходит через точку 1. Длина фронтали является натуральной величиной.
- 34. 3). Длина горизонтальной проекции фронтали определяется по линии связи проекций точки В.
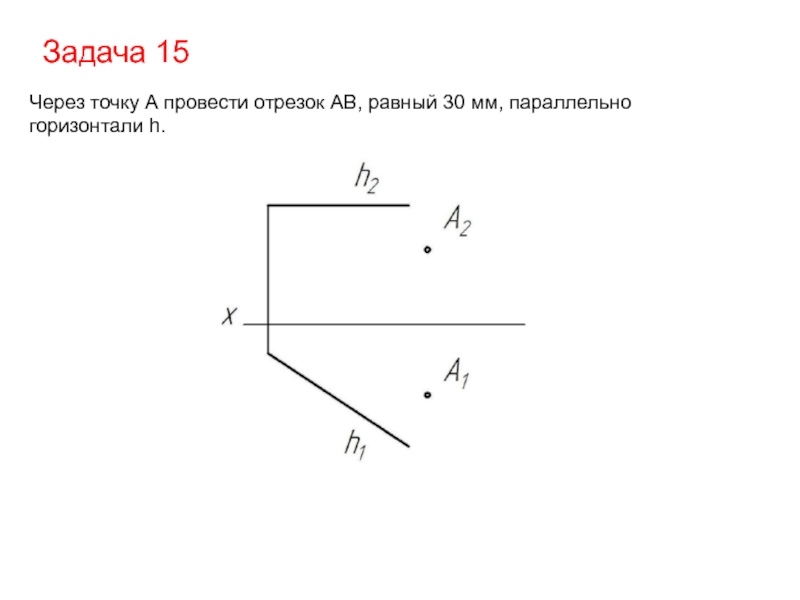
- 35. Задача 15 Через точку А провести отрезок АВ, равный 30 мм, параллельно горизонтали h.
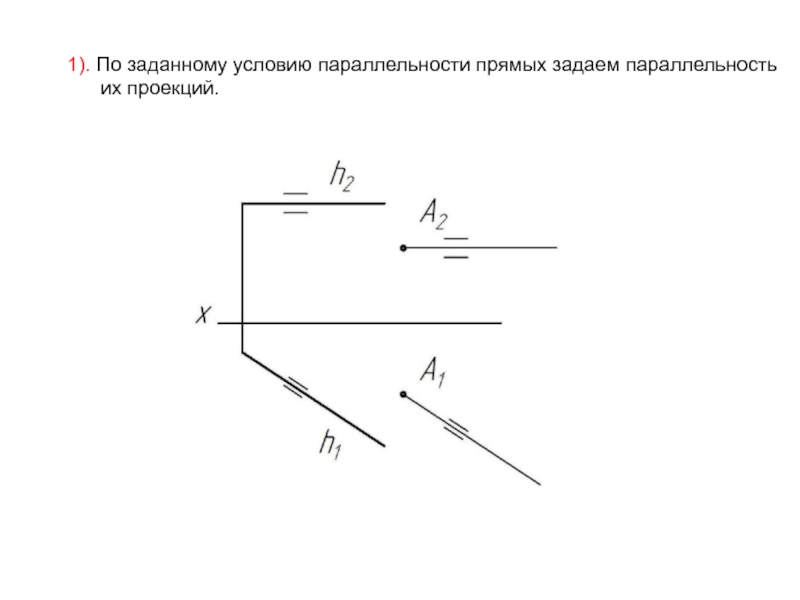
- 36. 1). По заданному условию параллельности прямых задаем параллельность их проекций.
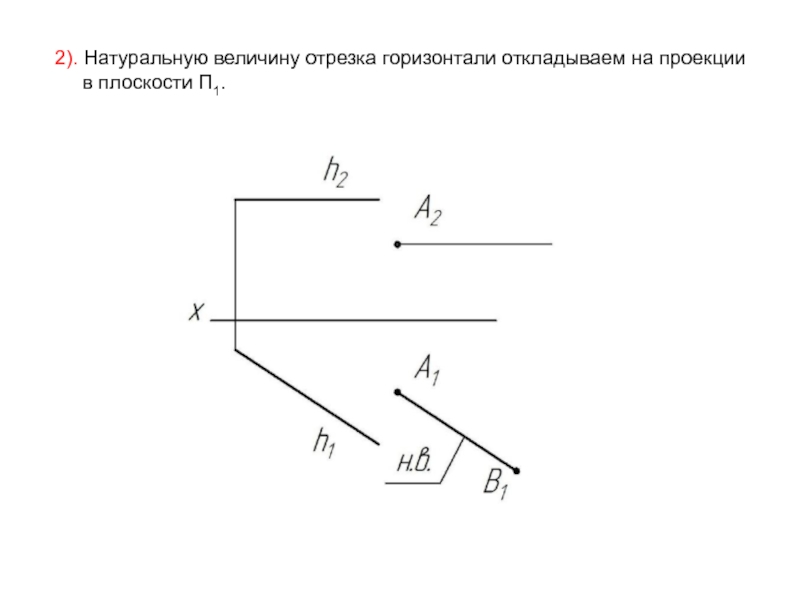
- 37. 2). Натуральную величину отрезка горизонтали откладываем на проекции в плоскости П1.
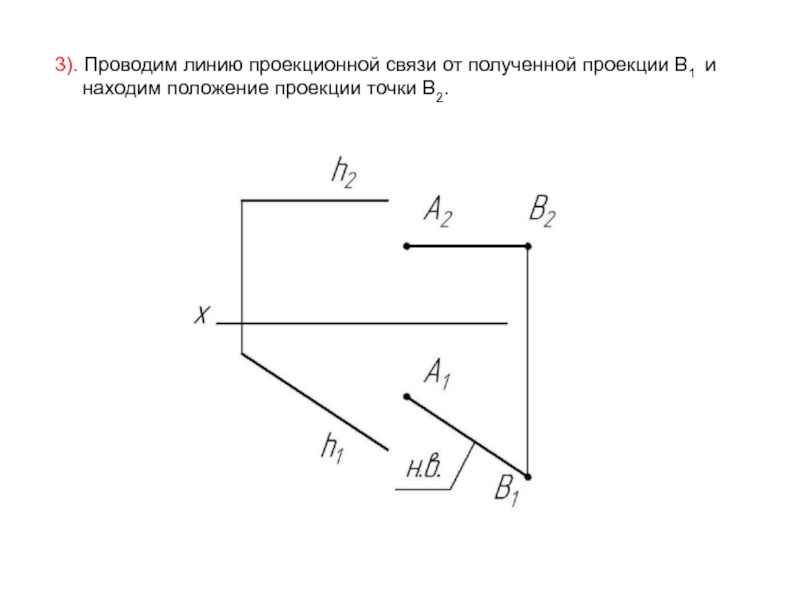
- 38. 3). Проводим линию проекционной связи от полученной
- 39. Задача 16 Определить взаимное расположение прямых a
- 40. 1). Проводим проекции прямых в каждой плоскости проекций до их пересечения.
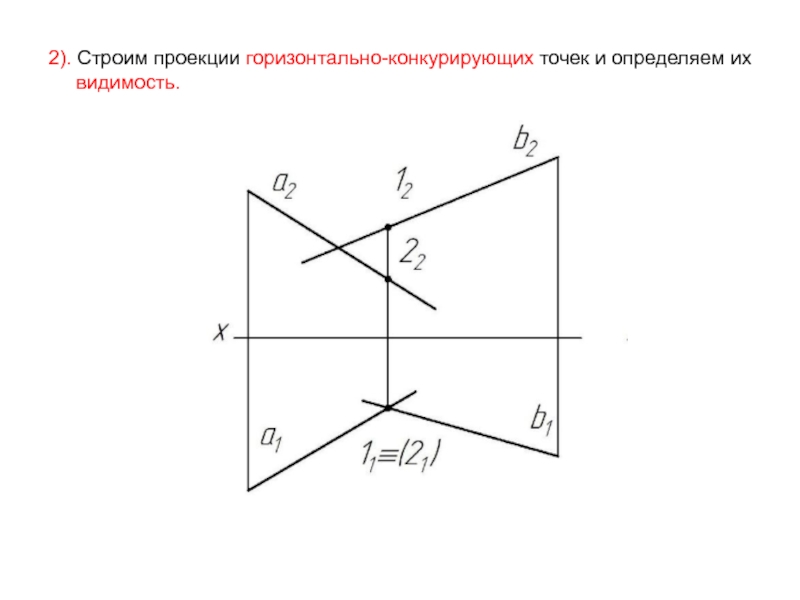
- 41. 2). Строим проекции горизонтально-конкурирующих точек и определяем их видимость.
- 42. 3). Строим проекции фронтально-конкурирующих точек и определяем их видимость.
- 43. Задача 17. Показать видимость сторон треугольников, образующих двугранный угол при стороне AD.
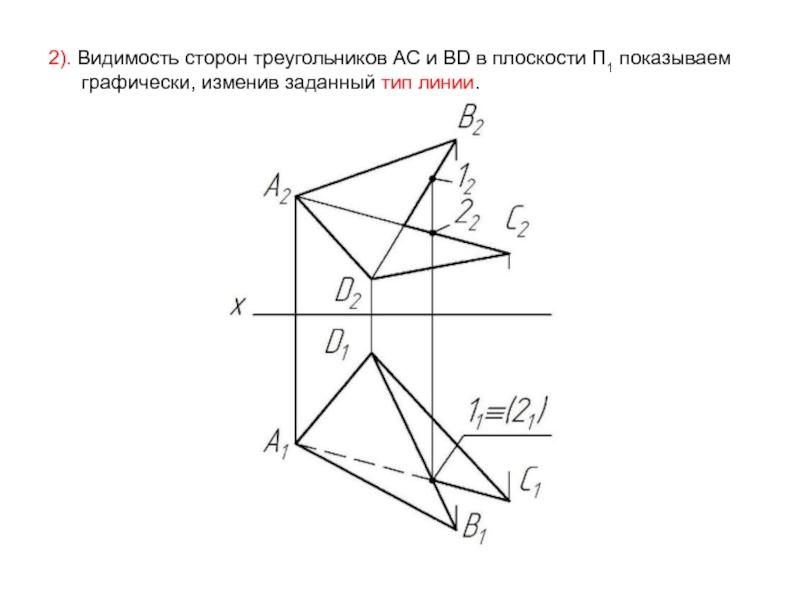
- 44. 1). Определяем видимость сторон треугольников в плоскости
- 45. 2). Видимость сторон треугольников AC и BD
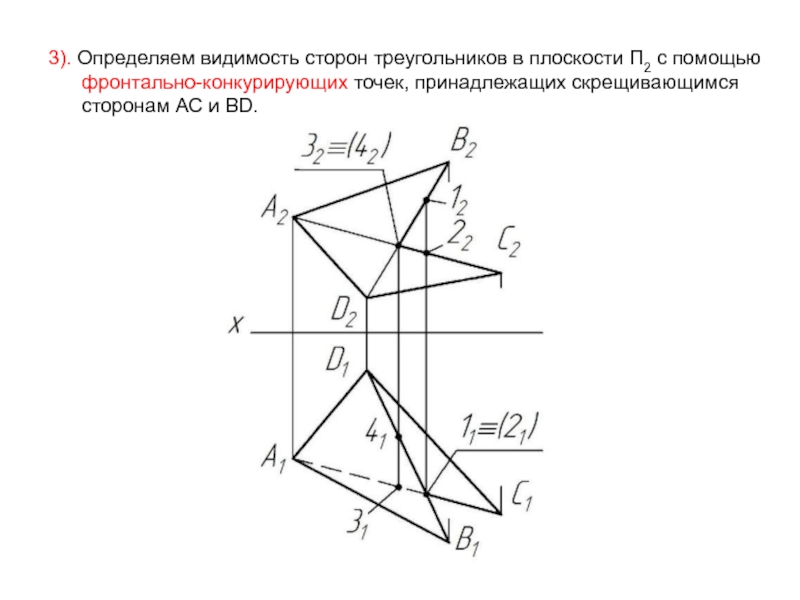
- 46. 3). Определяем видимость сторон треугольников в плоскости
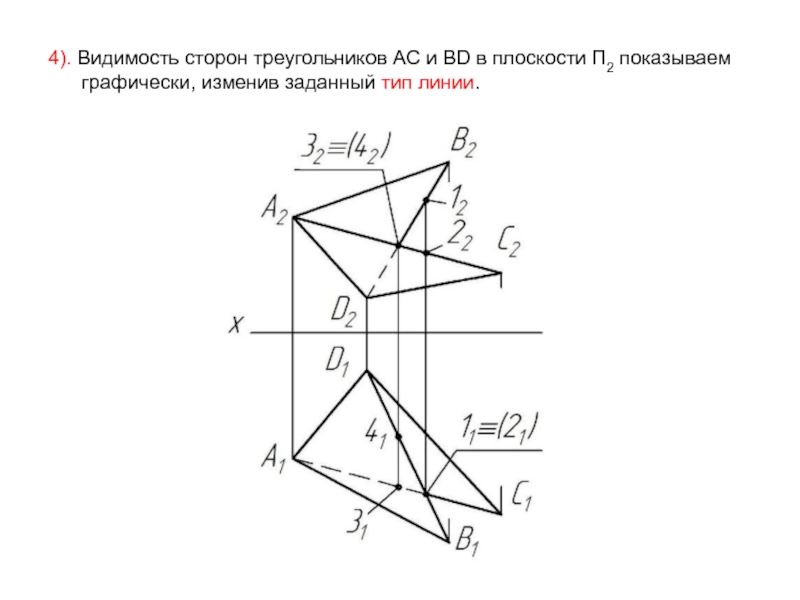
- 47. 4). Видимость сторон треугольников AC и BD
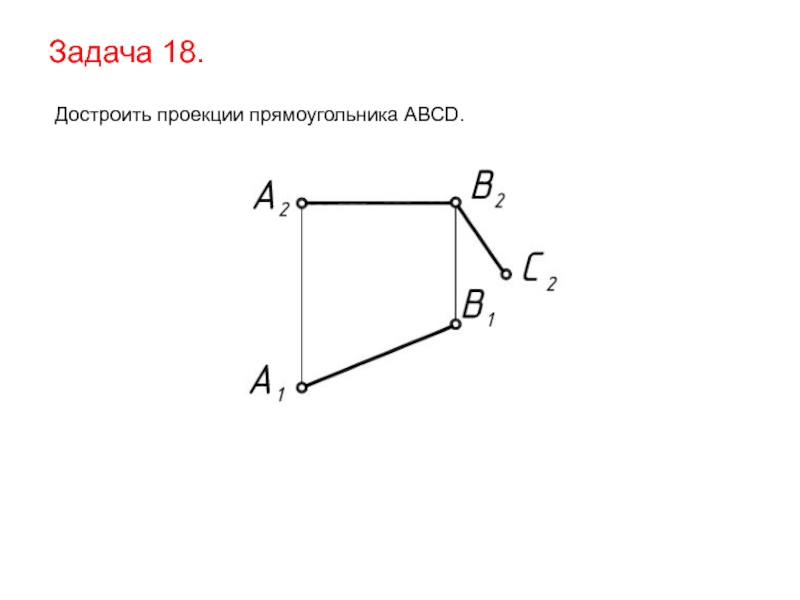
- 48. Задача 18. Достроить проекции прямоугольника АВСD.
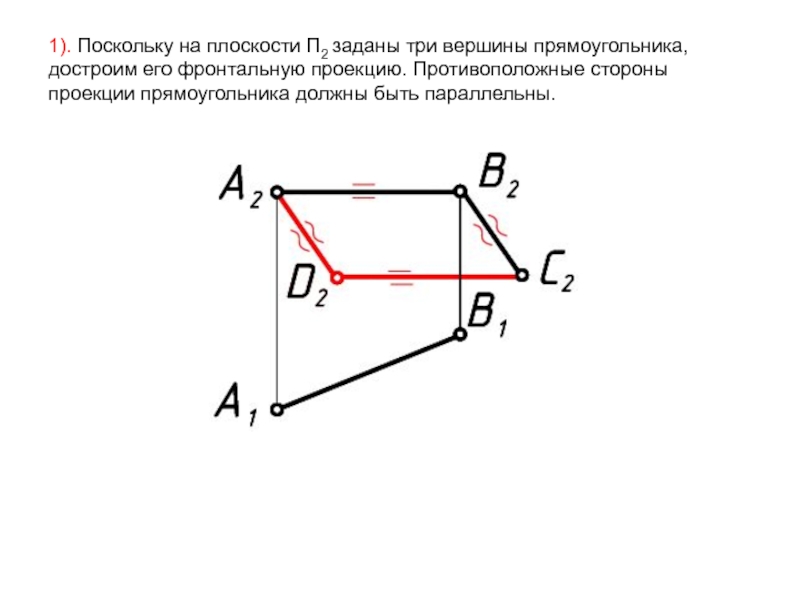
- 49. 1). Поскольку на плоскости П2 заданы три
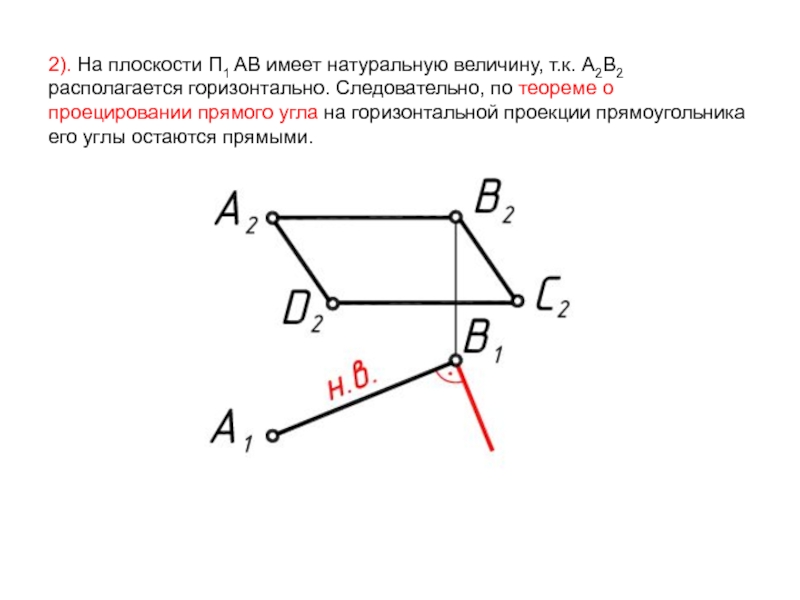
- 50. 2). На плоскости П1 АВ имеет натуральную
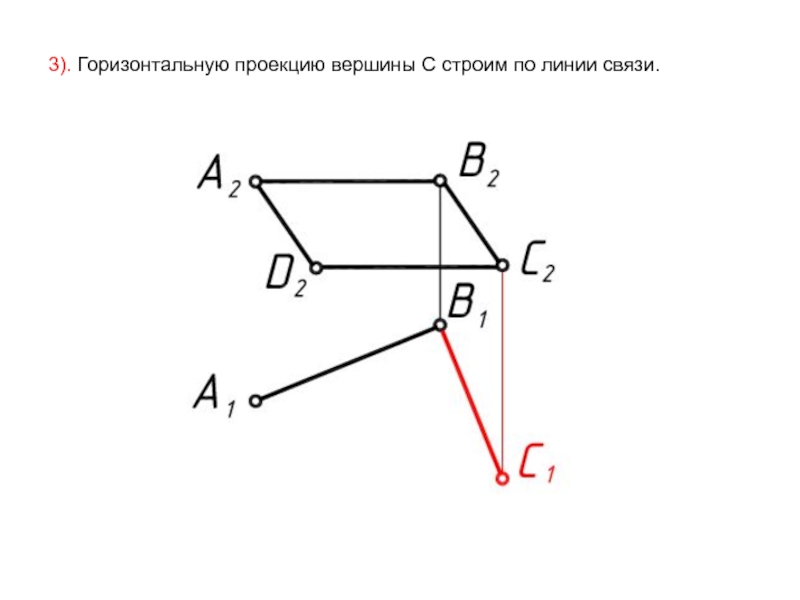
- 51. 3). Горизонтальную проекцию вершины С строим по линии связи.
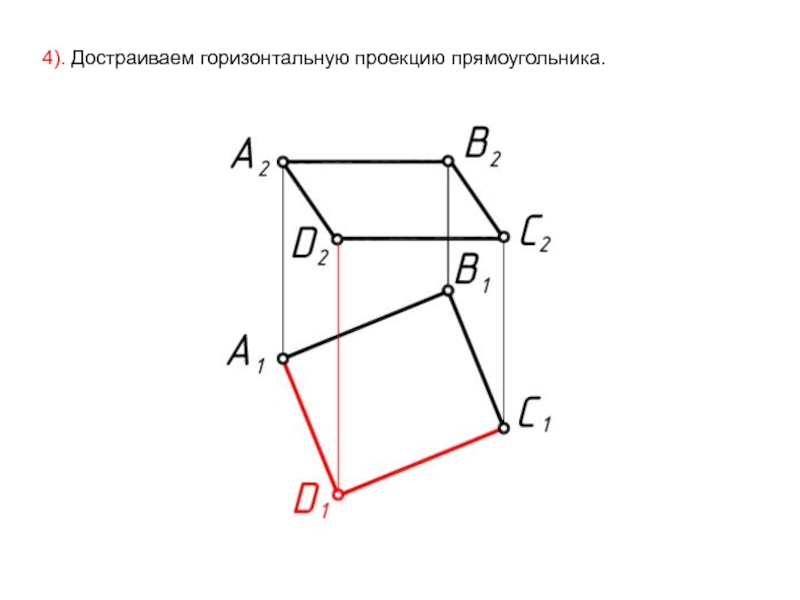
- 52. 4). Достраиваем горизонтальную проекцию прямоугольника.
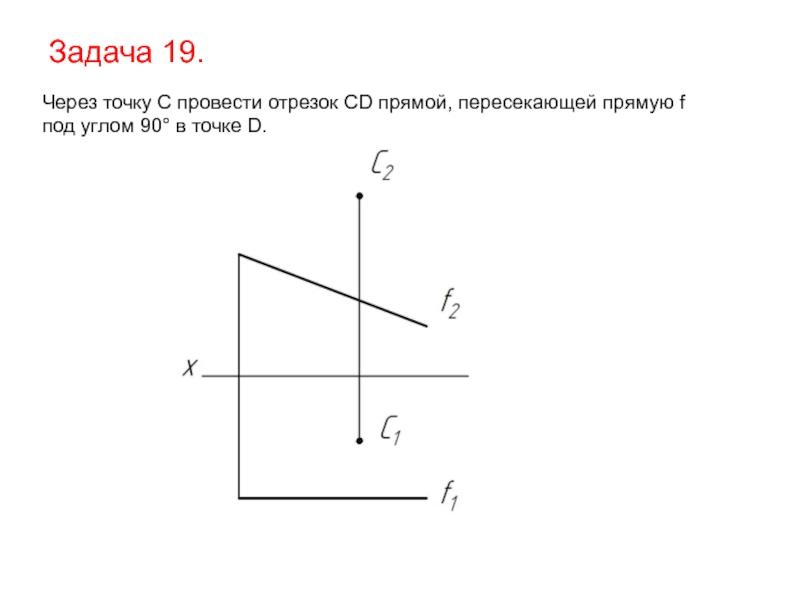
- 53. Задача 19. Через точку С провести отрезок
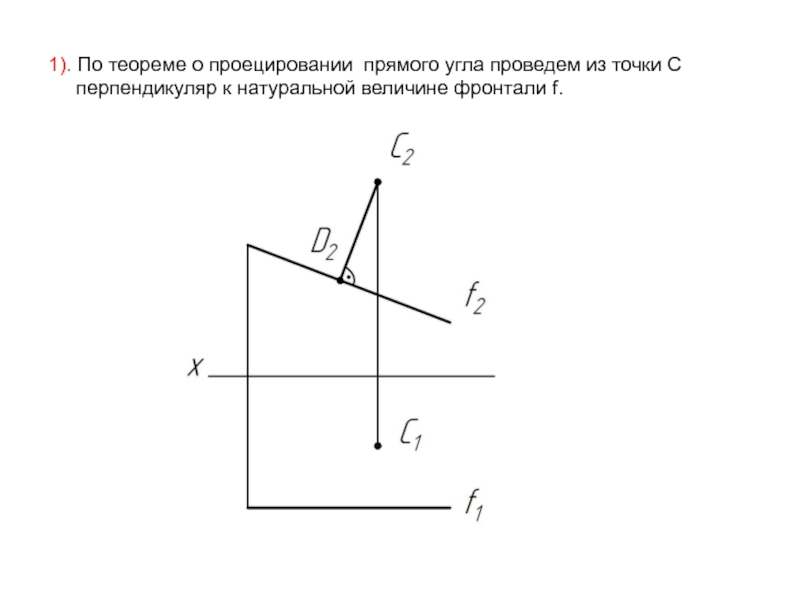
- 54. 1). По теореме о проецировании прямого угла
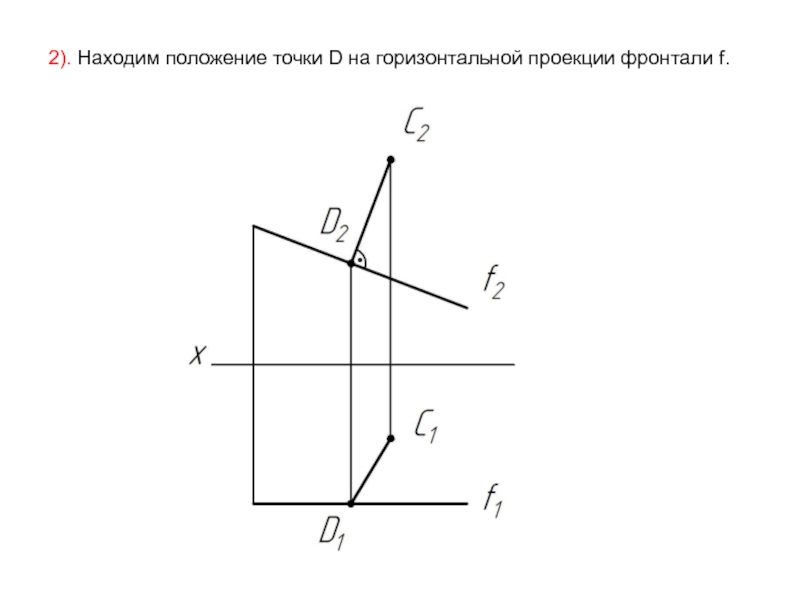
- 55. 2). Находим положение точки D на горизонтальной проекции фронтали f.
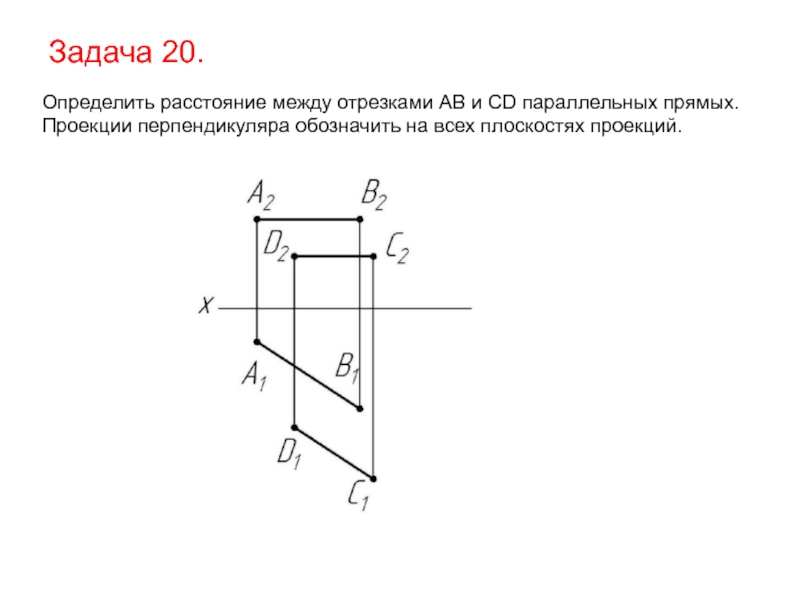
- 56. Задача 20. Определить расстояние между отрезками AB
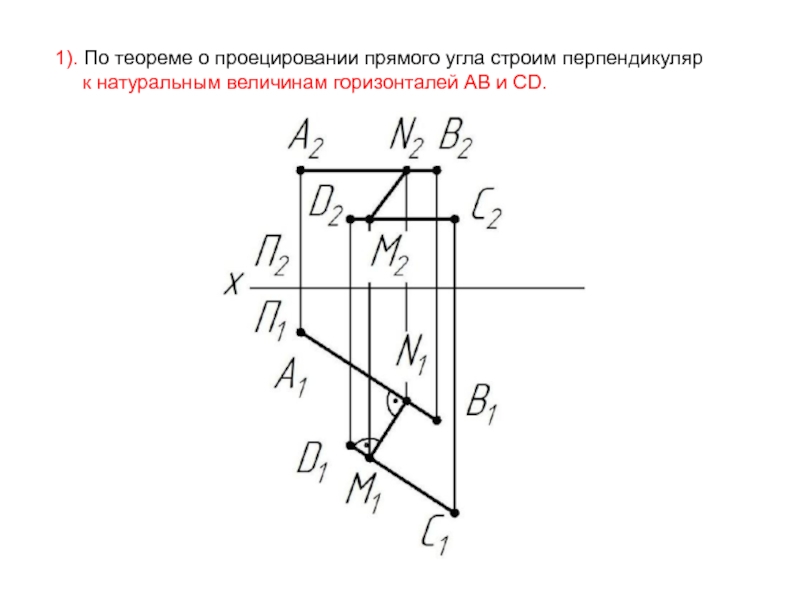
- 57. 1). По теореме о проецировании прямого угла
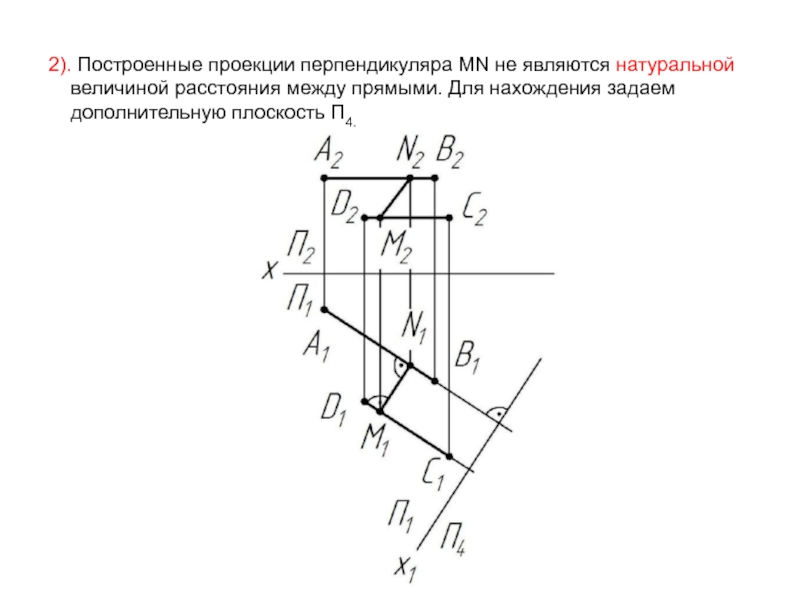
- 58. 2). Построенные проекции перпендикуляра MN не являются
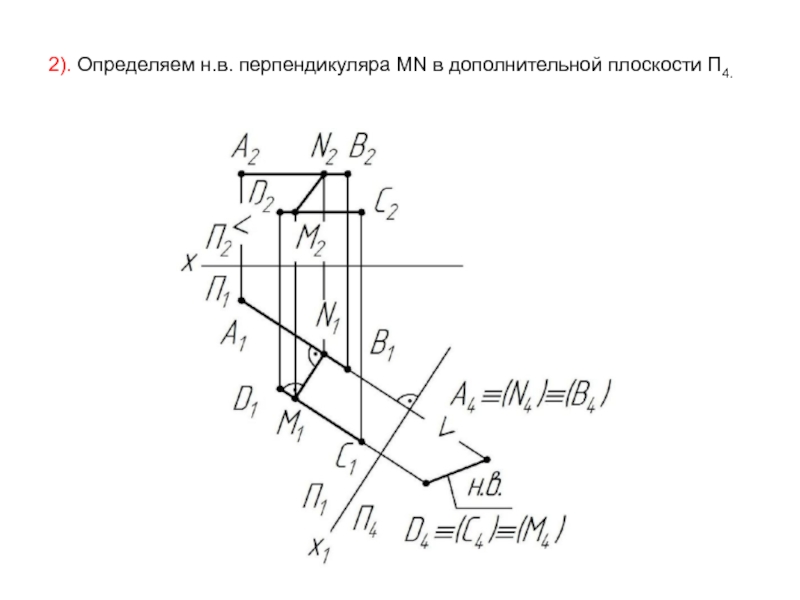
- 59. 2). Определяем н.в. перпендикуляра MN в дополнительной плоскости П4.
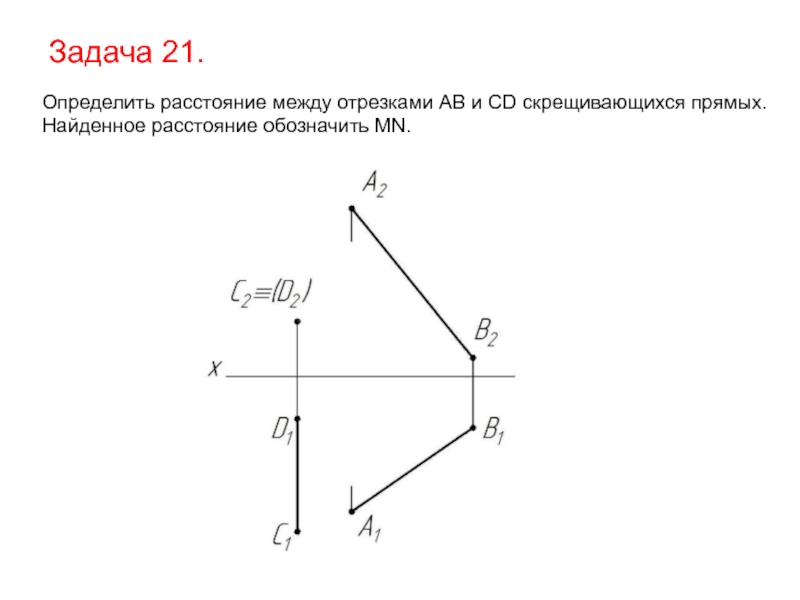
- 60. Задача 21. Определить расстояние между отрезками AB и CD скрещивающихся прямых. Найденное расстояние обозначить MN.
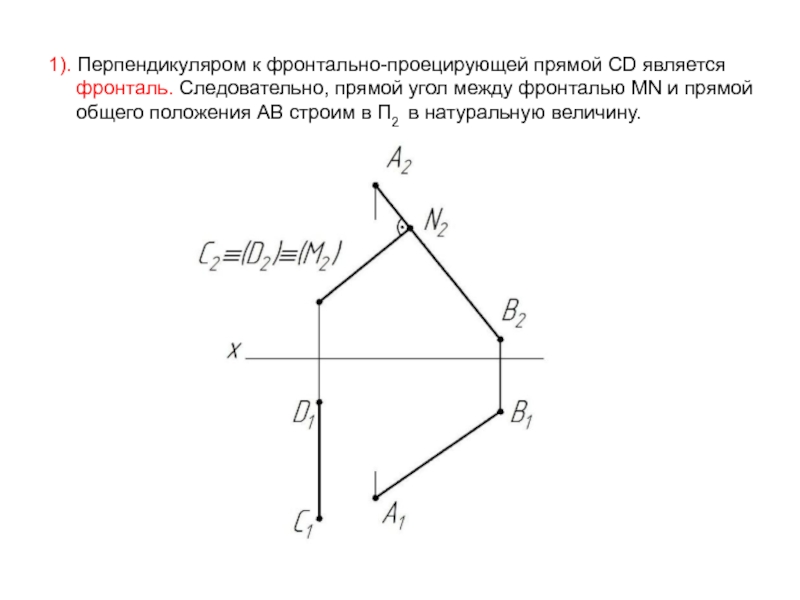
- 61. 1). Перпендикуляром к фронтально-проецирующей прямой CD является
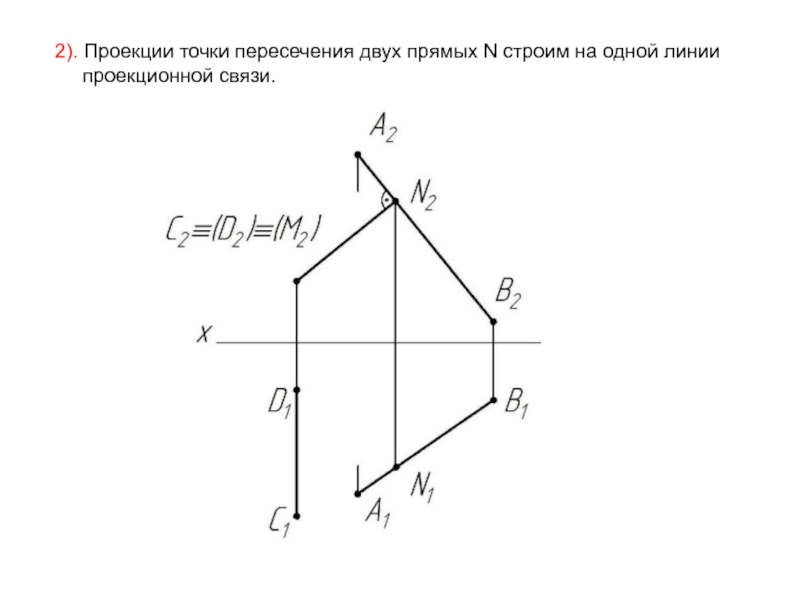
- 62. 2). Проекции точки пересечения двух прямых N
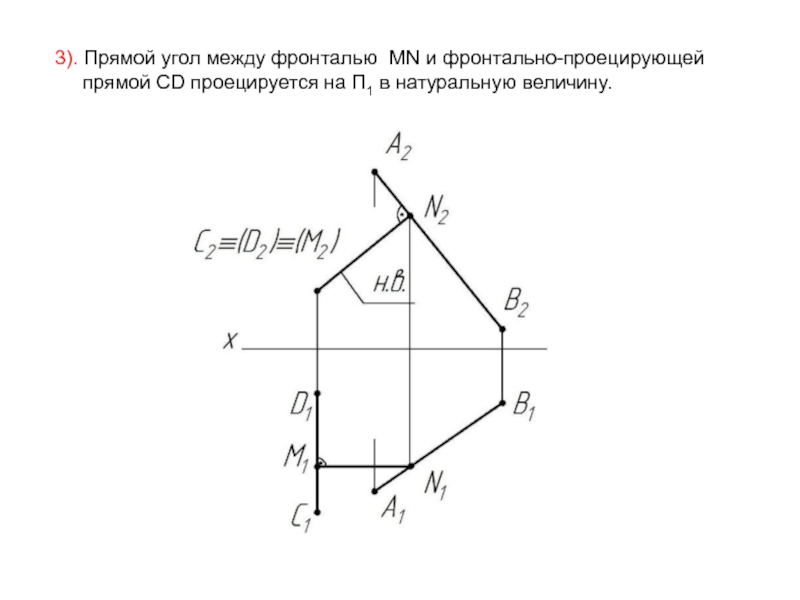
- 63. 3). Прямой угол между фронталью MN и
Построить проекции точек, расположенных: А - выше точки В на 10 мм; С - ниже точки D на 10 мм; E - перед точкой F на 15 мм; К - за
Слайд 2Построить проекции точек, расположенных: А - выше точки В на 10
мм; С - ниже точки D на 10 мм; E - перед точкой F на 15 мм; К - за точкой L на 15 мм.
Задача 5.
Слайд 31). Для точки А по сравнению с В необходимо увеличить координату
z на 10 мм на плоскости П2. На плоскости П1, где проекции точек А и В совпадают, видимой будет точка А.
Слайд 42). Для точки С по сравнению с D необходимо уменьшить координату
z на 10 мм на плоскости П2. На плоскости П1, где проекции точек C и D совпадают, видимой будет точка D
Слайд 53). Для точки E по сравнению с F необходимо увеличить координату
y на 15 мм на плоскости П1. На плоскости П2, где проекции точек E и F совпадают, видимой будет точка E.
Слайд 64). Для точки K по сравнению с L необходимо уменьшить координату
y на 15 мм на плоскости П1. На плоскости П2, где проекции точек L и K совпадают, видимой будет точка L.
Слайд 7Задача 6.
Достроить фронтальную проекцию ломаной линии, если точки А,В,С удалены от
П1 на 15 мм, а точки D,E,F - на 25 мм.
Удаление точек от плоскости П1 определяет их координату z. Каждое звено ломаной является прямой частного положения. Построение ломаной будем осуществлять позвенно и определять положение построенного отрезка. Для профильной проекции проведем луч под углом 45 градусов.
Слайд 81). Отрезок АВ имеет координату z=15 и является фронтально проецирующей прямой,
которая перпендикулярна плоскости П2.
Слайд 92). Отрезок ВС имеет координату z=15 и является горизонталью, которая параллельна
плоскости П1.
Слайд 103). Отрезок DE имеет координату z=25 и является профильно- проецирующей прямой,
которая перпендикулярна плоскости П3.
Слайд 114). Отрезок EF имеет координату z=25 и является фронтально проецирующей прямой,
которая перпендикулярна плоскости П2.
Слайд 12Задача 7.
Через точку А провести отрезок АВ горизонтальной прямой длиной 40
мм
под углом 30° к плоскости П2 .
под углом 30° к плоскости П2 .
Слайд 131). Задаем направление проекций горизонтали, используя заданные метрические
характеристики (β=30°).
Слайд 142). На горизонтальной проекции откладываем натуральную величину длины
отрезка горизонтали 40 мм. Получаем проекцию точки В1 .
Слайд 153). Построив линию проекционной связи от В1 , получаем проекцию В2
на
заданном направлении фронтальной проекции.
заданном направлении фронтальной проекции.
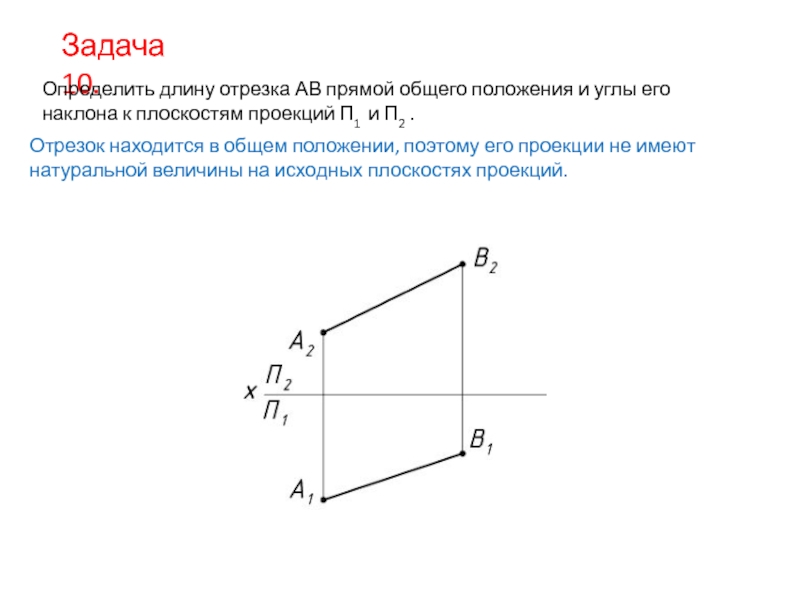
Слайд 16Задача 10.
Определить длину отрезка АВ прямой общего положения и углы его
наклона к плоскостям проекций П1 и П2 .
Отрезок находится в общем положении, поэтому его проекции не имеют натуральной величины на исходных плоскостях проекций.
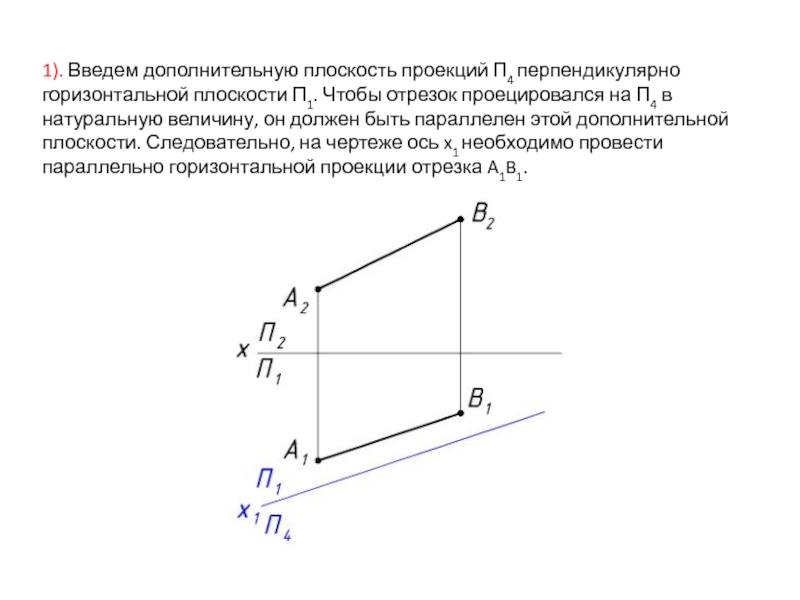
Слайд 171). Введем дополнительную плоскость проекций П4 перпендикулярно горизонтальной плоскости П1. Чтобы
отрезок проецировался на П4 в натуральную величину, он должен быть параллелен этой дополнительной плоскости. Следовательно, на чертеже ось x1 необходимо провести параллельно горизонтальной проекции отрезка A1B1.
Слайд 182). В силу ортогональности метода проецирования линии связи перпендикулярны новой оси
x1. В новой фронтальной плоскости П4 координаты z точек A и B остаются неизменными. Откладываем координаты z по линиям связи от оси x1.
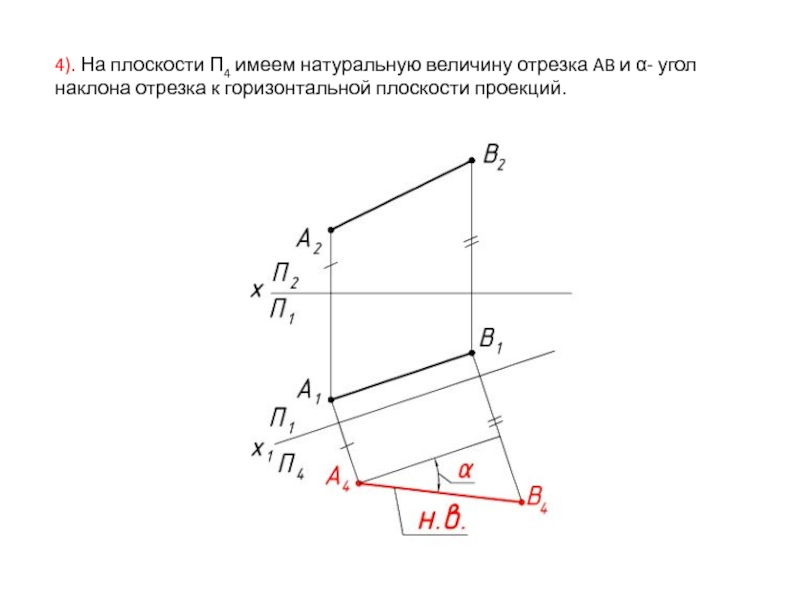
Слайд 204). На плоскости П4 имеем натуральную величину отрезка AB и α-
угол наклона отрезка к горизонтальной плоскости проекций.
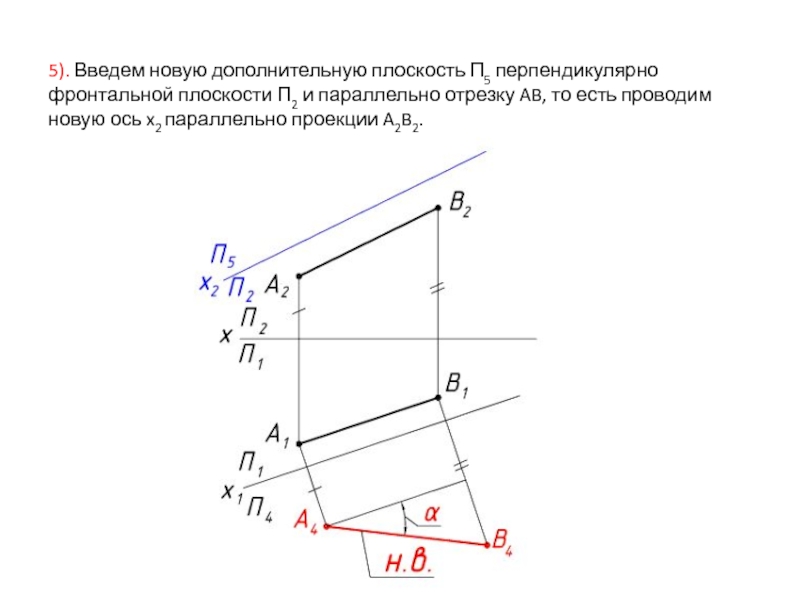
Слайд 215). Введем новую дополнительную плоскость П5 перпендикулярно фронтальной плоскости П2 и
параллельно отрезку AB, то есть проводим новую ось x2 параллельно проекции A2B2.
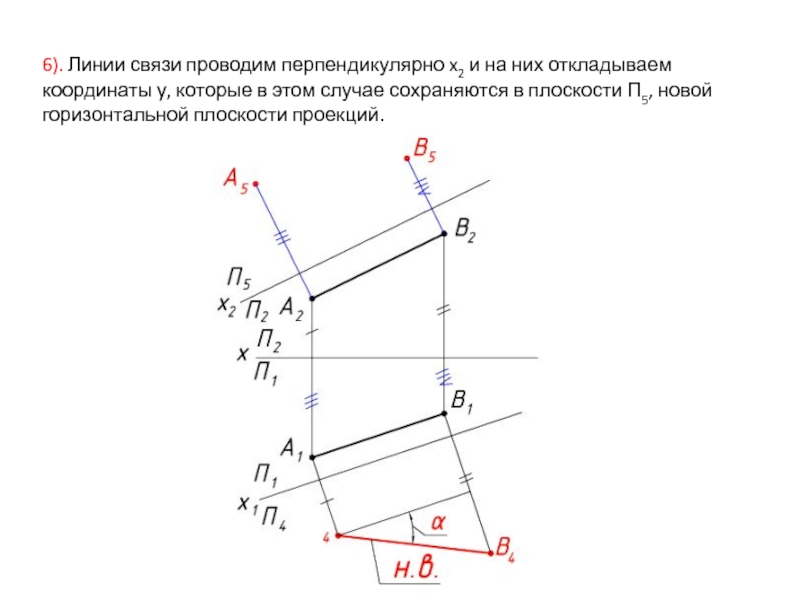
Слайд 226). Линии связи проводим перпендикулярно x2 и на них откладываем координаты
y, которые в этом случае сохраняются в плоскости П5, новой горизонтальной плоскости проекций.
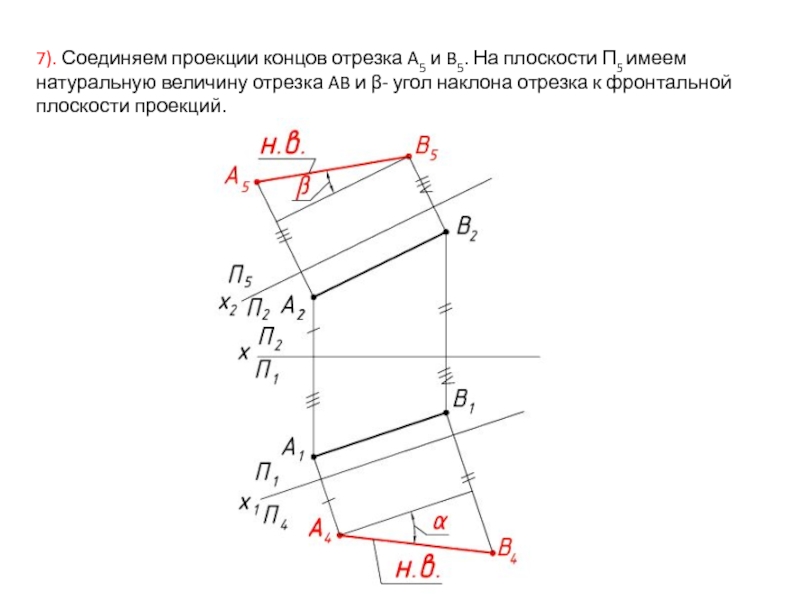
Слайд 237). Соединяем проекции концов отрезка A5 и B5. На плоскости П5
имеем натуральную величину отрезка AB и β- угол наклона отрезка к фронтальной плоскости проекций.
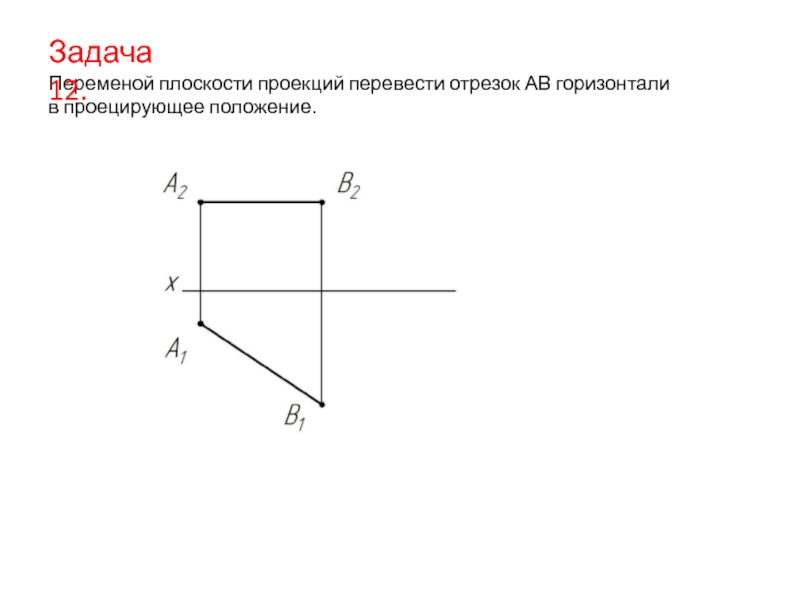
Слайд 24Переменой плоскости проекций перевести отрезок АВ горизонтали
в проецирующее положение.
Задача 12.
Слайд 251). На основании теоремы о проецировании прямого угла задаем дополнительную
плоскость перпендикулярно натуральной величине горизонтали АВ.
Слайд 27Задача13 а.
Определить натуральную величину отрезка АВ прямой общего положения:
а) вращением вокруг
горизонтально-проецирующей оси i, проходящей
через точку В.
через точку В.
Слайд 28 1). Вращаем прямую общего положения до положения прямой уровня –
фронтали. Достаточно повернуть точку А, чтобы задать новое положение
прямой АВ. Вращение точки производим в плоскости перпендикулярной оси i.
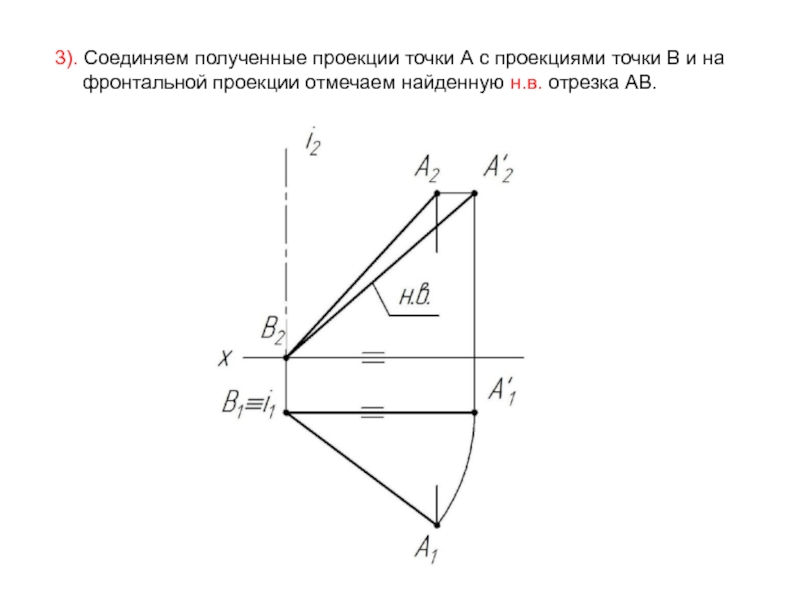
Слайд 303). Соединяем полученные проекции точки А с проекциями точки В и
на
фронтальной проекции отмечаем найденную н.в. отрезка АВ.
фронтальной проекции отмечаем найденную н.в. отрезка АВ.
Слайд 321). Построение необходимо начать с плоскости П1, т.к. горизонтальная проекция фронтали
параллельна оси x. Определим точку 1 - пересечение фронтали и прямой СD на плоскости П1.
Слайд 332). На плоскости П2 фронталь проходит через точку 1. Длина фронтали
является натуральной величиной.
Слайд 383). Проводим линию проекционной связи от полученной проекции В1 и
находим положение проекции точки В2.
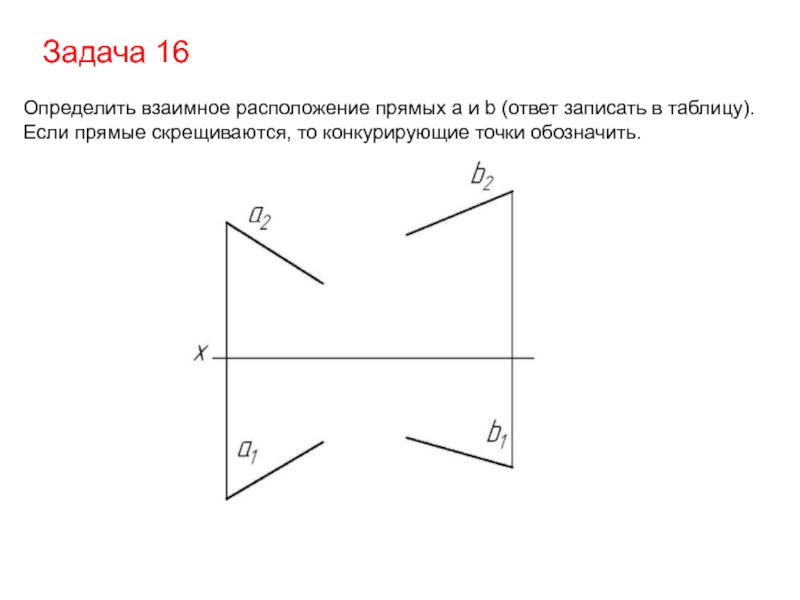
Слайд 39Задача 16
Определить взаимное расположение прямых a и b (ответ записать в
таблицу).
Если прямые скрещиваются, то конкурирующие точки обозначить.
Если прямые скрещиваются, то конкурирующие точки обозначить.
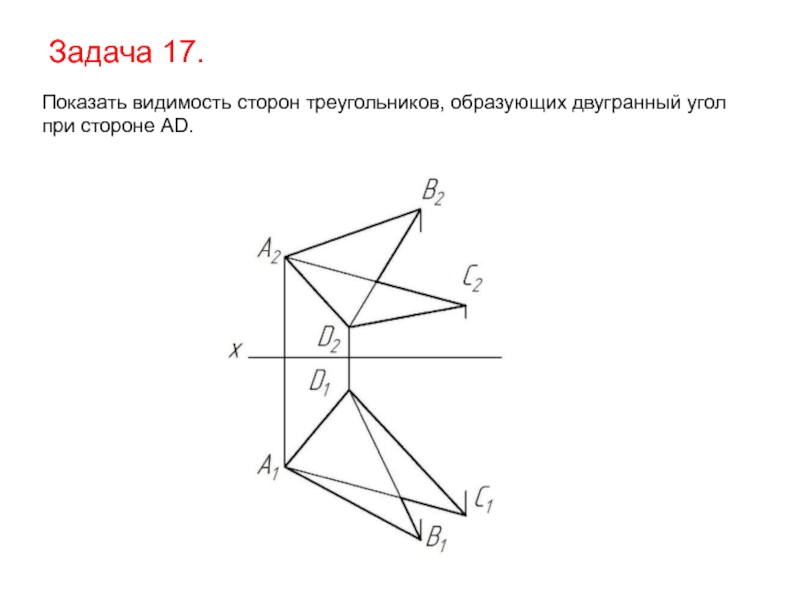
Слайд 43Задача 17.
Показать видимость сторон треугольников, образующих двугранный угол
при стороне AD.
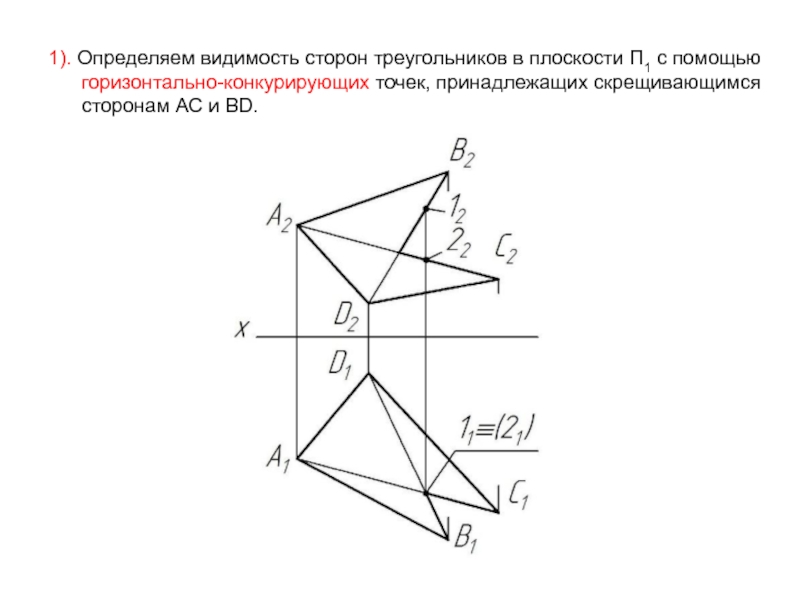
Слайд 441). Определяем видимость сторон треугольников в плоскости П1 с помощью
горизонтально-конкурирующих точек, принадлежащих скрещивающимся
сторонам AC и BD.
сторонам AC и BD.
Слайд 452). Видимость сторон треугольников AC и BD в плоскости П1 показываем
графически, изменив заданный тип линии.
Слайд 463). Определяем видимость сторон треугольников в плоскости П2 с помощью
фронтально-конкурирующих точек, принадлежащих скрещивающимся
сторонам AC и BD.
сторонам AC и BD.
Слайд 474). Видимость сторон треугольников AC и BD в плоскости П2 показываем
графически, изменив заданный тип линии.
Слайд 491). Поскольку на плоскости П2 заданы три вершины прямоугольника, достроим его
фронтальную проекцию. Противоположные стороны проекции прямоугольника должны быть параллельны.
Слайд 502). На плоскости П1 АВ имеет натуральную величину, т.к. А2В2 располагается
горизонтально. Следовательно, по теореме о проецировании прямого угла на горизонтальной проекции прямоугольника его углы остаются прямыми.
Слайд 53Задача 19.
Через точку С провести отрезок CD прямой, пересекающей прямую f
под
углом 90° в точке D.
Слайд 541). По теореме о проецировании прямого угла проведем из точки C
перпендикуляр к натуральной величине фронтали f.
Слайд 56Задача 20.
Определить расстояние между отрезками AB и CD параллельных прямых.
Проекции перпендикуляра
обозначить на всех плоскостях проекций.
Слайд 571). По теореме о проецировании прямого угла строим перпендикуляр
к натуральным величинам горизонталей AB и CD.
Слайд 582). Построенные проекции перпендикуляра MN не являются натуральной
величиной расстояния
между прямыми. Для нахождения задаем
дополнительную плоскость П4.
дополнительную плоскость П4.
Слайд 60Задача 21.
Определить расстояние между отрезками AB и CD скрещивающихся прямых.
Найденное расстояние
обозначить MN.
Слайд 611). Перпендикуляром к фронтально-проецирующей прямой CD является
фронталь. Следовательно,
прямой угол между фронталью MN и прямой
общего положения AB строим в П2 в натуральную величину.
общего положения AB строим в П2 в натуральную величину.
Слайд 633). Прямой угол между фронталью MN и фронтально-проецирующей
прямой CD проецируется на П1 в натуральную величину.
