- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на движение. Математические модели презентация
Содержание
- 1. Задачи на движение. Математические модели
- 2. 1. Путь от
- 3. 1. Путь от
- 4. 2. Дорога из
- 5. 16у+15х+16z=180 x+у+z=11,5 x+у+z=11,5
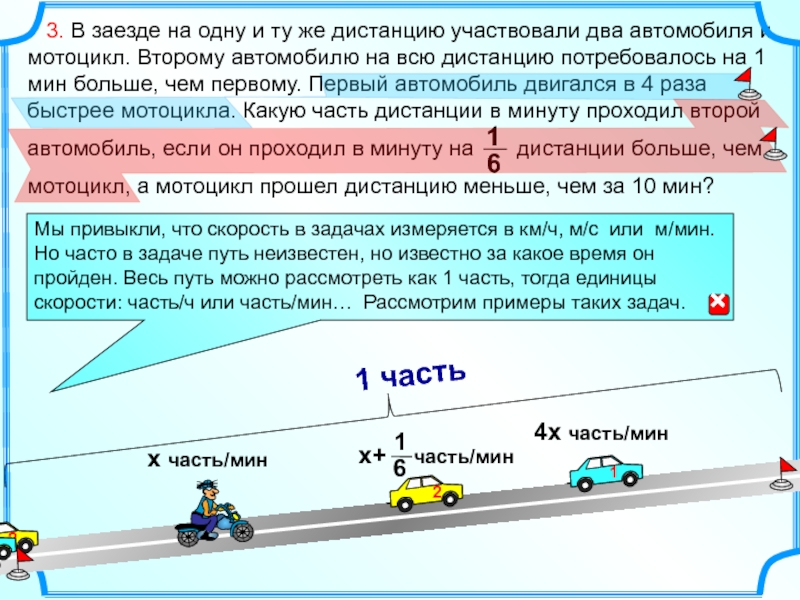
- 6. х часть/мин 4х часть/мин
- 7. на 1 мин > = 1 –
- 8. 18х – 1 = 24х2 + 4х
- 9. 4х х х+1 2 способ
- 10. 4. На соревнованиях
- 11. 4. На соревнованиях по
- 12. 5. По двум концентрическим
- 13. 2 случай 5. По
- 14. 6. Два спортсмена
- 15. 6. Два спортсмена бегут
- 16. Задачи для самостоятельной работы. 1.
- 17. Форма для поверки ответов.
Слайд 2
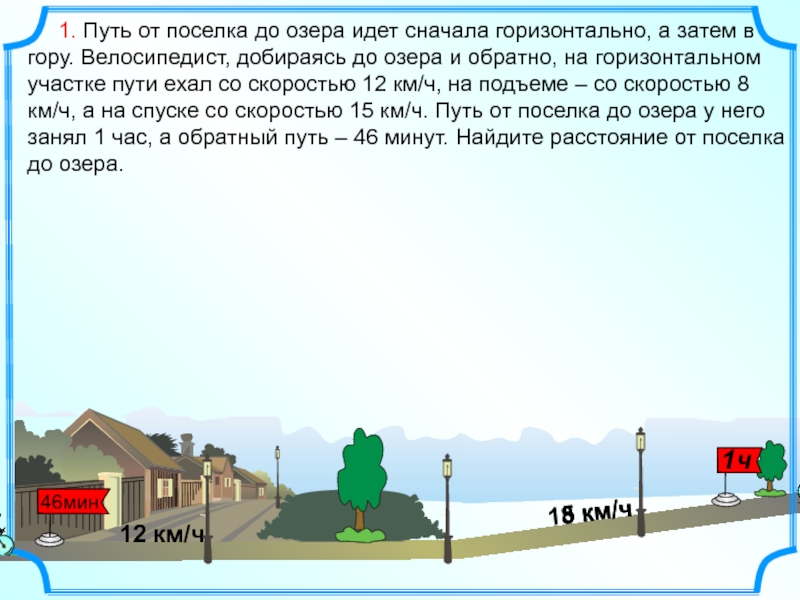
1. Путь от поселка до озера идет сначала
12 км/ч
8 км/ч
15 км/ч
Слайд 3
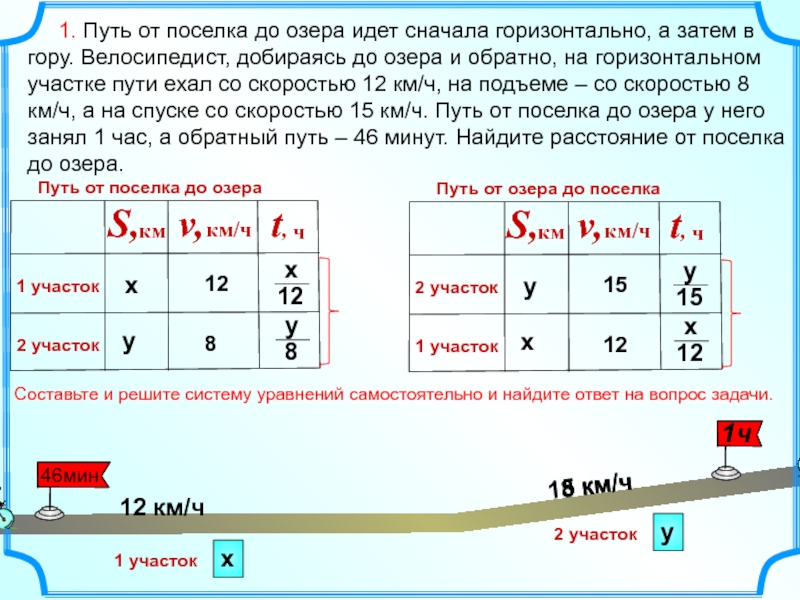
1. Путь от поселка до озера идет сначала
12 км/ч
8 км/ч
15 км/ч
Путь от поселка до озера
Путь от озера до поселка
1 участок
2 участок
Составьте и решите систему уравнений самостоятельно и найдите ответ на вопрос задачи.
Слайд 4
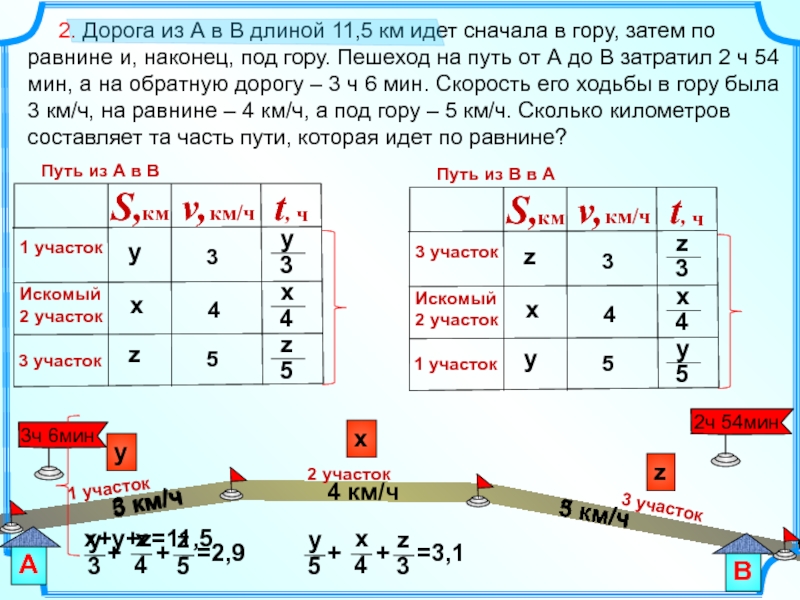
2. Дорога из А в В длиной 11,5
3 км/ч
5 км/ч
4 км/ч
1 участок
2 участок
3 участок
3 км/ч
5 км/ч
x+у+z=11,5
Слайд 516у+15х+16z=180
x+у+z=11,5
x+у+z=11,5
11,5–х
х= 4
– х= – 4
Значения у и
Ответ: длина горизонтального участка 4 км.
Слайд 818х – 1 = 24х2 + 4х
24х2 – 14х +1 =
D/4 = (-7)2 – 24 = 25
а = 24, k = -7, c = 1
Перейдем к целым числам
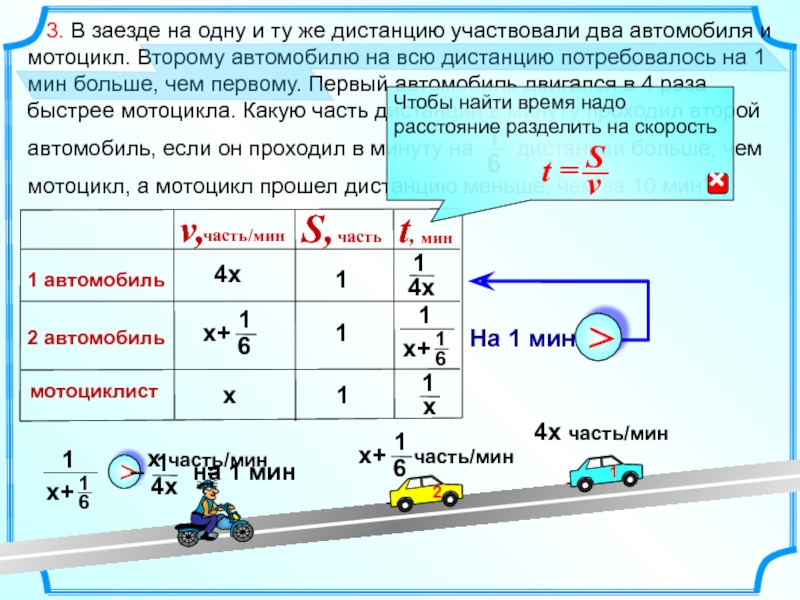
Ответим на вопрос задачи: какую часть дистанции в минуту проходил 2 автомобиль
«мотоцикл прошел дистанцию меньше, чем за 10 мин»
Проверим, оба ли корня удовлетворяют условию задачи, может
среди них есть посторонний корень? Найдем время мотоциклиста…
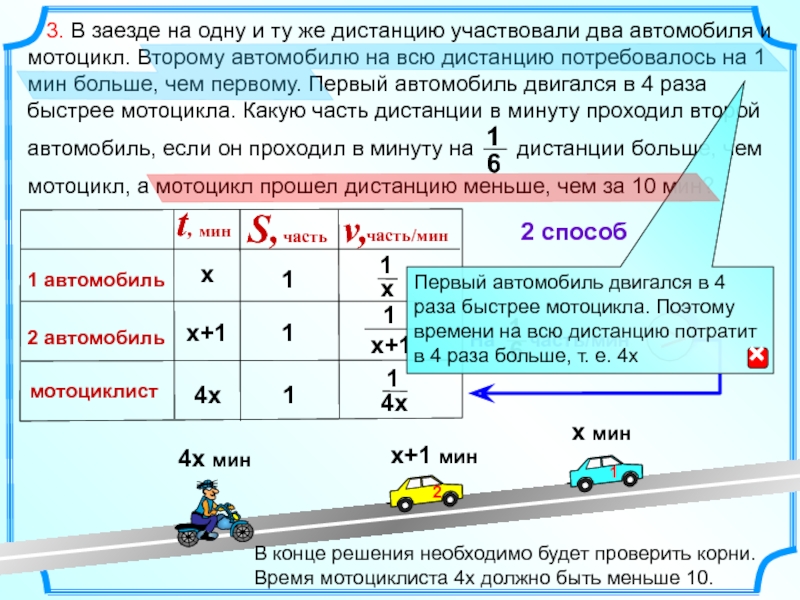
Слайд 94х
х
х+1
2 способ
В конце решения необходимо будет проверить корни.
Время мотоциклиста
Слайд 10
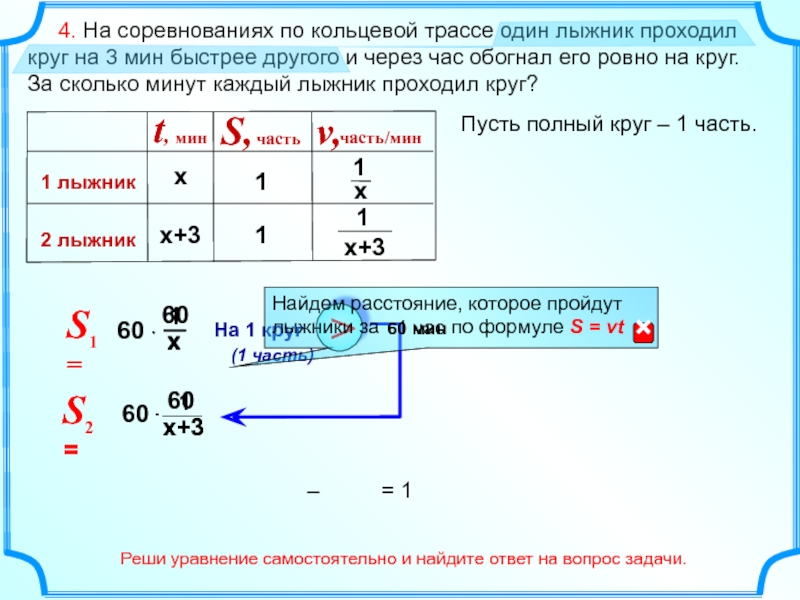
4. На соревнованиях по кольцевой трассе один лыжник
Пусть полный круг – 1 часть.
Слайд 11 4. На соревнованиях по кольцевой трассе один лыжник
Пусть полный круг – 1 часть.
х
х+3
60
S1=
S2 =
1
60
Найдем расстояние, которое пройдут
лыжники за по формуле S = vt
– = 1
1 час
60 мин
Реши уравнение самостоятельно и найдите ответ на вопрос задачи.
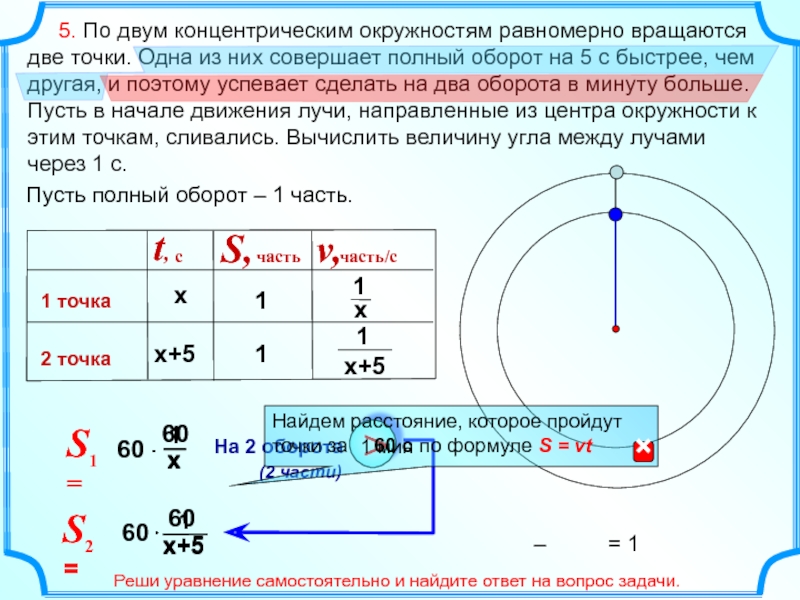
Слайд 12 5. По двум концентрическим окружностям равномерно вращаются две
Пусть полный оборот – 1 часть.
х
х+5
60
S1=
S2 =
1
60
Найдем расстояние, которое пройдут
точки за по формуле S = vt
– = 1
1 мин
60 с
Реши уравнение самостоятельно и найдите ответ на вопрос задачи.
Слайд 132 случай
5. По двум концентрическим окружностям равномерно вращаются
Подсказки.
Решив уравнение вы еще не получите ответ на вопрос задачи. За х мы обозначили время, за которое пройдет 1-я точка полный круг.
Еще придется найти скорость, причем скорость будет в необычных единицах – часть/с.
Часть от полного круга, а полный круг 3600.
Еще подсказка: в условии задачи не указано как именно двигались точки. Значит, они могли двигаться в одном направлении, а может и в противоположных, т.е. задача будет иметь два решения.
1 случай
Слайд 14
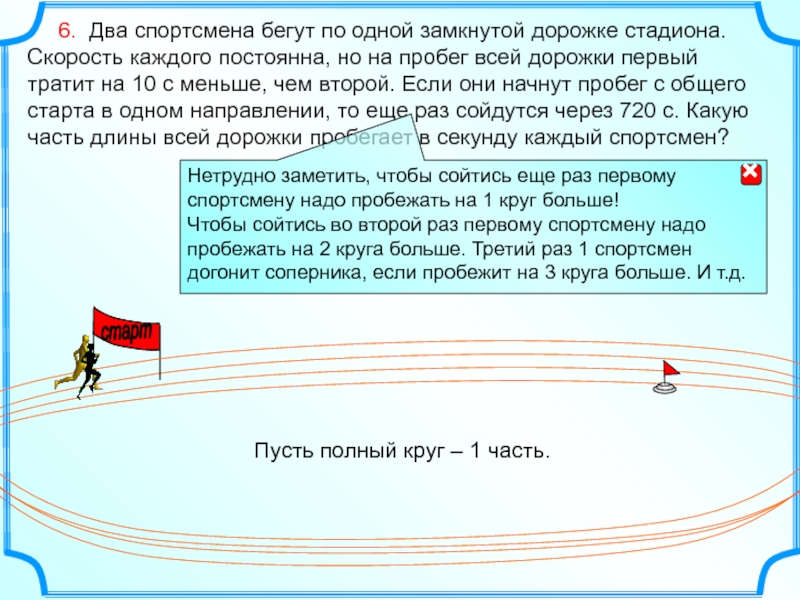
6. Два спортсмена бегут по одной замкнутой дорожке
Пусть полный круг – 1 часть.
Слайд 15 6. Два спортсмена бегут по одной замкнутой дорожке
Пусть полный круг – 1 часть.
х
х+10
720
S1=
S2 =
1
720
Найдем расстояние, которое пробегут
спортсмены за 720с по формуле S = vt
– = 1
Реши уравнение самостоятельно и найдите ответ на вопрос задачи.
Слайд 16Задачи для самостоятельной работы.
1.
От почты А до поселка В надо пройти
2.
Дорога от поселка до станции идет сначала в гору, а потом под гору, при этом ее длина равна 9 км. Пешеход на подъеме идет со скоростью, на 2 км/ч меньшей, чем на спуске. Путь от поселка до станции занимает у него 1 ч 50 мин, а обратный путь занимает 1 ч 55 мин. Определите длину подъема на пути к станции и скорости пешехода на подъеме и спуске.
3.
На тренировке по картингу один карт проходил круг на 10 сек медленнее другого и через минуту отстал от него ровно на круг. За сколько секунд каждый карт проходил круг?
Слайд 17
Форма для поверки ответов.
max 15
Задача 1.
Задача
Задача 5.
Задача 1.
Задача 2.
Уравнения
Задачи для самостоятельной работы
км
км/ч, 2 лыжник
(0)
км
км/ч, скорость на спуске
км/ч
1 лыжник
Если точки движутся в одном направлении
Если точки движутся в противоположных направлениях
(0)
км,
Длина подъема
Задача 3.
с
с, 2 спортсмен
1 спортсмен
Задача 6.
часть/с, 2 спортсмен
1 спортсмен
часть/с
скорость на подъеме
км/ч