- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача двух тел. Уравнения движения в задаче двух тел презентация
Содержание
- 1. Задача двух тел. Уравнения движения в задаче двух тел
- 2. Уравнения движения в задаче двух тел Движение
- 3. Массы m1 и m2 притягивают друг друга
- 4. Уравнения движения тела m2, притягиваемого телом m1 будут иметь вид (1)
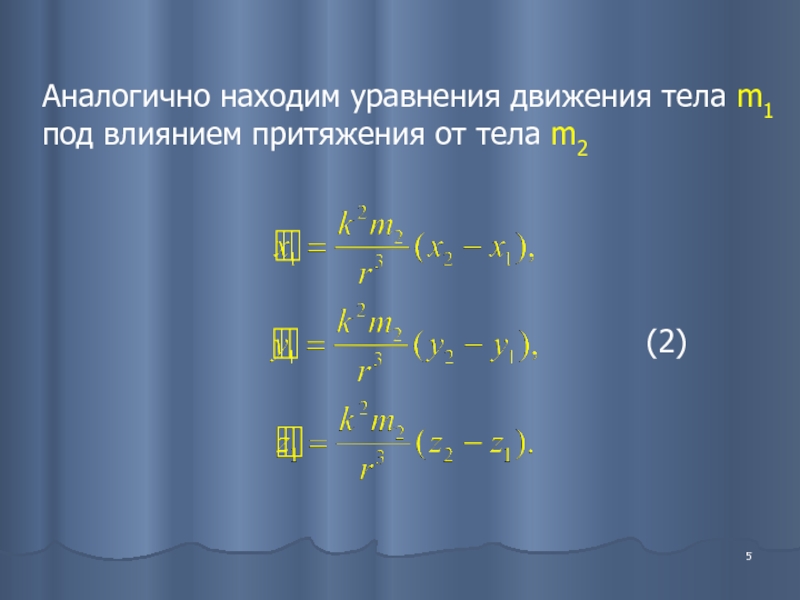
- 5. Аналогично находим уравнения движения тела m1 под влиянием притяжения от тела m2 (2)
- 6. Вычитая из (1) уравнения (2) находим уравнения движения тела m2 относительно m1
- 7. Вводя обозначения и окончательно получим (3)
- 8. Интегралы площадей Умножаем первое уравнение системы (3)
- 9. Интегралы площадей В итоге получим: Интегрируя эти соотношения, находим (4)
- 10. Домножаем равенства (4) на z, x, y соответственно и складываем (5) получим:
- 11. Это уравнение плоскости, проходящей через начало координат.
- 12. Обозначим через ΔА – площадь треугольника OPQ,
- 13. Перепишем последнее равенство в виде: При отношение
- 14. Посмотрим теперь как будет выглядеть последнее выражение в прямоугольных координатах: Отсюда: В итоге находим: (!!!)
- 15. Постоянные а1, а2, а3 – проекции удвоенной
- 16. Ω – долгота восходящего узла, отсчитывается
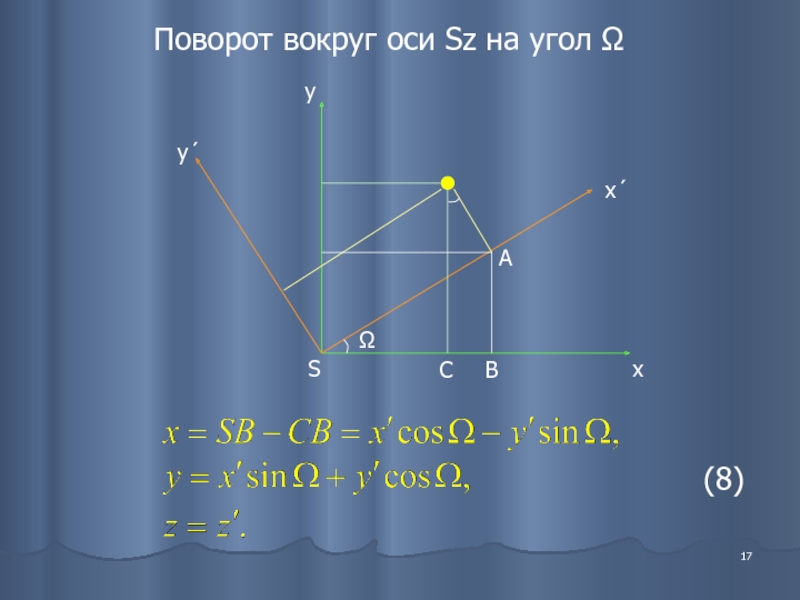
- 17. Поворот вокруг оси Sz на угол Ω (8)
- 18. В матричной форме этот поворот можно записать следующим образом: (9)
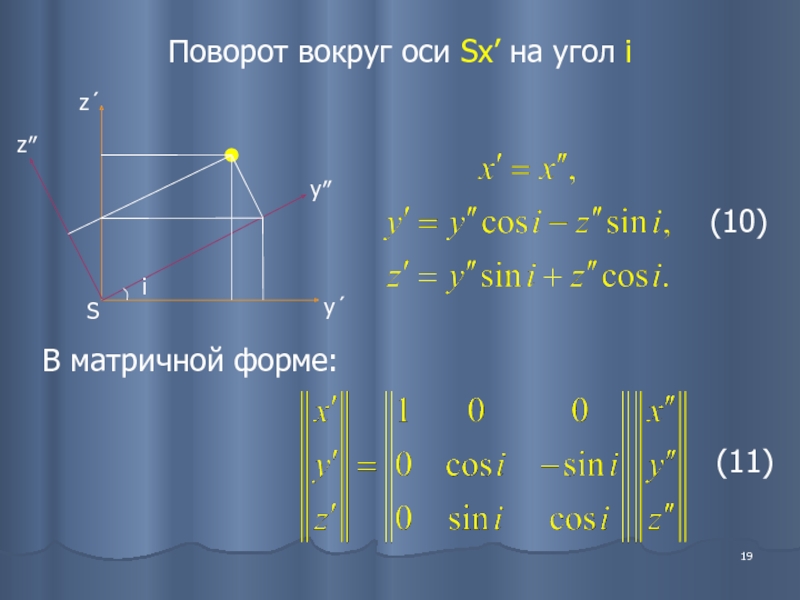
- 19. Поворот вокруг оси Sx’ на угол i В матричной форме: (10) (11)
- 20. Таким образом, после двух поворотов, имеем: Перемножив поворотные матрицы получим: (12)
- 21. Так как компоненты удвоенной секториальной скорости в
- 22. Перепишем теперь интегралы площадей: (14) Осталось связать
- 23. Умножим первое, второе и третье уравнения системы (3) на Сложив, получим:
- 24. можно переписать в виде: Правую – в виде: Левую часть равенства
- 25. Таким образом, имеем: Интегрирование последнего выражения дает
- 26. Так как движение происходит в плоскости, то
- 27. Перейдем теперь от прямоугольных координат x″, y″
- 28. Из равенств (16) и (17) имеем Таким образом При помощи (16) можно найти (18)
- 29. Уравнение (18) можно переписать в виде: Преобразуем подкоренное выражение: Обозначим:
- 30. Имеем: Далее Введем замену Получим: или
- 31. Последнее выражение можно проинтегрировать где ω – постоянная интегрирования. Отсюда Но Поэтому
- 32. или Отсюда Сравнивая теперь со стандартным уравнением
- 33. находим: Здесь ω – аргумент перицентра (угловое
- 34. С этими постоянными интеграл энергии Уравнение траектории (19) (20) (21) Уравнение интеграла площадей:
- 35. Введем для случая эллиптического движения некоторую вспомогательную
- 36. Отношение малой и большой полуоси будет: Здесь
- 37. x2/a2+y2/b2=1 – уравнение эллипса x'2/a2+y'2/a2=1 – уравнение окружности x=x' y=MN y‘=M‘N
- 38. Подставляя (24) в (22) и (23), получим
- 39. Делим первое на второе: Используя тригонометрические соотношения окончательно находим: (26) (25’)
- 40. Найдем теперь уравнение, связывающее переменную E со временем. Дифференцируя соотношение (26) получим: Отсюда
- 41. Из интеграла площадей (21) Учитывая, что Имеем
- 42. Используя также выражение для радиус-вектора (24) Откуда имеем и второе из соотношений (25’) находим:
- 43. Интегрируя, находим: (27) Здесь – постоянная интегрирования
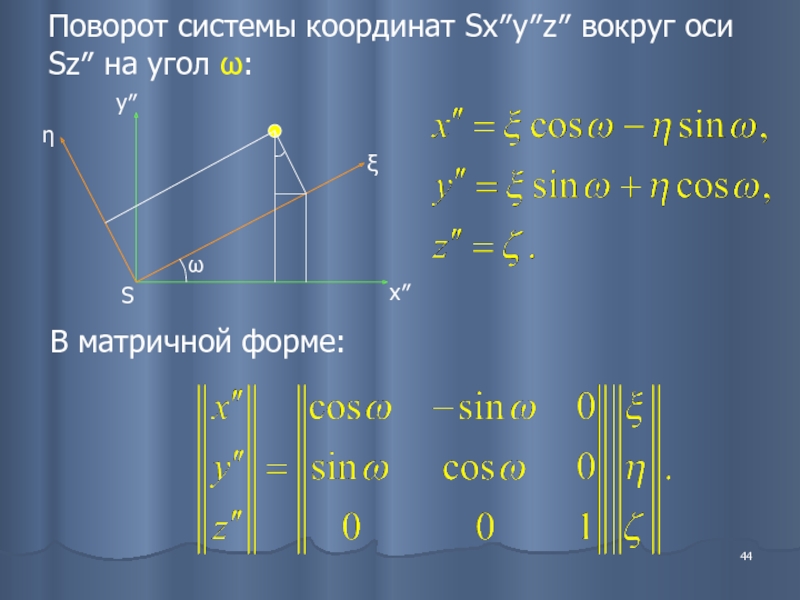
- 44. Поворот системы координат Sx″y″z″ вокруг оси Sz″ на угол ω: В матричной форме:
- 45. Таким образом, получить выражения для координат x,
- 46. Так как движение в задаче двух тел
- 47. Уравнение Кеплера, связывающее эксцентрическую аномалию и время,
- 48. Формулы, связывающие координаты x, y, z с элементами орбиты
- 49. Формулы для скоростей находим дифференцированием формул для координат
- 50. Формулы для координат и скоростей представляют также в виде Проективные коэффициенты
Уравнения движения
в задаче двух тел Движение двух материальных точек будем рассматривать в инерциальной системе отсчета.
Слайд 2Уравнения движения
в задаче двух тел
Движение двух материальных точек будем рассматривать в
инерциальной системе отсчета.
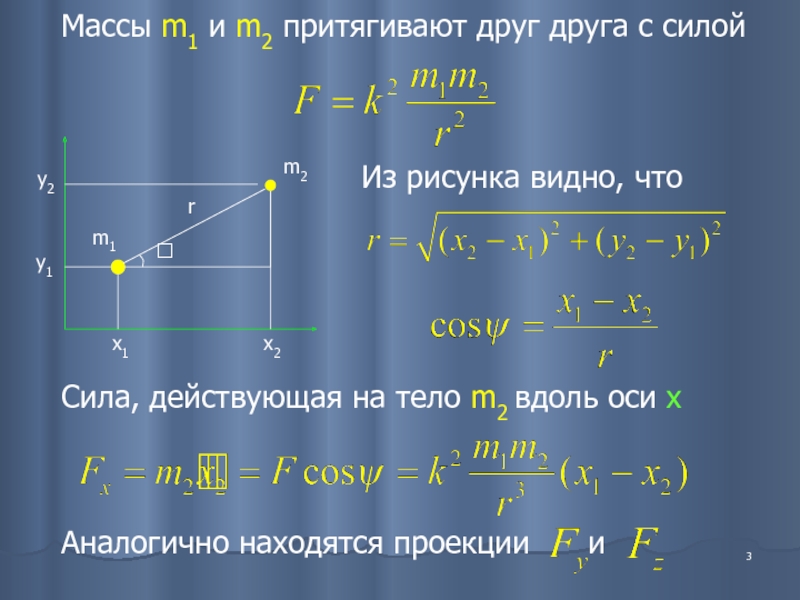
Слайд 3Массы m1 и m2 притягивают друг друга с силой
Сила, действующая на
тело m2 вдоль оси x
Из рисунка видно, что
Аналогично находятся проекции
и
Слайд 8Интегралы площадей
Умножаем первое уравнение системы (3) на –y, второе – на
x, и складываем их. Затем складываем второе, умноженное на –z, с третьим, умноженным на y и первое, умноженное на z с третьим, умноженным на –x.
Слайд 11Это уравнение плоскости, проходящей через начало координат. В этой плоскости происходит
движение тела m2.
Постоянные а1, а2, а3 определяют положение плоскости орбиты этого тела относительно осей координат. Смысл этих постоянных можно усмотреть из следующего рисунка.
Постоянные а1, а2, а3 определяют положение плоскости орбиты этого тела относительно осей координат. Смысл этих постоянных можно усмотреть из следующего рисунка.
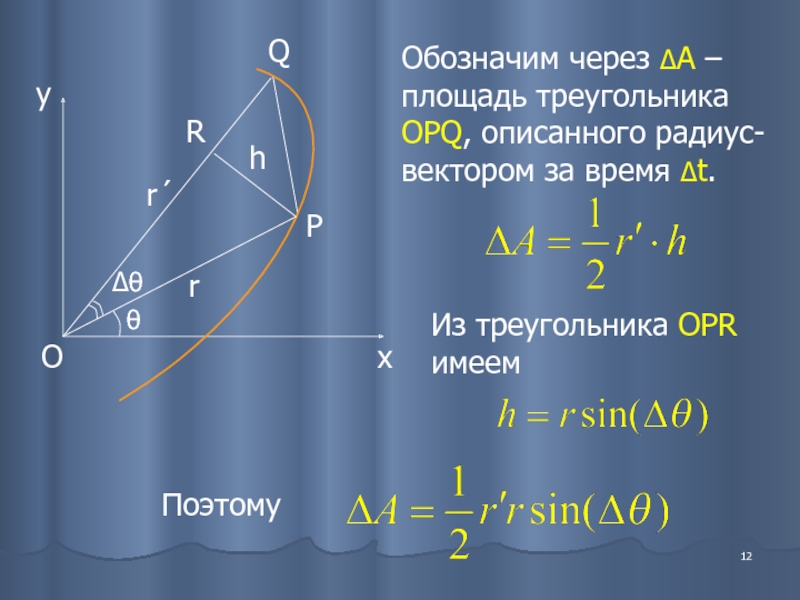
Слайд 12Обозначим через ΔА – площадь треугольника OPQ, описанного радиус-вектором за время
Δt.
Из треугольника OPR имеем
Поэтому
Слайд 13Перепишем последнее равенство в виде:
При
отношение площади треугольника
к площади сектора
,
В пределе при
имеем:
Это
секториальная скорость движущейся точки.
(6)
Слайд 14Посмотрим теперь как будет выглядеть последнее выражение в прямоугольных координатах:
Отсюда:
В итоге
находим:
(!!!)
Слайд 15Постоянные а1, а2, а3 – проекции удвоенной секториальной скорости на плоскости
xy, yz и zx! Поэтому удвоенная секториальная скорость в плоскости орбиты будет:
При решении астрономических задач положение в пространстве плоскости орбиты принято определять не коэффициентами ее уравнения, а двумя углами Ω и i, имеющими смысл, усматриваемый из следующего рисунка:
(7)
Слайд 16
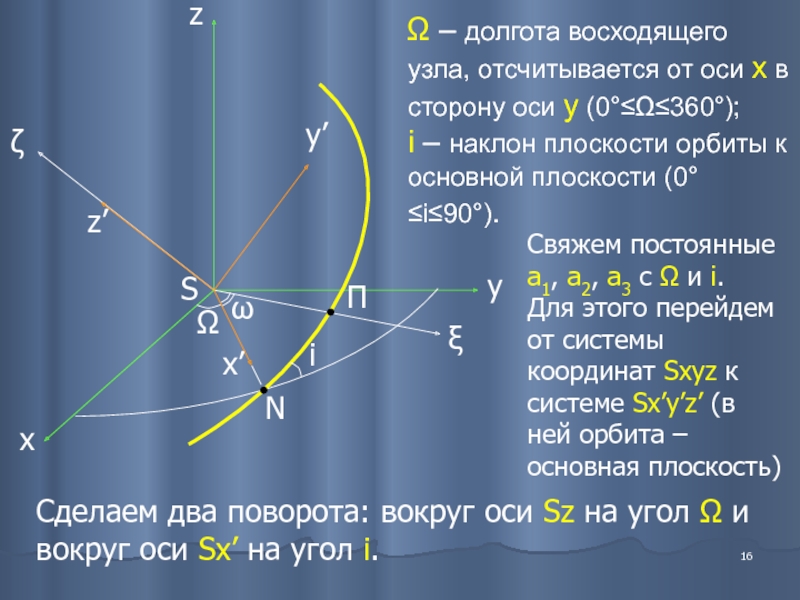
Ω – долгота восходящего узла, отсчитывается от оси x в сторону
оси y (0°≤Ω≤360°);
i – наклон плоскости орбиты к основной плоскости (0°≤i≤90°).
i – наклон плоскости орбиты к основной плоскости (0°≤i≤90°).
Свяжем постоянные а1, а2, а3 с Ω и i.
Для этого перейдем от системы координат Sxyz к системе Sx’y’z’ (в ней орбита – основная плоскость)
Сделаем два поворота: вокруг оси Sz на угол Ω и вокруг оси Sx’ на угол i.
Слайд 21Так как компоненты удвоенной секториальной скорости в системе координат Oxyz есть
а1, а2, а3, а в плоскости орбиты – 0, 0, с, то они связаны друг с другом при помощи последнего соотношения:
Отсюда:
(13)
Слайд 22Перепишем теперь интегралы площадей:
(14)
Осталось связать здесь с элементами орбиты постоянную c.
Для этого найдем сначала из уравнений движения (3) интеграл живых сил (интеграл энергии).
Слайд 25Таким образом, имеем:
Интегрирование последнего выражения дает нам интеграл энергии:
(15)
Здесь
– постоянная интеграла
энергии.
Слайд 26Так как движение происходит в плоскости, то координата z″=0, а радиус-вектор
Интеграл
площадей и интеграл живых сил в плоскости орбиты будут иметь вид
Слайд 27Перейдем теперь от прямоугольных координат x″, y″ к полярным координатам r,
u
Интеграл площадей и интеграл живых сил в полярных координатах будут иметь вид
(16)
(17)
Слайд 32или
Отсюда
Сравнивая теперь со стандартным уравнением конического сечения
где
– параметр орбиты
– большая полуось
–
эксцентриситет
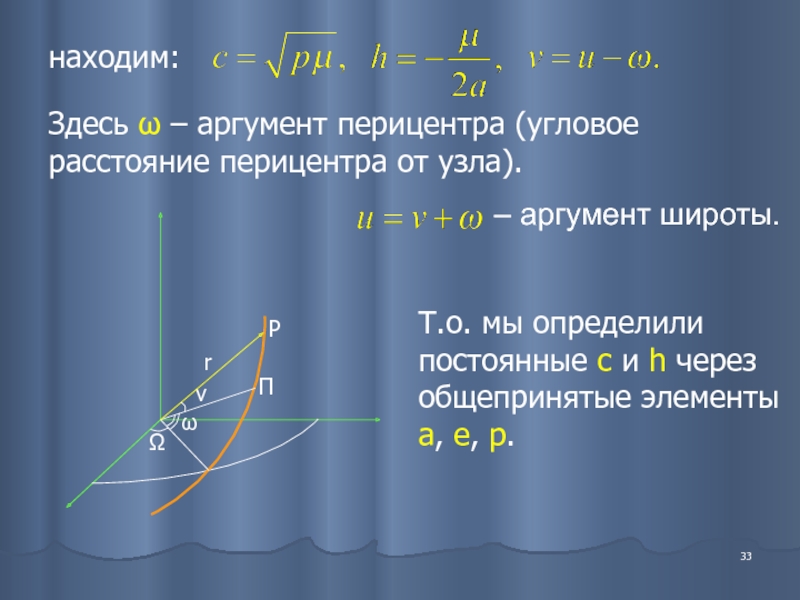
Слайд 33находим:
Здесь ω – аргумент перицентра (угловое расстояние перицентра от узла).
– аргумент
широты.
Т.о. мы определили постоянные c и h через общепринятые элементы a, e, p.
Слайд 34С этими постоянными интеграл энергии
Уравнение траектории
(19)
(20)
(21)
Уравнение интеграла площадей:
Слайд 35Введем для случая эллиптического движения некоторую вспомогательную переменную – эксцентрическую аномалию
E:
Из рис. видно, что
Поэтому:
Т.е.
(22)
Слайд 36Отношение малой и большой полуоси будет:
Здесь
Отсюда имеем:
(23)
Возводя (22) и (23) в
квадрат и складывая, получим:
(24)
(см. след. слайд)
Слайд 38Подставляя (24) в (22) и (23), получим соотношения, связывающие истинную и
эксцентрическую аномалии:
(25)
Можно найти также соотношения, связывающие тангенсы половинных углов v и E:
Слайд 39Делим первое на второе:
Используя тригонометрические соотношения
окончательно находим:
(26)
(25’)
Слайд 40Найдем теперь уравнение, связывающее переменную E со временем. Дифференцируя соотношение (26)
получим:
Отсюда
Слайд 42Используя также выражение для радиус-вектора (24)
Откуда имеем
и второе из соотношений (25’)
находим:
Слайд 43Интегрируя, находим:
(27)
Здесь
– постоянная интегрирования (момент прохождения через перигелий), а само уравнение
– знаменитое уравнение Кеплера.
Чтобы связать движение в плоскости орбиты с движением в пространстве, надо сделать еще один поворот системы координат.
Слайд 45Таким образом, получить выражения для координат x, y, z через элементы
орбиты можно при помощи трех поворотных матриц:
Сокращенно это можно записать так:
где
– матрица, соответствующая повороту
вокруг оси абсцисс на угол
, а
и
матрицы поворота вокруг оси аппликат на угол
и угол
соответственно.
(28)
Слайд 46Так как движение в задаче двух тел происходит в плоскости, то
в прямоугольной орбитальной системе координат {ξ, η, ζ} координата ζ=0, а координаты ξ и η, как это следует из рисунка на слайде 35 и соотношений (22) и (23)
(29)
Слайд 47Уравнение Кеплера, связывающее эксцентрическую аномалию и время, обычно записывают в виде:
где
Величина
есть
среднее движение
по орбите.
средняя аномалия
Среднюю аномалию обычно представляют в виде
где
