- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Высшая математика. Лекция 2. Обратная матрица презентация
Содержание
- 1. Высшая математика. Лекция 2. Обратная матрица
- 2. Пусть А – невырожденная (det A≠0) квадратная
- 3. Теорема. ( О существовании обратной матрицы).
- 4. Теорема. Всякая невырожденная матрица имеет единственную обратную матрицу: Aij – алгебраическое дополнение элемента aij.
- 5. Δ≠0. Обратная матрица: n =2.
- 6. Обратная матрица: n = 3.
- 8. Пример Найти обратную матрицу к матрице Решение
- 9. Пример Найти обратную матрицу к матрице Решение
- 10. Пример Найти обратную матрицу к матрице Решение
- 11. Пример Найти обратную матрицу к матрице Решение
- 12. Пример Найти обратную матрицу к матрице Решение
- 13. Пример Найти обратную матрицу к матрице Решение
- 14. Пример Найти обратную матрицу к матрице Решение
- 15. Пример Найти обратную матрицу к матрице Решение
- 16. Пример Найти обратную матрицу к матрице Решение
- 17. Пример Найти обратную матрицу к матрице Решение
- 18. 4. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
- 19. К решению систем линейных алгебраических уравнений
- 20. Системой линейных алгебраических уравнений, содержащей т уравнений
- 21. Решением системы (2.1) будем называть упорядоченный набор
- 22. (2.3)
- 23. Решить систему — значит найти все ее решения или доказать, что решений нет.
- 24. несовместная определенная неопределенная ∃ более
- 25. В случае неопределенной СЛАУ каждое ее
- 26. Система, у которой все свободные члены
- 27. Если число уравнений системы совпадает с числом
- 28. 4.1. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ РЕШЕНИЯ СЛАУ
- 29. Применение обратной матрицы для решения
- 30. Пример. Решить матричным способом систему уравнений Решение.
- 31. 4.2. Метод Крамера
- 32. Габриэль Крамер швейцарский математик, один из создателей линейной алгебры (1704 -1752)
- 34. Введем в рассмотрение следующие три определителя
- 35. : Cогласно (2.9),
- 37. Рассмотрим систему трех линейных уравнений с
- 38. Теорема (правило Крамера).
- 39. Окончание лекции
Пусть А – невырожденная (det A≠0)
квадратная матрица (1.2) порядка n. Е – единичная матрица того же порядка. Матрица А–1 называется обратной
к матрице А, если выполняются равенства 3. Обратная
Слайд 2Пусть А – невырожденная (det A≠0)
квадратная матрица (1.2) порядка n.
Е –
единичная матрица того же порядка.
Матрица А–1 называется обратной
к матрице А, если выполняются равенства
3. Обратная матрица
Слайд 3Теорема.
( О существовании обратной матрицы).
Матрица А имеет обратную тогда и
только тогда,
когда ее определитель отличен от нуля (det A≠0,
т.е. когда матрица является невырожденной).
когда ее определитель отличен от нуля (det A≠0,
т.е. когда матрица является невырожденной).
Слайд 4Теорема.
Всякая невырожденная матрица
имеет единственную обратную матрицу:
Aij – алгебраическое дополнение элемента aij.
Слайд 19
К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи (по
некоторым оценкам более 75% всех задач).
Слайд 20Системой линейных алгебраических уравнений, содержащей т уравнений и n неизвестных, называется
система вида
(2.1)
где x1, x2, …, xn – неизвестные,
aij– числа (i = 1, …, m; j =1, …, n), называемые коэффициентами системы,
b1, b2, …, bm – числа, называемые свободными членами.
(2.1)
где x1, x2, …, xn – неизвестные,
aij– числа (i = 1, …, m; j =1, …, n), называемые коэффициентами системы,
b1, b2, …, bm – числа, называемые свободными членами.
Слайд 21Решением системы (2.1) будем называть упорядоченный набор чисел x1, x2, …, xn , обращающий
каждое ее уравнение в верное равенство.
Такую систему удобно записывать в компактной матричной форме: А⋅ Х=В. (2.2)
Такую систему удобно записывать в компактной матричной форме: А⋅ Х=В. (2.2)
– матрица коэффициентов системы.
— вектор-столбец из неизвестных xj .
— (столбец правых частей)
вектор-столбец из
свободных членов bi.
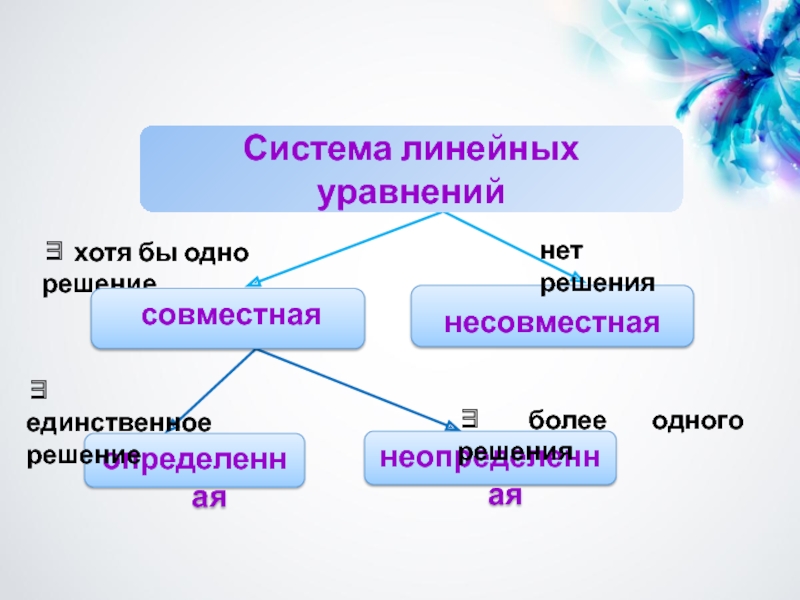
Слайд 24
несовместная
определенная
неопределенная
∃ более одного решения
∃ единственное решение
нет решения
∃ хотя бы одно
решение
Система линейных уравнений
совместная
Слайд 25
В случае неопределенной СЛАУ каждое ее решение называется частным решением.
Совокупность
всех частных решений называется общим решением.
Слайд 26
Система, у которой все свободные члены равны нулю
(b1 = b2
=…= bn = 0), называется однородной.
Однородная система всегда совместна, так как набор из n нулей (тривиальное решение) удовлетворяет любому уравнению из (2.4).
Однородная система всегда совместна, так как набор из n нулей (тривиальное решение) удовлетворяет любому уравнению из (2.4).
Слайд 27Если число уравнений системы совпадает с числом неизвестных (m=n), то система
называется квадратной.
Если определитель матрицы A квадратной системы Δ =det A≠ 0, то система имеет единственное решение.
Если det A= 0, то система либо имеет бесконечное множество решений, либо несовместна.
Если определитель матрицы A квадратной системы Δ =det A≠ 0, то система имеет единственное решение.
Если det A= 0, то система либо имеет бесконечное множество решений, либо несовместна.
Слайд 29
Применение обратной матрицы
для решения СЛАУ
В матричной форме записи квадратная определенная
система уравнений имеет вид:
АХ=В. (2.2*)
Так как det А=Δ≠0, существует обратная матрица А–1.
Если умножить обе части (2.2*) на А–1 слева, то получим формулу для нахождения столбца неизвестных Х:
АХ=В. (2.2*)
Так как det А=Δ≠0, существует обратная матрица А–1.
Если умножить обе части (2.2*) на А–1 слева, то получим формулу для нахождения столбца неизвестных Х:
⇒
Слайд 33
. (2.7)
Метод Крамера
Пусть квадратная определенная система в матричной форме
имеет вид : АХ=В, det А=Δ≠0. (2.6)
Тогда из (2.5) получим, что решение (2.6) находится по формулам:
Тогда из (2.5) получим, что решение (2.6) находится по формулам:
где ,
⇒
Формулы (2.7) отыскания решения системы (2.6) называются формулами Крамера.
определитель матрицы, полученной из А заменой ее
j-го столбца на столбец правых частей системы, j=1, 2,..n.
Слайд 34
Введем в рассмотрение следующие три определителя для матрицы системы (2.8):
Теорема (правило Крамера).
Если Δ ≠ 0, то система (2.8) имеет единственное решение, которое находится по формулам
(2.9)
Частный случай n=2. (2.8)
Слайд 35:
Cогласно (2.9), получаем
Пример. Решить по правилу Крамера систему уравнений
Решение. Вычислим
определитель системы
Слайд 37
Рассмотрим систему трех линейных уравнений с тремя неизвестными
(2.10)
n=3.
Обозначим
Вспомогательные определители Δ1, Δ2, Δ3 получаются из определителя Δ матрицы системы (2.10) заменой соответствующего столбца столбцом свободных членов.
Слайд 38
Теорема (правило Крамера). Если Δ ≠ 0, то система (2.10)
имеет единственное решение, которое находится по формулам Крамера
(2.11)
(2.11)
n = 3.
