- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение поверхностей, метод вспомогательных концентрических сфер презентация
Содержание
- 1. Пересечение поверхностей, метод вспомогательных концентрических сфер
- 2. Для применения метода концентрических сфер необходимо выполнение
- 3. Алгоритм решения 2 ГПЗ. Находим центр
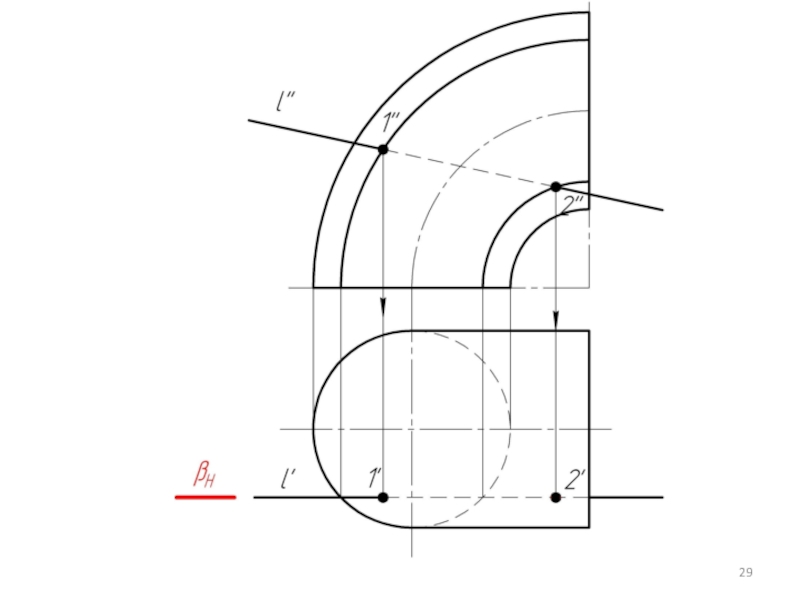
- 20. Лекция 15 «Пересечение прямой с поверхностью (1 ГПЗ)»
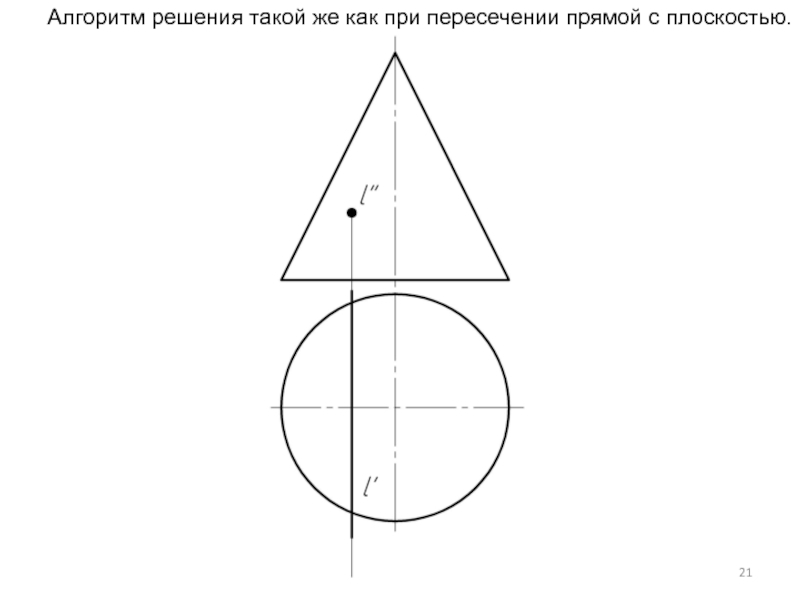
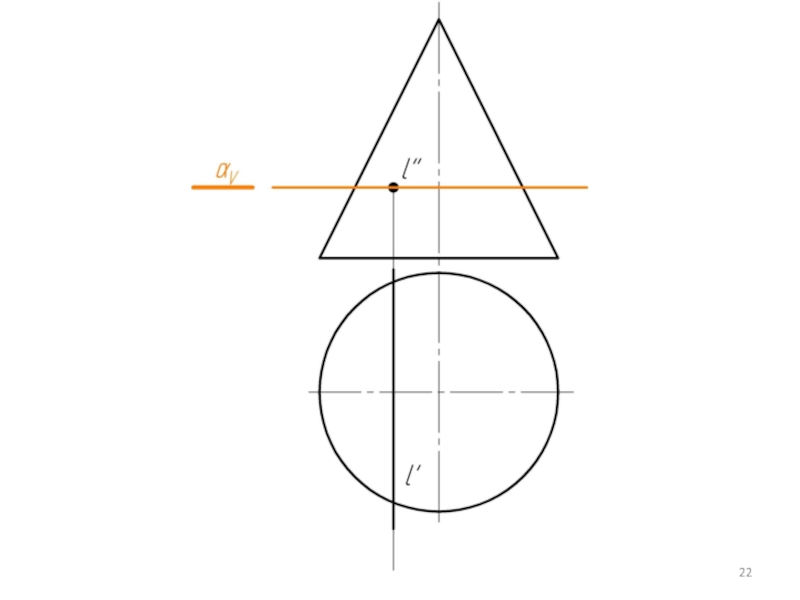
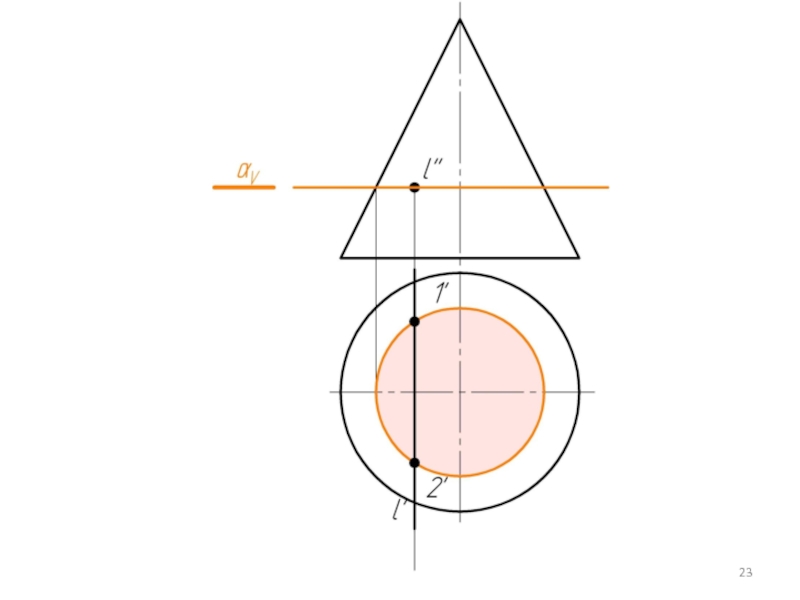
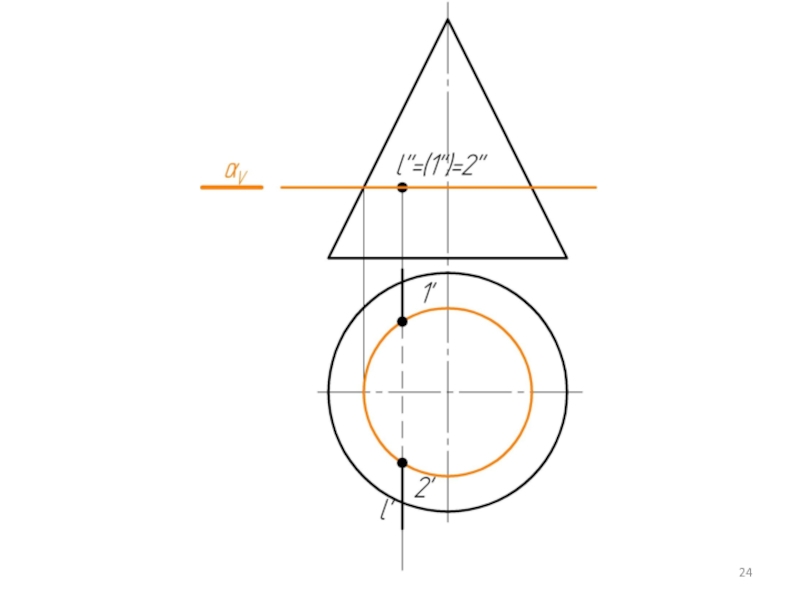
- 21. Алгоритм решения такой же как при пересечении прямой с плоскостью.
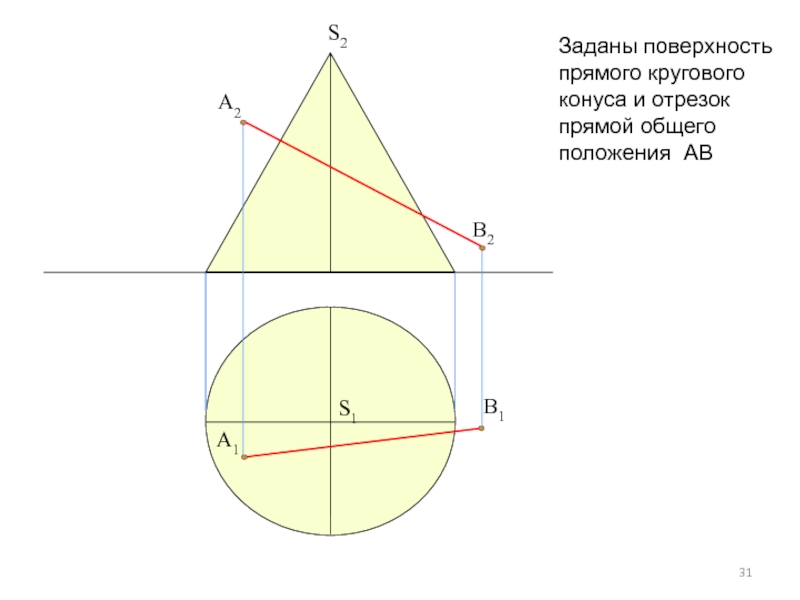
- 30. Условие задачи: Определить точки пересечения
- 31. Заданы
- 32. Для
- 33. Однако,
- 34. α1
- 35. Если
- 36. S A B
- 37. S A B
- 38. S A B
- 39. S A B
- 40. S A B
- 41. S A B
- 42. S A B
- 43. S A B
- 44. S A B
- 45. S A B C D
- 46. S A B C D
Для применения метода концентрических сфер необходимо выполнение трех условий: 1) Обе пересекающиеся поверхности должны быть поверхностями вращения; 2) Оси поверхностей должны пересекаться; 3) Поверхности должны иметь общую плоскость симметрии, т.е.оси поверхностей
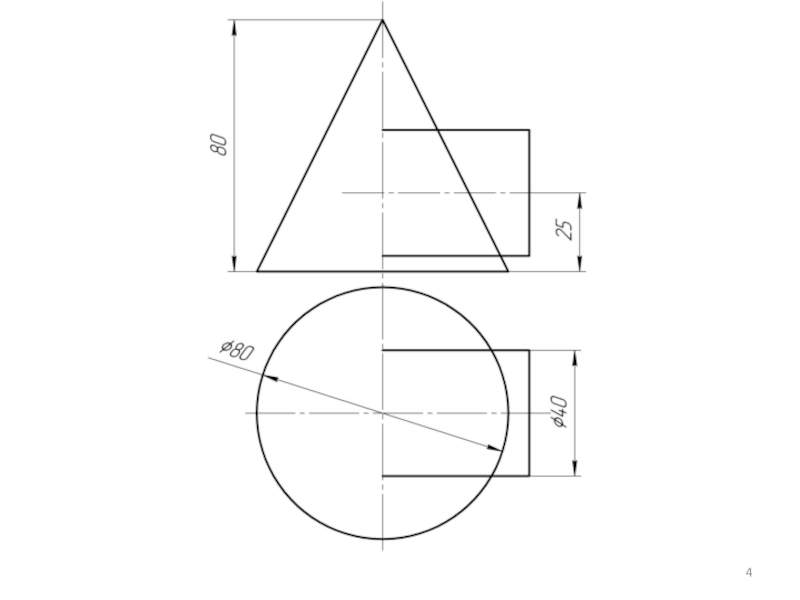
Слайд 2 Для применения метода концентрических сфер необходимо выполнение трех условий:
1) Обе пересекающиеся
поверхности должны быть поверхностями вращения;
2) Оси поверхностей должны пересекаться;
3) Поверхности должны иметь общую плоскость симметрии, т.е.оси поверхностей должны лежать в одной плоскости.
2) Оси поверхностей должны пересекаться;
3) Поверхности должны иметь общую плоскость симметрии, т.е.оси поверхностей должны лежать в одной плоскости.
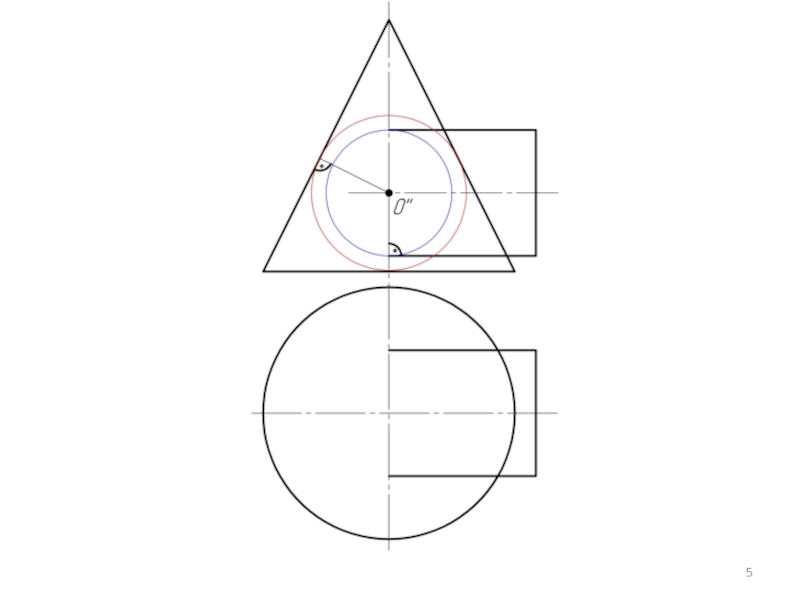
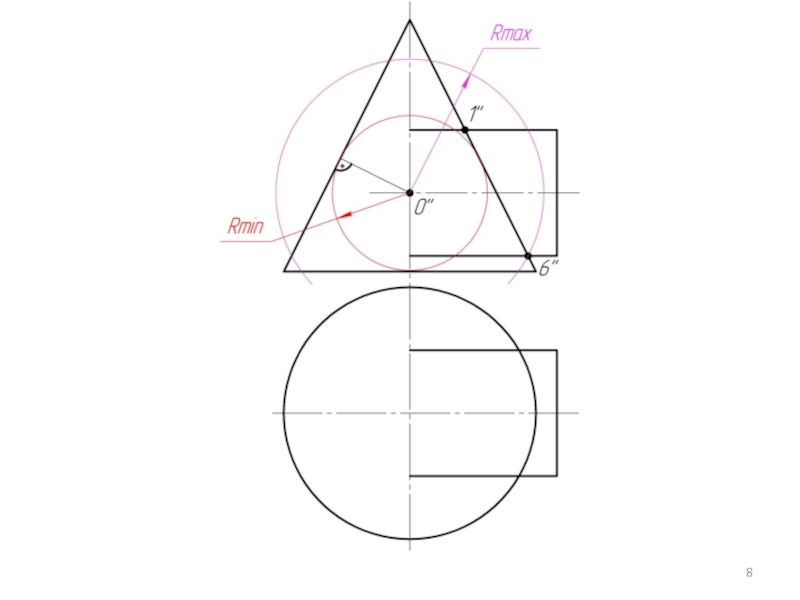
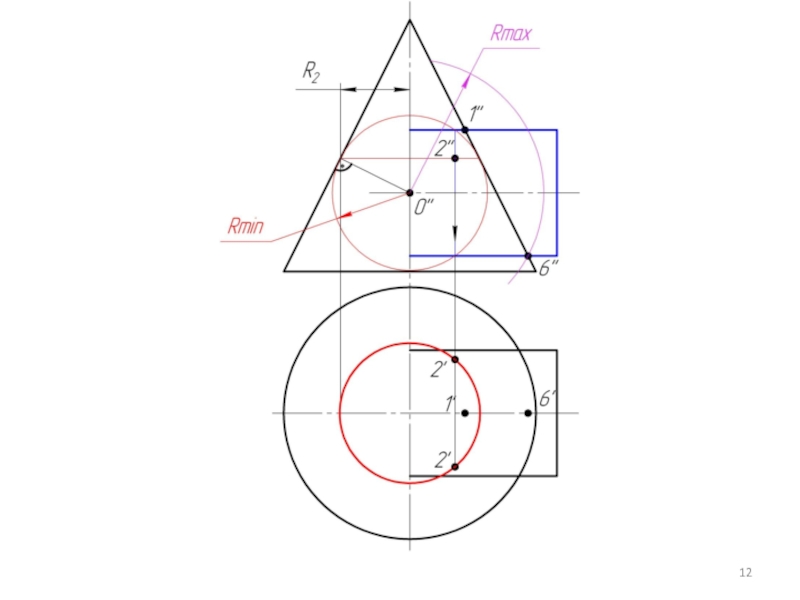
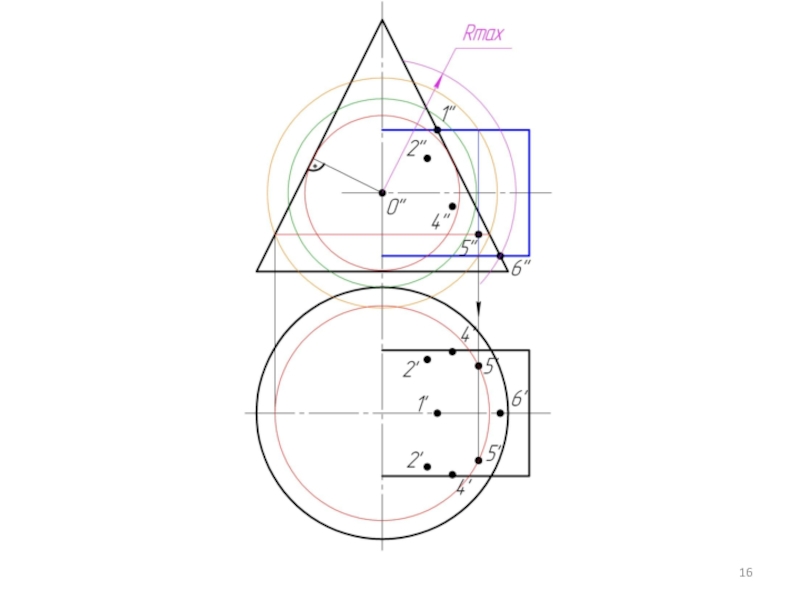
Слайд 3 Алгоритм решения 2 ГПЗ.
Находим центр секущих сфер – точку пересечения осей
вращения заданных поверхностей.
Находим минимальный радиус сферы (Rmin). Сфера минимального радиуса должна одну поверхность пресекать, а другой касаться, т.е. быть вписанной.
Находим радиус максимальной секущей сферы, она должна проходить через самую дальнюю точку пересечения очерков поверхностей.
Строим линии пересечения сферы Rmin с заданными поверхностями.
Определяем точки пресечения построенных линий.
Произвольно выбираем последовательно ряд промежуточных секущих сфер и повторяем построения по пунктам 4 и 5.
Соединяем точки плавной кривой линией с учетом видимости.
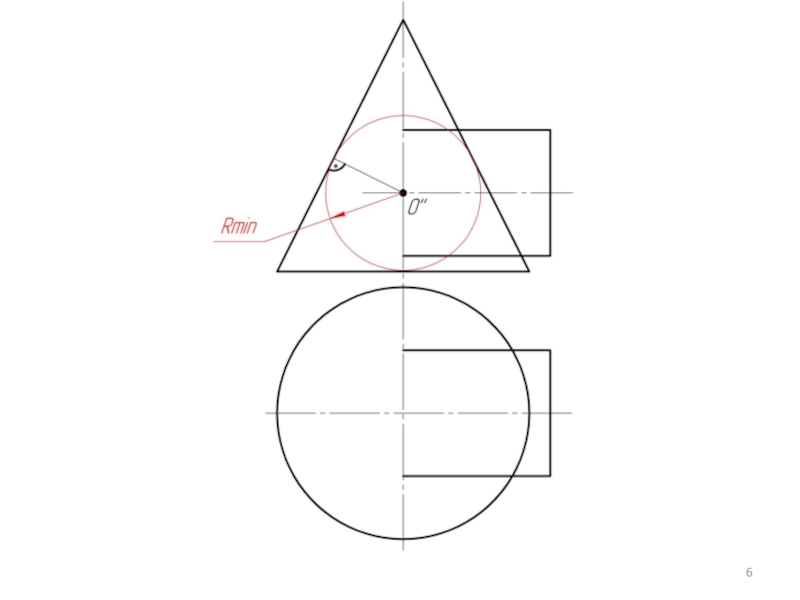
Находим минимальный радиус сферы (Rmin). Сфера минимального радиуса должна одну поверхность пресекать, а другой касаться, т.е. быть вписанной.
Находим радиус максимальной секущей сферы, она должна проходить через самую дальнюю точку пересечения очерков поверхностей.
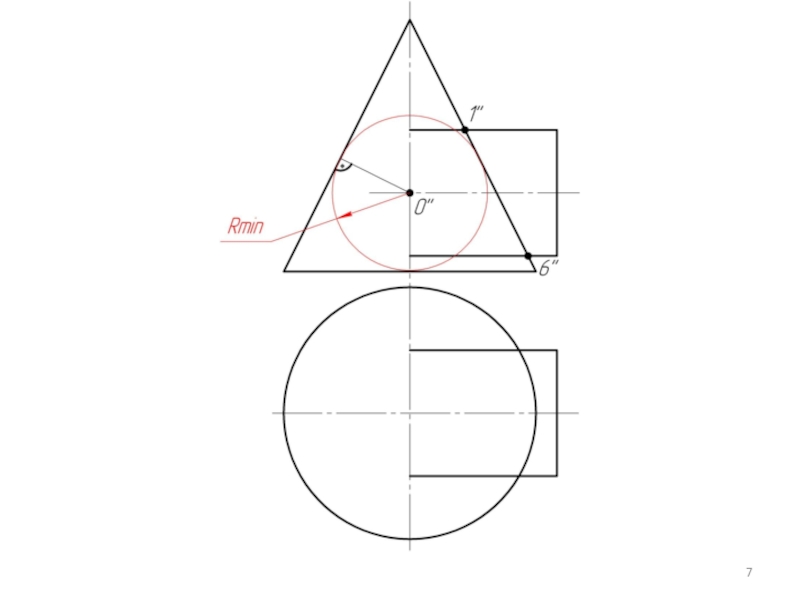
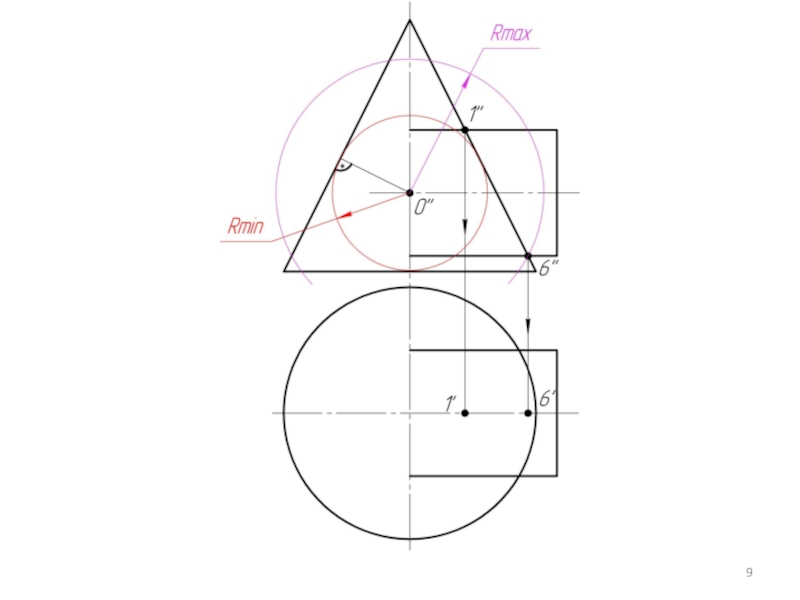
Строим линии пересечения сферы Rmin с заданными поверхностями.
Определяем точки пресечения построенных линий.
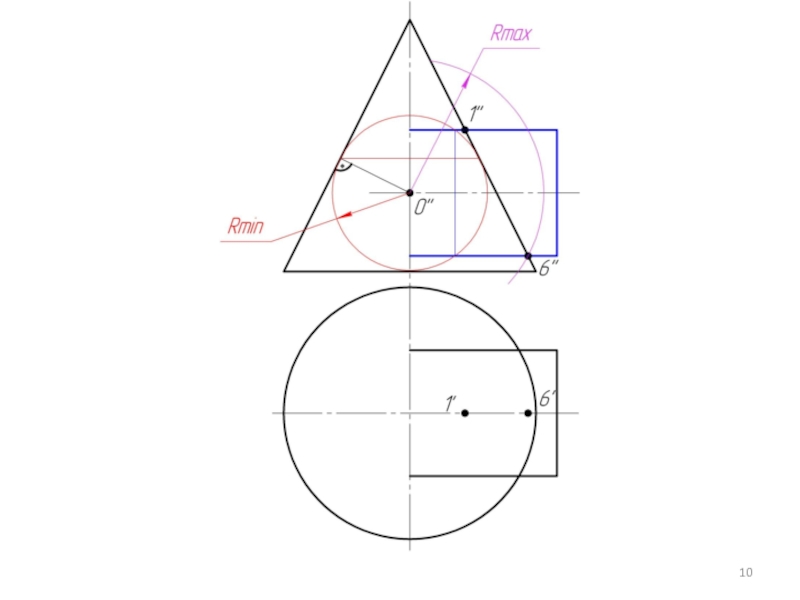
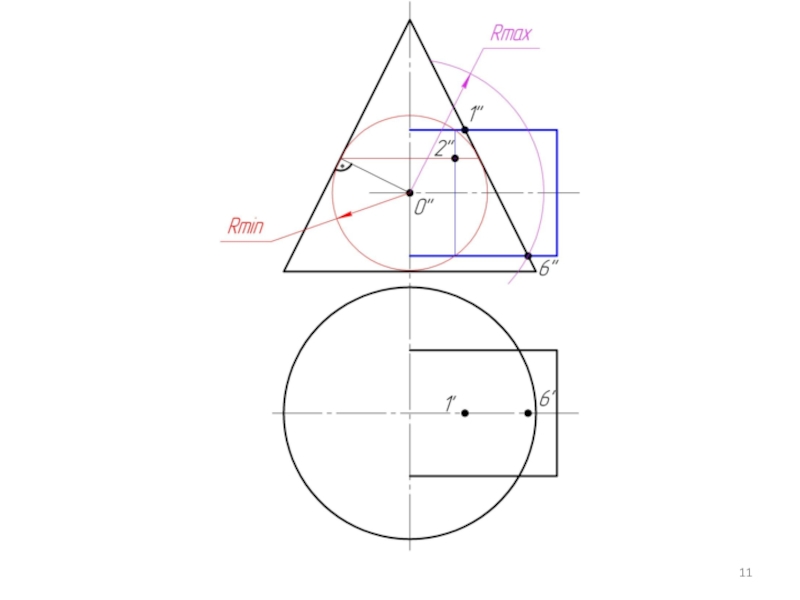
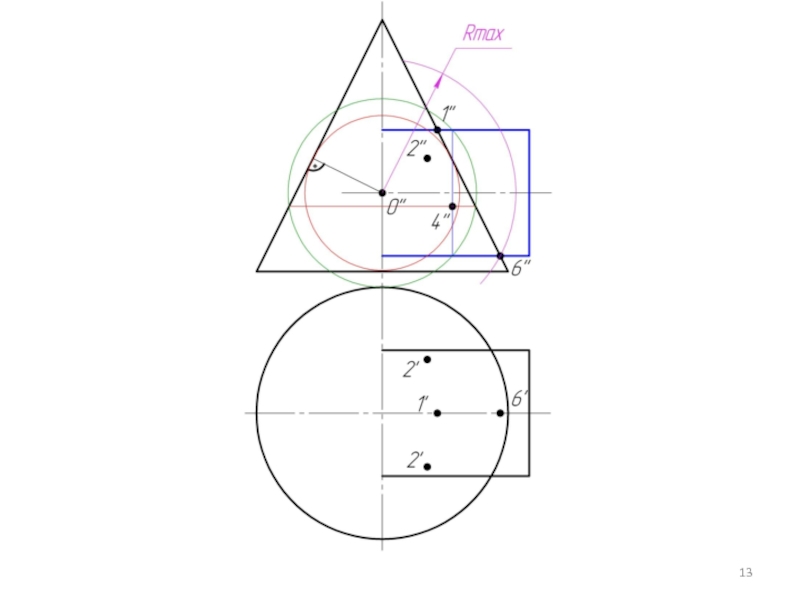
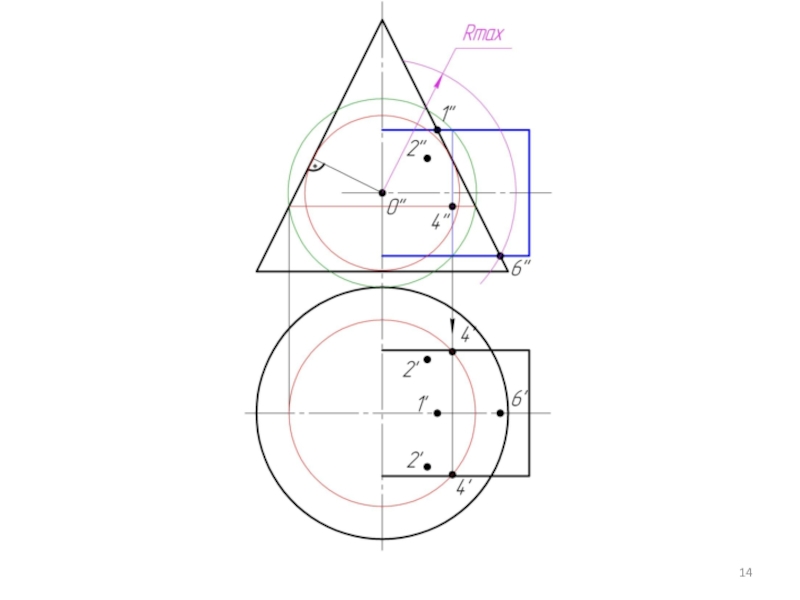
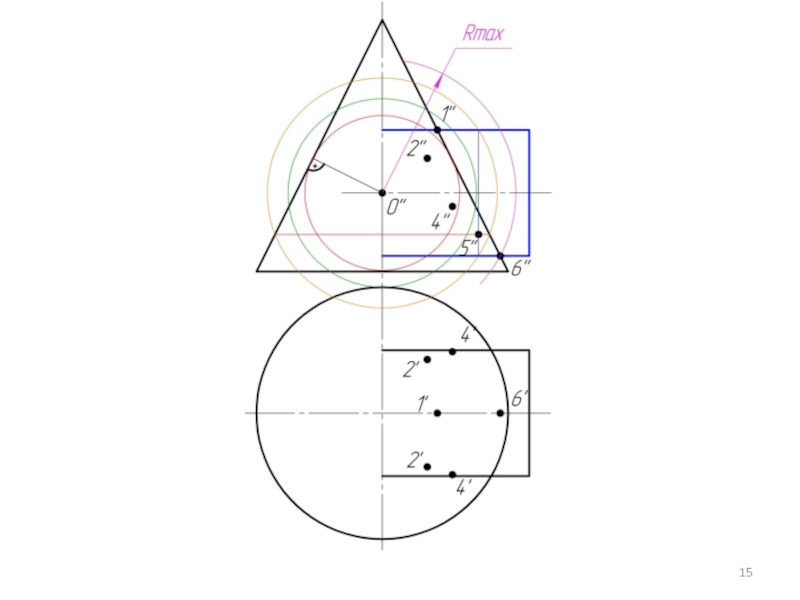
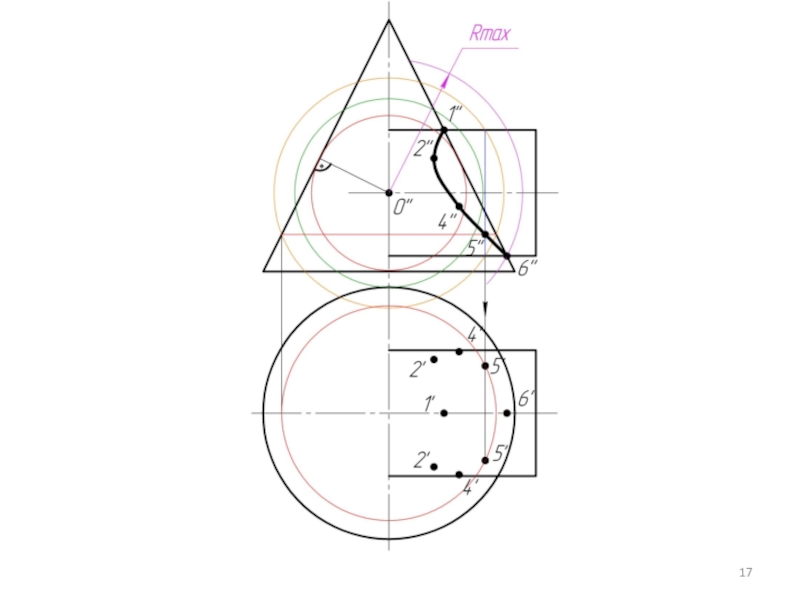
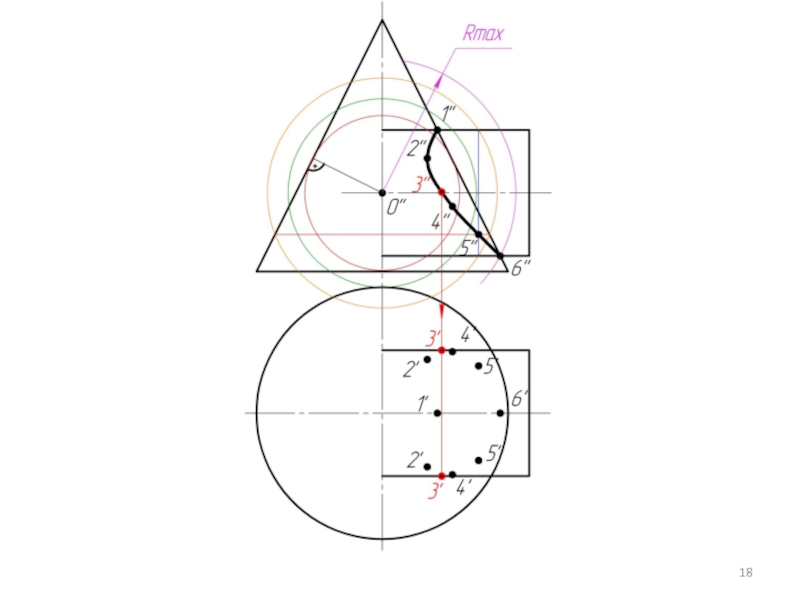
Произвольно выбираем последовательно ряд промежуточных секущих сфер и повторяем построения по пунктам 4 и 5.
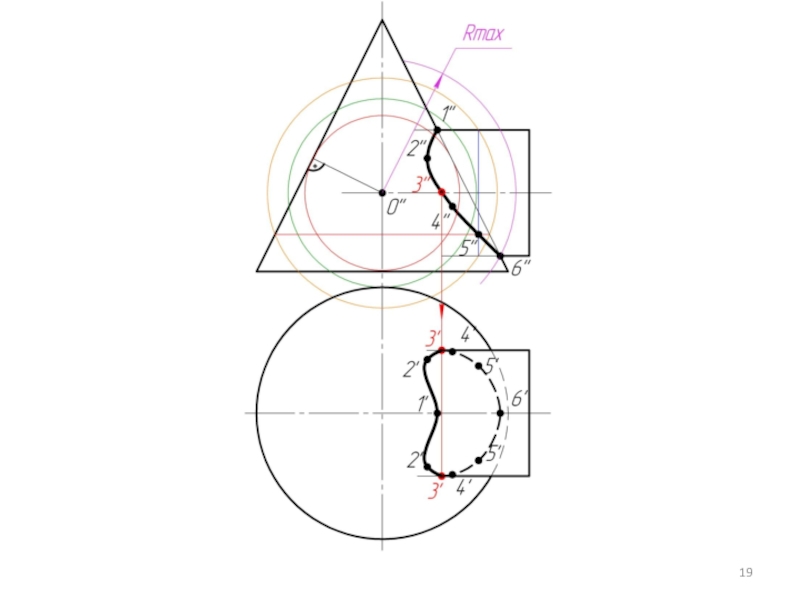
Соединяем точки плавной кривой линией с учетом видимости.
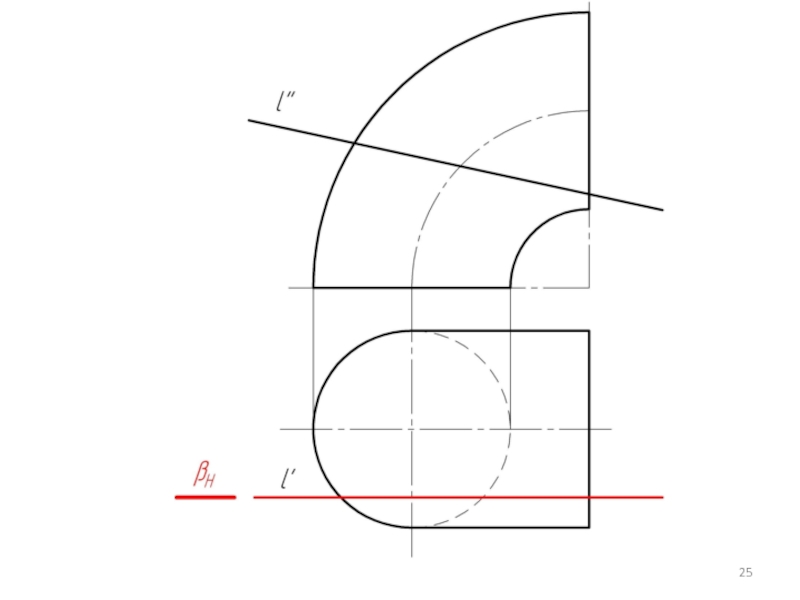
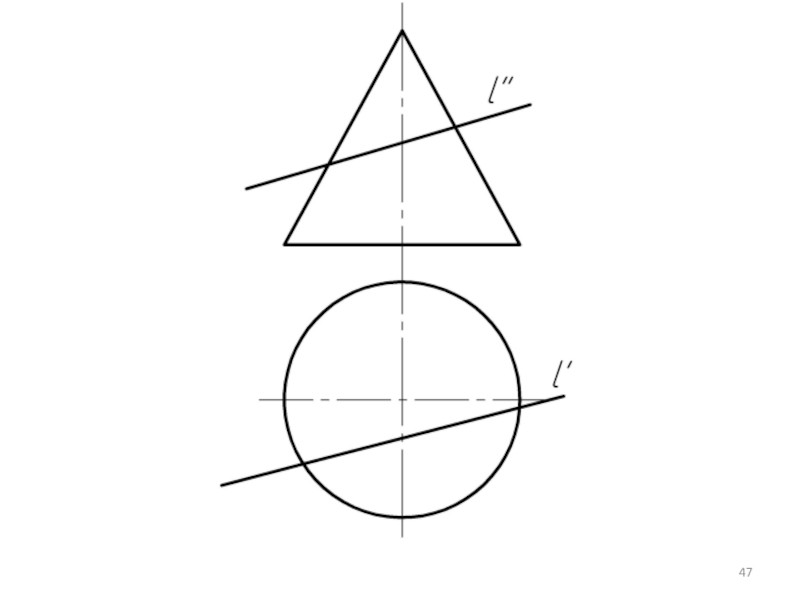
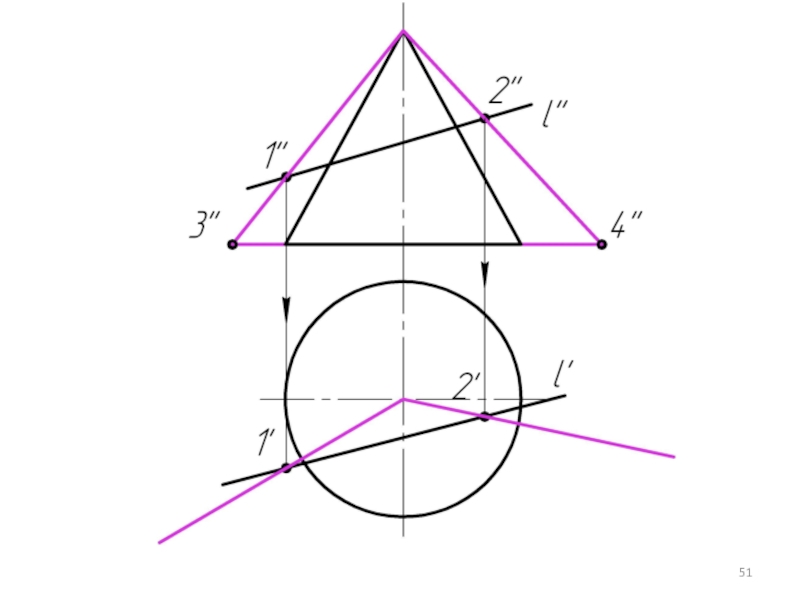
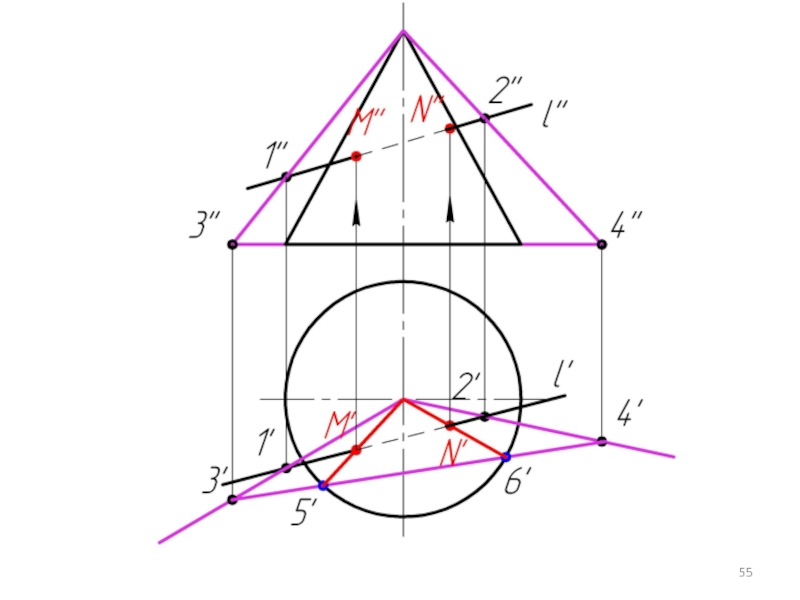
Слайд 30
Условие задачи: Определить точки пересечения прямой, заданной отрезком АВ, с поверхностью.
Решить вопрос видимости прямой.
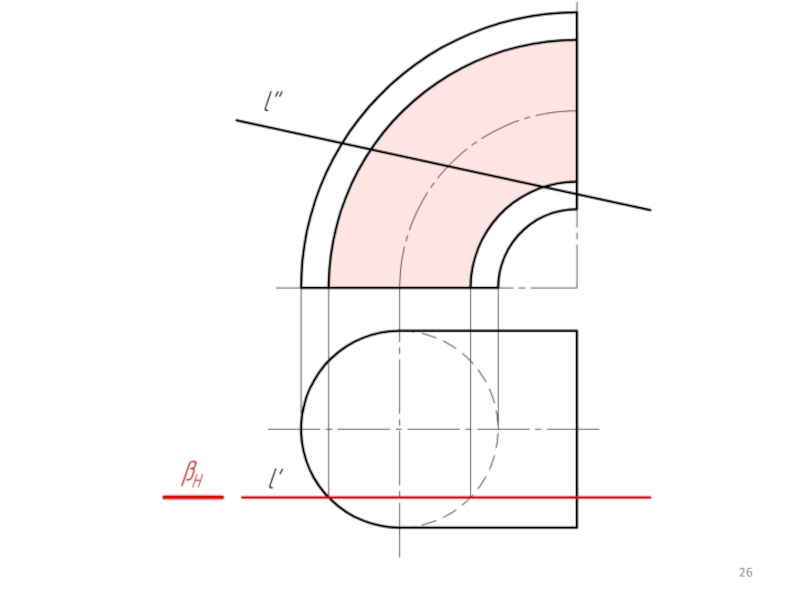
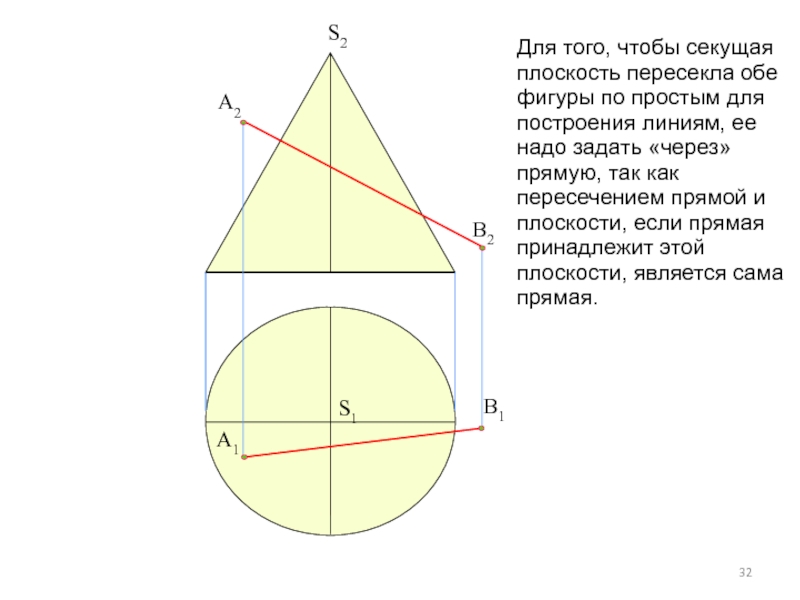
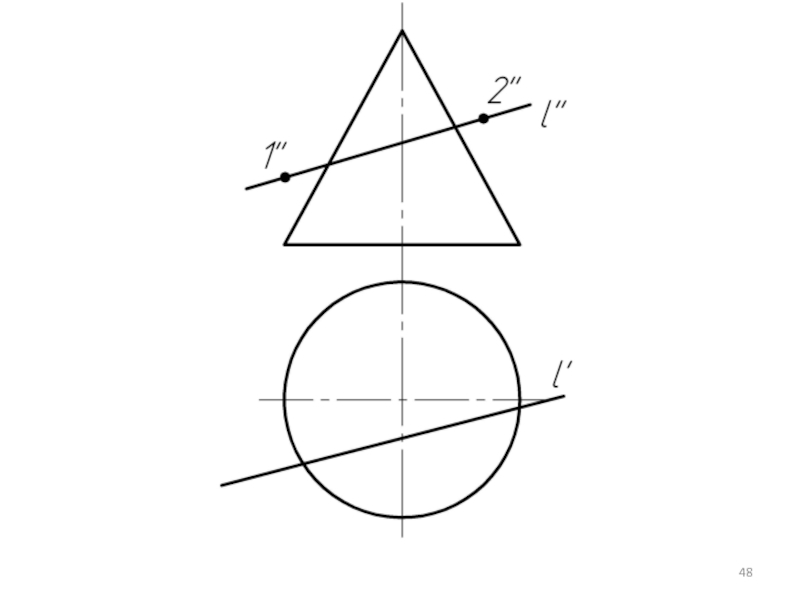
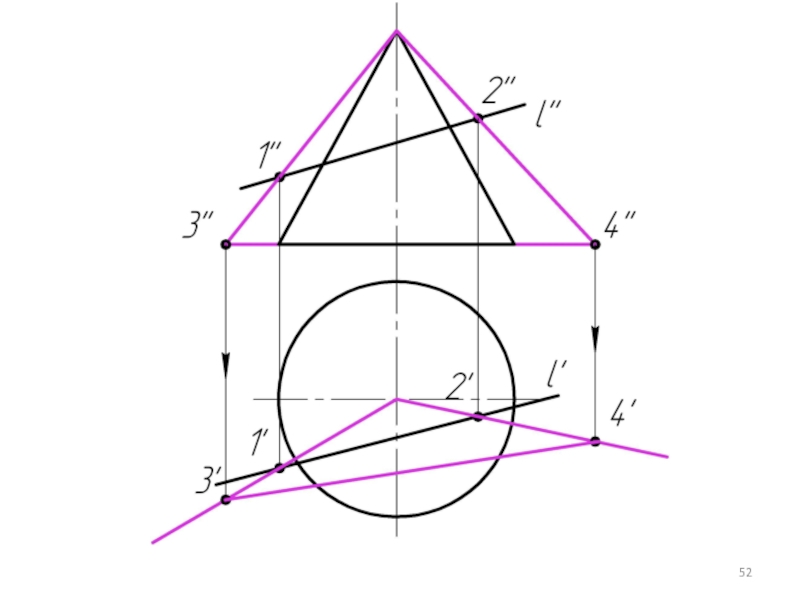
Слайд 32
Для того, чтобы секущая плоскость пересекла обе фигуры по простым для
построения линиям, ее надо задать «через» прямую, так как пересечением прямой и плоскости, если прямая принадлежит этой плоскости, является сама прямая.
S2
S1
A2
A1
B2
B1
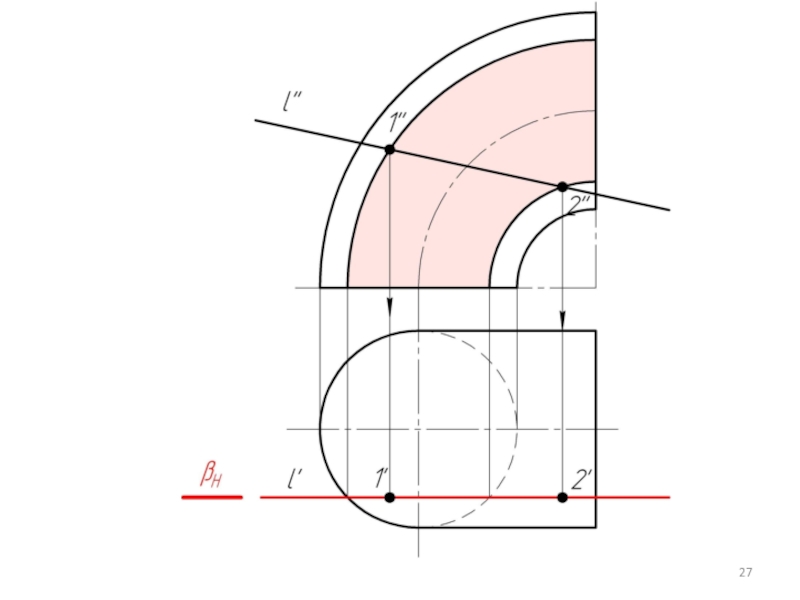
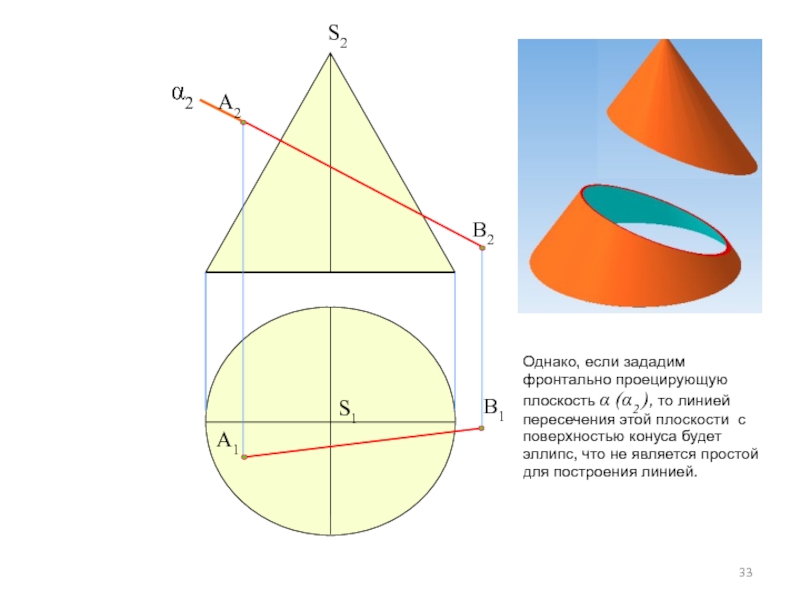
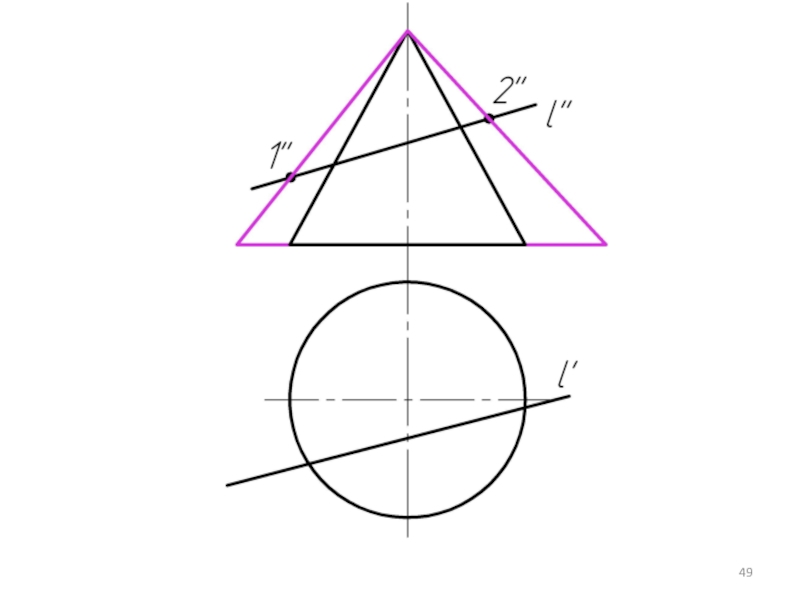
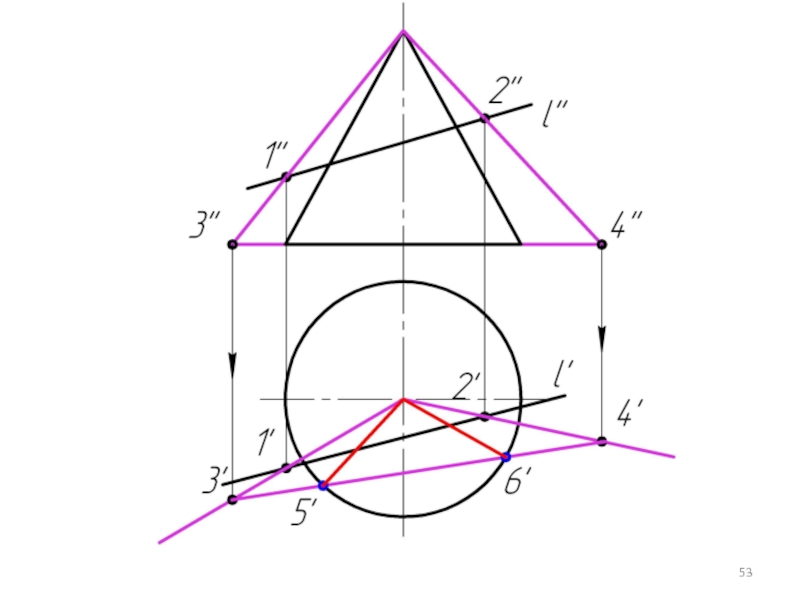
Слайд 33
Однако, если зададим фронтально проецирующую плоскость α (α2 ), то линией
пересечения этой плоскости с поверхностью конуса будет эллипс, что не является простой для построения линией.
α2
S2
S1
A2
A1
B2
B1
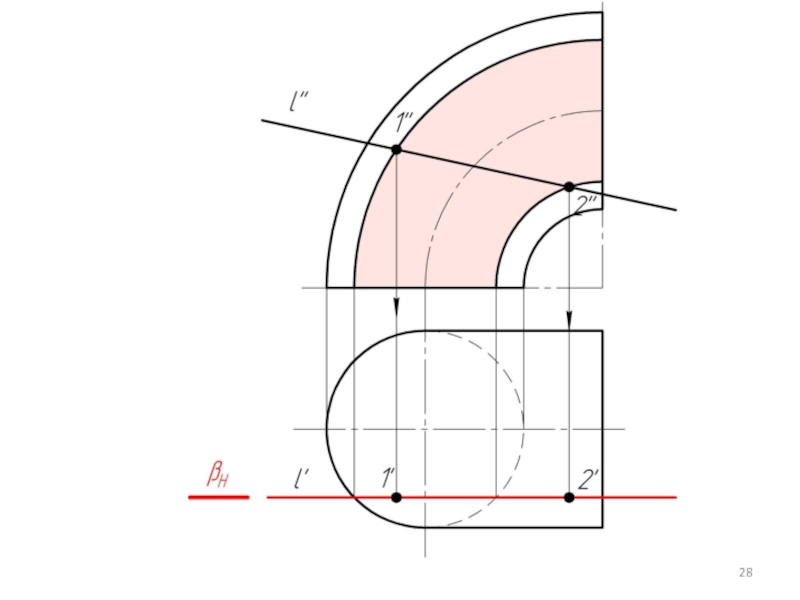
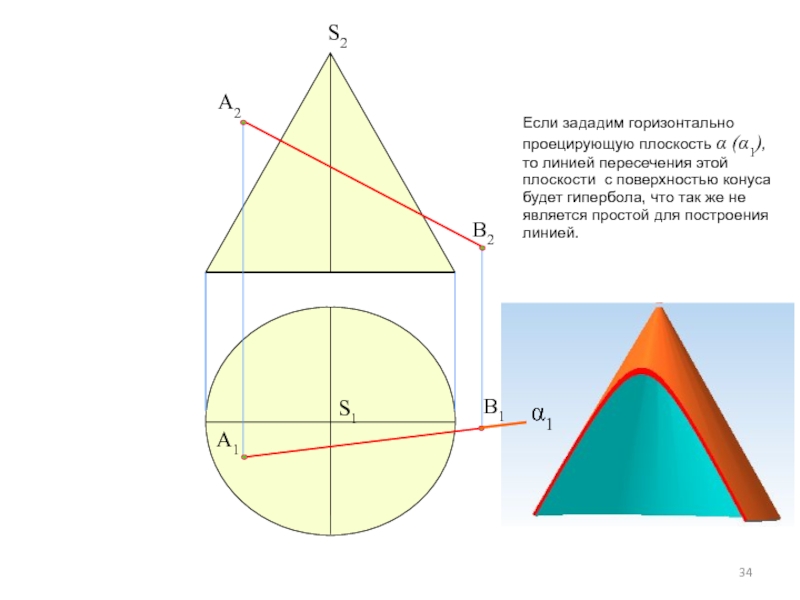
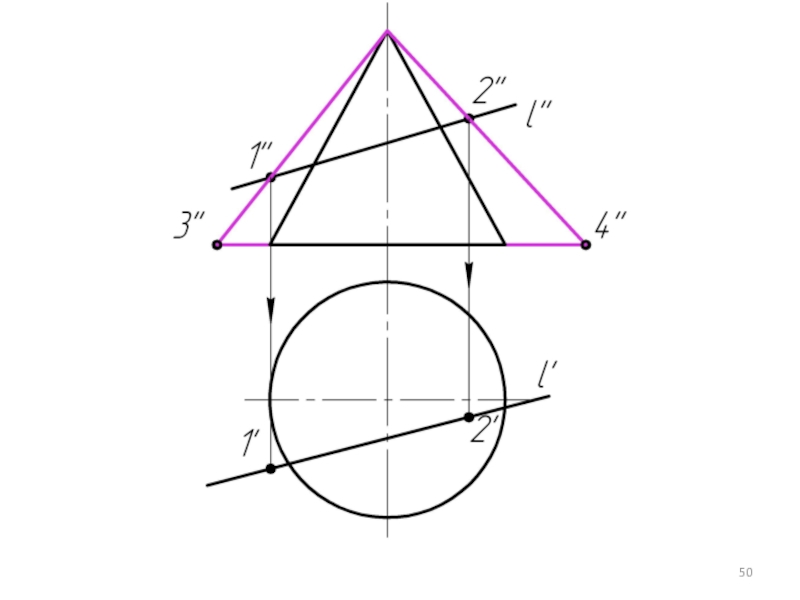
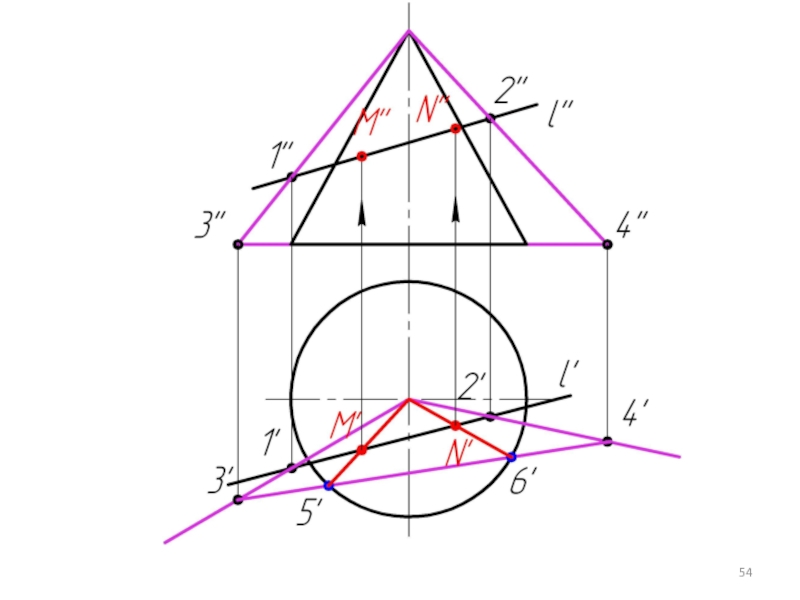
Слайд 34
α1
Если зададим горизонтально проецирующую плоскость α (α1), то линией пересечения этой
плоскости с поверхностью конуса будет гипербола, что так же не является простой для построения линией.
S2
S1
A2
A1
B2
B1
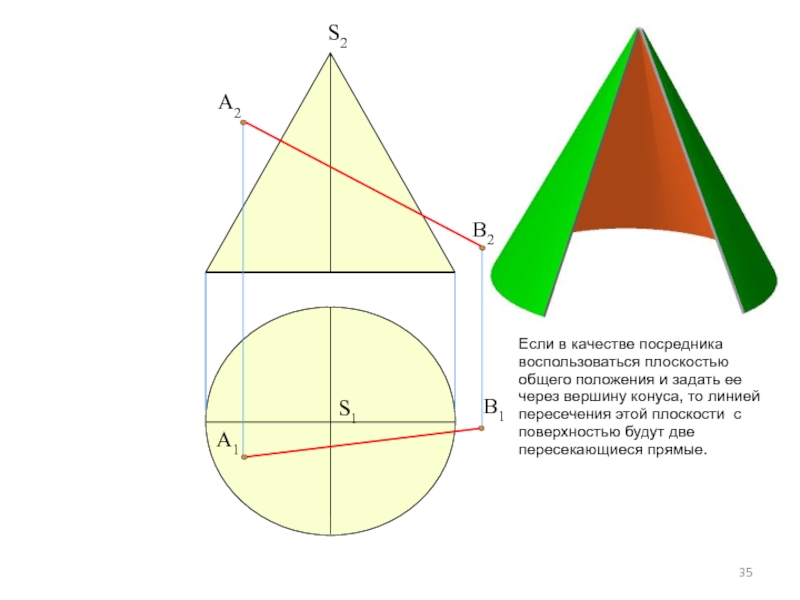
Слайд 35
Если в качестве посредника воспользоваться плоскостью общего положения и задать ее
через вершину конуса, то линией пересечения этой плоскости с поверхностью будут две пересекающиеся прямые.
S2
S1
A2
A1
B2
B1
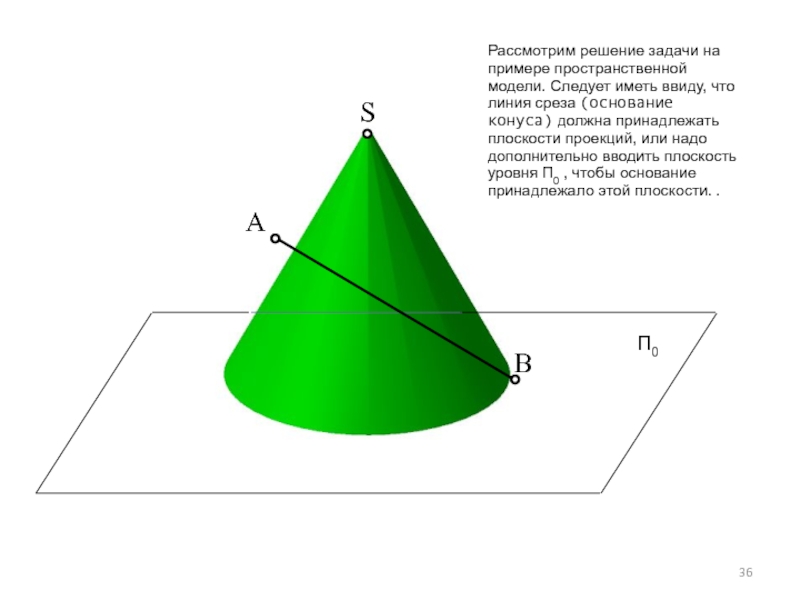
Слайд 36S
A
B
Рассмотрим решение задачи на примере пространственной модели. Следует иметь ввиду, что
линия среза (основание конуса) должна принадлежать плоскости проекций, или надо дополнительно вводить плоскость уровня П0 , чтобы основание принадлежало этой плоскости. .
П0
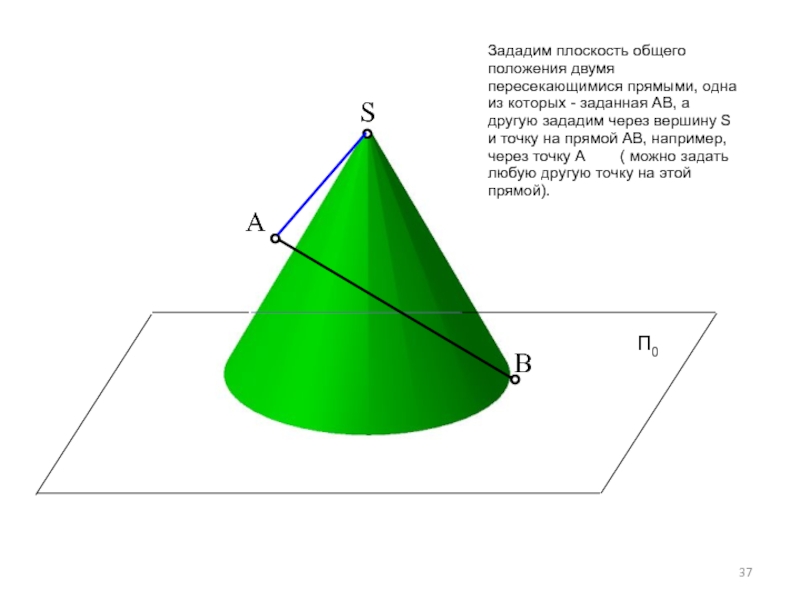
Слайд 37S
A
B
Зададим плоскость общего положения двумя пересекающимися прямыми, одна из которых -
заданная АВ, а другую зададим через вершину S и точку на прямой АВ, например, через точку А ( можно задать любую другую точку на этой прямой).
П0
Слайд 38S
A
B
M
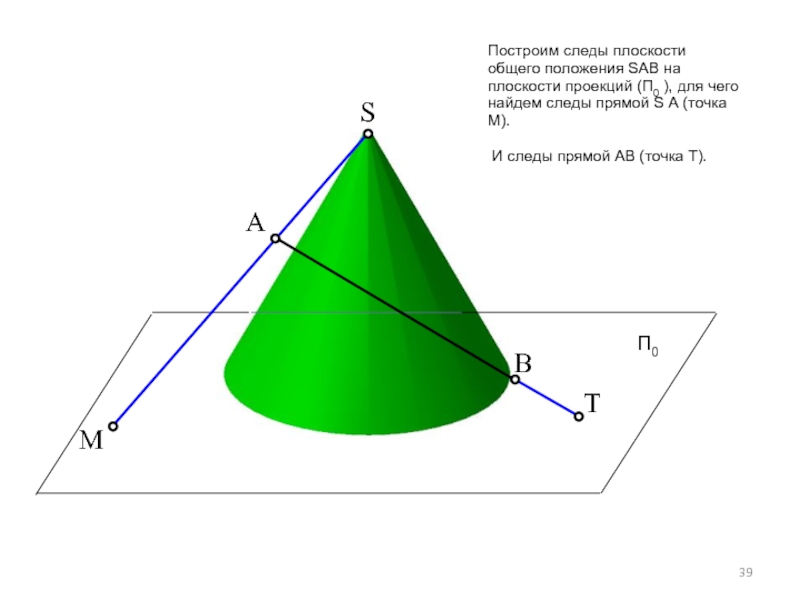
Построим следы плоскости общего положения SАВ на плоскости проекций (П0 ),
для чего найдем следы прямой S А (точка М).
П0
Слайд 39S
A
B
Т
M
Построим следы плоскости общего положения SАВ на плоскости проекций (П0 ),
для чего найдем следы прямой S А (точка М).
И следы прямой АВ (точка Т).
И следы прямой АВ (точка Т).
П0
Слайд 40S
A
B
Т
M
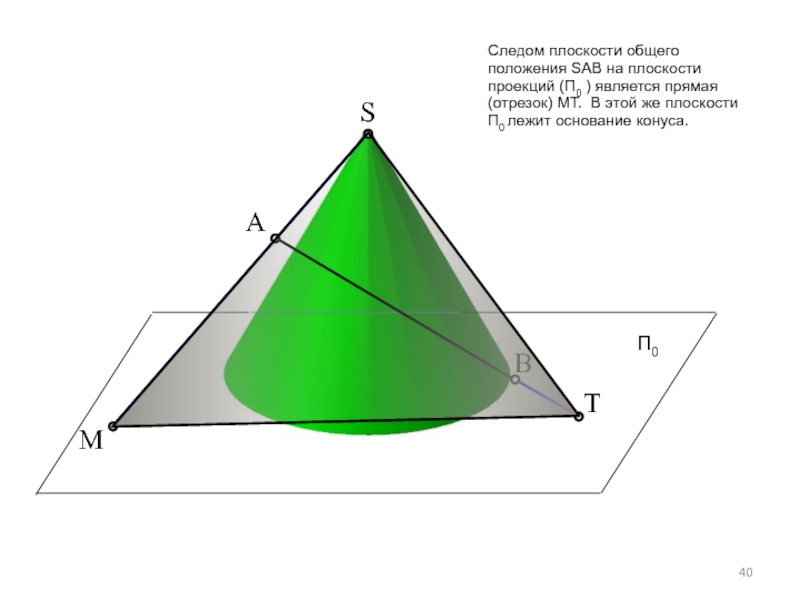
Следом плоскости общего положения SАВ на плоскости проекций (П0 ) является
прямая (отрезок) МТ. В этой же плоскости П0 лежит основание конуса.
П0
Слайд 41S
A
B
Т
M
П0
1
2
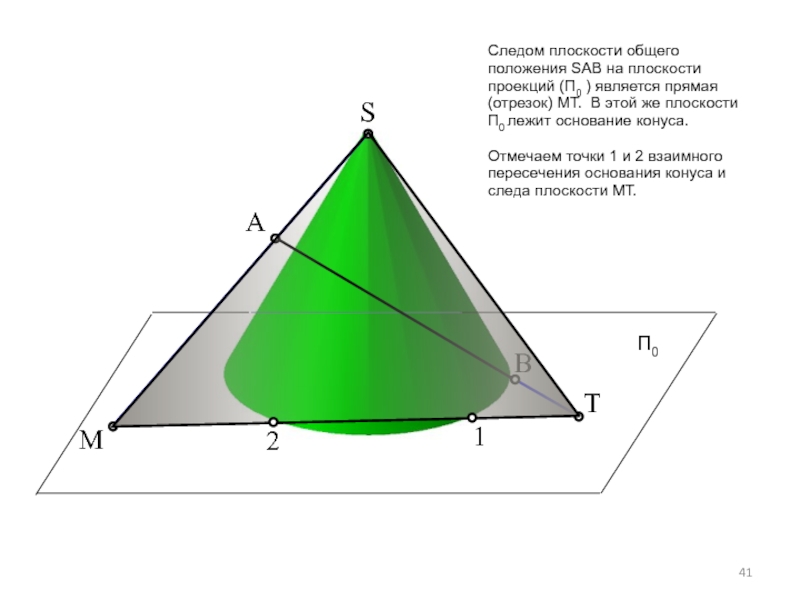
Следом плоскости общего положения SАВ на плоскости проекций (П0 ) является
прямая (отрезок) МТ. В этой же плоскости П0 лежит основание конуса.
Отмечаем точки 1 и 2 взаимного пересечения основания конуса и следа плоскости МТ.
Отмечаем точки 1 и 2 взаимного пересечения основания конуса и следа плоскости МТ.
Слайд 42S
A
B
Т
M
П0
1
2
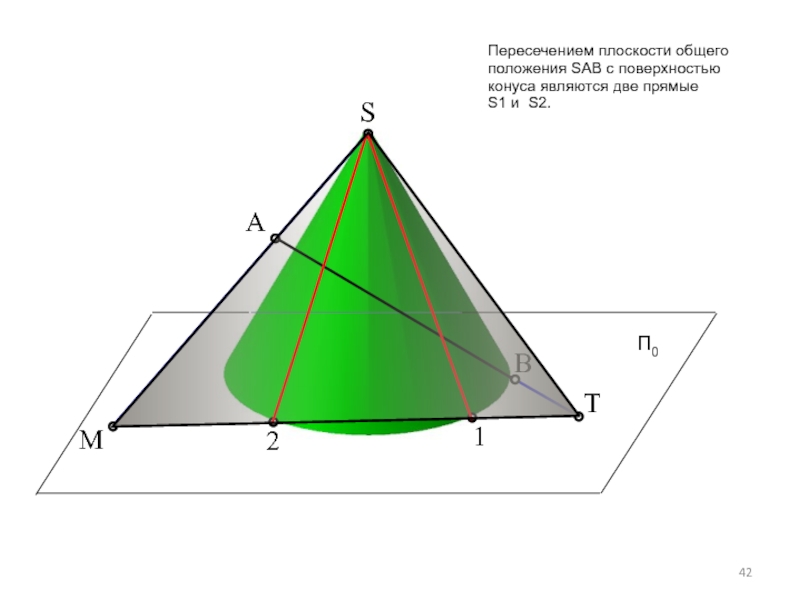
Пересечением плоскости общего положения SАВ с поверхностью конуса являются две прямые
S1 и S2.
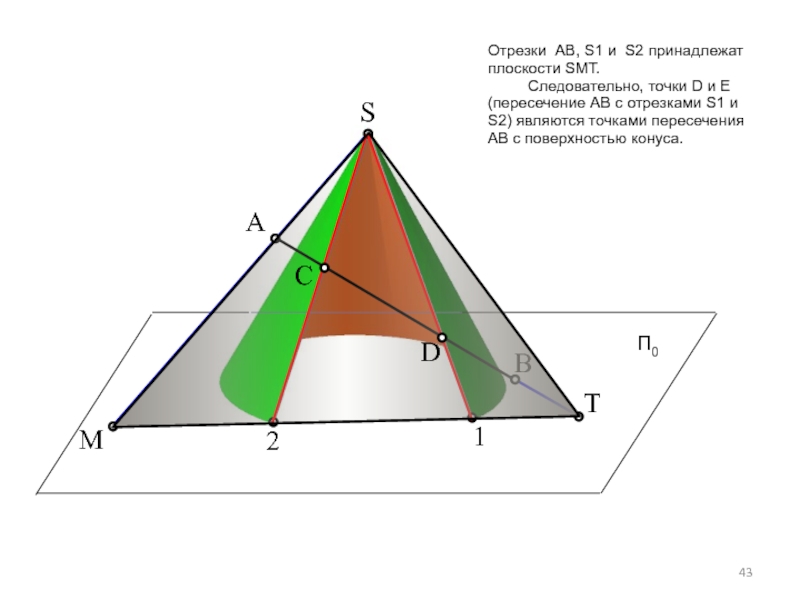
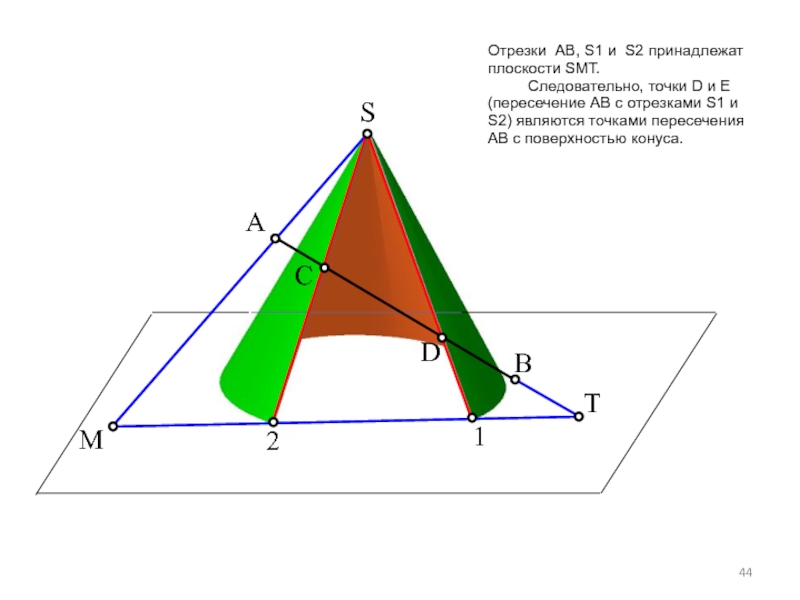
Слайд 43S
A
B
Т
M
П0
1
2
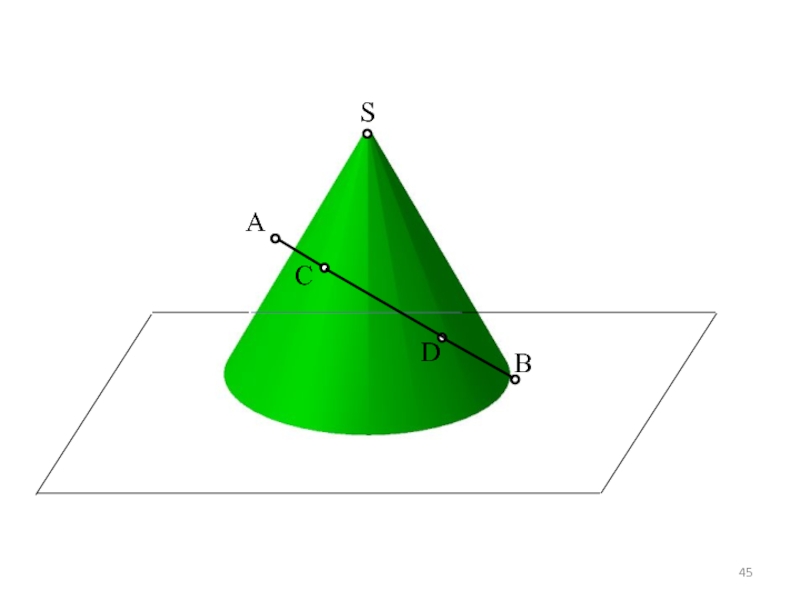
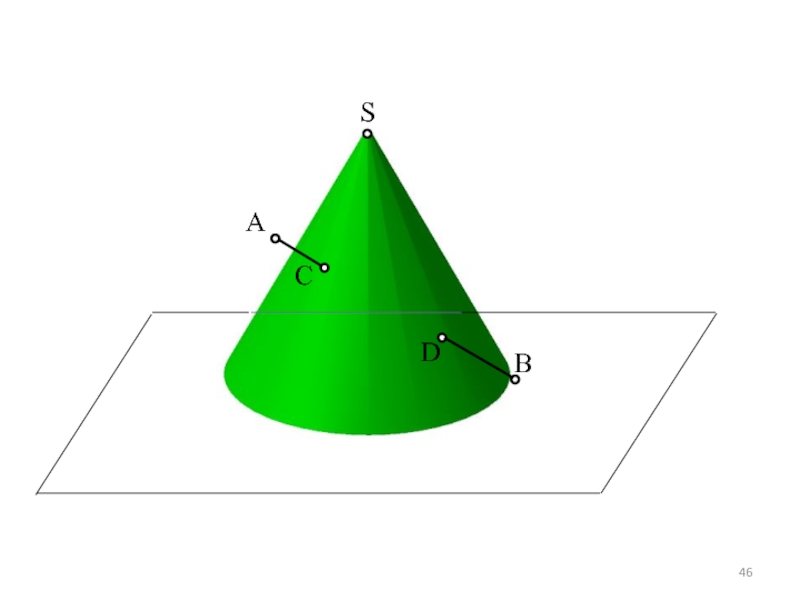
Отрезки АВ, S1 и S2 принадлежат
плоскости SМТ.
Следовательно, точки D и
Е (пересечение АВ с отрезками S1 и S2) являются точками пересечения АВ с поверхностью конуса.
C
D
Слайд 44S
A
B
Т
M
1
2
C
D
Отрезки АВ, S1 и S2 принадлежат
плоскости SМТ.
Следовательно, точки D и
Е (пересечение АВ с отрезками S1 и S2) являются точками пересечения АВ с поверхностью конуса.
