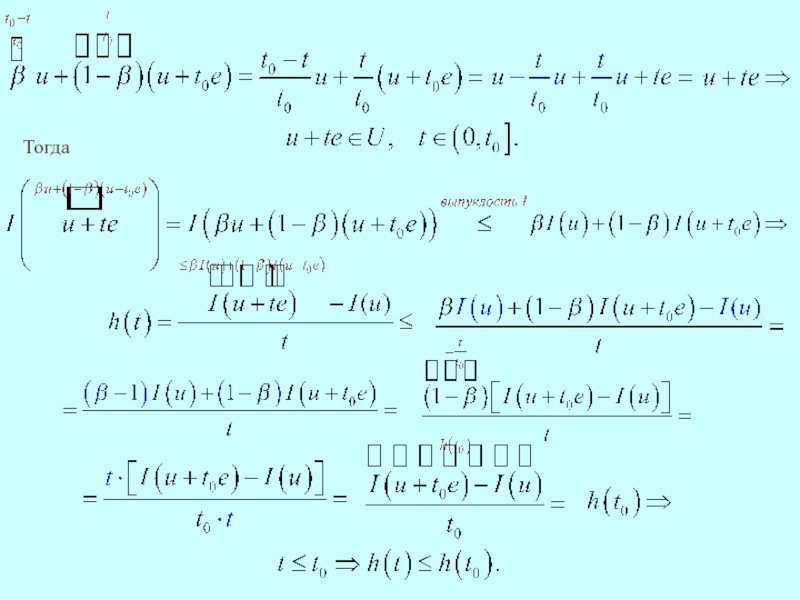- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Выпуклые функции.. Лекция 12 презентация
Содержание
- 1. Выпуклый анализ. Выпуклые функции.. Лекция 12
- 2. 3. ВЫПУКЛЫЕ ФУНКЦИИ (ПРОДОЛЖЕНИЕ)
- 3. 3.3. Непрерывность выпуклой функции.
- 4. Из неравенства (1) следует С другой стороны
- 6. Для граничных точек
- 7. 3.4. Дифференцируемость выпуклой функции
- 8. Пример 7. имеется хотя бы одно
- 9. в
- 11. Тогда Теорема 7. выпукла. Доказательство. Имеет место включение С другой стороны
- 12. Тогда
- 13. Имеет место равенство Тогда
- 15. Упражнение 1. Решение. Функция нормы выпукла и конечна.
3. ВЫПУКЛЫЕ ФУНКЦИИ (ПРОДОЛЖЕНИЕ) 3.4. Дифференцируемость выпуклой функции по всем возможным направлениям. 3.3. Непрерывность выпуклой функции.
Слайд 2
3. ВЫПУКЛЫЕ ФУНКЦИИ
(ПРОДОЛЖЕНИЕ)
3.4. Дифференцируемость выпуклой функции по всем возможным
направлениям.
3.3. Непрерывность
выпуклой функции.
Слайд 3
3.3. Непрерывность выпуклой функции.
оказывается столь сильным,
Теорема 6.
выпукла.
Доказательство.
Сначала предположим, что
с центром в нуле
Неравенство (1.1),
Слайд 5
Общий случай сводится к уже рассмотренному
определенной формулой
Тогда по доказанному она
непрерывна в нуле.
Непрерывной в нуле будет и функция
Эта функция выпукла и для нее выполнено
как сумма непрерывной функции и постоянной.
Теорема доказана.
Слайд 6
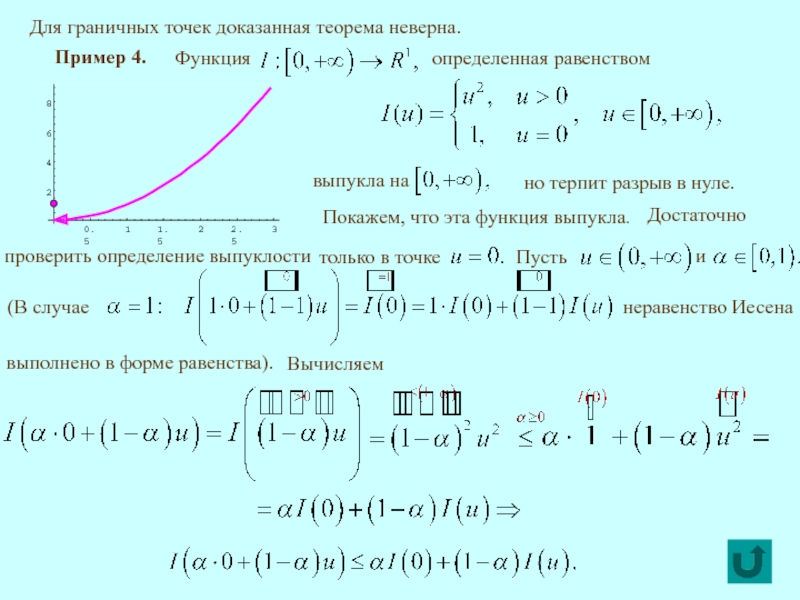
Для граничных точек доказанная теорема неверна.
Пример 4.
но терпит разрыв в
нуле.
Покажем, что эта функция выпукла.
Вычисляем
Слайд 7
3.4. Дифференцируемость выпуклой функции по всем возможным направлениям.
Определение 3.
такое,
что
Пример 5.
Пример 6.
Пусть
Данное включение означает, что
Слайд 8Пример 7.
имеется хотя бы одно возможное направление.
и содержит не
менее двух точек.
Определение 4.
будем называть величину
если этот предел существует.
и дифференцируема в ней,
Слайд 9
в которой она имеет производные по всем направлениям.
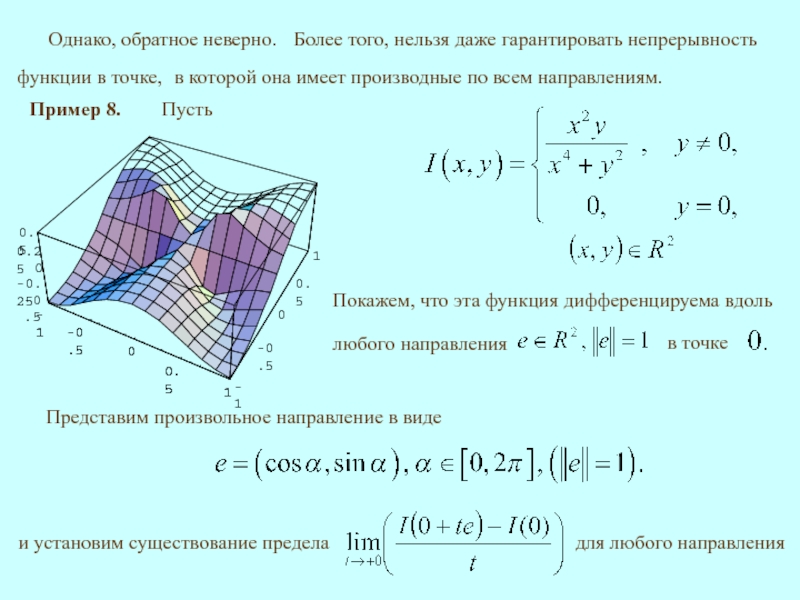
Пример 8.
Пусть
Однако,
обратное неверно.
Представим произвольное направление в виде
и установим существование предела
для любого направления
