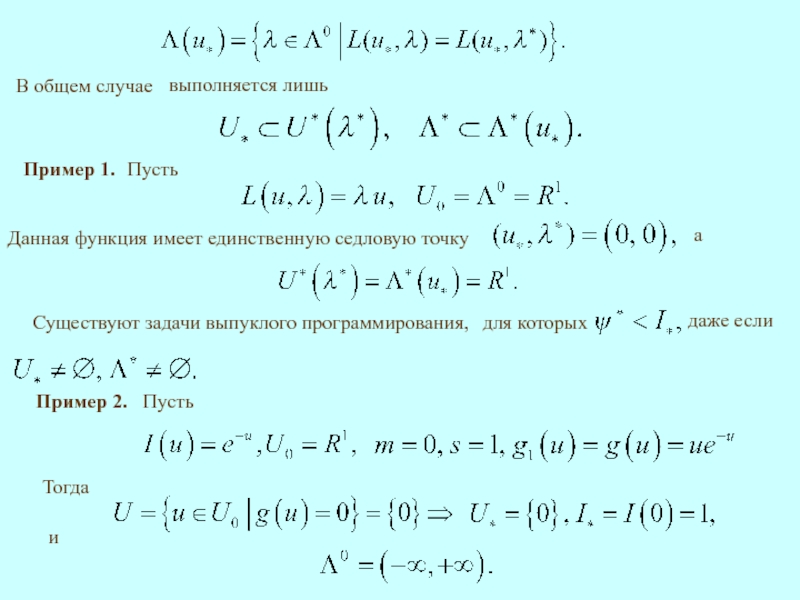- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Теория двойственности. Лекция 27 презентация
Содержание
Слайд 2
10. ТЕОРИЯ ДВОЙСТВЕННОСТИ
10.1. Постановка двойственной задачи.
10.2. Теорема двойственности.
Слайд 3
10.1. Постановка двойственной задачи.
определенную формулой
Нетрудно видеть, что
неравенство переходит
Отсюда выводим равенство
Слайд 4
Тогда исходную задачу можно переписать в виде.
Задача 1.
и сконструируем
Задача 2.
Определение 1.
Задача 2 называется двойственной к задаче 1 (основной).
называются основными,
двойственными.
Слайд 5
10.2. Теорема двойственности.
основной и двойственной задач.
Теорема 1.
Имеет место
Доказательство.
от обеих частей (1)
Обозначим через
множество всех решений двойственной задачи и
Слайд 6
Теорема доказана.
Теорема 2 (двойственности).
Для того чтобы было выполнено
необходимо
Множество седловых точек функции Лагранжа
Доказательство. Необходимость.
Пусть выполнены соотношения (3).
Имеем
Переходя в неравенстве (2)
получим
Слайд 7
Последнее равенство означает, что
Отсюда также следует,
вложено в множество седловых
Достаточность.
седловая точка функции Лагранжа.
Тогда
Отсюда следует
Аналогично из неравенства
Тогда из неравенства (4)
следует, что
Слайд 8
выводим
Из (7),(6)
в силу теоремы 1 получим
Тогда
Отсюда выводим, что множество седловых
Теорема доказана.
Отсюда, в частности следует, что если пары
образуют седловые точки функции Лагранжа,
то и пары
Слайд 9
также являются седловыми точками.
можно выбирать одними и теми же
Тогда
Замечание.
что исходная задача является задачей выпуклого программирования.
Таким образом,
определенная из условия
не обязана быть седловой точкой.
Слайд 10
Пример 1.
Пусть
Данная функция имеет единственную седловую точку
а
Существуют
даже если
Пример 2.
Пусть
Тогда
и
Слайд 11
Выпишем функцию Лагранжа для данной задачи
Вычисляем
Пояснения требует третья строчка
Приведем график функции
Найдем минимизирующую точку
Имеем
Слайд 13
Двойственная задача всегда является задачей выпуклого программирования
какой была основная (исходная)
Действительно, двойственная задача
эквивалентна задаче
Имеем
справедливо