Презентация на тему Выпуклый анализ. Субградиент и субдифференциал функциил. Лекция 19

ВЫПУКЛЫЙ АНАЛИЗ

ЛЕКЦИЯ 19

7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ

(ПРОДОЛЖЕНИЕ)

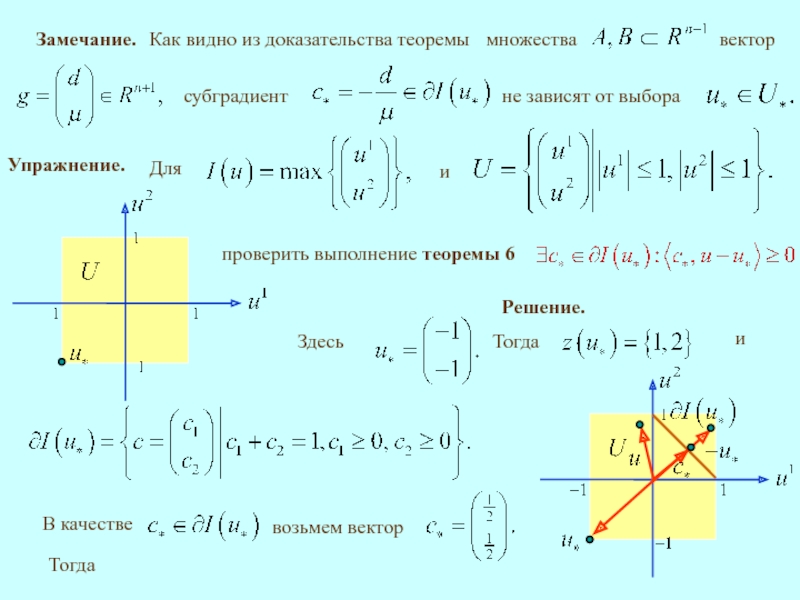
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ (ПРОДОЛЖЕНИЕ)

7.5. Критерий минимума для субдифференцируемых функций.

7.5. Критерий минимума для субдифференцируемых функций.

справедливо следующее утверждение.

Теорема 5.

Доказательство.

Обратно

Для выпуклых функций, определенных на выпуклых множествах,

Теорема 6.

такой, что

Необходимость.

Пусть

Тогда существует гиперплоскость

т.е

Отсюда выводим

Тогда из (1) выводим

перепишем в виде

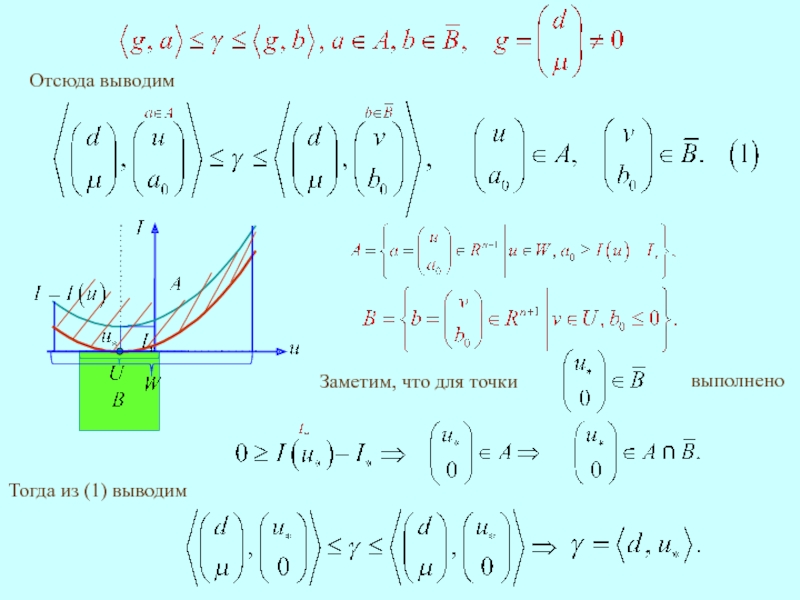
Неравенство (1)

Из правого неравенства в (2) при

получим

Тогда из левого неравенства в (2) выводим

Из (3) выводим

Полагаем в (3)

Разделим (2)

В результате получим

Тогда

Необходимость

доказана.

Достаточность.

По определению субградиента

тогда

Теорема доказана полностью.

Достаточность доказана.

Замечание.

Как видно из доказательства теоремы

Упражнение.

Решение.

Тогда

Следствие.

Действительно,

Пример 4.

не существует.